2种云南松天然次生林林分生长模型构建方法的比较*

陈建珍，何超，许彦红

(1．西南林业大学林业调查规划设计研究院，云南 昆明650224;2．西南林业大学林业3S技术工程研究中心，云南 昆明650224)

云南松 (Pinus yunnanensis)以滇中高原为中心，约分布在北纬 23°～29°，东经 98°30'～106°之间，其中以云南省为最大的分布区［1］。云南松是云南省重要的采脂及用材树种，云南松天然次生林现已成为西南的后续资源，是滇中地区森林经营的主体［2］。天然次生林如果完全处于自然生长状态，不加以科学的经营措施，其年平均生长量则会处于一个相对较低的水平［3］。因此，开展云南松天然次生林林分生长过程研究对于云南省林业的发展具有一定的作用。

不论是天然林还是人工林，在未遭受到严重干扰的情况下，林分内部许多特征因子，如胸径、树高、形数、材积、材种等，都具有一定的分布状态，而且表现出较为稳定的结构规律［4］。准确地预测林分的生长，掌握其生长动态变化规律，是森林经营的一项重要的基础工作。研究森林的生长过程，通常采用建立林分生长模型的方法，揭示森林生长规律，模拟森林的生长过程［5］。林分生长模型通常包括平均胸径生长模型、平均树高生长模型以及蓄积量生长模型。

现有的建模方法主要有3种:机理分析法、测试法和智能建模方法［6］。在林分生长模型建模方法研究上，除根据生物学特征的某些假定条件推导建立的少数模型外，多停留在经验模型阶段，智能建模方法则是一个新兴的研究方向，近年来也逐渐成为研究的一个热点方向［7～8］。在林分生长模型研究中，逐步回归是目前较为理想的筛选自变量的方法［9］;BP网络与传统统计模型相比，其优点在于不需假设函数f(x)的数学结构，只要有足够的隐含层和隐结点，网络就可以逼近任意的非线性映射［10］。BP神经网络建模法已在油松 (Pinus tabulaeformis)［11］、落 叶 松 (Larix gmelinii)［12～13］、杉 木(Cuninghamia lanceolata)［14］等树种的林分生长模型中应用，而在云南松林的生长模型中未见报道。本研究选取了测试法中的逐步回归剔除法和智能建模方法中的BP神经网络建模法，建立云南松天然次生林林分生长模型，并对其预估效果进行比较分析，以期为云南松天然次生林的经营管理提供参考。

1 材料与方法

1.1 材料

本研究实验数据来源于2005年12月-2007年3月野外调查的55块云南松天然次生林标准地。

1.2 调查方法与内容

标准地设置在云南省云南松主要分布区的昆明市、楚雄州，于不同海拔、不同林分密度、不同坡向及坡位、人为干扰少的林分中，具体情况见表1。按照测树学标准地常规调查方法进行林分环境因子及林分测树因子调查［15］。标准地主要林分测树因子统计量见表2。在数据使用前，已对研究数据进行粗差剔除，完成数据的预处理。

表1 云南松天然次生林55块标准地的基本情况Tab．1 Basic situation of 55 sample-plots of Pinus yunnanensis natural secondary forest

1.3 模型建立与泛化力检验

为检验模型的泛化能力［13］，遵循满足基本要求的样本容量原则随机抽取33块标准地数据作为建模数据，余下的22块标准地数据作为模型校验数据［16］。结合相关性分析和利用非样本的先验信息［17］，选定 A、H、SCI、SDI、N，A、Dg、SCI、SDI、N，A、Dg、H、SCI、SDI、G、N，分别作为逐步回归剔除法拟合平均胸径生长模型、平均树高生长模型、蓄积量生长模型的自变量因子。为排除引起多重共线性的自变量并增加两种建模方法的可比性，BP神经网络建模法是在逐步回归剔除部分自变量因子的基础上确定各生长模型的自变量因子。

1.4 数据处理

本研究数据处理均使用MATLAB数学统计软件完成。

表2 云南松天然次生林标准地的主要林分测树因子Tab．2 Statistics of main stand measurement factors of sample-plots

2 结果与分析

2.1 逐步回归剔除法建模

根据逐步回归剔除法原理，选用以下模型进行拟合:K=c1C1+c2C2+c3C3+……+cnCn，式中:K代表林分生长量;c1、c2、c3…cn代表待定参数;C1、C2、C3…Cn代表林分重要测树因子。

设定引入变量的显著性水平P1=0．05、移出变量的显著性水平P2=0．10，使用逐步回归剔除法拟合林分生长模型结果见表3。从表3可知，各生长模型总体拟合精度 (Pc%)在89．22% ～95．52%之间，模型回归相关系数 (R)在0．922 0～0．960 4之间，拟合效果均较好。

表3 逐步回归剔除法拟合的最终云南松天然次生林林分生长模型Tab．3 Stand growth models of Pinus yunnanensis natural secondary forest established by stepwise regression

2.2 BP神经网络建模

根据BP网络模型的映射原理，对输入样本集合X和输出Y，假设其存在一映射:Yi=F(Xi)，(i=1，2，…，n)，其中n为样本数。

表4 BP神经网络建模法拟合的云南松天然次生林林分生长模型Tab．4 Stand growth model of Pinus yunnanensis natural secondary forest established by BP neural network

设模型性能函数为均方误差 (MSE，Mean Square Error)，经过反复多次训练比较，得出最佳林分生长模型，其中各生长模型及其主要训练参数值和模型评价指标见表4，各模型训练结束后的权值和阈值见表5～表7。从表4可知，各生长模型Pc%在90．01% ～98．62%之间，R 在 0．970 3 ～0．998 1之间，拟合效果均好。

表5 平均胸径生长模型训练结束后的权值和阈值Tab．5 Weight and threshold after average DBH growth model training

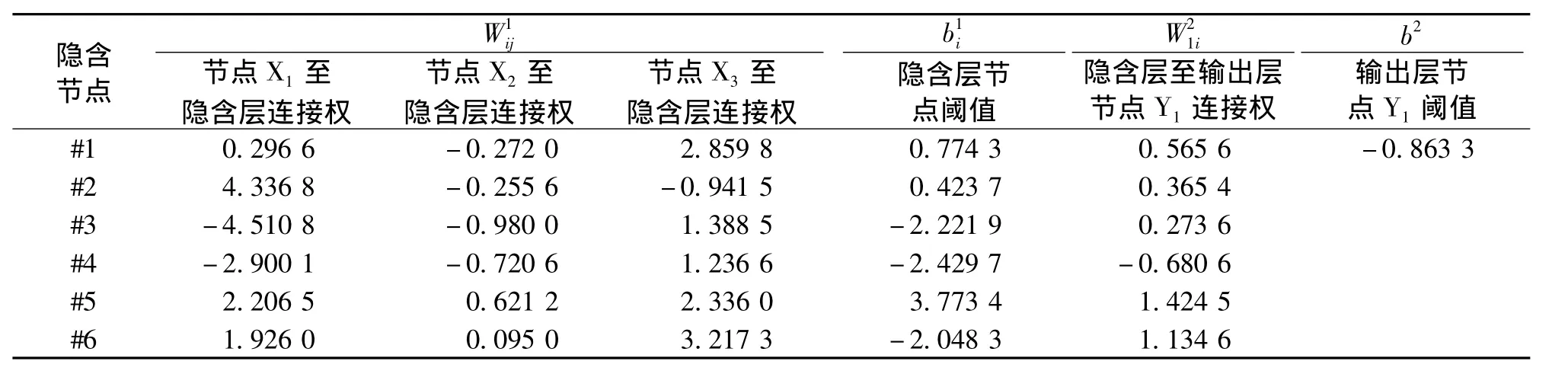
表6 平均树高生长模型训练结束后的权值和阈值Tab．6 Weight and threshold after average height growth model training

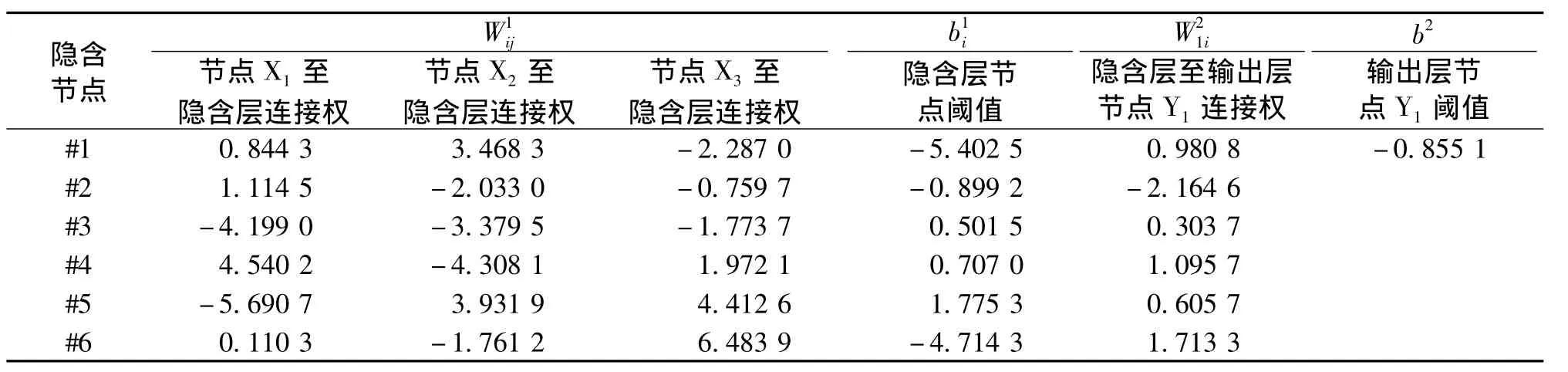
表7 蓄积量生长模型训练结束后的权值和阈值Tab．7 Weight and threshold after average volume growth model training

2.3 模型泛化力检验及比较

本研究采用独立有效性检验方法对拟合出来的平均胸径生长模型、平均树高生长模型、蓄积量生长模型进行泛化力检验，即是将用于模型校验的22块标准地实测的云南松林分各测树因子作为实际值，用33块标准地建立的生长模型所预估的22块标准地云南松林分各测树因子作为理论值进行模型分析。结果见表8。

经回归分析得出用逐步回归剔除法建立的模型R在0．860 2～0．972 7之间，用BP神经网络建立的模型R在0．951 1～0．980 5之间，可见两种方法建立的模型拟合、预测输出结果与实测值具有很高的相关性，说明所建立的生长模型拟合效果较好。

经拟合精度分析得出用逐步回归剔除法建立的模型Pc%在81．09% ～94．15%之间，用BP网络建立的模型Pc%在92．63% ～95．68%之间，可见理论值与实际值吻合很好，符合检验精度的要求［18］。

表8 各生长模型检验指标Tab．8 Test indicators of each growth model

综合平均误差绝对值 (MAE，mean absolute error)、MSE、Pc%、R等各项指标得出BP网络模型的预估效果更佳，误差更小，模型适应性更强，模型可为云南松天然次生林的森林经营管理提供参考。

3 结论与讨论

在55块云南松天然次生林标准地样本中随机抽取33块标准地数据作为建模数据，余下的22块标准地数据作为模型校验数据，使用逐步回归剔除法及BP神经网络技术建立林分生长模型。

模型拟合精度检验结果:使用逐步回归剔除法建立的各生长模型Pc%在89．22% ～95．52%之间，R在0．922 0～0．960 4之间;使用BP神经网络技术建立的各林分生长模型Pc%在90．01% ～98．62%之间，R 在0．970 3 ～0．998 1 之间，说明拟合效果均较好。

模型泛化力检验结果:使用逐步回归剔除法建立的各生长模型Pc%在81．09% ～94．15%之间，R在0．860 2～0．972 7之间;用BP网络建立的模型Pc%在92．63% ～95．68%之间，R 在0．951 1～0．980 5之间，检验效果理想。

通过研究比较得出，在研究区内云南松天然次生林林分的生长模型构建中BP神经网络建模拟合精度比逐步回归剔除法建模拟合精度高出0．79%～4．19%，检验精度则高出 1．53% ～11．54%，说明其所建立模型精度比逐步回归剔除法的高，泛化效果更强，模型可为同类森林的经营管理提供参考。因为非线性、复杂性是林分生长系统的本质特征，而BP网络在非线性建模方面具有明显的优势，它能对任意非线性映射进行任意逼近，故能比常规建模方法更能精确地模拟现实林分生长系统。

虽然本研究所建立的模型精度比大部分其他已经发表的云南松林分生长模型的精度高，但因为建模所用数据并不相同，可能会存在一定的差异，在今后的研究中有待进一步研究。

［1］郑万钧．中国树木志(第一卷)［M］．北京:中国林业出版社，1983．

［2］云南省林业厅．云南松［M］．昆明:云南科技出版社，2004．

［3］胥辉．思茅松天然次生林林分生长模型的研究［J］．云南林业科技，2001(2):13-16．

［4］舒娱琴．基于林分生长规律的虚拟森林环境的构建研究［D］．武汉:武汉大学，2004．

［5］唐守正，李希菲，孟昭和．林分生长模型研究的进展［J］．林业科学研究，1993，6(6):672-679．

［6］薛晓东．建模方法综述［J］．科技情报开发与经济，2009，19(16):169-171．

［7］Guan B T，Gertner G．Using a parallel distributed processing system to model individual tree mortality［J］．Forest Science，1991，37:871-855．

［8］Susan L King，Kristin P Bennett，Shannon List．Modeling noncatastrophic individual tree mortality using logistic regression，neural networks，and support vector methods［J］．Computers and Electronics in Aagriculture，2000，27(1-3):401-406．

［9］胥辉，张会儒．林木生长量模型研究［M］．昆明:云南科技出版社，2002．

［10］高光芹，郭芳，黄家荣．用人工神经网络构建多形地位指数模型［J］．西部林业科学，2014，43(4):101-105．

［11］徐步强，张秋良，弥宏卓，等．基于BP神经网络的油松人工林生长模型［J］．东北林业大学学报，2011，39(12):33-35．

［12］阚龙攀，黄家荣，赵俊卉，等．基于BP神经网络的落叶松生长模型研究［J］．江苏农业科学，2010(1):366-367，379．

［13］金星姬，贾炜玮，李凤日．基于BP人工神经网络的兴安落叶松天然林全林分生长模型的研究［J］．植物研究，2008，28(3):370-374，384．

［14］易娟．基于神经网络的杉木人工林全林分模型［D］．福州:福建农林大学，2009．

［15］孟宪宇．测树学(第3版)［M］．北京:中国林业出版社，2006．

［16］耿修林．社会调查中样本容量的确定［M］．北京:科学出版社，2008．

［17］张雄清，张建国，段爱国．基于贝叶斯法估计杉木人工林树高生长模型［J］．林业科学，2014，50(3):69-75．

［18］杨潇，张秋良．基于BP人工神经网络的大青山自然保护区华北落叶松人工林全林分生长模型研究［J］．内蒙古农业大学学报，2012，33(5-6):76-79．