基于Geo-Studio软件的超细粒尾矿子坝堆筑可靠度分析

唐 恺 唐开波 孙宜耐

(1.中钢集团马鞍山矿山研究院有限公司；2.金属矿山安全与健康国家重点实验室；3.华唯金属矿产资源高效循环利用国家工程研究中心有限公司；4.淮北四铺中联水泥有限公司；5.山东黄金矿业(玲珑)有限公司)

基于Geo-Studio软件的超细粒尾矿子坝堆筑可靠度分析

唐 恺1,2，3唐开波4孙宜耐5

(1.中钢集团马鞍山矿山研究院有限公司；2.金属矿山安全与健康国家重点实验室；3.华唯金属矿产资源高效循环利用国家工程研究中心有限公司；4.淮北四铺中联水泥有限公司；5.山东黄金矿业(玲珑)有限公司)

基于Geo-Studio软件Slope模块建立超细粒尾矿后期子坝加高堆筑模型，摒弃了传统定值法(安全系数法)在尾矿坝设计和稳定性评价中的不足，运用Monte-Carlo模拟法对子坝后期加高进行了可靠度分析，分别计算了坝体加高10，20 m，在正常工况、洪水工况和特殊工况下的失效概率和可靠度指标，更加全面、客观地反应后期子坝加高坝体稳定性的真实状态。

超细粒尾矿 子坝堆筑 Monte-Carlo 失效概率 可靠度

尾矿坝坝坡稳定问题一直是尾矿坝设计和运行过程中一项重要的研究内容。传统的稳定性分析方法都是把诸多因素看作定值，而在实际运行过程中存在大量的不确定因素，定值法并不能完全反应出来，无法对尾矿坝体实际的稳定状态作出准确评价。

对于尾矿坝工程设计和评价人员来说，在诸多不确定因素中尤以计算参数的空间变异性最为重要。首先是岩土性质本身在空间和时间域上的可变性，其次是室内或现场土工试验本身也存在各种试验误差，土工试验组数不可能太多，从统计意义上讲，样本数量并不能完全满足要求，直接使用这些试验结果，往往会获得不完全反映实际情况的变异系数。本文以云南省安宁市某超细粒尾矿后期子坝加高为例，利用Geo-Studio软件Slope模块，将岩土计算参数变化对尾矿坝稳定性的影响进行了可靠度计算和分析，得出更为真实的尾矿坝稳定情况，以确保尾矿坝安全。

目前国内对尾矿坝可靠度分析方面的研究甚少，尤其是运用超细粒尾矿加坝可靠性的研究更少。胡平安、韩森采用JC法作为可靠度分析方法，求出了尾矿坝在正常工况和洪水工况下运行时的可靠度指标[1]。郑荣跃、梧松考虑计算模型的不确定性，并在此基础上提出了一种改进的边坡可靠度分析方法[2]。李国政、李培良、徐宏达对比水利、水电永久标准，给出了尾矿库坝体堆积至510～520 m标高时稳定性及结构可靠度分析参数[3]。

1 概 述

由于尾矿坝边坡工程的一系列基本设计变量的不确定性，分析方法不足以评价不确定性因素对工程设计影响，而可靠性理论恰恰可以提供解决该方面问题的手段。可靠性分析方法与其他传统的稳定性分析一样，其关键步骤是寻找一个合适的数学模型，即以函数的形式定义边坡的状态方程：

Z=g(X)=g(x1,x2,…,xn) ，

(1)

式中，X为基本随机向量。

如果工程问题比较简单，函数Z的形式则比较明确，且容易确定；对于复杂的边坡工程，需要进行精确求解，因为在安全系数计算模型中往往包含隐函数。然而，不管函数Z多么复杂，其可靠性分析的原理是相同的，只要基本随机变量是不随时间变化的参数，那么其可靠度：

R=1-Pf

(2)

式中，fx1,x2,…，xn(x1,x2,…,xn)为n个变量xi的联合概率密度函数。

显然，这里存在两个实际问题：①很难有充足的数据来确定n个基本变量的联合概率密度函数，也很难有充足的数据来保证边缘分布函数和协方差是可信的；②即使联合概率密度函数或式(2)中的边缘密度函数是已知的，多维积分也难以实现。对于大多数实际问题不存在解析解，必须求助于其他计算方法来计算可靠度指标。

2 可靠性分析计算方法

目前可靠性分析计算方法有4种:可靠度指标法、统计矩法、随机有限元法和蒙特卡罗(Monte-carlo)模拟法[4-5]。

蒙特卡罗模拟法是依据统计抽样理论，利用计算机研究随机变量计算可靠性，是相对精确的数值计算方法。其基本步骤是：首先产生一系列均匀随机数，然后根据各随机变量所服从的随机分布规律随机抽取一组随机数，以这些随机数计算极限状态函数值，重复N次，作出安全系数或安全余量的分布图，统计出均值以及F≤1或Z≤0的样本数，求得可靠度指标β和破坏概率Pf[6]。

在模拟评价尾矿坝边坡可靠度时，蒙特卡罗(Monte-carlo)模拟法有以下优点：①受问题条件限制的影响小，其收敛性与极限状态函数的非线性、变量分布的非正态性无关;②对于适用于边坡破坏模式的任何极限平衡分析方法，只要知道状态变量的概率分布，均可求解，适用性强;③对于变异系数大于30%的情况，其他方法的可靠度计算结果可能与精确解相差甚远，而蒙特卡罗(Monte-carlo)模拟法不受这个约束。

选择蒙特卡罗模拟法作为本项分析的可靠性计算方法。

3 可靠性分析

3.1 许可破坏概率和可靠度指标

破坏概率就是安全系数小于1.0的概率，即安全系数小于1的取样试验计算所得安全系数的次数和总的Monte-Carlo试验次数比值的百分数。

可靠度指标是评估边坡不稳定性的另外一种方法，是通过安全系数的平均值偏离已定义失稳值1.0标准差的次数来评价的。

水工建筑物级别及结构安全级别具有对应关系，具体见表1。

表1 水工建筑物结构安全级别

尾矿库加高后属于三等尾矿库，水工建筑物级别属于3级，由表1可知，水工建筑物结构安全级别属于Ⅱ级。根据《水利水电工程结构可靠度设计统一标准》(GB50199-94)，对各结构安全级别的许可可靠度指标作了规定，参照表2。本次研究可靠性分析按照二类破坏，采用的许可安全可靠度指标为3.7。

表2 水利、水电永久工程可靠度指标

3.2 计算参数

根据土工试验研究数据统计分析，得出可靠性分析参数，见表3。

表3 可靠性计算参数

3.3 计算结果

本次计算主要寻求超细粒尾矿后期子坝加高10,20 m的可能性及加高后尾矿坝的稳定性。首先计算坝体加高10 m后，在正常工况、洪水工况和特殊工况下的可靠度指标，若满足要求，坝体可以加高10 m；若不满足要求，通过增设排渗措施，对坝体浸润线调整后再计算可靠度指标。若满足要求，表明坝体可以加高10 m，反之利用超细粒尾矿子坝体加高10 m不可靠。

同理，计算坝体加高20 m后在正常工况、洪水工况和特殊工况下的可靠度指标。

细粒尾矿堆积坝可靠性计算结果如表4和图1～图8。

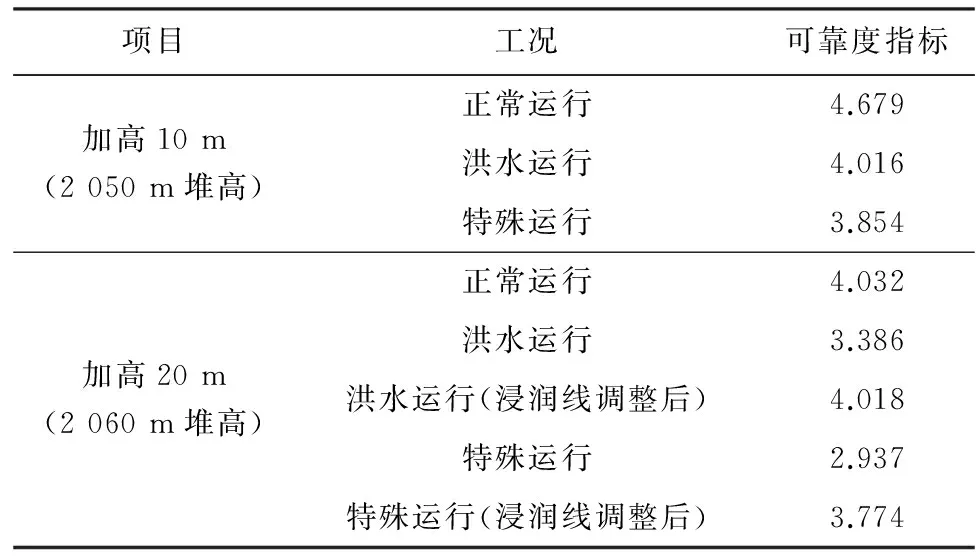
表4 可靠性计算结果

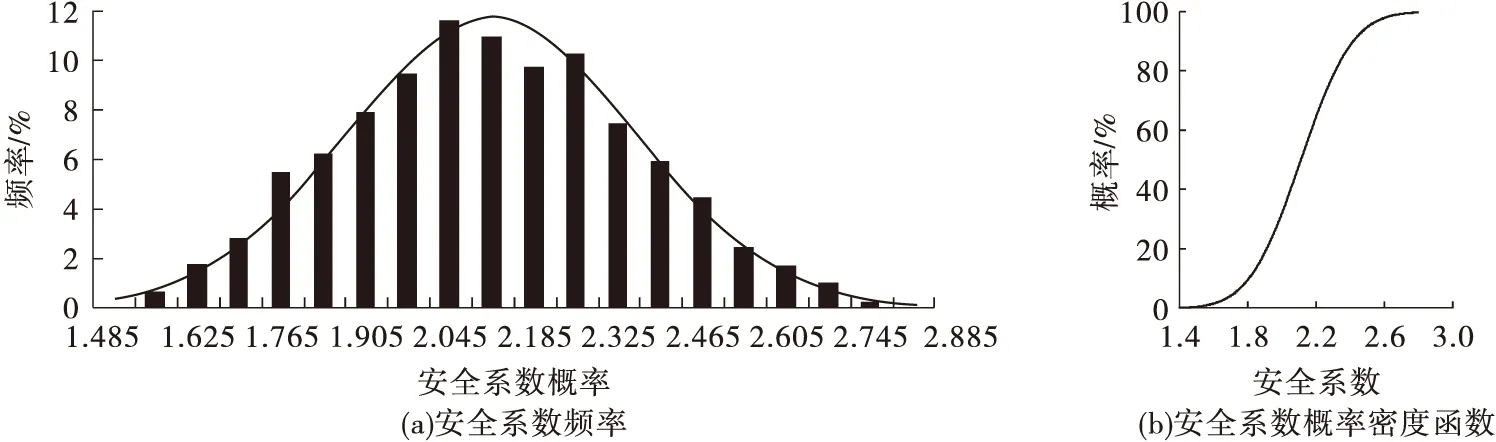
图1 尾矿堆积坝加高10 m(2 050 m堆高)正常运行安全系数概率密度函数

图2 尾矿堆积坝加高10 m(2 050 m堆高)洪水运行安全系数概率密度函数

图3 尾矿堆积坝加高10 m(2 050 m堆高)特殊运行安全系数概率密度函数

根据表4、图1～图8,参照水利、水电永久工程可靠度指标表2，可以得出：

(1)坝体加高10 m时，细粒尾矿堆积坝在正常工况、洪水工况和特殊工况下的可靠度指标均大于3.7，高于Ⅱ级，符合规范要求。

(2)坝体加高20 m时，细粒尾矿堆积坝在正常工况的可靠度指标为4.032，大于3.7，高于Ⅱ级；在洪水工况和特殊工况下的可靠度指标分别为3.386和2.937，小于3.7，不能够满足规范要求。对坝体加高20m浸润线调整后的尾矿堆积坝重新进行可靠度计算，结果表明浸润线调整后的尾矿堆积坝在洪水工况下运行的可靠度指标由3.386增大到4.018，在特殊工况下运行的可靠度指标由2.937增大到3.774，均能够满足规范要求。

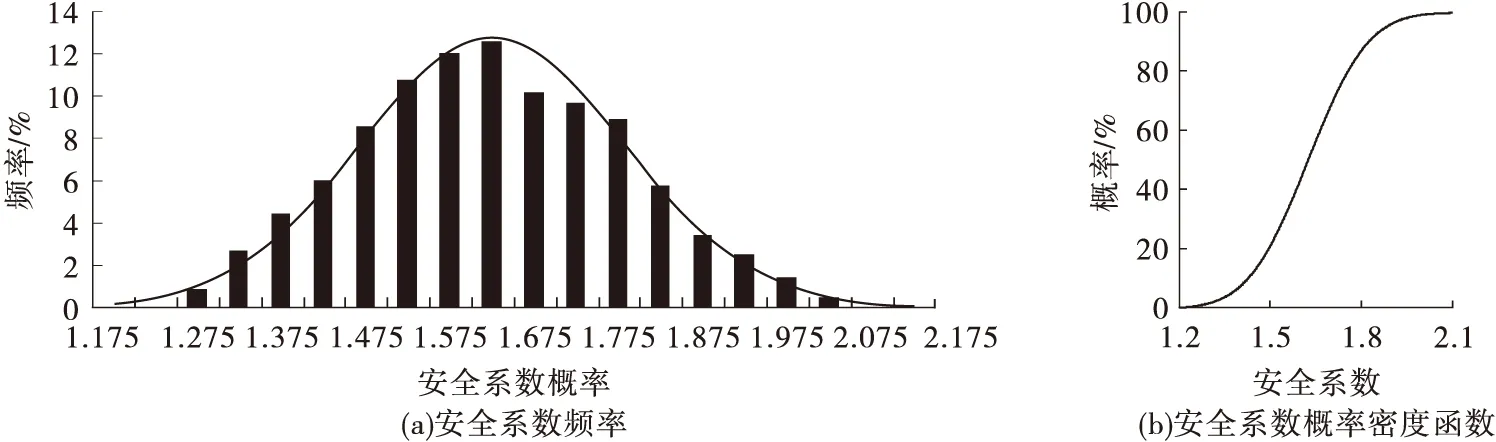
图4 尾矿堆积坝加高20 m(2 060 m堆高)正常运行安全系数概率密度函数

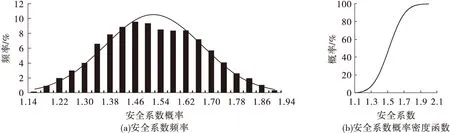
图5 尾矿堆积坝加高20 m(2 060 m堆高)洪水运行安全系数概率密度函数

图6 尾矿堆积坝加高20 m(2 060 m堆高)浸润线调整后洪水运行安全系数概率密度函数

图7 尾矿堆积坝加高20 m(2 060 m堆高)特殊运行安全系数概率密度函数

图8 尾矿堆积坝加高20 m(2 060 m堆高)浸润线调整后特殊运行安全系数概率密度函数

4 结 语

(1)运用Geo-Studio软件Slope模块，对超细粒尾矿后期子坝加高进行了可靠性分析，对由于计算参数的变异性给稳定性分析造成的影响，采用Monte-Carlo法求出了坝体加高10，20 m在正常工矿、洪水工况和特殊工况下的失效概率和可靠度指标，弥补了定值法(安全系数法)在尾矿坝设计和稳定性评价中的不足，使坝体稳定性分析更加符合工程实际，准确科学。

(2)根据计算结果，随着细粒尾矿筑坝高度的增加，尾矿坝的可靠度指标不断降低，在细粒尾矿筑坝20 m高度的洪水工况和地震工况运行时，尾矿筑坝自身的可靠度指标降低到3.386和2.937，已不能满足规范要求；细粒尾矿筑坝10 m高度和经过加固后20 m高度的地震工况运行时，尾矿筑坝自身的可靠度指标分别为3.854和3.774，余量不大。

(3)由计算结果可知，浸润线高度对细粒尾矿坝自身的可靠度指标有较大影响，通过在坝体中增设排渗设施降低浸润线，对尾矿坝重新进行可靠性计算，结果能够满足规范要求。

(4)通过对尾矿坝加高10，20 m两种情况进行的结构可靠度分析，准确得出坝体的可靠级别，细粒尾矿堆积坝在加高10 m时，为Ⅱ级以上的可靠级别；加高20 m时，增设排渗措施、降低浸润线后的可靠度也可达到Ⅱ级以上的可靠级别。

[1] 胡平安，韩 森.基于JC法尾矿坝稳定性可靠度研究[J].中国安全生产科学技术，2010(4)：56-59.

[2] 荣 跃，梧 松.基于Spencer法的边坡稳定性可靠度指标分析[J].岩土力学，2006(1)：147-150.

[3] 李国政，李培良，徐宏达.基于结构可靠度指标的尾矿库坝体稳定性分析[J].黄金， 2005(6)：48-50.

[4] 马鞍山矿山研究院.边坡可靠性研究与优化决策[R]．马鞍山：马鞍山矿山研究院，2000．

[5] 祝玉学.边坡可靠性分析[M].北京：冶金工业出版社，1993.

[6] 赛义德.可靠性工程[M].杨 舟，译.北京：电子工业出版社，2013.

Reliability Analysis of Ultra Fine Grained Tailings Dam Based on Geo-Studio Software

Tang Kai1,2,3Tang Kaibo4Sun Yinai5

(1. Sinosteel Maanshan Institute of Mining Research Co.,Ltd.； 2. State Key Laboratory of Safety and Health for Metal Mine； 3. Huawei National Engineering Research Center of High Efficient Cyclic and Utilization of Metallic Mineral Resources Co.,Ltd.; 4. Huaibei Sipu China United Cemen Corporationt; 5. Shandong Gold Mining(Linglong)Limited Co.,Ltd.)

The late sub-dam heightening heap up model of the ultra fine grained tailings dam is established based the studio module of Geo-Slope software,so,the shortcomings of the traditional fixed value method(coefficient of safety method) in evaluation of design and stability of tailings dam is abandoned.The Monte-Carlo simulation method is used to conduct reliability analysis on the late sub-dam heightening.The failure probabilities and reliability indexs of the sub-dam heightening 10 m and 20 m under normal conditon,flood condition and the special condition are calculated separately so as to response the actual stability state of the late sub-dam heightening more comprehensively and objectively.

Ultra fine grained tailings, Sub-dam stacking, Monte-Carlo, Failure probability, Reliability

2015-05-10)

唐 恺(1985—)，男，硕士，243000 安徽省马鞍山市经济技术开发区西塘路666号。