数学建模在中学教学中的应用

温州技师学院 缪海芬

数学建模在中学教学中的应用

温州技师学院 缪海芬

数学建模回应了教育界提出的“以问题为纽带的教学”这一教育新理念，学习数学建模顺应了当前教学改革的需要。中学阶段，数学建模是贯穿整个数学课程的重要内容，渗透在每个模块或专题中。本文采用建立相关初等数学模型的建模方法，以若干个初等数学模型为例，介绍初等数学模型的组建及应用，以期为中学数学建模教学提供参考。

数学模型 函数模型 不等式模型 数列模型

一、引言

数学模型是架于数学理论和实际问题之间的桥梁，它是解决问题的常用方法，常用来解决一些实际问题。它要求学生把实际问题转化为一些具体的数学问题，从而使问题获得解决。中学教材重视数学建模与应用，主要体现在数学建模作为问题解决的重要工具之一．中学阶段，数学建模是贯穿整个数学课程的重要内容，渗透在每个模块或专题中。本文以若干个初等数学模型为例，介绍初等数学模型的组建及应用，以期为中学数学建模教学提供参考。

二、中学数学建模举例

中学数学建模的模型常见的主要有函数模型、不等式模型、方程模型。

1.函数模型

用函数的观点解决实际问题是中学数学中最重要、最常用的方法。两个变量或几个变量，凡能找到它们之间的联系，并用数学形式表示出来，建立起一个函数关系（数学模型），然后运用函数的有关知识去解决实际问题，这些都属于函数模型的范畴。

案例1：函数的应用举例

以下是某地区不同身高的未成年男性的体重平均值表：

身高/cm 60 70 80 90 100 110 120 130 140 150 160 170体重/kg 6．13 7．90 9．99 12．15 15．0217．50 20．92 26．86 31．11 38．85 47．25 55．05

根据表中的数据，建立该地区未成年男性体重与身高的函数模型，并分析和讨论。规定体重超过相同身高男性平均值的1.2倍为偏胖，低于0.8倍为偏瘦，问该地区某中学一男生身高为175cm，体重为78kg，他的体重是否正常？

Step1.模型假设

（1）该地区未成年人人数固定。

（2）假设体重只与身高相关，忽略其他一切因素。

Step2.建立模型

用计算机拟合表中数据，画出散点图（图1）：

根据散点图的形状判断，我们猜测在该地区，体重与身高的关系为y=a•bx。

Step3.求模型参数

任选两组数据代入y=a•bx，近似求出参数a,b，所选式子的待定常数的值。

例如，选数据x=70,y=7.90和x=160,y=47.25，代入

所以，该地区未成年男性体重关于身高的近似函数关系式可选为y=2×1.02x。

Step4.检验

将已知数据代入所得函数解析式，或作出所得函数的图象（图2），可知所求函数能较好地反映该地区未成年男性体重与身高的关系。

把表中数据代入函数y=2×1.02x，检验函数值是否与已知体重数据基本吻合。

Step5.模型的改进

为了使所求得的参数a,b的值更精确，可采用参数估计法，例如线性回归模型求参数，并进行各种检验或残差分析等。

2.不等式模型

在现实生活中，存在着大量的不等关系，例如投资决策、生产规划、追求利润、人口控制、环境保护、交通运输等问题的求解过程，都可归结为不等关系的论证与求解。利用不等式知识解决实际问题，将实际问题中的一些变量如何对应转化到这些模型中去，是解决问题的关键。

案例2： 饮料罐制造用材问题

问题：怎样使饮料罐制造用材最省？

模型假设：

（1）把饮料罐假设为圆柱体。

（2）假设用金属（如铝材）制造饮料罐，并设其厚度为b。

（3）设饮料罐各部分厚度均匀，即饮料罐上、下底和侧面的厚度相同。

（4）制造中不考虑折边（焊接）长度。

引入参数：罐装饮料的体积为V，半径为r，圆柱高为h，制罐用材的总面积为A。

模型建立和求解：

制罐用材的总面积A，即A=(2πr2＋2πrh)b。

讨论和改进：由上知，罐高h为半径r的2倍，即罐高与直径相等时，饮料罐制造用材最省。事实上，测量几家著名的饮料如可口可乐、百事可乐、健力宝等饮料罐后，发现其高和半径的比约为4：1。难道它们都没发现h:r=2:1时，用材最省吗？查阅相关资料后，得知由于饮料罐上底的厚度比罐的其它部分厚，一般厚三倍左右。因此，假设（3）进一步改为“饮料罐上底的厚度为3b, 其它部分为b”。

3.方程模型

霍金曾说，科学家和工程师喜欢用方程的形式表达他们的思想，因为方程是描述数学思想简明而精确的方法和手段，有了方程就能够得到数量的准确值。

案例1 ：“锤子、剪刀、布”

问题背景：约定：“布”赢“锤子”得9分，“锤子”赢“剪刀”得5分，“剪刀”赢“布”得2分。小明和某同学玩游戏过程中，小明赢了21次，得108分。列出各种可能的赢法。

分析：这是一个简单的一次不定方程,由初中二元一次方程组的应用题改编而成。

Step1.问题假设

①假设约定：“布”赢“锤子”得9分，“锤子”赢“剪刀”得5分，“剪刀”赢“布”得2分。

②假设“小明赢了21次，得108分”符合客观事实。

Step2.模型建立

设“布”赢“锤子” 为x次，“锤子”赢“剪刀”为y次,“剪刀”赢“布”为z次, （x,y,z均为正整数）。

由问题得不定方程

Step3.模型求解

方程⑴有若干组正整数解，利用maple语句：

＞ for z from 0 to 21 do

isolve({x+y+z=21,9*x+5*y+2*z=108});

od;

很容易求得解为：

{x=3,y=15,z=3},{x=6,y=8,z=7},{x=9,y=1,z=11}

Step4.小结

本题中，小明赢了21次，得108分，共有三种赢法，列表如下：

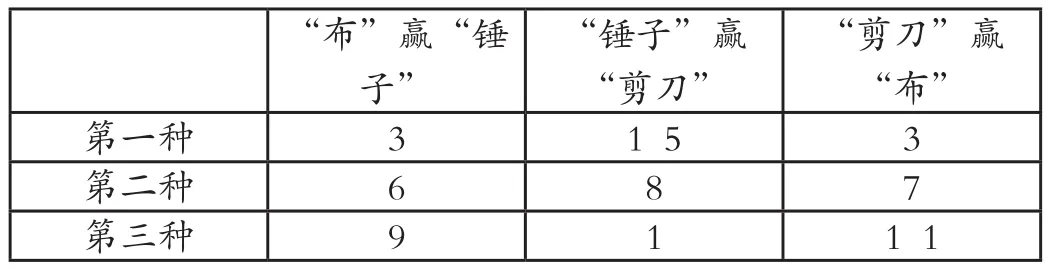
“剪刀”赢“布”第一种 3 15 3第二种 6 8 7第三种 9 1 11“布”赢“锤子”“锤子”赢“剪刀”

Step5.讨论

在不考虑客观事实下，即将赢的次数或总得分任意更改，则所有的可能赢法会相应改变，例如：

①将“21次、108分”改为 “21次、142分”，则有两种赢法：

｛x=10,y=10,z=1｝,{x=13,y=3,z=5}；②将“21次、108分”改为 “21次、45分”，则有一种赢法：｛x=0,y=1,z=20｝；③将“21次、108分”改为 “21次、32分”，则无解。如果更改假设①的约定，则赢法种类又会相应变化。利用maple编程很容易得到。

三、结论和讨论

数学建模能帮助我们独辟蹊径，简洁有效地解决一些实际问题。在数学教学过程中，要选择具有关键作用的变量及相应的数学工具，从而使复杂问题简单化，具体问题抽象化。最后将实际数据代人数学模型，即模型的应用。在高中阶段，教材非常重视数学建模与应用,数学建模是贯穿整个数学课程的重要内容，并渗透在每个模块或专题中，在教学中不断进行研究性学习，并不断加以完善，以发展的眼光丰富中学数学建模的内容。

[1]姜启源．数学模型（第二版）[M]．北京:高等教育出版社，1998

[2]刘来福，曾文艺．数学模型与数学建模[M]．北京:北京师范大学出版社，1998

[3]黄忠裕．初等数学建模[M]．成都:四川大学出版社，2004

[4]人民教育出版社中学数学室．全日制普通高级中学教科书（必修）数学第一册（上）[M]．北京:人民教育出版社，2003

ISSN2095-6711/Z01-2015-08-0191