基于组合证据冲突修正的凝汽器真空度多网络融合预测

夏琳琳 台金娟 文 磊

(东北电力大学自动化工程学院，吉林 吉林 132012)

凝汽器是一种多管束换热器[1,2]，真空度是凝汽器的一个重要指标，为保证机组安全、经济运行，用户需掌握真空度定量值，确保其工作在最佳运行方式。真空度本身不易测量，应试图找到辅助变量与主导变量(真空度)之间的变化规律，即可实现间接指标的反馈控制。由于机理分析的复杂性，更适合采用人工神经网络(Artificial Neural Network，ANN)去学习、发现变量之间的确切关系，即实现预测。就预测问题而言，组合预测(如多网络融合预测)模式比单一预测更系统，可有效避免单一模型受某些环境随机因素的影响，提高真空度预测的精度[3]。

笔者根据凝汽器运行特性，借助核主成分分析(Kernel Principal Component Analysis，KPCA)方法，构造了五辅助变量的5-n-1结构ANN软测量模型，分别选取BP、RBF、Elman 3个前馈网络进行单一预测，为后续模糊软集与D-S证据理论下的组合预测提供依据。通常，在组合证据完全或严重冲突的情况下，D-S合成公式会因此失效，造成与实际情况不相符。笔者在已取得成果(文献[4])的在线参考模型下(表征冲突程度的k值偏大)，继续利用证据冲突模式下的基本概率再分配方法，修正模糊软集提取下的权重系数，提高预测的精准度。

设Bel1和Bel2是同一识别框架Θ上的两个信任函数，m1和m2分别是其对应的基本概率数，其正交和存在，对应的焦元分别为B1,B2,…,Bk和C1,C2,…,Cr，则Dempster组合规则定义为：

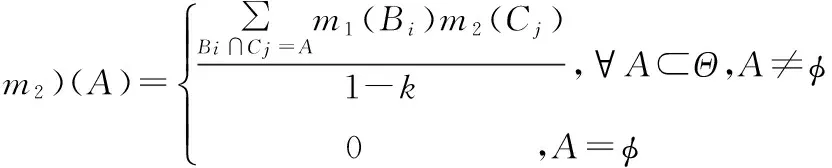
(1)

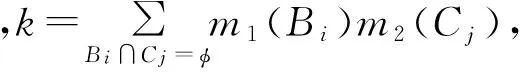
当出现k→1的情况，若能够通过修改组合证据间的权重系数，即改变实际证据的重要程度，且确保冲突程度较大的证据对合成结果的影响较小，即可实现对式(1)所示模型的修正，保证数据融合仍可在Dempster组合预测框架下进行。具体步骤如下：

a. 假设n个不同的证据源在同时提供证据，令证据集E={E1，E2，…，En}，则待确定的权重向量可表示为W={w1,w2,…,wn}；

b. 计算E集中证据Ei与其他证据Ej的冲突程度Kij，构成证据Ei的冲突向量；

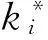
d. 计算kiN的熵值Hi和熵值的倒数Hi-1=1/Hi；

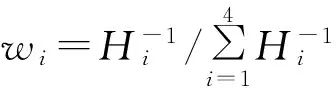
f. 由公式w*=w/wmax，计算证据的“折扣率”，用以调整辨识框架内的基本概率分配值，构造基本概率分配函数；

g. 将上述结果代入新的合成公式，计算多重融合下证据的基本概率数和k值，评价冲突程度对预测结果的影响。

2 融合多网络的真空度预测

网络模型的建立需进行数据预处理以确定输入神经元，多网络融合需离线提取权值，多重数据融合需Dempster组合规则构造模型，组合证据出现冲突需进行修正和权值再分配，以下以某电厂连续4天实测的现场参数构成样本空间，给出详尽的设计过程[5,6]。数据预处理借助文献[4]的研究成果，此处不做赘述。

2.1 单一神经网络预测模型

ANN作为通用的非线性逼近器，可以逼近任意的非线性映射关系。将凝汽器真空度作为主导变量，图1所示的5个主成分作为辅助变量，以三层网络为例，构造单一网络预测的软测量模型(图1)，分别选取BP、RBF、Elman 3种典型网络进行样本的训练和预测。

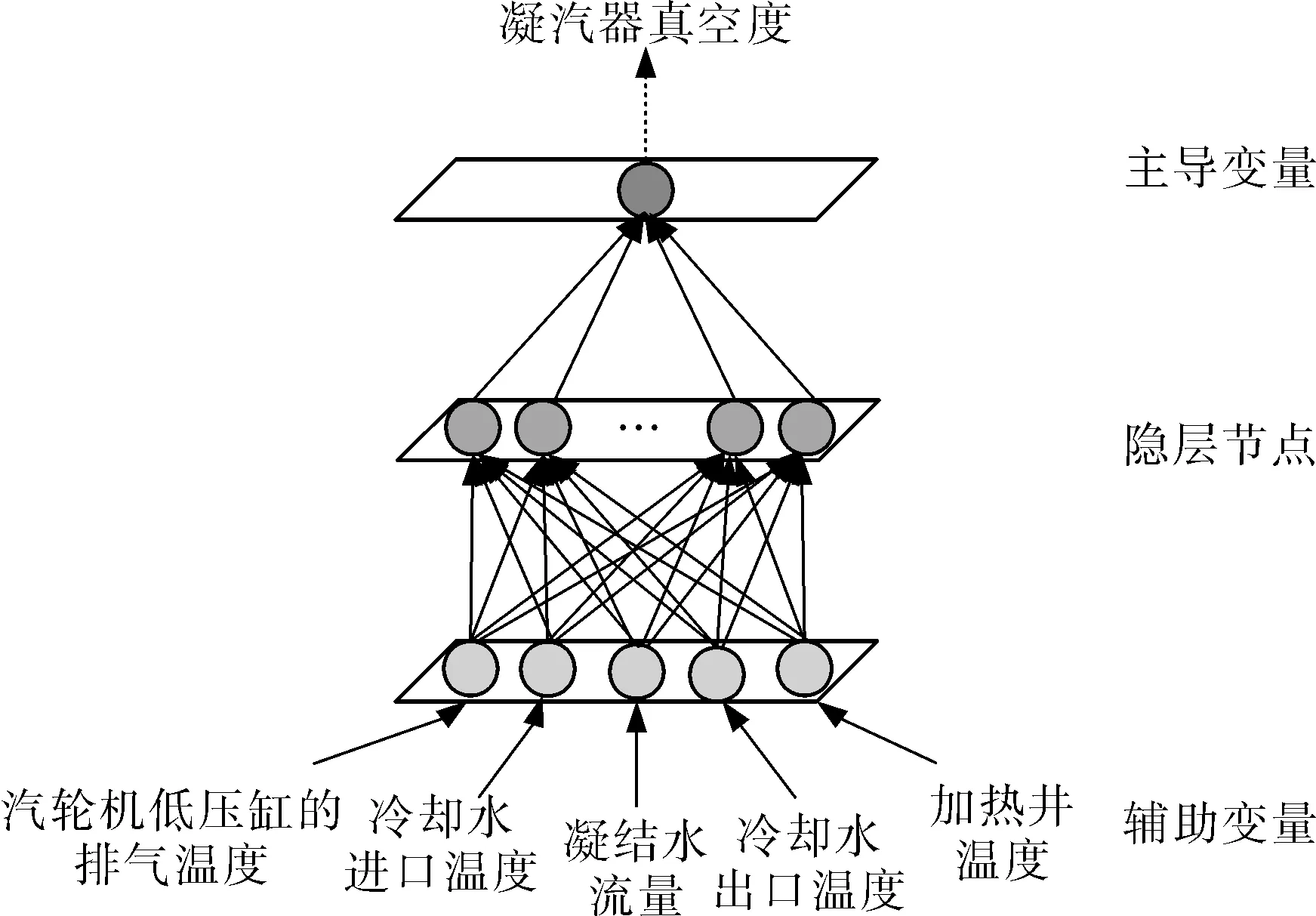
Neural Networks

2.2 模糊软集下的权重提取

依靠模糊软集实现组合预测模型的网络权重提取，涉及模糊软集的构建、隶属度确定及组合预测的基本概率赋值等，具体步骤如下[7]：

a. 定义论域U=[u1,u2,u3,u4]上的模糊软集(F,A)。U代表时间序列中的数据，A={c1,c2,c3}，ci(i=1,2,3)代表基于BP、Elman、RBF的网络预测方法，F：A→P(U)。

b. 令pij(i=1,2,3；j=1,2,3,4)是定义在模糊软集(F,A)上的变量，其模糊隶属度的定义可用来反映预测精度，f(pij)=1-a|yij-yj|/|yj|，其中yij为预测网络ci在第j天的预测值，yj为第j天的真实值，笔者取aBP=100，aElman=aRBF=80。

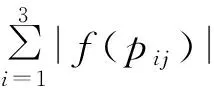
鉴于篇幅限制，更详细的解算过程和前四天单一网络预测模型的权重计算结果可参阅文献[2]。

2.3 Dempster组合规则下的权重融合模型

设网络预测值P1、P2和P3对应的权重分别为ω1、ω2和ω3，在识别框架Θ={P1，P2，P3}上建立基本可信度分配，其对应的基本概率赋值为：

mj(Pi)=ωi，i=1,2,3；j=1,2,3,4

(2)

按照式(1)，将对应于前两天的第一组数据和第二组数据对应的基本概率数进行第一重融合，即：

m(P1)=m1(P1)m2(P1)/(1-k)

m(P2)=m1(P2)m2(P2)/(1-k)

m(P3)=m1(P3)m2(P3)/(1-k)

(3)

k=m1(P1)m2(P2)+m1(P1)m2(P3)+m1(P2)×

m2(P1)+m1(P2)m2(P3)+m1(P3)m2(P1)+

m1(P3)m2(P2)

将融合后的基本概率数与第三组真空度预测值所对应的基本概率数进行第二重融合，再进行第三重融合，结果记为m1⊕m2⊕m3⊕m4，而计算所得的基本概率赋值记为mcombi(P1)、mcombi(P2)、mcombi(P3)，该组数据即在识别框架Θ={P1,P2,P3}上所建立的，随后一天组合模型进行真空度预测的融合权重，表示为：

(4)

第五天组合模型真空度预测数据融合的最终结果为：

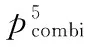
(5)

式(5)中，p15、p25、p35分别为3个单一网络对第五天真空度的预测结果。各重融合的权重计算结果见表1。

表1 各重融合的权重

2.4 基于组合证据冲突的修正算法

由表1可知，各重融合下k值分别为0.662 9、0.657 9、0.642 8，与1的接近程度表征证据可能出现一定程度的冲突，继续修正融合模型的权值，完成合成算法的基本概率再分配，具体步骤如下：

a. 当获得了连续4天的网络预测权值后，可知证据源中n=4，即证据集为Ei(i=1,2,3,4)。计算第i个证据Ei与其他证据Ej(i≠j)之间的冲突程度Kij(i=1,2,3,4;j=1,2,3,4)，即可构成证据Ei的冲突向量，表示为K1={K12,K13,K14}，K2={K21,K23,K24}，K3={K31,K32,K34}，K4={K41,K42,K43}。

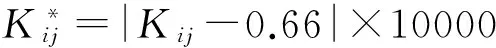
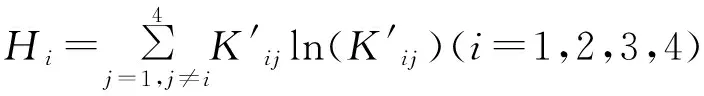
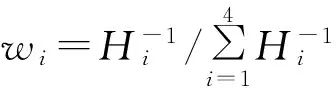
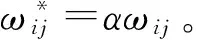
(6)

经上述解算，修正后的权重系数见表2。

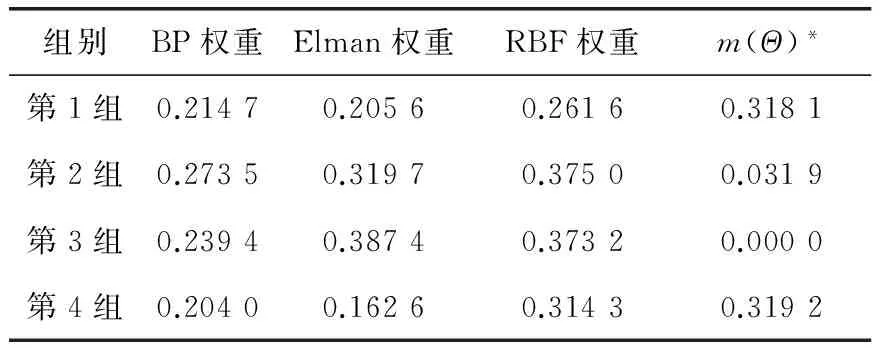
表2 权重系数修正结果

将修正后的权重系数代入新的合成公式，计算此时多重融合下证据的基本概率数和k值：

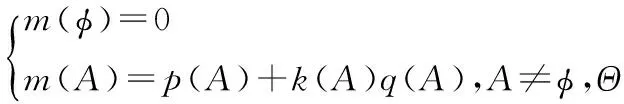
(7)

(8)

其中，p(A)为原合成公式形式，q(A)为证据对事件A的平均支持程度，k(A)为此时证据冲突概率。将k按比例分配给事件A，即实现证据冲突的概率按各个命题的平均支持度加权进行分配，结果如下：

f(A)=k(A)q(A)

(9)

笔者采用1和2组、3和4组分别融合，各计算结果再融合方式，各重融合结果见表3。

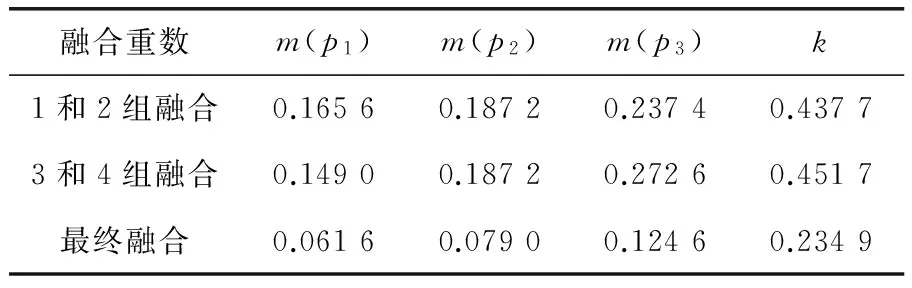
表3 权重系数修正的权重融合结果

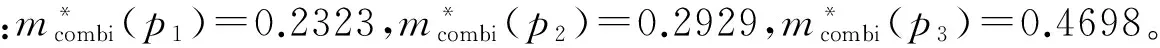
3 仿真和结果分析

第五天真空度实际值与预测值数据见表4。

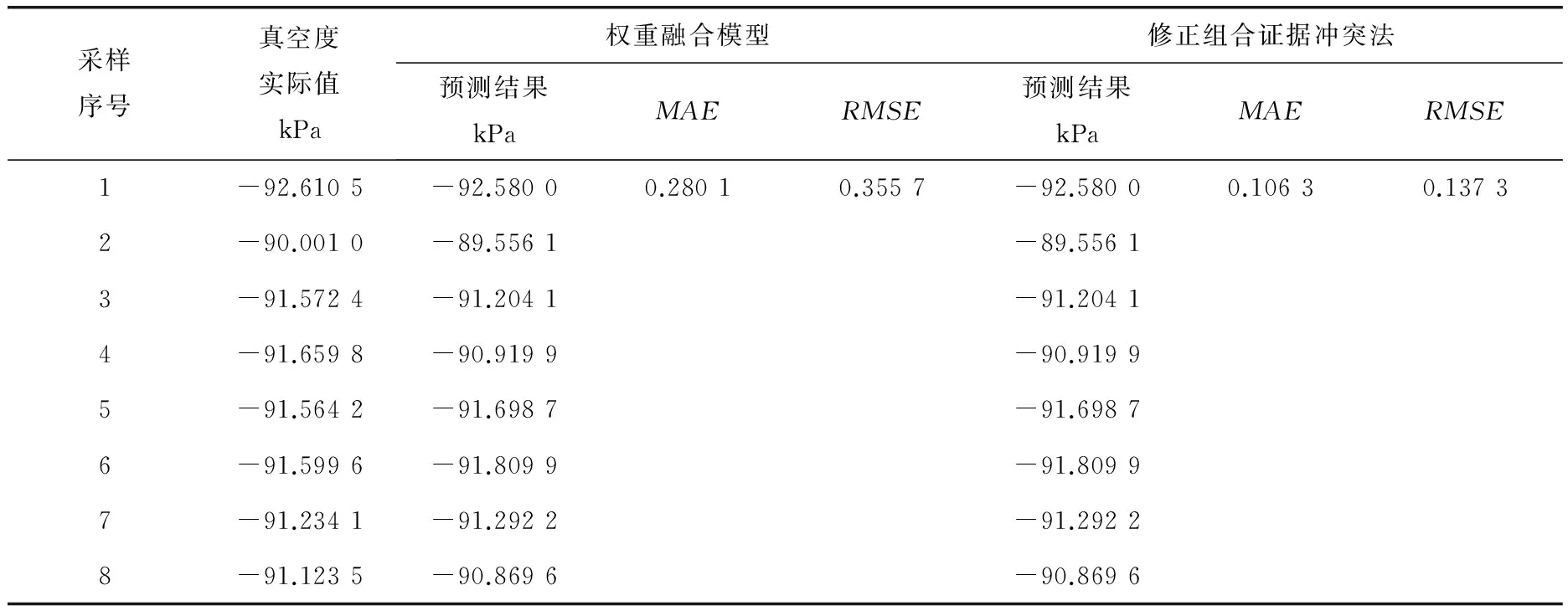
表4 第五天真空度实际值与预测结果分析

由表4数据可知，笔者所提算法在考虑D-S组合预测k值比较接近1的情况下，引入熵值和“折扣率”因子，修正了融合解算的权重提取算法。对比笔者所提方法和常规模糊软集下D-S预测结果，MAE和RMSE精度有较大程度的提升。图2为第五天的实际值与各预测值之间的直观对比图，相比之下，组合证据冲突修正算法的预测结果更接近实际值。

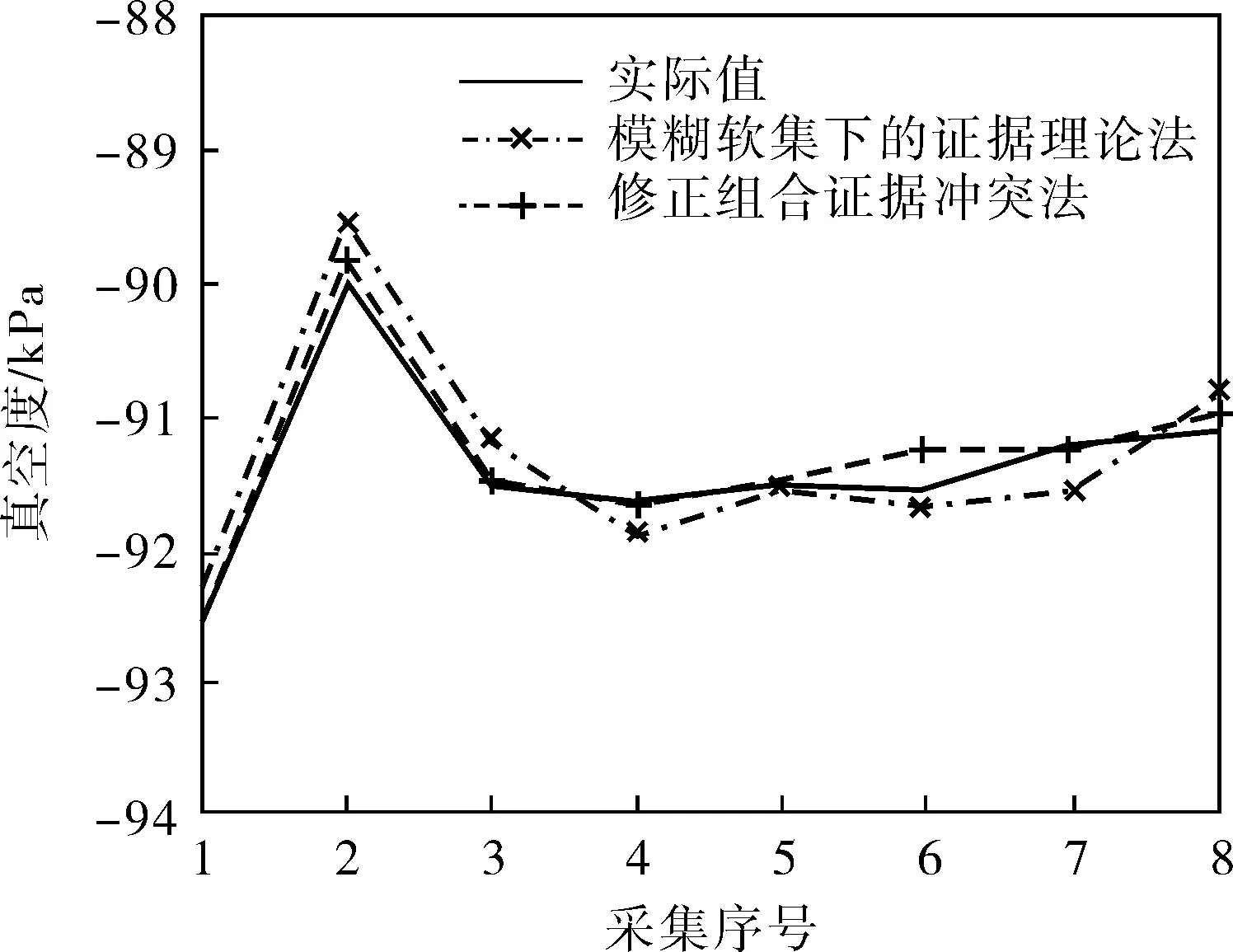
图2 不同方法下各预测值与实际值的对比

4 结束语

针对凝汽器真空度难以在线测量的问题，笔者基于离线训练、在线预测问题的智能求解策略，开展了Dempster组合证据框架下的真空度多网络融合预测，并对证据间冲突程度进行评价。为继续削减该值对预测结果的影响，引入熵和“折扣率”因子，实现了证据间冲突修正算法。在样本空间有限的情况下，对比不同方法下预测结果的MAE和RMSE值，应用修正算法所获得的统计值精度更高，表明其在一定程度上扩展了Dempster组合模型的应用场合和适用范围。

[1] 张炳文，陈跃.双压凝汽器低真空供热方案分析[J].化工机械，2012,39(4):540～544.

[2] 李勇，李立言，曹丽华，等.山谷型双流程凝汽器管侧流场的数值分析[J].化工机械，2012,39(3):351～355.

[3] Xiao Z,Gong K,Zou Y.A Combined Forecasting Approach Based on Fuzzy Soft Sets[J].Journal of Computational and Applied Mathematics,2009,228(1):326～333.

[4] 夏琳琳,台金娟,刘惠敏，等.权重提取与Dempster多重融合的凝汽器真空预测[J].沈阳工业大学学报,2015,37(3):329～334.

[5] 王秀芳,杨琦,田金燕.基于距离加权证据理论的管网泄漏诊断[J].化工自动化及仪表,2012,39(8):1001～1003.

[6] 高丙坤,严娓,岳茂兴.基于神经网络证据理论的天然气管道泄漏检测[J].化工自动化及仪表,2012,39(10):1268～1271.

[7] 牛东晓,范磊磊.基于模糊软集和DS证据理论的中长期负荷预测[J]．陕西电力,2013，41(6):6～8.