改进的细菌觅食算法求解多目标FJSP问题

金 花 宁 涛 刘 芳

(大连交通大学软件学院,辽宁 大连 116045)

多目标FJSP包括机器分配和工序排序两个子问题。吴俊和方锦明提出基于禁忌算法利用分步策略求解FJSP的两个子问题[2]。Chaudhry I A在考虑机器负荷平衡性的前提下，提出了一种选择累加工时较短机器的机器选择法，虽然这种方法提高了初始种群的质量，但增加了机器选择的复杂性[3]。刘晓冰等提出了包括机器选择链和工序顺序链的双链量子编码方法，但该方法对机器选择对工序顺序的影响考虑较少[4]。Deng G L和Gu X S提出了一种混合的离散差分进化算法求解非空闲置换流水车间调度问题，该算法用一种基于网络表示的加速方法对工件加工序列的邻域进行评价[5]。Mokhtari H等为了优化最大完工时间和总成本双目标，采用混合了可变邻域搜索和坐标方位搜索的DE算法，但他们对影响算法效率的因素分析不充分[6]。

笔者在分析FJSP的特点并总结已有文献方法优势和不足的基础上，提出利用模拟细菌觅食行为的改进细菌觅食算法(Improved Bacteria Foraging Optimization Algorithm,IBFOA)来求解FJSP[7]。

1.1 问题描述

FJSP的描述如下：车间有N个待加工工件并配有M台机器，每个工件i(i∈{1,2,…,N})包含ni(ni≥1)道工序，工序要按照指定的加工路线进行；Rij表示工件i的第j(j∈{1,2,…,ni})道工序，Mij(Mij⊆{1,2,…,M})表示可以加工工件i的第j道工序的机器集合，每道工序Rij可以在M台机器中有处理能力的任意一台机器m(m∈{1,2,…,Mij})上加工，机器m可以加工不同工件的多道工序[8,9]。问题包括机器选择和工序排序两个子问题。

1.2 目标函数

生产企业实现效益的首要目标是及时、高效地完成生产任务，因此FJSP首要的调度目标是最小化最大完工时间和最小化总成本。笔者设计了最小化工件的最大完工时间和最小化总成本目标模型，并建立目标函数，其中最小化最大完工时间模型如下：

f1=min(F)=min[max(Sijmtijm)]

(1)

其中，F为机器的完工时间，是衡量机器工作负荷的重要指标；tijm表示工序Rij在机器m上的加工时间；Sijm表示工件i的第j道工序在机器m上的加工状况(1表示加工，0表示未加工)。

最小化总成本模型如下：

(2)

Pijm=μijm+νijm

(3)

其中，P表示工件i的加工总成本；pi表示工件i的原材料成本；Pijm表示工序Rij在机器m上的加工成本；μijm表示工序Rij在机器m上的加工人工成本；νijm表示工序Rij在机器m上的加工机器成本。

1.3 约束条件

生产要求同一工件的工序间应有先后约束，即工件i的第j道工序必须在第(j-1)道工序完成后才可以开始，即：

(4)

其中，Sijm=Si(j-1)m=1；bijm表示工序Rij在机器m上的开始加工时间；bi(j-1)m表示工件i的第(j-1)道工序Ri(j-1)在机器m上的开始加工时间。

同一台机器在同一时刻只能加工一道工序，即对工序Rij在时刻t(t>0)时,若∃Sijm=1，则Sxym=1必不成立(当i=x时j≠y)。

2 改进的细菌觅食算法

基本的细菌觅食优化算法(Bacteria Foraging Optimization Algorithm,BFOA)[10]是一种基于全局随机搜索的算法，其主要操作包括趋化、复制和驱散；而趋化操作是BFOA的核心，其包括翻转和游动。但一般BFOA中应用的是定步长策略对问题进行求解，这限制了算法的收敛[11]。因此笔者提出了基于拥挤距离的自适应变步长调整策略IBFOA。改进算法的步骤描述如下：

a. 初始化操作。对细菌个体的位置Po、种群规模SP、趋化次数Nc、繁殖次数Nr和驱散次数Nd进行确定。

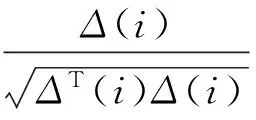
c. 复制操作。复制操作中引入繁殖阈和死亡阈两个概念。繁殖阈指如果细菌个体在游动过程中因为一直吸收营养而发展到可繁殖的程度则达到繁殖阈；死亡阈指若细菌个体在游动过程中因为没有吸收到足够的营养难以继续存活而被淘汰则达到死亡阈。计算细菌个体吸收的营养物质，分裂复制达到繁殖阈的优秀个体，淘汰低于死亡阈的劣质个体，如果细菌复制达到规定次数则转到驱散操作，否则转到趋化操作。

d. 驱散操作。如果菌落达到规定的驱散次数，则算法结束；否则，菌落将被驱散到任意方向，并转到步骤b重新进行趋化和复制操作。

3 数据分析与验证

3.1 算法性能实验与分析

为了验证所提出算法的有效性，笔者对包含10个算例的Brandimarte测试集进行测试[12]。针对10个算例分别运行IBFOA和其他算法的结果对比见表1，Tx表示最大完工时间，Cx表示加工成本；HVNSA表示基于变邻域的遗传禁忌搜索算法[13]；MADSA表示Seyed H A R等提出的两类多目标资源受限项目调度和多Agent分布式车间动态调度方法[14]。

表1 Brandimarte算例结果对比

由对比结果可知，使用IBFOA，对Tx有5次获得最优解；除了Mk04算例外，其余9个算例用笔者提出的算法求得的解都优于或等同于其他两个算法求得的解；除Mk04外，IBFOA计算的Cx值均不大于其他算法的值。因此，用IBFOA求解问题优于其他两种算法。

3.2 实例验证

以某化工设备加工车间的实际生产为例，进一步验证IBFOA解决多目标FJSP的性能。设备包括6个作业单位、8个装配工件和20道工序，作业单位包含1台机器设备，交货期单位为分钟。订单包括助力轴30件，要求30件的热处理同批进行，交货期为35 000min。设置迭代次数为200次，分别使用CPA[15]、MADSA和IBFOA对问题进行求解的调度结果见表2。可以看出，每个算法在设定的迭代周期内都可以得到少于交货期的解，其中IBFOA的最大完工时间为22 387min，相对于CPA，生产成本节约了5%。不同算法调度结果的比较如图1所示。

表2 不同算法的调度结果

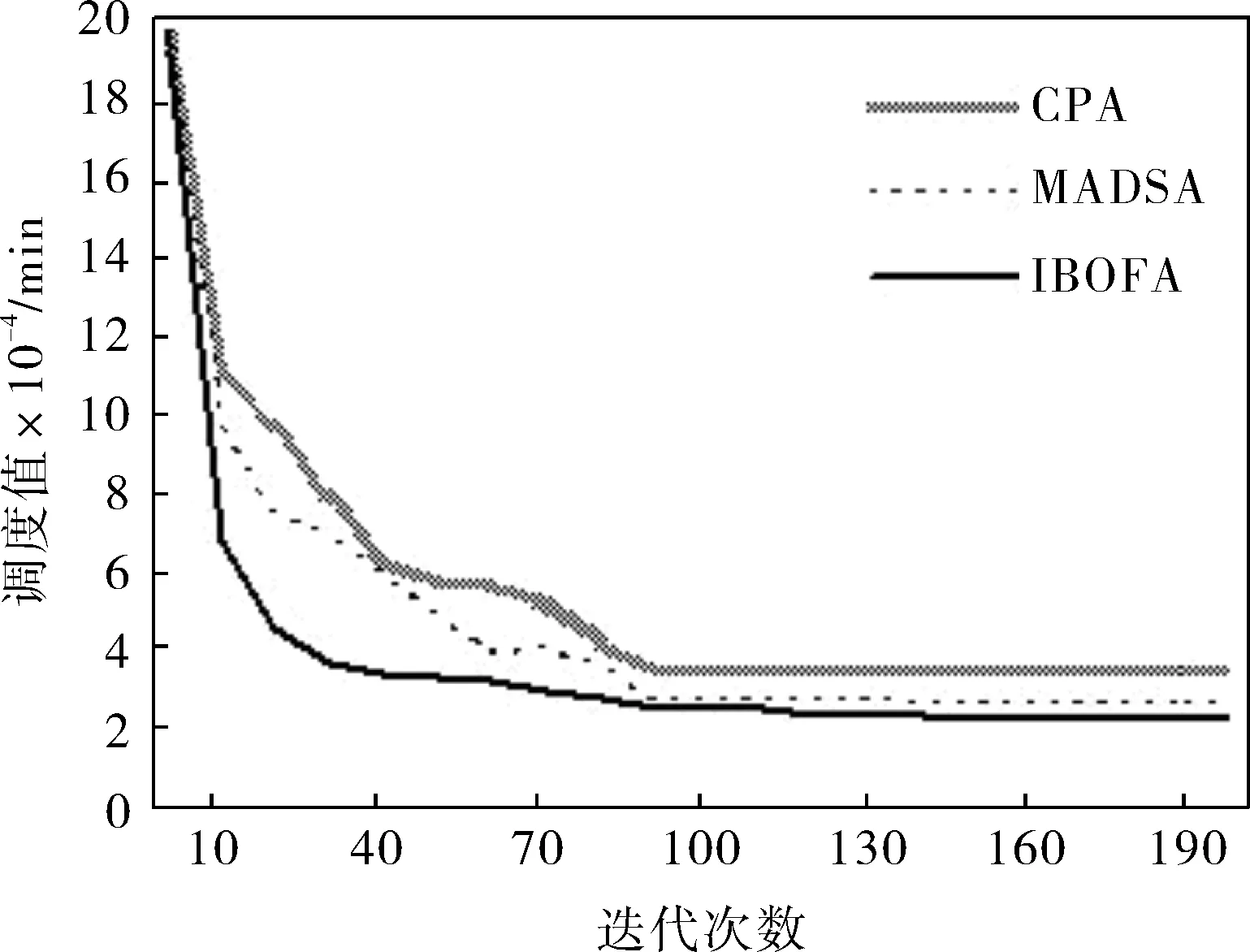
图1 不同算法调度结果比较

4 结束语

笔者根据约束条件不同，建立了多目标FJSP的数学模型，在基于调整趋化步长的基础上，提出了包括趋化、复制和驱散操作的改进细菌觅食算法。并以Brandimarte算例和某设备加工车间工件工序调度为例，对IBFOA、CPA和MADSA进行比较，结果表明：IBFOA获得了最小化最大完工时间和最小化总成本的目标，这也验证了IBFOA解决FJSP的有效性。

[1] Bagheri A,Zandieh M,Mahdavi I,et al.An Artificial Immune Algorithm for the Flexible Job-shop Scheduling Problem[J].Future Generation Computer Systems,2010,26(4):533～541.

[2] 吴俊,方锦明.采用排挤机制小生境技术改进禁忌搜索算法[J].化工自动化及仪表,2010,37(8):34～36.

[3] Chaudhry I A.Job Shop Scheduling Problem with Alternative Machines Using Genetic Algorithms[J].Journal of Central South University,2012,(19):1322～1333.

[4] 刘晓冰,焦璇,宁涛,等.基于双链量子遗传算法的柔性作业车间调度[J].计算机集成制造系统,2014,20(9):1～11.

[5] Deng G L,Gu X S.A Hybrid Discrete Differential Evolution Algorithm for the No-idle Permutation Flow Shop Scheduling Problem with Makespan Criterion[J].Computers & Operations Research,2012,39(9):2152～2160.

[6] Mokhtari H,Abadi I N K,Cheraghalikhani A.A Multi-objective Flow Shop Scheduling with Resource-dependent Processing Times:Trade-off between Makespan and Cost of Resources[J].International Journal of Production Research,2011,49(19):5851～5875.

[7] Shiv P,Deo P V.A Hybrid GABFO Scheduling for Optimal Makespan in Computational Grid[J].International Journal of Applied Evolutionary Computation,2014,5(3):57～83.

[8] 张静,王万良,徐新黎,等.混合粒子群算法求解多目标柔性作业车间调度问题[J].控制理论与应用,2012,29(6):715～722.

[9] 施进发,焦合军,陈涛.交货期惩罚下柔性车间调度多目标Pareto优化研究[J].机械工程学报,2012,48(12):184～192.

[10] 刘芹.差分进化细菌觅食算法求解公交车调度问题[J].交通运输系统工程与信息,2012,12(2):156～161.

[11] 崔静静,孙延明,车兰秀.改进细菌觅食算法求解车间作业调度问题[J].计算机应用研究,2011,28(9):3324～3326.

[12] Brandimarte P.Decision Making under Risk[M].New York:John Wiley & Sons Inc,2011.

[13] 张利平.作业车间预反应式动态调度理论与方法研究[D].武汉:华中科技大学,2013.

[14] Seyed H A R,Zandieh M,Yazdani M.Developing Two Multi-objective Evolutionary Algorithms for the Multi-objective Flexible Job Shop Scheduling Problem[J].The International Journal of Advanced Manufacturing Technology,2013,64(5-8):915～932.

[15] 刘爱军,杨育,邢青松,等.多目标模糊柔性车间调度中的多种群遗传算法[J].计算机集成制造系统,2011,17(9):1954～1961.