基于复杂网络的电网元件脆弱性分析
关学忠 刘金龙 高 哲 于 镝
(1.东北石油大学电气信息工程学院,黑龙江 大庆 163318;2.海洋石油工程股份有限公司,天津 300461;
3.辽宁大学轻型产业学院,沈阳 110036)
随着社会的发展和人们生活水平的不断提高,电力成为人类不可或缺的资源。人们越依赖电力,电网的覆盖面积也就越大。电网已经成为当今世界覆盖面积最广、结构最复杂的人造网络之一。为了确保人们的正常生活就需要一个稳定的电网运行环境,但是仍然有很多大规模停电事故时常发生[1~5]。因此,要确保电力网络安全稳定地工作就要保护电网的元件设备,但是电网的元件和设备数目十分巨大,不可能进行逐一保护,于是,电力专家把保护的重点放在了关键节点和线路上。
从20世纪50年代开始,专家学者们对网络系统的研究愈发重视起来。根据近年来的研究发现,许多实际网络的节点连接度没有明显的特征长度(这种网络被称为无标度网络),其中典型的一种是Barabási A L和Albert R于1999年提出的BA无标度网络,该模型是基于实际网络中具有的增长特性和优先连接特性构成的,因此,无标度网络更贴近电力网络[6,7]。Holme P等定义了线路的度,把线路两端节点的度分别经过乘积、求和、求最大值和最小值处理,结果发现线路两端节点度经过乘积运算的形式最符合线路的度[8]。Comin C H和Costa L D F研究了度与介数之间的关系,即通过一个最优参数把两者联系起来形成一个新的指标来评价节点在网络中的重要性[9]。Hou B N等提出了一种复合指标,该指标是把度、介数和k-核3个不同的指标通过欧拉距离公式结合起来形成的,该方法综合考虑了度、介数和k-核对节点在网络中重要性的影响,该指标比单纯的指标更能有效地评价节点的重要性[10]。
在此,笔者把电力网络抽象和简化成为一个由节点和线路组成的复杂网络,通过复杂网络理论来研究节点及线路等电网元件对整个网络的重要性,用节点及线路等元件的特性参数来评价电力网络各方面的脆弱性。最后以IEEE-118总线系统为模型,通过联锁故障模拟来研究节点和线路在整个电力网络输电性能上的脆弱性。
1 电力网络的抽象和简化
以复杂网络为基础来研究电力网络,需要对电力网络进行抽象和简化。把发电厂、变电站和中间连接点看作网络的节点,输电线和变压器支路是网络的线路,线路的权值是其阻抗值,两个相连节点之间有且仅有一条线路存在,无自环和重边。忽略发电厂主接线,将发电机看作在其节点上注入有功功率。忽略变电站主接线,将变电站看作在其节点上注入有功功率。不考虑全部的对地支路。不合并同杆并架和平行多回的输电线路,其权值取各自权值。电能是沿着发电机节点到负荷节点之间所有线路传输的。需考虑的因素有:电网中每个节点的电气介数上限和度上限,每个发电机节点的额定发电容量,每个负荷节点的最大负荷需求,每条线路的电气介数上限和度上限。
经过上述抽象和简化,可以得到一个有向加权网络G=(N,M),其中N是节点的集合,节点的数量为n;M是线路的集合,线路的数量为m。电能方向总是从发电机节点到负荷节点的,发电机节点i与负荷节点j之间某个路径沿线的线路效能的有效组合称为路径的效能εij,即有:
εij=[∑1/egh]-1
(1)
其中,(g,h)∈O,O是该路径沿线线路标号的集合;egh是路径gh的线路效能。在一对发电机节点和负荷节点之间所有的路径中效能最大的称为最有效路径,最有效路径可以表现出这对节点之间的电能输送能力。则整个网络的所有发电机节点和负荷节点之间的最有效路径的平均值就是全局效能E,全局效能反映了整个电网的电力传输能力,其表达式为:
(2)
式中nG、nL——发电机节点和负载节点的数量;
NG、NL——发电机节点和负载节点的集合。
2 电网元件的特性参数
2.1 线路的电气度介数指标和节点的电气三重数指标
通过Comin C H和Costa L D F提出的方法把线路的度和线路的电气介数有效结合起来可以得到线路(x,y)的电气度介数Λ(x,y),其表达式为:
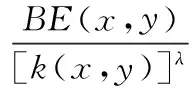
(3)
其中,BE(x,y)是线路(x,y)的电气介数;k(x,y)是线路(x,y)的度;kx和ky分别为该线路两个端点的度;UG和UL分别代表发电机节点集合和负荷节点集合;Qxy(i,j)是发电机节点i和负荷节点j分别注入Qi=1和Qj=-1时,线路(x,y)上产生的有功功率;wij=(Si,Sj)表示发电机节点i和负荷节点j之间最大的能用的传输功率,即从i向j传输的电能权重,其中Si是节点i的额定发电容量,Sj是节点j的最大负荷需求;λ是线路电气介数与度之间的最优参数。
电网中有发电机节点、负荷节点和传输节点3类,因此根据节点的不同类型,节点的电气三重数指标的计算方式也分为3种。通过Hou B N等提出的方法,把节点的度、节点的k-核值和节点的电气介数有效结合起来得到的节点u的电气三重数指标Δ(u)的表达式为:
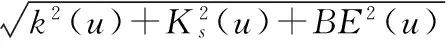
(4)
式中BE(u)——节点u的电气介数;
k(u)——节点u的度;
Ks(u)——节点u的k-核值。
为便于分析节点u的电气三重数指标特性,将式(4)写成如下形式:
(5)
其中,BE(u,v)是以节点u和节点v为端点的线路的电气介数;V(u)是与节点u邻近节点的集合,v是该集合里的一个节点;当节点u是发电机节点时,wui=(Su,Si)表示发电机节点u和负荷节点i之间最大的能用的传输功率,即从u向i传输电能的权重,其中Su是节点u的额定发电容量,Si是节点i的最大负荷需求;当节点u是负荷节点时,wiu=(Si,Su)表示发电机节点i和负荷节点u之间最大的能用的传输功率,即从i向u传输电能的权重,其中Si是节点i的额定发电容量,Su是节点u的最大负荷需求;当节点u是传输节点时,即u∉UG且u∉UL时,则不考虑这种情况。
2.2 线路和节点的承受性系数
线路(x,y)的电气度介数超过其上限导致该线路的传输电能效率下降的过程,可以用线路效能exy的降低来反映,那么时刻t的线路效能的迭代规则为:
(6)
其中,exy(0)是线路(x,y)初始时刻的效能;exy(t+1)是线路(x,y)在t+1时刻的效能;Λxy(t)是线路(x,y)在t时刻的电气度介数;Γxy是线路(x,y)的电气度介数上限,其具体表达式为:
Γxy=γM·Λxy(0)
(7)
式中γM——线路的承受性系数;
Λxy(0)——线路(x,y)初始时刻的电气度介数。
在电力网络中,线路是具有最大耐受能力的,因此BEmax(x,y)=αM·BExy(0)为线路(x,y)的电气介数上限,BExy(0)为初始时刻线路(x,y)的电气介数,αM>1是线路的耐受性系数。线路连接的两个节点与其他节点相连的数目也是有限的,因此,线路(x,y)的度上限kmax(x,y)=βM·kxy(0),其中kxy(0)为初始时刻线路(x,y)的度,βM>1是线路的连接性系数。这里定义线路的耐受性系数αM和线路的连接性系数βM之间的最小值为线路的承受性系数γM,即γM=min(αM,βM)。
节点u的电气三重数指标超过其上限导致该节点与其邻近节点相连的线路(u,v)传输电能效率下降的过程,可以用线路效能euv的降低来反映,那么时刻t的线路效能的迭代规则为:
(8)
其中,euv(0)是线路(u,v)初始时刻的效能;euv(t+1)是线路(u,v)在t+1时刻的效能;Δu(t)是节点u在t时刻的电气三重数指标;Ψu是节点u的电气三重数指标上限,其具体表达式为:
Ψu=γN·Δu(0)
(9)
式中γN——节点的承受性系数;
Δu(0)——节点u初始时刻的电气三重数指标。
在电力网络中,节点是具有最大耐受能力的,因此BEmax(u)=αN·BEu(0)为该节点的电气介数上限,BEu(0)为初始时刻节点u的电气介数,αN>1是节点的耐受性系数。而与节点相连的线路数目也是有限的,因此,节点u的度上限kmax(u)=βN·ku(0),ku(0)为初始时刻节点u的度,βN>1是节点的连接性系数。这里定义节点的耐受性系数αN和节点的连接性系数βN之间的最小值为节点的承受性系数γN,即γN=min(αN,βN)。
3 仿真分析
3.1 元件移除策略
仿真中对于元件的移除包括线路和节点的移除。元件的移除策略有5种:随机线路移除,随机选取一条线路进行移除;电气介数线路移除,选取初始状态电气介数最高的线路进行移除;随机节点移除,随机选取一个节点进行移除;电气介数节点移除,选取初始状态电气介数最高的节点移除;综合元件移除,首先选取初始状态电气三重数指标最高的一个节点进行移除,如果在移除该节点时把初始状态电气度介数最高的线路也已经一并移除则不再移除其他线路,否则再取初始状态电气度介数最高的一条线路移除。
3.2 仿真模型
最常用、最经典的电力网络模型是IEEE-118总线系统(图1),它具有一般实际电力网络具有的小世界特性和无标度特性。该系统有54个发电机节点、54个负载节点和10个传输节点,按总线分有54个发电机总线、64个负载总线和186个传输总线。
3.3 仿真移除策略
根据上述得到的节点的电气三重数指标、线路的电气度介数指标和两者在联锁故障模拟中对于全局效能影响的迭代公式,可以得出仿真的具体步骤为:
a. 构建电网拓扑结构模型;
b. 计算初始状态每个节点的电气三重数指标和电气三重数指标上限,计算初始状态每条线路的电气度介数指标和电气度介数指标上限;
c. 计算初始状态每条线路的效能和电网全局效能;
d. 确定元件移除策略并按预定的策略移除特定元件;
e. 计算当前状态每个节点的电气三重数指标;
f. 计算当前状态每条线路的电气度介数指标;
g. 计算当前状态的电网全局效能;
h. 判断是否有其他过载的节点,如果有则移除相应的过载节点和相连线路,然后按式(8)重新计算每条线路的效能并转至步骤h,如果没有则转至步骤i;
i. 判断是否有其他过载线路,如果有则移除相应的过载线路,然后按式(6)重新计算每条线路的效能并转至步骤e,如果没有则转至步骤j;

图1 电力网络模型IEEE-118总线系统
j. 计算最终状态的电网全局效能。
3.4 仿真结果
对元件采用5种移除策略,通过动态分析法得到综合承受性系数对电网全局效能的影响曲线(图2)。从仿真结果来看,5种移除策略对网络性能的破坏是不同的。网络对随机节点攻击和随机线路攻击有很强的鲁棒性,但是对节点电气介数攻击、线路的电气介数攻击和综合指标攻击这3种蓄意攻击有很高的脆弱性,尤其是对综合指标攻击的脆弱性是最高的。
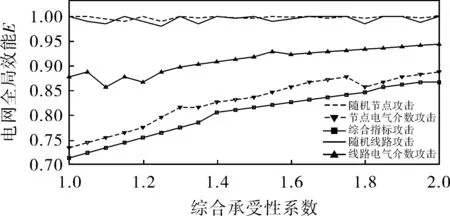
图2 综合承受性系数对电网全局效能的影响曲线
4 结论
4.1攻击高电气三重数指标的节点和攻击高电气度介数指标的线路比其他攻击策略要更能够降低电网的性能。
4.2移除具有高电气三重数指标的节点和高电气度介数指标的线路可以更有效地降低整个电网的输电性能。
4.3对IEEE-118模型的仿真结果表明:高电气度介数指标的线路和高电气三重数指标的节点对整个电力网络的结构和特性都有很大的影响,这些节点和线路是电力网络中的最重要和最关键的元件,只有加强对它们的保护,才能保障电网的安全稳定工作。
[1] Petreska I,Tomovski I,Gutierrez E,et al.Application of Modal Analysis in Assessing Attack Vulnerability of Complex Networks[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(4):1008~1018.
[2] 鲁顺,高立群,王坷,等.莫斯科大停电分析及启示[J].继电器,2006,34(16):27~31.
[3] 林伟芳,孙华东,汤涌,等.巴西“11·10”大停电事故分析及启示[J].电力系统自动化,2010,34(7):1~5.
[4] 林伟芳,汤涌,孙华东,等.巴西“2·4”大停电事故及对电网安全稳定运行的启示[J].电力系统自动化,2011,35(9):1~5.
[5] 方勇杰.美国“9·8”大停电对连锁故障防控技术的启示[J].电力系统自动化,2012,36(15):1~7.
[6] Barabási A L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999,286:509~512.
[7] Barabási A L.Scale-Free Networks:A Decade and Beyond[J].Science,2009,325:412~413.
[8] Holme P,Kim B J,Yoon C N,et al.Attack Vulnerability of Complex Networks[J].Physical Review E,2002,65(5):1~15.
[9] Comin C H,Costa L D F.Identifying the Starting Point of a Spreading Process in Complex Networks[J].Physiccal Review E,2011,84(5):84~86.
[10] Hou B N,Yao Y P,Liao D S.Identifying all-around Nodes for Spreading Dynamics in Complex Networks[J].Physica A:Statistical Mechanics and Its Applications,2012,391(15):4012~4017.

