基于模糊多准则决策扩展方法的分模线选择和评估研究

李坤鹏 董长虹

(北京航空航天大学，北京 100083)

在模型设计领域，分模线的生成和选择是最重要的研究方向之一[1]，然而，当模制部件比较复杂时，许多现有方法可能无效[2]。近期有学者提出几种最优分模线选择方法和准则[3]，然而，大多数方法都基于准确测量和清晰评估理论,因此，要想使用语言变量来表示分模线适合度的准则权重和评估结果，还需做进一步研究[4]。

多准则决策(Multi Criteria Decision Making,MCDM)方法广泛用于选择和评估备选方案领域。由于大部分模糊MCDM问题中备选方案的最终评估值是模糊数，因此需要采用适当的排序方法将这些模糊数解模糊成清晰的决策排序值。目前已有学者提出多种求解模糊MCDM问题的方法[5,6]，但这些方法大多不能从最终评估值的隶属函数中给出解模糊公式，限制了现有模糊MCDM方法的应用范围[7,8]。其中也有模糊数排序方法能够将模糊数解模糊成清晰值，但都不能保证每种情况下结果一致，甚至有些无法给出判定结果[9]。为此，笔者提出一种扩展模糊MCDM方法来解决分模线的选择和评估问题。

分模方向、分模线和分模面是在模具整体结构和加工成本中起决定性作用的因素。分模方向是模片分离的方向，分模线是部件表面模片汇合的连续闭合曲线，分模面是模片组合时的接触面。图1所示为一个手机套模型的分模方向、分模线和分模面，进一步产生了两个模片。

图1 手机套模型

对于简单部件，很明显仅有一条分模线是最适合的曲线，然而，对于许多带有自由曲面的复杂部件，会生成多条分模线，设计者必须从中选择一条最适合的。因此，如何定义从候选方案中选择最优分模线的准则便成了一个重要的问题。

许多学者研究过分模线选择问题，文献[2]定义了一种包含9条决策的准则集，利用计算机辅助设计分模线和分模面。然而，这些准则有些是可量化的，有些是不可量化的，通过以下条件选择分模线/面：

∑wicij≤∑wicik,for allk

其中，cij是分模线/面j在准则Ci下的评估值，wi是准则Ci的权重系数。然而，文献[2]没有给出任何确定准则权重系数的建议。

文献[3]提出一种算法，使用组合因子-可视化程度(VF1和VF2)、分模面平整度(FF)和拉伸深度(DDF)来确定分模方向、分模线和分模面，整体因子(OF)用于评估衡量4个因子对候选的分模方向和对应分模线的累积影响。4个因子的权重系数wj(j=1～4)的理论值范围为[0，1]。然而，文献[3]在确定最佳分模方向和对应分模线时所有权重都设成了统一值，因此，这个方法不能准确反映每个准则的作用。

笔者使用模糊MCDM方法来实现最优分模线的选择。

2 模糊MCDM扩展模型的建立

2.1 备选方案在准则下的总评级

假设由一个有k(Dt,t=1,…，k)个决策者的委员会在h(Cj,j=1,…,h)个选择准则下评估m(Ai,i=1,…,m)个备选方案，则MCDM问题的矩阵形式可表示为：

C1C2…Ch

令xijt=(eijt，fijt，gijt)为决策者Dt在准则Cj下分配给备选方案Ai的评级适合度，平均评级适合度xij=(eij，fij，gij)可表示为：

(1)

2.2 总重要性权值

令wjt=(ojt,pjt,qjt)为决策者Dt对准则Cj分配的权重，包含k个决策者的委员会对准则Cj评估的平均权值wj=(oj,pj,qj)可表示为：

(2)

2.3 备选方案在准则下的规范化性能

准则分成效益型准则(B)和成本型准则(C)，效益型准则具有越大越好的特征。为了确保平均评级适合度和平均权值之间的兼容性，将平均评级适合度规范化为可比较尺度，假设rij=(aij,bij,cij)是备选方案i在准则j上的性能，则规范化后的xij可表示为：

(3)

2.4 规范化加权评级的隶属函数

(4)

利用两个方程来求解，即：

Aiα2+Biα+Qi-x=0

(5)

Ciα2+Diα+Zi-x=0

(6)

(7)

(8)

为了方便，将Ti表示为Ti=(Qi,Yi,Zi;Ai,Bi;Ci,Di)。

2.5 解模糊化

笔者采用文献[10]提出的一种新颖排序方法将每个备选方案的所有最终评估值解模糊化。

假设有m个模糊数Ai，i=1,2,…,m，每个模糊数有一个三角形隶属函数fAi(x)，按照文献[10]提出的排序算法对这m个模糊数两两比较，最大集M的隶属函数fM(x)为：

(9)

最小集G的隶属函数fG(x)为：

(10)

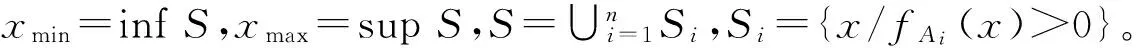
每个备选方案Ai的右效用值为：

(11)

(12)

(13)

(14)

每个乐观指标为α的模糊数Ai的总效用值为：

(15)

乐观指标α表示决策者的乐观程度，如果α>0.5，则表示决策者相当乐观。相反，则表示决策者相当悲观，如果α=0.5，则决策者中立，文中设定α=0.5。

2.6 获得排名值

运用每个Ai的总效用值解模糊化所有最终模糊评估值Ti，Ti的左右效用值表达式为：

(16)

(17)

(18)

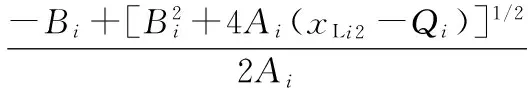
(19)

其中:

乡土树种具有适应当地气候条件，成活率高、生长快，充分代表了当地的文化特色和地域特色，且乡土树种是经过长时间沉淀积累下来的适宜本土生长的植物种类；乡土树种运输费用以及种植费用低，维护管理成本也低。为此在绿化树种选择上，要坚持以乡土树种为主，实践得知，美丽乡村绿化绿化乡土树种占绿化苗总量应把握在65%左右。除此之外，为增加生物多样性及观赏性，适当引进一些优良适生树种，丰富植物种类。

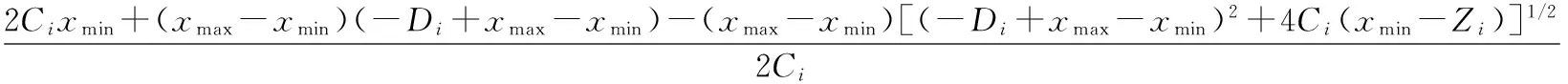
(20)

(21)

(22)

(23)

则Ti在乐观指标α=0.5时期的总效用值为：

(24)

3 验证分析

3.1 实验验证

假设设计者期望为一个模具选择一条最佳的分模线，A1、A2和A3是模具部件的3个可行分模线(图2、3)。D1、D2和D3是评估3条分模线的3个设计师，分模线评估基于4个准则：投影面积(C1)、底切(C2)、平整度(C3)和起模(C4)[1]。

图2 用来选择分模线的模具

图3 模制部件的分模线选择

计算过程为：

a. 备选方案准则下的总评级。设定用语言变量和相关的三角形模糊数表示在准则C1、C2、C3和C4下评估分模线A1、A2和A3的等级。

b. 总重要性权值。假设用语言加权集合和相关的模糊数来评估所有准则的重要性。使用式(2)计算每个决策者给出的4个准则的重要性权值和总权值。

c. 备选方案与准则的规范化性能。为简单实用，文中定义的所有模糊数在闭区间[0，1]内以省略规范化过程。

d. 求每个规范化加权评级的隶属函数。使用式(4)～(8)可获得最终的模糊评估值。

e. 解模糊化。使用式(16)～(19)和表1可获得每个备选方案的左右效用值，然后，使用式(10)～(13)两两比较备选方案进一步获得每个备选方案的左效用值、右效用值和总效用值(表2)。表2中的结果证实了笔者提出的方法对算例的适用性。由表2可知，在3条分模线中，第二条分模线A2的总效用值比A1和A3的大，第三条分模线A3的总效用值比A1的大，因此分模线的优劣排序为A2>A3>A1。所以，最好的分模线是A2。

表1 每个备选方案的最终模糊评估值

表2 A1、A2、A3两两比较的左右效用值和总效用值

3.2 比较分析

本节比较了笔者提出的方法与传统模糊MCDM方法。根据文献[12]中的例子，某公司期望为新建工厂选一个有效的位置，在这个问题中，A1、A2和A3是3个可行位置，由4个专家组成的委员会在5个效益型准则和一种成本型准则下做出评估，准则分别为：当地气候(C1)、需求区域(C2)、扩展可能性(C3)、可用交通(C4)、劳动力质量(C5)和投资成本(C6)。

使用式(4)～(8)和式(20)～(23)，两两比较备选方案可以得到每个备选方案的左效用值、右效用值和总效用值(表3)。从表3可以看出，3个位置的优劣排序为A2>A1>A3。因此，最佳位置是A2。该结果与文献[11]中提到的传统模糊MCDM方法一致，由此体现了笔者方法的适用性。

表3 针对文献[10]例子笔者方法对A1、A2、A3两两比较的结果

4 结束语

分模线选择和评估是一个MCDM问题，受多个准则的影响，笔者提出一种扩展的模糊MCDM方法来求解模具设计中的分模线选择和评估问题。在笔者提出的方法中，将分模线适应度的备选方案评级和相关准则重要性权值表示成语言值，由三角模糊数表示，然后求出每个准则下每条分模线的规范化加权评级隶属函数，为了避免进行复杂的模糊数计算，将这些规范化加权评级解模糊成清晰值，利用新型的最大最小集排序方法确定备选方案的优劣排序。通过实验证明了提出方法的适用性，在类似的设置下也可以应用到其他领域的问题，扩大了适用范围。

[1] Singh R, Madan J. Systematic Approach for Automated Determination of Parting Line for Die-cast Parts[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(5): 346～366.

[2] 李林鑫,周基友,陈显均.UG及PowerMILL在拨叉锻造模具设计制造中的应用[J].模具制造,2012, 31(4): 17～19.

[3] Chakraborty P, Venkata Reddy N. Automatic Determination of Parting Directions, Parting Lines and Surfaces for Two-piece Permanent Molds[J].Journal of Materials Processing Technology,2009, 209(5): 2464～2476.

[4] Yin Z P, Ding H, Li H X, et al. Geometric Mouldability Analysis by Geometric Reasoning and Fuzzy Decision Making[J].Computer-Aided Design, 2008, 36(1): 37～50.

[5] Xia M, Xu Z, Zhu B.Geometric Bonferroni Means with Their Application in Multi-criteria Decision Making[J]. Knowledge-Based Systems, 2013, 40(6): 88～100.

[6] Liao H, Xu Z. A VIKOR-based Method for Hesitant Fuzzy Multi-criteria Decision Making[J]. Fuzzy Optimization and Decision Making,2013,12(4): 373～392.

[7] 胡军华,张砚.基于相似度的区间二型模糊多准则群决策方法[J].系统工程与电子技术,2013,35(6):1242～1248.

[8] Chauhan A, Vaish R. Hard Coating Material Selection Using Multi-criteria Decision Making[J].Materials & Design,2013, 44(5):240～245.

[9] Mosadeghi R, Warnken J, Tomlinson R, et al. Uncertainty Analysis in the Application of Multi-criteria Decision-making Methods in Australian Strategic Environmental Decisions[J].Journal of Environmental Planning and Management, 2013, 56(8): 1097～1124.

[10] Chou S Y, Dat L Q, Vincent F Y.A Revised Method for Ranking Fuzzy Numbers Using Maximizing Set and Minimizing Set[J].Computers & Industrial Engineering,2011,61(4):1342～1348.

[11] Wang Y J.Fuzzy Multi-criteria Decision-making Based on Positive and Negative Extreme Solutions[J].Applied Mathematical Modelling,2011,35(5):1994～2004.