对于带有色噪声的多传感器系统两段辨识信息融合算法

李 恒，韩 波，2，王戴木，赵正平，刘争艳，李怀敏

(1. 阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037;2. 东南大学 毫米波国家重点实验室，南京 210096)

瑞典皇家科学院院士、著名控制理论专家Ljung L. (荣)对于系统辨识的定义为:按照一个准则，在模型类中选择一个与数据拟合最好的模型。［1］对于一个线性系统来说，建立模型的过程一般来说分为两步:模型结构辨识和模型参数辨识。［2］自回归滑动平均模型(Auto Regressive Moving Average Model)简称ARMA 模型，是自动控制领域里的一个重要模型，在工程、经济和生活等领域都得到了应用。［3］对于一个ARMA 模型来说，结构确定后，对参数的值进行辨识便是系统辨识的最终问题。参数辨识方法应用最为普遍的是递推最小二乘法，其优点在于不必知道被估计量和观测量的任何统计信息。［4］然而，当存在未知参数和噪声方差时，特别是系统中存在有色噪声时，递推最小二乘法便不能给出无偏估计，则此时需要用到最小二乘法的一些推广形式，如递推辅助变量法(RIV法)、递推增广最小二乘法、偏差补偿最小二乘法、遗忘因子法、广义最小二乘法、偏差补偿法和多级最小二乘法等。［5］以RIV 法为例，在结构上完全等同于递推最小二乘法，只是将其中的某些变量用相应的辅助变量代替。［6］通过这些推广方法可以对系统中存在的未知参数和噪声进行辨识。

多传感器信息融合广泛应用于系统辨识和信号处理理论中。［7］多传感器理论一般要求模型噪声和系统参数是已知的，然而在实际系统中，往往存在部分参数和噪声未知的情形。如在GPS 导航系统中，作为导航环境函数的矩阵往往包括大气时滞、多路位置误差、时钟漂移等，难以做出先验预测，因此需要在线自校正估值。［8］对于带未知噪声的系统，利用Kalman 滤波理论设计自校正估值器，需要在线辨识系统的噪声方差和协方差。［9］在理论设计中，绝大多数数据处理理论都假设噪声为白噪声，如文献［8，10］都提出了对于带含有白噪声的ARMA 系统进行辨识。但是文献［8，10］在设置环境时还是比较简单，比如每一种噪声都为白噪声。而在实际观测和数据处理中，各种噪声都是具有一定时间相关或者空间相关的有色噪声。［11］本文即拟设置一个带未知的有色的观测噪声以及未知白色公共干扰噪声的多传感器系统环境，按照一定的规则，构造一个多传感器信息融合多段辨识算法，并证明辨识方法具有强一致性。用一个仿真例子做了说明。

1 问题的提出

考虑一个多传感器系统

假设yi(t)为第i 个传感器的输出信号，s(t)为输入信号，w(t)和ηi(t)分别是第i 个传感器的输入噪声和观测噪声，ξ(t)为公共干扰噪声，ηi(t)为有色噪声且有形式:

假设多项式A(q－1)、C(q－1)和Pi(q－1)是稳定的，这些多项式具有形式X(q－1)= x0+ x1q－1+...+ xnxq－nx，q－1为滞后因子，q－1x(t)= x(t－1)，其中A(q－1)和C(q－1)的结构和参数都是已知的，也就是说完全已知的;Pi(q－1)的结构已知，而参数未知。vi(t)、w(t)和ξ(t)是零均值不相关的白噪声，噪声方差、和未知。观测yi(t)(i = 1，…，L)以概率1 有界。问题是对系统式(1)和(2)，在以上假设下，基于观测yi(t)(i = 1，…，L)如何估计Pi(q－1)的未知模型参数及噪声统计方差、和的值。

2 辨识算法

第1 段 辨识自回归参数。

由式(1)、(3)代入(2)中有

定 义 zi(t): = A(q－1)yi(t)，(q－1): =Pi(q－1)C(q－1)，(q－1):= A(q－1)Pi(q－1)，则式(5)可变为

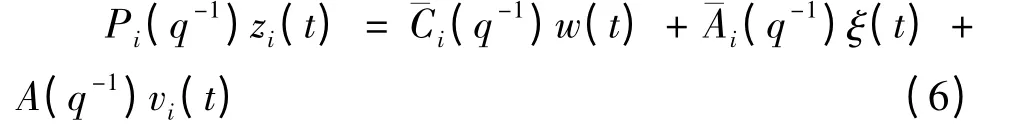
第2 段 辨识未知噪声方差。

定理对于一个带噪声的用式，和表示的多传感器模型，在假设下，所得的参数估计，以及噪声方差和有

证明:利用RIV 的收敛性［16］可证明1 式，利用初等函数的连续性和(k)的遍历性［13］可以证明其余式子。

3 例子

设有系统如式(1)－(3)所示，设na=2，nc= 1，npi= 1，a1= 0.6，a2=－0.2，p1= 1，=0.8，=0.2，=0.1，=0.2，=0.3，其中p1、、和σ2vi(i =1，2，3)未知，用RIV 法辨识出^(q－1)。然后计算R珋zi(k)，k = 0，1，2，可得

令

把有关估值代入到Ωi和δi中，可得(t)=。则由此可辨识出(t)、^(t)和(t)的值，另外计算算术平均可以得到融合估值^(t)和(t)。图1 为p1和在t 为从0 到10000 步的Matlab 仿真图，曲线表示估值，直线表示真实值。图2 为的局部估值(t)和融合估值(t)的仿真图，虚曲线表示局部估值，实曲线表示融合估值，直线表示真实值。可以看到两个图中，随着步数的增加，估值都逐渐收敛于真值，且图2 中的融合估值优于局部估值。构造估值偏差度函数选取500步、2000 步、5000 步、10000 步做出表2，可以看到随着步数的增加，在2000 步之后，估值已经稳定收敛于真值，特别是5000 步之后，大部分估值偏差度稳定在3%以内，所有估值稳定在偏差度5%以内，满足一定的实际要求。

图1 p1 的估值1

图2 的局部估值(t)，i = 1，2，3和融合估值(t)

表1 参数和噪声方差估值

表2 参数和噪声方差偏差度

4 结语

本文对带公共干扰白噪声，以及每个传感器的观测噪声均为有色噪声的多传感器系统，提出的一种多段辨识算法。用一个例子做了仿真说明。从例子中可以看出，对参数和噪声的估值收敛于真实值，且辨识的精度符合要求，辨识的目的已达到。

［1］ Ljung L.System Identification Theory for the User［J］.Second Edition.Prentice－Hall PTR，Beijing:Tsinghua University Press，1999，34(2):13－17.

［2］丁锋. 系统辨识(1):辨识导引［J］. 南京信息工程大学学报(自然科学版)，2011，3(1):1－22.

［3］马海军，林勇强. 系统辨识理论在建模中的应用［J］.大众科技，2010，5(4):50－51.

［4］ 王乐一，赵文虓. 系统辨识:新的模式、挑战及机遇［J］.自动化学报，2013，39(7):933－938.

［5］丁锋. 系统辨识(4):辅助模型辨识思想与方法［J］.南京信息工程大学学报(自然科学版)，2011，3(4):289－318.

［6］李娜，任一峰，赵敏. 基于Matlb 系统辨识的参数辨识与仿真［J］. 电子世界，2014，(3):199－200.

［7］何友，王国宏. 多传感器信息融合及应用［M］. 北京:电子工业出版社，2000.

［8］高媛. 多传感器系统模型参数和噪声统计的一种信息融合辨识方法［J］. 科学技术与工程，2009，9(17):4896.

［9］周曜. 非线性估计中无味滤波(UKF)与扩展卡尔曼滤波(EKF)之比较研究［J］. 宜春学院学报，2009，31(2):52－54.

［10］高媛，王伟玲，王强，等. 多传感器系统噪声统计辨识的一种相关方法［J］. 科学技术与工程，2009，9(1):1－15.

［11］徐慧勤. 在噪声环境下多传感器系统多段辨识算法研究［D］. 黑龙江大学，2010:4－5.

［12］邓自立，王欣，高媛. 建模与估计［M］. 科学出版社，2007.

［13］陈传璋. 数学分析［M］. 上海:上海科学技术出版社，1962.

［14］丁锋，谢新民. 线性多变量系统的联合辨识算法［J］.控制理论与应用，1992，9(5):545－550.

［15］王伟玲. 基于ARMA 新息模型的自校正信息融合估值器［D］. 黑龙江大学，2009:2－3.

［16］刘淑霞，黄敏.General 模型辅助变量辨识方法的研究［J］. 计算机工程与应用，2008，44(14):54－56.