均布荷载作用下地基的边缘沉降

刘紫红，王振辉

(1. 河南工业和信息化职业学院 建筑工程系，河南 焦作 454000;2. 河南理工大学 数学与信息科学学院，河南 焦作 454003)

客观地分析，地基土层承受上部建筑物的荷载，必然会产生变形，从而引起建筑物基础沉降。当地基在上部荷载作用下，产生严重沉降或不均匀沉降时，就会影响建筑物的正常使用，甚至发生整体倾斜、墙体开裂、基础断裂等事故。关于地基沉降的计算分析，已经有很多种方法。［1－9］

基于Boussinesq 地基模型，文献［9］研究了均布荷载作用下地基区域内部的沉降情况。事实上，在均布荷载作用下，受荷载区域的外部也会出现地基沉降，下面给出具体的沉降分析。

1 受荷载区域外部的沉降分析

为了计算上的方便，将受荷载地基理想化为矩形区域，边长分别为2a、2b。记地基土的变形模量是E0，泊松比是μ0，均布荷载p 作用于该矩形区域。

建立坐标系如图1 所示，原点O 位于矩形区域左边界的中点处，已知点H 是荷载外部的一点，为计算方便，假设点H 在坐标轴上，且距离右边界长度为d。

图1 点H 处的沉降分析Fig.1 The settlement analysis of the point H

结合图1 中点H 处的沉降分析示意图，利用元素分析法，在受均布荷载的矩形区域里选择一个小微元，不妨设微元的面积dxdy，则可以给出该微元上的荷载为pdxdy。由于此处可以将微元上的局部荷载近似为作用于一点处的集中荷载，因此该微元在点H 处的沉降位移可以表示为:

式(1)中，w 表示在整个均布荷载作用下点H 处的沉降位移。

记地基区域2a ×2b 为区域Ω，则点H 处的沉降位移为:

为了更好的计算上面的二重积分，选用极坐标系，不妨将极点选在点H 处，将地基区域放置于点H 的右边等距离的地方，如图2 所示。

图2 点H 处的沉降计算Fig.2 The settlement calculation of the point H

在图2 中，将区域Ω 在x 轴上方的部分记为区域Ω1，根据对称性，显然有

为了计算方便，将区域Ω1分解为两个区域Ω11和Ω12，根据二重积分的性质，有

在极坐标下，用不等式将区域Ω11和Ω12分别描述如下:

式(5)中，

结合式(5)，式(4)进一步可以写为:

将式(6)代入式(7)，经过较繁琐的计算可得:

将式(8)入式(3)及式(2)，可得点H 处的位移为:

由点H 的任意性可知，式(9)表示荷载区域外部水平线上的沉降情况。类似地，可以计算受荷载区域外部其它点处的沉降情况，此处不再赘述。

2 算例

已知地基上方形区域长2a =5m，宽2b =0.5m;地基土的变形模量E0=10MPa，泊松比μ0=0.35。方形区域上作用有均布荷载p = 200KN/m2，试分析该区域水平中心线上外部点处的地基沉陷情况。

依据文中分析，如图1 所示建立直角坐标系。记点H 处的地基沉降函数为f( )d ，利用文中推导的公式(9)，利用数学软件Mathematica 计算可得:

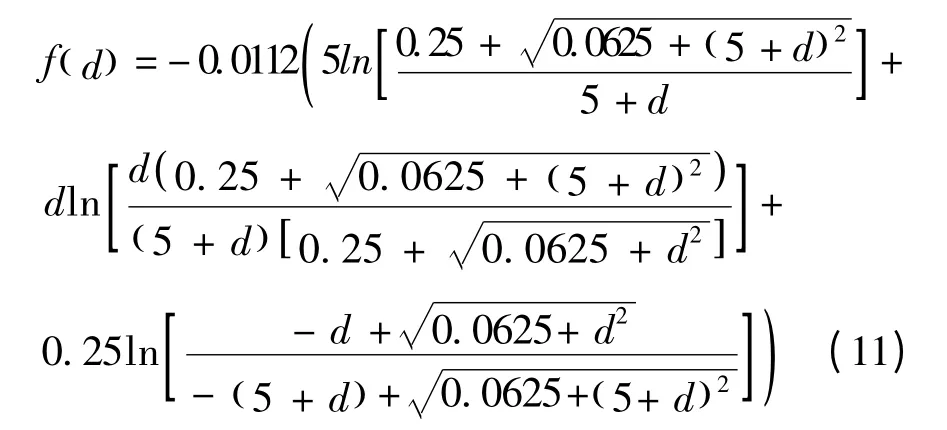
注:(1)结合点H 的任意性，将距离d 看作自变量，则函数f( )d 即为所求各点处的地基沉降函数;

(2)类似地，可以分析计算均布荷载作用下地基区域外部所有点的沉降情况，此处不再赘述。

为更好地体现算例中的沉降函数，编写Mathematica 程序，绘制函数f( )d 的图形如下:

图3 沉降函数的图形Fig.3 The graph of the settlement function

［1］陈国星，宰金珉. 弹性地基梁设计理论与方法［J］. 南京建筑工程学院学报，1998，46(3):42－48.

［2］王有凯，刘紫红，梁为民. 用最小势能原理求解半空间地基及地基梁问题［J］. 河南理工大学学报(自然科学版)，2011，30(4):462－466.

［3］阎盛海. 地下建筑结构中弹性地基直粱的初参数法［J］. 大连大学学报，2001，(2):9－18.

［4］周继凯，杜钦庆. 考虑水平力作用的改进型文克勒地基模型［J］. 河海大学学报，2004，32(6):669－673.

［5］马立博，时伟，周印章.Winkler 与三参数弹性地基梁模型的计算比较［J］. 青岛理工大学学报，2008，29(4):36－45.

［6］陈天愚，张克绪，单兴波. 弹性地基梁的修正刚度矩阵解法［J］. 哈尔滨建筑大学学报，2000，33(2):44－48.

［7］王国体，赖焕枫，胡志专，等. 双参数弹性地基梁有限差分法及变形、反力特征［J］. 合肥工业大学学报，2004，27(1):35－39.

［8］刘敏，贾丽红. 处理相邻建筑物地基沉降影响的方法［J］. 宜春学院学报，2003，25(6):46－47.

［9］刘紫红. 均布荷载作用下地基沉降的微元分析［J］. 河南科技，2014，5(上):66－67.