张弦梁结构刚度参数分析与优化设计

蒋友宝，黄星星

(长沙理工大学 土木与建筑学院，湖南 长沙410004)

0 引 言

张弦梁结构是一种用上弦拱构件和下弦索构件通过中间撑杆组合在一起的结构形式，见图1。日本的Saitoh 教授等［1-2］较早对该结构的受力基本原理进行了深入研究。随后，国内众多学者对张弦梁结构的受力性能开展了多方面研究。Wu［3］推导了张弦梁结构中撑杆屈曲临界荷载的计算公式，并研究了撑杆的稳定性能。吴祖咸等［4］对单向张弦梁结构的受力性能进行了较详尽的参数分析，得到了结构受力性能随各参数变化的规律。Chen 等［5］采用风洞试验、现场测试和数值模拟相结合的手段研究了某张弦梁(桁架)屋盖结构的抗风性能。赵宪忠等［6］和李刚等［7］对该结构张拉过程中整体刚度的变化过程进行了研究。赫成新和沈世钊［8］推导出了预应力张弦梁在张拉与加载阶段的平衡微分方程。刘开国［9］采用能量法进行了张弦梁结构的静力分析。

另外，苏旭霖等［10］采用瑞利-里兹法对预应力张弦梁结构的变形和内力进行了分析，并提出了一种上弦拱为圆弧线型的预应力张弦梁结构受力计算公式。最近，蒋友宝等［11-12］考虑索材料非线性，对不同失效模式下平面张弦梁结构受力全过程刚度变化规律进行了研究，结果表明在常用的参数(如高跨比等)取值范围内，上弦拱抗弯刚度对张弦梁结构整体刚度的贡献不大。

实际上对于大跨度钢结构，刚度设计一般起控制作用，因而基于刚度的优化设计引起了较多的重视［13］。上述这些研究为合理设计张弦梁结构提供了较好参考。但研究的深度还不够，如参数分析的范围较窄，基于刚度的参数分析与优化设计还较为欠缺等。

为此，采用有限元方法，以某张弦梁结构实例为基准模型，通过大范围地变化结构参数分析了该类结构使用阶段刚度变化的规律，在此基础上给出了优化设计的若干建议，为该类大型结构开展基于刚度的可靠度分析与设计提供参考。

图1 张弦梁结构示意图Fig.1 Diagram of beam string structure

1 张弦梁结构刚度分析方法

1.1 结构刚度计算

对于大型张弦梁结构，一般较难得到其刚度的解析解，此时多运用有限元方法来获得其数值解。

通过有限元分析选用ANSYS 软件。建模时上弦拱采用BEAM3 梁单元，撑杆采用LINK1 杆单元，下弦索因一般有较高的预应力水平，退拉的可能性较小，因而也采用LINK1 杆单元。当结构承受荷载F时，由有限元分析可得到结构跨中的挠度值ω，这样其对应的刚度K 可计算为

1.2 不考虑预应力的说明

需说明的是，此处的刚度是指张弦梁结构整体成形后使用阶段的刚度，此时结构整体刚度主要是由上弦和下弦按桁架受力形成的刚度来提供的，预应力对结构整体刚度的影响不大［12］，因而暂时不考虑预应力水平的影响。

1.3 分析方法对比

为了验证文中有限元方法模拟结果的准确性，以文献［10］中的两个张弦梁结构模型为算例，对比了本文方法与文献［10］方法的位移计算结果，见表1。其中施加的荷载按均布荷载2.35 kN/m 考虑。可知，两种方法的计算结果较为接近，两者的误差绝对值约为2%。由于文献［10］方法是依据瑞利-里兹法经理论推导得到的，具有较高的精度。这表明应用文中有限元方法来计算张弦梁结构的刚度，也将具有较高的精度。

表1 张弦梁模型位移分析结果对比Tab.1 Comparisons of displacement analysis results for beam string models

2 张弦梁结构刚度变化规律

2.1 基准模型说明

基准模型参照上海源深体育馆屋盖张弦梁结构的数据［14］，其跨度L=63 m，上弦箱形截面为540 mm×360 mm×18 mm×18 mm，钢材弹性模量为E1=2.06×105N/mm2，下弦钢索采用φ 5 mm×163，其弹性模量为E2=1.95×105N/mm2，撑杆截面面积采用上弦截面面积的一半，弹性模量与上弦拱相同，高跨比为1/10，支座形式为一端固定一端滑动铰支座。

相关研究表明影响张弦梁结构刚度的因素很多，但具有代表性的参数一般为:上弦抗弯刚度与下弦轴向刚度的比值α、上弦轴向刚度与下弦轴向刚度的比值β、高跨比f1和下弦索截面面积A2等，其中α和β 的计算公式为

其中:I 为上弦拱截面惯性矩，E1和E2分别为上弦拱和下弦索的弹性模量，A1和A2分别为上弦拱和下弦索的截面面积，L 为张弦梁结构的跨度。

蒋友宝等［12］对若干已建成张弦梁结构工程的结构参数进行了调查分析，表明α、f1和β 的常用取值范围分别为7.5×10-5～1.0×10-4、1/8 ～1/11 和5.11 ～11.5。上述基准模型对应的参数值分别为α=1.0×10-4、f1=1/10、β=9.72，恰在此常用取值范围内，因而具有较好的代表性。

2.2 α 的影响

在公式(2)中，令I=ir2A1，其中ir为上弦拱的截面回转半径，则式(2)可变为

其中:λr=L/ir可称之为名义长细比，因此通过名义长细比λr的变化可实现在其他参数保持不变时仅α发生改变。

考虑5 个不同的α 值，而其他参数与基准模型相同，对应的刚度计算结果见表2。可知当α 由7.5×10-5增至1.5×10-4时，其刚度由56.8 kN/m2增大到58.1 kN/m2，即结构刚度在原基础上仅增加了2.3%;而当α 增加至原来的16 倍时，其刚度由原来的56.8 kN/m2增大到71.0 kN/m2，增加了25%，提升效果较为有限。

表2 不同α 时刚度分析结果Tab.2 Stiffness analysis results with different values of α

2.3 f1的影响

因为α、β 和A2不随f1变化，所以仅改变结构的高跨比f1时其他的参数与基准模型相同。考虑f1取4个值，对应的刚度计算结果见表3。

表3 不同f1时的刚度分析结果Tab.3 Stiffness analysis results with different values of f1

由表3 可见，在常用的取值范围内，当高跨比由1/12 变到1/8 时，其刚度由40.6 kN/m2变为86.5 kN/m2，刚度增加了一倍多。可见增加结构的高跨比对结构整体刚度的提升效果较为明显。

2.4 β 的影响

由公式(3)知，若只改变结构的A1值，则能实现当β 变化时其他的参数与基准模型相同。考虑β 取5 个值变化，对应的刚度计算分析结果见表4。

表4 不同β 时的刚度分析结果Tab.4 Stiffness analysis results with different values of β

由表4 可见，β 由2.5 增到12.5 时，结构的刚度由45.6 kN/m2变到58.4 kN/m2，即结构的刚度仅增加了28.1%。相对于β 的变化幅度而言，刚度变化较小。可见仅增加上弦拱的截面面积A1，整体结构刚度提升较小。

2.5 A2的影响

由公式(2)、(3)知若A2变化时，欲保持α 和β 不变，则上弦拱的截面面积和惯性矩亦需同步变化。考虑下弦索截面面积A2取3 个值，其他的参数同基准模型参数，得到模型15、模型16 和模型17，对应的刚度计算分析结果见表5。

表5 不同A2索截面面积时刚度分析结果Tab.5 Stiffness Analysis results with different cable cross-sectional area A2

由表5 可见，当索的面积由1 600.3 mm2增至6 401.0 mm2时，即面积增加为原来的4 倍时，结构的刚度将由28.6 kN/m2增大到114.6 kN/m2，亦为原来的4 倍，呈现出同步变化的现象。原因主要是此时上弦拱的截面面积和惯性矩亦为原来的4 倍。这说明当α、β 和f1一定时，结构整体刚度与下弦索面积成正比。

3 刚度参数分析

3.1 特征参数取值

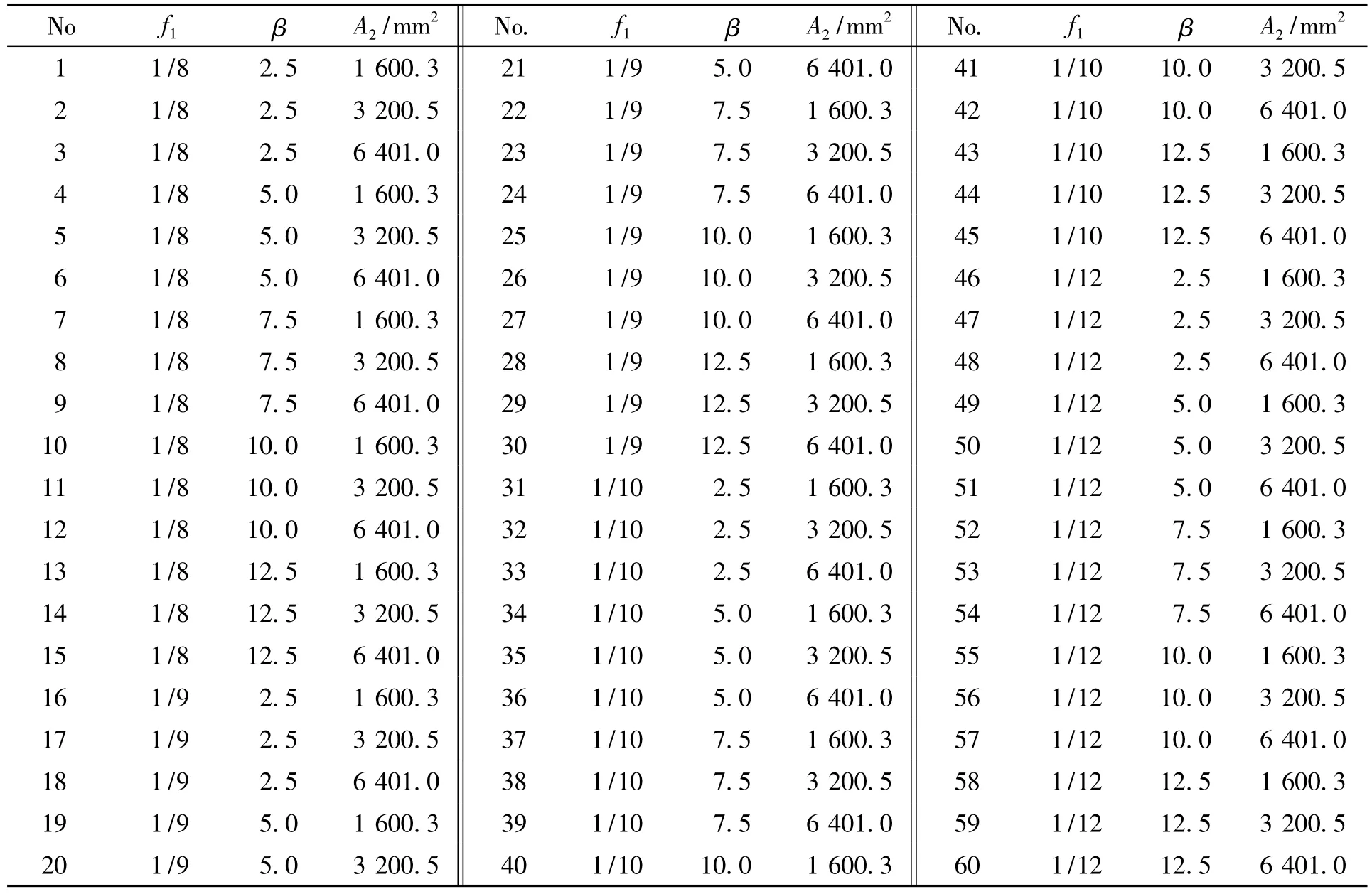
上文分析结构刚度变化规律时仅考虑了单变量因素的影响，其余变量因素同基准模型。此处考虑多变量因素的影响，进行大范围的参数分析。仍考虑α 取5 个值，f1取4 个值，β 取5 个值，A2取3 个值，最终各参数取值结果如表6 所示。

表6 特征参数取值Tab.6 Values of characteristic parameters

另外，在结构高跨比一定时，上弦拱的矢高和下弦索的垂度可能并不相同。因此，以下考虑两种情形:上弦拱矢跨比fa和下弦索垂跨比fc相同，均为0.5 f1(Case A);上弦拱的矢跨比为0.65 f1，下弦索的垂跨比为0.35 f1(Case B)。具体见表7。

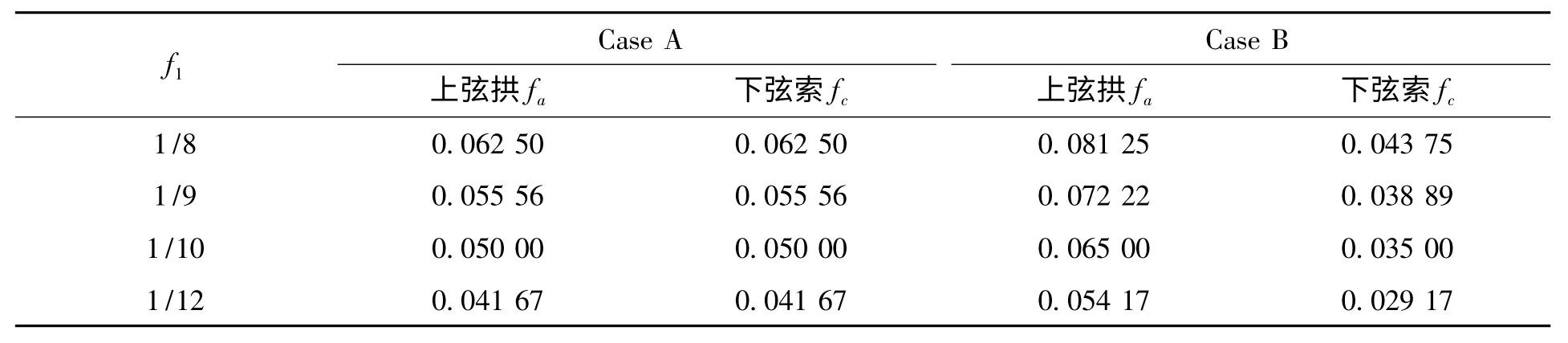
表7 上弦拱矢跨比和下弦索垂跨比取值Tab.7 Rise-to-span ratios of arch and sag-to-span ratios of cable

根据表6，可知Case A、B 各分别总共有300 种组合情形;而对应每种α 取值下则有60 种组合情形，组合种类编号为No.1 ～No.60，如附表1 所示。

3.2 总体分析结果

根据有限元分析可得到各组合情形下的挠度ω，然后按公式(1)得到Case A、B 各300 种情况下的刚度K。定义一刚度比值ζ，其计算式为

其中:K 为各种情况下的刚度，K0为基准模型刚度。

3.3 结果讨论

ζ 分析结果如图2 所示。从图2(a)、(b)可知，每个α 值对应的ζ 曲线较为相似，都呈现一定规律性的变化，即在f1和β 参数不变下，ζ 随A2增大而增大。如No.1、No.2 和No.3 这一组，No.4、No.5 和No.6 这组等。在其他参数相同情形下，ζ 值随α 值的增大而增大。图2(a)中ζ 最大值约为3.48，出现在α 取0.001 2时的No.15 情形;ζ 最小值约为0.28，出现在α 取0.000 075 时，No.46 情形。图2(b)中ζ 最大值约为3.42，亦出现在α 取0.001 2 时的No.15 情形;ζ 最小值约为0.27，亦出现在α 取0.000 075时，No.46 情形。

从图2(a)、2(b)中还可以看出，当结构高跨比一定时，Case A(较大下弦索垂跨比)对应的ζ 值与相同情形下Case B(较小下弦索垂跨比)对应的ζ 值较为接近，但前者要稍高一些，最大可高出约3%。

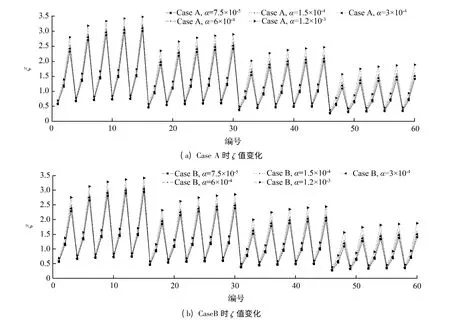
图2 不同情形下ζ 值变化Fig.2 Values of ζ for different cases

4 优化设计

4.1 优化设计准则和分析

在实际设计张弦梁结构时，用钢量是衡量设计合理性的重要指标之一。为了更好的指导实际工程，需知道各组合情形下结构刚度与质量的比值大小。定义一无量纲化的刚质比参数λ，即为各情形下刚度K 与质量M 的比值除以基准模型的刚质比，计算式为

其中:质量可由各杆件质量的累加求和得到，而各杆件质量则为密度ρ、杆件长度L 和杆件截面面积的乘积。

由附表1 设计参数取值计算出各组合下的刚度，然后再除以各自组合下的质量，可得到各种情形下对应的λ 值，如图3。

4.2 设计讨论

对比图3(a)、(b)可知，当结构高跨比在1/12 ～1/8 范围内取一定值时，即上弦拱矢跨比和下弦索垂跨比之和在此范围内取定值时，增加下弦索垂跨比，则结构的刚质比λ 也略有增加。文献［15］的研究结果曾表明，增加下弦索垂跨比对张弦梁结构的承载能力亦有较大改善。因此综合考虑，较大的下弦索垂跨比对刚度和承载能力这两方面均较为有利。

由图3(a)知，λ 的最大值约为4.22，出现在α 取0.001 2 时的No.1 ～No.3 情形。这3 种情形的β和f1值相同而仅下弦索面积不同，原因主要是当α、β 和f1一定时，结构整体刚度与下弦索面积(结构质量)成正比;此时，β 和f1分别为文中参数分析范围内β 的最小值和f1的最大值。另外，λ 的最小值约为0.56，出现在α 取0.000 075 时的No.58 ～No.60 情形，此时β 和f1分别为文中参数分析范围内β 的最大值和f1的最小值。由图3(b)知，λ 的最大值约为4.15，出现在α 取0.001 2 时的No.1 ～No.3 情形;λ的最小值约为0.56，出现在α 取0.000 075 时的No.58 ～No.60 情形。这与图3(a)反映的变化规律类似。

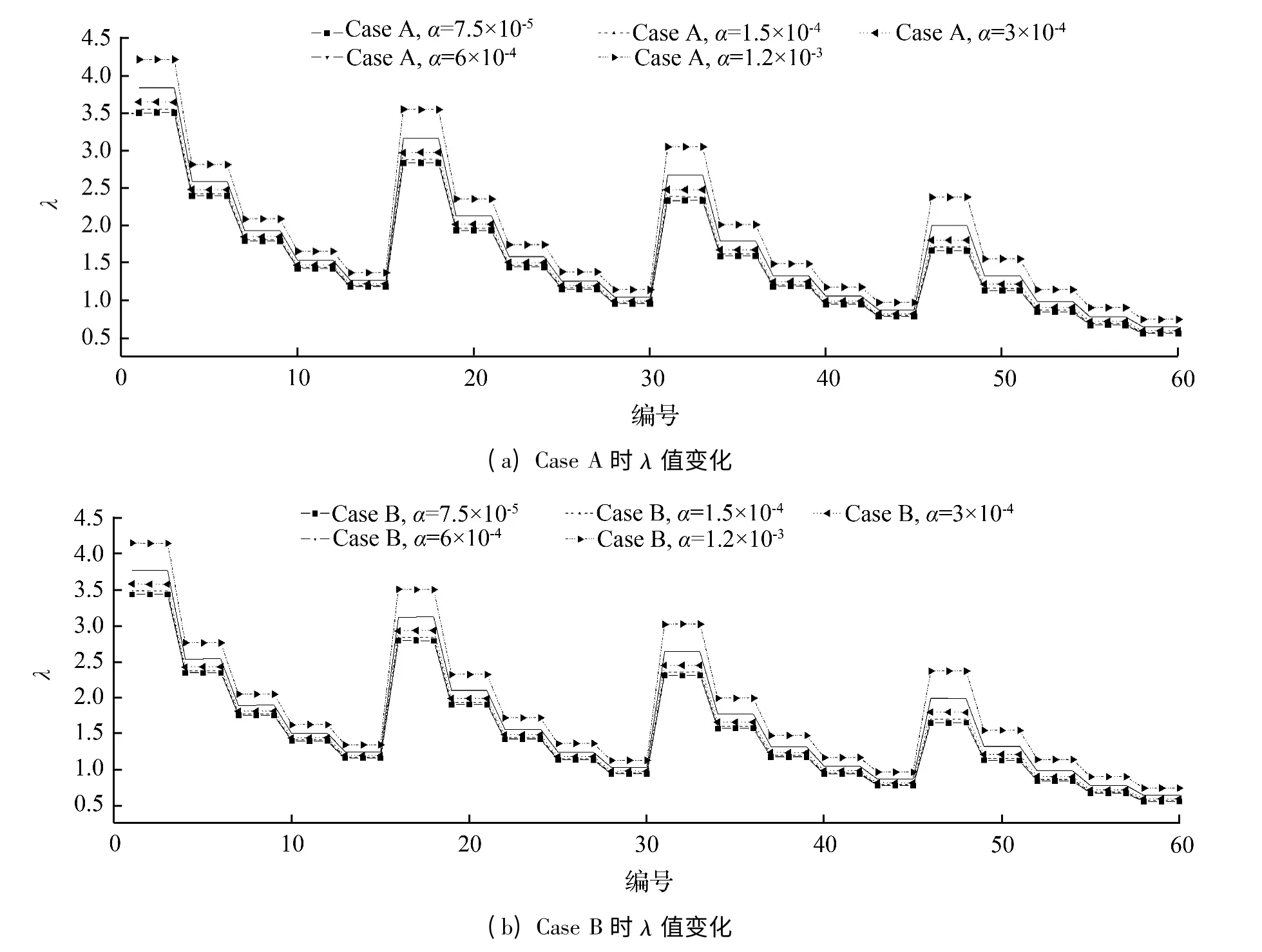
图3 不同情形下λ 值变化Fig.3 Values of λ for different cases

这说明在实际设计张弦梁结构时，从刚度和用钢量两方面综合考虑，应尽可能选用较大的结构高跨比、索垂跨比和较小的上弦轴向刚度与下弦轴向刚度比值。

5 结 论

①在高跨比、上弦轴向刚度与下弦轴向刚度比值和上弦长细比一定时，张弦梁结构刚度近似与下弦索面积成正比。

②当结构高跨比在1/12 ～1/8 范围内取一定值时，增加下弦索垂度，则结构的刚质比也略有增加。

③在文中参数分析范围内，当对张弦梁结构刚度进行优化设计时，应尽可能选用较大的结构高跨比、索垂跨比和较小的上弦轴向刚度与下弦轴向刚度比值。

［1］ SAITOH M，OKADA A，MAEJIMA K.Study on mechanical characteristics of a light-weight complex structure composed of a membrane and a beam string structure［C］//ABEL J F，LEONARD J W，PENALBA C U.Proceedings of the IASSASCE International Symposium on Spatial，Lattice and Tension Structures.Atlanta，Georgia，USA:American Society of Civil Engineers，1994:633-641.

［2］ SAITOH M，OKADA A.The role of string in hybrid string structure［J］.Engineering Structures，1999，21(8):756-769.

［3］ WU M.Analytical method for the lateral buckling of the struts in beam string structures［J］.Engineering Structures，2008，21(8):2301-2310.

［4］ 吴祖咸，楼文娟，高子珺.单向张弦梁结构的受力性能研究［J］.钢结构，2010，25(7):1-3，18.

［5］ CHEN F B，LI Q S，WU J，et al.Wind effects on a long-span beam string roof structure:Wind tunnel test，field measurement and numerical analysis［J］.Journal of Construction Steel Research，2011，67(10):1591-1604.

［6］ 赵宪忠，陈建兴，陈以一.张弦梁结构张拉过程中的结构性能试验研究［J］.建筑结构学报，2007，28(4):1-7，50.

［7］ 李刚，冯大斌，梁存之.张弦梁张拉成型控制方式研究［J］.施工技术，2010，39(8):170-172.

［8］ 郝成新，沈世钊.平面预应力索-拱体系［J］.哈尔滨建筑工程学院学报，1986，19(3):1-15.

［9］ 刘开国.大跨度张弦梁式结构的分析［J］.空间结构，2001，7(2):40-43.

［10］苏旭霖，刘晟，薛伟辰.基于瑞利-里兹法的预应力张弦梁变形与内力分析［J］.空间结构，2009，15(1):49-54，96.

［11］蒋友宝，郑晶，李江，等.索材料非线性对平面张弦梁结构承载性能的影响分析［J］.工程建设，2011，43(3):8-10，35.

［12］蒋友宝，李耀，杨伟军.不同失效模式下平面张弦梁结构受力全过程刚度变化［J］.中南大学学报:自然科学版，2013，44(7):3006-3013.

［13］杜文风，田永轩.大跨静定桁架满位移最小重量设计系数分配法［J］.广西大学学报:自然科学版，2010，35(4):627-632.

［14］薛伟辰，刘晟，苏旭霖，等.上海源深体育馆预应力张弦梁优化设计与试验研究［J］.建筑结构学报，2008，29(1):16-23.

［15］蒋友宝，冯健，蒋剑锋，等.影响张弦梁结构若干参数对承载性能的影响分析［J］.工业建筑，2008，38(1):103-105.

附表1 设计参数取值表Appendix Tab.1 Values of design parameters