粒子群－神经网络在华南夏季降水短期气候预测中应用研究

覃卫坚，李耀先，陈思蓉，谢敏

（1．广西区气候中心，广西 南宁 530022；2．广西气象减灾研究所，广西 南宁 530022）

引言

华南是我国降水最多的地区之一，每年因强降水引发的洪涝灾害都会给当地造成严重的经济损失和人员伤亡。近年来华南降水引起专家的关注，肖伟军等［1］分析了华南夏季降水时空分布特征；张婷［2］研究了华南雨带变化与马斯克林高压和澳大利亚高压的关系；郑彬等［3］、苗春生等［4］、邓立平等［5］分别研究了华南降水异常与南海夏季风、东北冷涡、海温的关系。动力气候模式预测是现代气候预测技术的发展方向，目前动力模式预测水平还不高，利用各种异常因子及其前兆信号来做预测，无疑是提高短期气候预测的有效途径［6－8］。 如封国林等［9］结合海温、环流等前期异常信号分析了2011年长江中下游地区旱涝急转成因；杨杰等［10］、熊开国等［11］研究了多因子异常组合的多元客观相似，提出动力统计模式预报误差的订正方法。粒子群－神经网络是最近流行的一种预测方法，它具有处理非线性问题的能力，比传统统计方法更具有优势。本研究查找华南夏季降水的影响关键因子，利用这些因子和粒子群－神经网络建模做预报，尤其分析关键因子出现异常时对华南降水的影响，在关键因子异常年份里利用这些因子建模预测，提高华南夏季降水预测技巧。

1 资料与方法

1．1 资料

降水资料使用1961～2013年广东、广西、海南三省共110个气象观测站的20：00～20：00的日降水资料、美国气候预测中心组合降水分析（CMAP）资料。指数资料来源于中国国家气候中心（NCC）的74项环流特征量和海温指数、美国国家海洋和大气管理局 （NOAA）的40项海洋和环流指数资料。1961～2013年NCEP／NCAR高度场和风场再分析资料。文中前期关键因子均由以上各指数和再分析资料计算产生。

组合因子定义为：当预报量与再分析资料的相关场中存在两个相邻的、符号相反的高相关区，将这两个区域格点资料的平均值相减，做为组合预报因子［12］。模式资料使用国家气候中心第二代海－陆－冰－气耦合的气候系统动力模式生成的1983－2013年共31a夏季（6－8月）降水的回报资料。降水距平百分率超过20%定义为异常降水。

1．2 经验正交函数方法（EOF）

本文利用EOF方法对华南夏季（JJA）降水变化的空间分布结构进行分析。EOF方法把降水场资料矩阵mXn分解为mXn=mVmmZn，其中mVm是空间函数，而mZn则是时间系数矩阵，m为站点数，n为年数。利用各模态的时间系数序列来做预报，各模态时间系数预报值和特征向量空间场组合，就得到夏季降水的预报，以下各种预报检验结果均已转换为降水量。

1．3 粒子群－神经网络方法

神经网络近年来兴起的一种具有解决非线性问题的统计方法，通常的神经网络在计算中经常出现网络因振荡不能收敛等问题，而最新流行的粒子群算法（Particle Swarm Optimization，PSO）具有全局搜索的特性，其通过个体之间的互动协作来搜寻全局最优解，优化了神经网络的连接权和网络结构，克服了以往神经网络计算中的问题［13－15］。粒子群算法是Kennedy等［16］在1995年最早提出的一种基于群体智能方法的计算技术。粒子群－神经网络模型的具体建模步骤［17－18］如下：

（1）初始化粒子群。

（2）计算每个粒子的适应度。

（3）随机输入个体最佳初始值及全局最佳初始值，再根据粒子的适应度进行更新。

（4）使用权重系数矩阵控制着网络权值和阀值的大小。

（5）连接结构矩阵变量矩阵控制着隐节点数，计算更新位置矩阵中的连接结构矩阵。

（6）反复进行（2）～（5）步骤的计算，当迭代次数达到了最大训练次数或满足最小训练误差时，停止计算，并输出最优解。通过解码得到n个神经网络模型的结构和网络连接权，再经过网络训练得到了n个神经网络预报模型，输入建模样本和独立样本进行预报，把这些神经网络个体预报值的平均值作为粒子群－神经网络集合预报模型的预报值［20］。

1．4 异常信号的选取

计算标准偏差：

使用计算标准偏差来判断某个因子是否异常，当因子强度距平值的绝对值大于2σ时，则定义该因子为异常。

2 华南夏季（JJA）降水EOF分析

华南地区面积广阔，天气形势多样，因此有必要使用EOF方法来分析华南夏季降水变化的空间分布结构，EOF方法分解出的特征向量正好能够反映出降水变化的空间结构，分解出来的这些模态，按特征值大小排列，第一模态最能代表近50a的华南夏季降水量变化特征的分布场，其次为第二模态、第三模态等，华南夏季降水的前两个模态累计贡献率达到了48%。

EOF第一模态分布如图1a所示，整个华南地区第一模态的特征向量值除了海南西南部为正值外，其余地区为负值，方差贡献率达36．5%。这说明了华南大部降水变化一致性特征为主要降水特征，原因可能为华南大部共同受大尺度天气系统造成该地区同时涝或旱。图中还可以看出第一模态最大的负信号出现在广西的中东部和广东的北部，该区域为降水变化敏感区，即降水变化比较大。由图1b为第一模态时间系数历年值，从整体来看时间系数有减小趋势，即华南大部夏季降水有增加趋势，但趋势不明显。年代际变化来看，60－70年代为波动期；80年代时间系数为正值期，即华南大部降水偏少期；90－10年代时间系数为负值期，即华南大部降水偏多期。

图1 华南夏季（JJA）降水EOF分析第一模态的空间分布（a）和时间系数（b）

3 预报建模及试验对比分析

3．1 查找气候影响因子

由于篇幅有限且第一特征向量具有较大的贡献率，以下只分析第一特征向量，把第一特征向量的时间系数作为预报量。为了查找降水模态的影响关键因子，首先计算了第一特征向量时间系数与前期各月中国国家气候中心74项环流特征量和海温指数、NOAA 40项海洋和环流指数资料的相关系数；再统计了其与NCEP／NCAR各层高度及风场的相关系数，查找高相关的关键区域。通过统计和筛选得到第一特征向量时间系数的关键因子共27个（相关通过了5%水平的显著性检验），并作为预报因子。相关情况如表1所示，从表中可以看出NCEP／NCAR各层高度及风场的高相关区域整理出来的关键因子的相关系数最高，均在0．43以上，其中前一年4月日本东部洋面和东西伯利亚海500hPa高度场之差的相关系数最高，达到0．57；与国家气候中心74项指数及NOAA 40项指数的相关系数在 0．35—0．49之间。说明了华南夏季降水高相关关键区因子并非常规统计的环流和海温指数，而是跟组合因子相关最大，在相关系数最高的前5个因子中有3个是组合因子。

在查找影响因子过程中不但参考了相关程度，还考虑了这些因子对华南夏季降水的动力学机理。正如黄嘉佑等［21］研究指出前期冬季极涡和副高对中国夏季降水有着重要影响；王黎娟等［22］指出华南大范围持续暴雨期间西太平洋副高异常偏西偏南，且强度偏强；林爱兰等［23］指出华南持续性暴雨是各类中高纬度环流系统稳定维持与热带水汽输送共同作用的结果。因此在影响的天气系统中选择了对华南水汽输送有重要影响的副热带高压的各项指数、影响南下冷空气的极涡系统、影响南亚季风发生发展的印度洋海温偶极子，筛选出来这方面的因子为表1中的第1～16个因子。查找高相关的关键区时重点考虑亚洲附近区域，尤其是中国及周边地区的高相关区，如日本东部洋面和东西伯利亚海500hPa高度场之差（相关系数为 0．57）、北太平洋（120E－160W）南北向 700hPa U风场差（相关系数为 0．52）、东太平洋（30－50N）与阿拉斯加700hPa U风场差（相关系数为 0．49）、哈萨克斯坦和乌拉尔山脉北部700hPa U风场差（相关系数为0．43）等反映了中高纬度环流的反位相关系，反映出了大气的经向环流情况；维多利亚岛到巴芬海区域的500hPa高度场与夏季降水的相关系数也达到了－0．52，该区域位于北美洲的北部，跟极涡关系密切；印度东部700hPa U风场（相关系数为0．5）反映出了过赤道气流向东传播的程度，有利于水汽向华南输送。高相关的关键区因子为表中的第17～27个因子。

表1 EOF分析第一特征向量的时间系数与各预报因子的相关系数

3．2 逐步回归预测

逐步回归方法在气候预测中是经常被使用的一种方法，下面利用与华南夏季降水EOF第一特征向量时间系数相关显著的27个关键因子，采用逐步回归方法建立预测方程，建模拟合取1961－2004年43a预测样本，采用不同的F值逐步回归方法从前面因子群里进行关键因子再提取，以F＝2，F＝4两种不同F值建立第一特征向量时间系数的逐步回归预报方程：

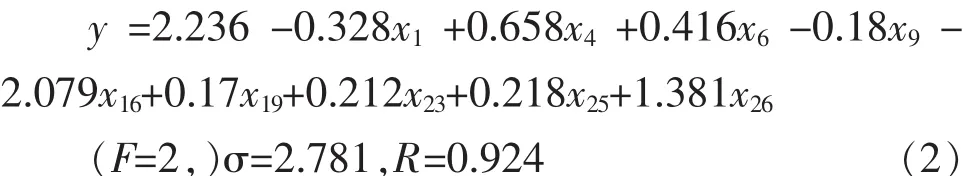
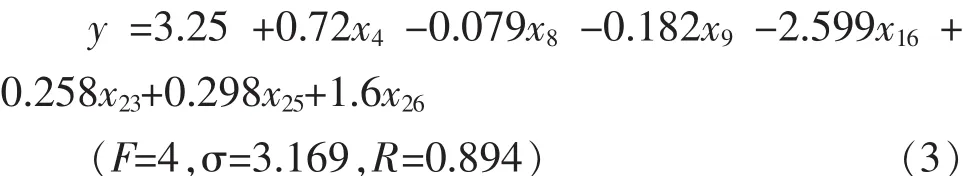
利用以上两个方程对2004－2013年10a进行独立样本预测，把每年前期因子的实况值代入以上预报方程即可得到预报值。从预测结果和实况对比来看，（3）方程绝对误差和相对误差均比（2）方程小，因此采用（3）来做预报实验，把前期因子的值代入方程计算得到时间系数值，通过时间系数和特征向量相积转换成降水量预报值，降水的预报值如表2所示，平均绝对误差为101．5mm，平均相对误差为15．8%。华南夏季降水1981－2010年30a平均值为742．6mm，从预测和实况的距平来看，预测和实况距平符号一致的有一半年份，预测同号率仅为50%。

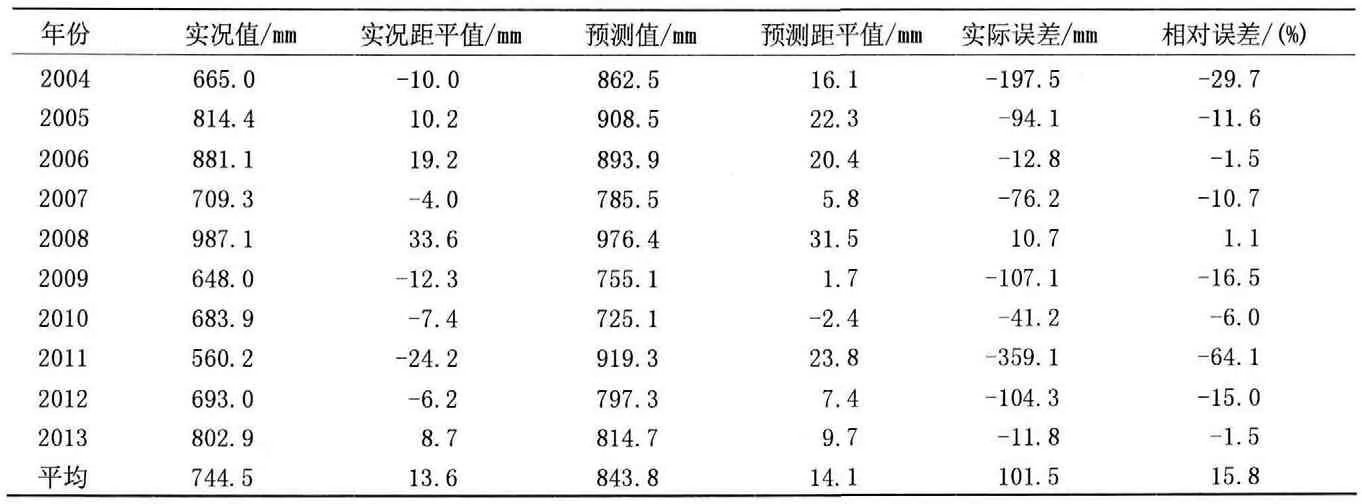
表2 2004－2013年逐步回归方程的预测检验结果

3．3 NCC＿CSM 模式预测

国家气候中心NCC＿CSM模式近10a回报结果如表3，平均绝对误差为98．3 mm，平均相对误差为13．3%，从预报效果来看，模式预报的相对误差和绝对误差均比逐步回归方法小，预报能力比传统方法有所提高。但模式预报结果的距平值平均仅为2．7%，远低于实况10a平均距平值13．6%，而逐步回归10a预报平均距平值更接近实况平均距平值，模式预报降水量很接近气候平均值，基本无法预报异常降水。

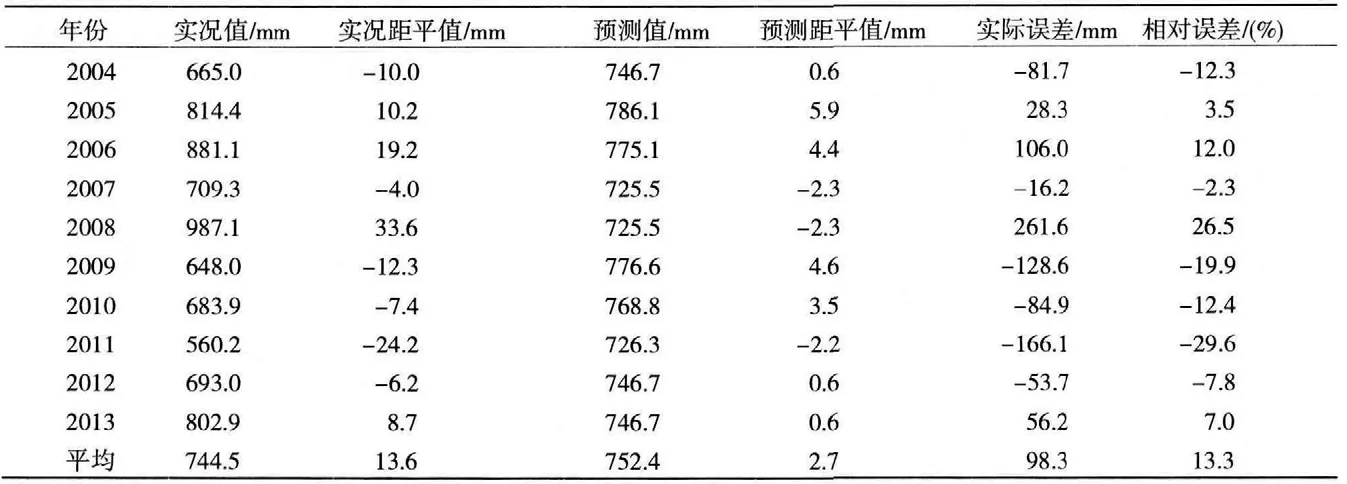
表3 2004－2013年NCC＿CSM模式的预测检验结果

3．4 粒子群－神经网络建模预测

采用不同的F值逐步回归方法从27个关键因子群里再进行因子提取，计算得到的关键因子建立神经网络预报模型，两个不同F值得到不同因子数的两个方程，其中利用方程（8）得到的关键因子来做的神经网络预测效果最好，因此下面采用（8）方程中因子做预报。预报模型的建模样本个数为43，预报因子个数为7个，设定粒子位置的上限为5（下限为－5），隐节点为输入节点倍数上限为1．9（下限为0．3），学习因子为 0．5，训练次数为 200，总体误差为 0．01。粒子群－神经网络预报模型对2004－2013年10个独立样本进行预报检验，从预报结果来看 （如表4），10a绝对误差平均为 85．6mm，相对误差为 13．2%，绝对误差和相对误差均小于逐步回归和模式预报，预测的同号率与逐步回归、模式预报相同，均为50%。神经网络10a预报平均距平值为10．6%，接近实况平均距平。尤其异常偏多年2008年预报准确，在异常降水预报方面比气候模式预报有优势。

表4 2004－2013年粒子群－神经网络建模预测检验结果

4 异常降水年份的预报试验

从3．3节分析可见国家气候中心的气候系统动力模式预报技巧并不高，尤其异常降水基本无法预报，因此模式预报有很大的提高空间。在动力模式预报技巧还不高的情况下，我们如何利用统计方法能真正抓住一些有预报技巧的现象呢？这值得我们探讨。通常认为，在异常降水出现时前期应该出现与之相关联的某区域环流异常现象，如1994年华南夏季降水异常偏多，平均较常年同期偏多5成，当年在27 个因子里有 5 个 （x8、x13、x20、x22、x25） 出现异常；1989年华南夏季降水异常偏少约4成，当年有5个因子（x2、x5、x24、x25、x26）出现了异常；其他异常年份也有1－4个因子出现异常。由此可见，通过相关显著的这些异常因子对华南夏季异常降水有着重要的影响。因此可以利用这些异常因子来做降水气候预测，下面结合具有处理非线性问题能力的粒子群－神经网络，使用这些因子异常状况来建模做预报试验。

在计算得到的27个关键因子中，查找它们出现异常的年份以及降水同时发生异常的年份。在降水出现异常的年份里，使用当年出现异常的因子建模，以当年以前的年份作为预测样本，当年降水量做为预报对象。从7年降水异常年份的回报计算来看（如表5），异常关键因子的粒子群－神经网络建模预报，预报和实况的同号率达到85．7%，而动力模式预报同号率仅为57.1%，远低于异常关键因子神经网络建模预报。7a异常关键因子建模预报的平均绝对误差为159．3mm，远小于动力模式误差218.6mm；相对误差为22．6%，而动力模式预报相对误差为29．4%。由此可见，由于粒子群－神经网络既具有强大的结构性知识表达能力，又具有自身参数调整优化的能力，而降水过程受大气运动的热力、动力、水汽条件因素的影响，具有明显的非线性变化特征，因此在因子异常年份里利用具有处理非线性问题能力的粒子群－神经网络建模预测具有很好的预测效果，具有很好的应用前景。

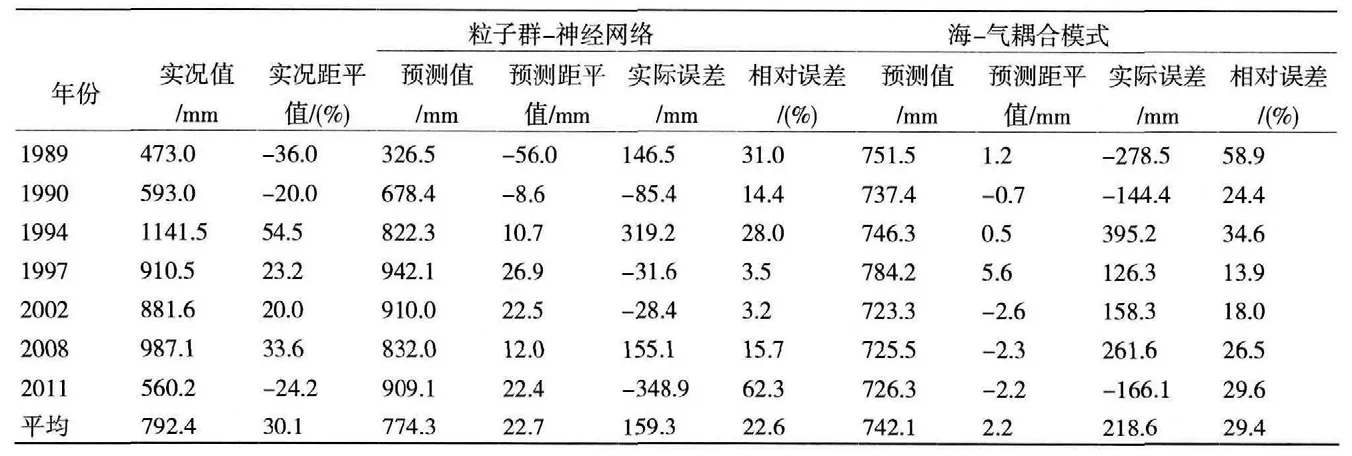
表5 降水异常年份的异常关键因子粒子群－神经网络建模和动力模式预测结果比较

5 结论与讨论

通过分析得到一下结论：

（1）从近10年回报试验来看，动力模式预报和粒子群－神经网络10a预报平均绝对误差分别为98．3mm、85．6mm， 平 均 相 对 误 差 分 别 为 13．3%、13．2%，而逐步回归方法平均绝对误差为101．5mm，平均相对误差为15．8%。总之，粒子群－神经网络预报略好于模式，模式又好于逐步回归方法。

（2）从异常年份的预报试验来看，异常关键因子的粒子群－神经网络建模预报的同号率高达到85．7%，远高于动力模式预报的57.1%；异常因子神经网络预报的平均绝对和相对误差分别为159．3mm、22．6%， 小 于 动 力 模 式 的 218.6mm 和29．4%。由此可见，利用异常关键因子的粒子群－神经网络建模预测效果好于动力模式预报。

［1］肖伟军，陈炳洪，刘云香．近45a华南夏季降水时空演变特征 ［J］ ．气象研究与应用， 2011， 30 （1）： 12－14．

［2］郑彬，施能．南海夏季风对华南夏季降水年代际变化的影响 ［J］ ．南京气象学院学报，2006，29（4）：477－482．

［3］张婷，魏凤英，韩雪．华南汛期降水与南半球关键系统低频演变特征 ［J］ ．应用气象学报，2011，22（3）：265－273．

［4］苗春生，吴志伟，何金海等．近50年东北冷涡异常特征及其与前汛期华南降水的关系分析 ［J］．大气科学，2006， 30 （6）： 1249－1256．

［5］邓立平，王谦谦．华南前汛期 （4－6月）降水异常特征及其与我国近海海温的关系 ［J］．热带气象学报，2002， 18 （1）： 45－55．

［6］丁一汇．季节气候预测的进展和前景 ［J］．气象科技进展， 2011， 1 （3）： 14－26．

［7］穆穆，陈博宇，周菲凡等．气象预报的方法与不确定［J］ ．气象， 2007， 37 （1）： 1－13．

［8］魏凤英．我国短期气候预测的物理基础及其预测思路［J］ ．应用气象学报， 2011， 22 （1）： 1－11．

［9］封国林，杨涵洧，张世轩等．2011年春末夏初长江中下游旱涝急转成因初探 ［J］．大气科学，2012，36（5）：1009－1026．

［10］杨杰，王启光，支蓉等．动态最优多因子组合的华北汛期降水模式误差估计及预报 ［J］．物理学报，2011， 60 （2）： 029204－1－13．

［11］熊开国，赵俊虎，封国林等．汛期降水相似动力预报－模式误差主分量相似预报方法 ［J］．物理学报，2012， 61 （14）： 149204－1－11．

［12］农吉夫，金龙，谭福锦，等．最优组合预测的短期气候预报建模研究 ［J］．数学的实践与认识，2008，38（8）： 91－97．

［13］金龙，陈宁，林振山．基于人工神经网络的集成预报方法研究和比较 ［J］ ．气象学报， 1999， 57（2）： 198－207．

［14］吴建生，金龙，汪灵枝．遗传算法进化设计神经网具网络气象预报建模研究 ［J］．热带气象学报，2006，22（4）： 411－416．

［15］金龙，罗莹，王业宏，等．月降水量的神经网络混合预报模型研究 ［J］ ．高原气象， 2003， 22 （6）： 618－623．

［16］ Kennedy J， Eberhart R C．Particle Swarm Optimization［A］ ．In： Proc IEEE International Conference on Neural Networks ［C］ ．IV Piscataway， NJ： IEEE Service Center， 1995， 1942－1948．

［17］ Hua－sheng Zhao， Long Jin and Ying Huang．An Objective Prediction Model for Typhoon Rainstorm Using Particle Swarm Optimization－Neural Network Ensemble ［J］ ．Natural Hazards．2014， 73 （2）：427－437．

［18］吴建生．基于粒子群算法的神经网络短期降水预报建模研究 ［J］ ．智能系统学报， 2006， 1 （2）： 67－73．

［19］吴建生，刘丽萍，金龙．粒子群－神经网络集成学习算法气象预报建模研究 ［J］．热带气象学报，2008，24（6）： 679－686．

［20］黄颖，金龙，黄小燕，等．基于局部线性嵌入的人工智能台风强度集合预报模型 ［J］ ．气象，2014，40（7）： 806－815．

［21］黄嘉佑，刘舸，赵昕奕．副高、极涡因子对我国夏季降水的影响 ［J］ ．大气科学， 2014， 28（4）： 517－526．

［22］王黎娟，陈璇，管兆勇，等．我国南方洪涝暴雨期西太平洋副高短期位置变异的特点及成因［J］．大气科学，2009， 33 （5）： 1047－1057．

［23］林爱兰，李春晖，郑彬，等．广东前汛期持续性暴雨的变化特征及其环流形势 ［J］．气象学报，2013，71（4）： 628－642．