混凝土CS 和D 双时变下氯离子浓度分布解析解

元 野，杨绿峰，2，周 明

(1.广西大学 土木建筑工程学院，工程防灾与结构安全教育部重点实验室，广西 南宁530004;2.广西壮族自治区住房和城乡建设厅，广西 南宁530028)

0 引 言

在高速铁路、跨江海大型桥梁和海港码头等基础设施建设中所出现的混凝土中钢筋的锈蚀问题已引起混凝土科学与工程界的高度重视，而氯离子正是引起钢筋锈蚀最主要的原因［1］。钢筋锈蚀导致钢筋有效受力截面缩小，混凝土保护层出现裂缝，这大大缩短结构工作寿命，危害结构承载力和安全性。因此，正确选取混凝土中氯离子扩散模型及参数表达形式，并据此分析混凝土中氯离子扩散过程和分布规律，这是进行结构耐久性设计的关键，具有重要的工程意义和学术研究价值。

目前，学术界和工程界普遍使用Fick 第二定律［2］描述氯离子扩散过程，并假设混凝土表面氯离子浓度为恒定值，建立氯离子分布函数的求解方法，进而分析结构的耐久性及服役寿命。然而，研究表明，处于氯盐环境下的真实混凝土结构，其表面氯离子浓度并不是恒定值。赵羽习等［3］检测实际工程混凝土中氯离子浓度拟合时发现，混凝土表面氯离子浓度随时间逐步积累升高，并最终达到一个稳定值。王命平等［4］建立了盐雾区混凝土结构表面氯离子浓度随时间变化的分段线性模型;Petcherdchoo［5］利用暴露试验数据和平方根模型拟合了随时间变化的表面氯离子浓度;Cost 等［6］通过对试验数据拟合，得到不同环境作用区域表面氯离子浓度的幂函数模型;Song 等［7］提出利用表面氯离子浓度的对数模型拟合实验结果效果较好;Kassir 等［8］应用指数模型来描述表面氯离子浓度的时变性。余红发等［9］引入表面氯离子浓度指数模型，推导出表面氯离子浓度时变的一维扩散解析解。Ann 等［10］求解了表面氯离子浓度为线性模型和平方根模型的氯离子扩散解析解，并比较了不同表面氯离子浓度模型对氯离子扩散过程的影响，并发现这种影响可能使预测的混凝土服役寿命相差2 ～3 倍。上述研究表明，混凝土表面氯离子浓度时变性对混凝土中氯离子的扩散过程和浓度分布规律有显著影响。

由于混凝土的氯离子扩散系数属于材料参数，当水化龄期增加时，混凝土抗氯离子渗透能力逐渐增强［11］。Takewake 等［12］通过实验研究了扩散系数随混凝土暴露时间而发生变化的规律，提出了扩散系数衰减经验模型。Mangat 等［13］提出了扩散系数幂函数衰减经验模型，并据此研究了混凝土中氯离子的浓度分布。Maage 等［14］通过分析在役混凝土检测数据和实验室试验数据，提出了扩散系数的幂函数时变模型。Song 等［15］研究认为应该引入时变扩散系数修正氯离子扩散控制方程，据此得到正确的氯离子扩散解析解。Tang 等［16］详细分析了扩散系数时变条件下由于解析解简化推导造成的误差，给出了不同扩散系数时变模型的解析解形式。姚诗伟［17］应用Laplace 变换方法推导了扩散系数时变条件下Fick第二定律的解析解。杨绿峰等［18］建立了时变扩散系数下的氯离子二维扩散解析解，并考虑混凝土初始暴露龄期的影响而提出了简化计算方法。可见，氯离子扩散系数的时变性不可忽略，正确引入扩散系数时变性才可以准确得到混凝土中氯离子扩散和浓度分布规律。

综上可知，氯离子侵蚀环境下的混凝土结构表面氯离子浓度和扩散系数都具有时变性，需要在混凝土结构耐久性设计中加以考虑。Frederiksen 等［19］研究了表面氯离子浓度呈幂函数变化、扩散系数也为时变函数时，扩散控制方程的双伽玛函数简化形式解析解。事实上，不同环境腐蚀条件下的表面氯离子浓度时变规律存在差异，但上述研究只求解了表面氯离子浓度为幂函数时的解析解，笔者认为有必要结合不同的表面氯离子浓度时变模型，同时考虑扩散系数的时变性，据此研究建立双时变条件下的扩散控制方程解析解，为混凝土结构耐久性分析和设计奠定基础。

本文同时考虑扩散系数及表面氯离子浓度的时变性，利用变量代换法和Laplace 积分变换法求解双时变条件下扩散控制微分方程，求解得到线性模型、平方根模型、幂函数模型和对数模型等4 类不同表面氯离子浓度时变模型的双时变解析解，并据此研究混凝土表面氯离子浓度和氯离子扩散系数时变性对混凝土中氯离子扩散过程的影响。

1 混凝土中氯离子扩散的时变模型

氯盐侵蚀环境下，混凝土中氯离子扩散过程可以采用Fick 第二定律微分控制方程进行描述，即

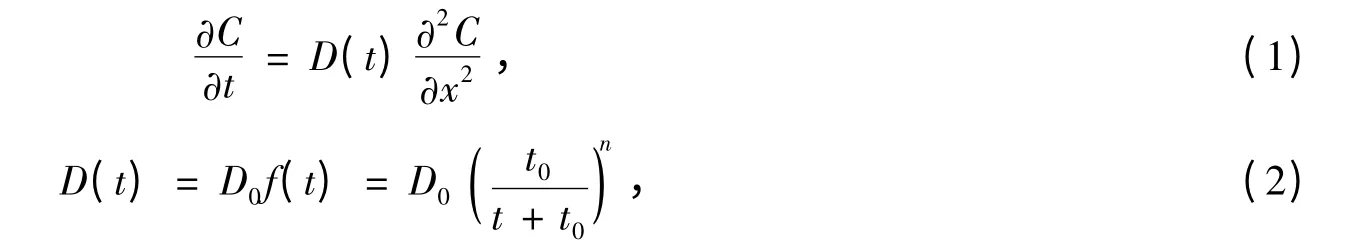
式中，C(x，t)表示暴露时间为t 时，混凝土中距表面x 深度处的氯离子浓度;D(t)为混凝土的氯离子扩散系数，通常采用其表观值;D0为初始暴露龄期t0时刻的混凝土氯离子扩散系数，简称为混凝土的初始龄期扩散系数，可通过RCM 法测得;f(t)为氯离子扩散系数的龄期衰减函数;n 是龄期衰减系数，根据长期暴露混凝土在不同时刻t 的D 值拟合得到。

式(1)应满足初始条件

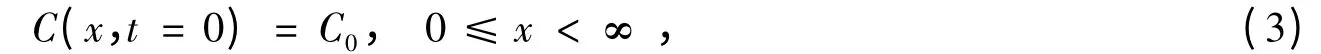
及边界条件

式中，C0为混凝土的初始氯离子浓度;CS(t)为混凝土的表面氯离子浓度时变函数，其时变性通常采用线性［4］、平方根［5］、幂函数［6］和对数［7］等模型描述，应根据实际工程所处环境和混凝土组份选择合适的模型。

2 D 和CS双时变下的解析解

将其在时间域［0，t］上积分，可以求得表达式:

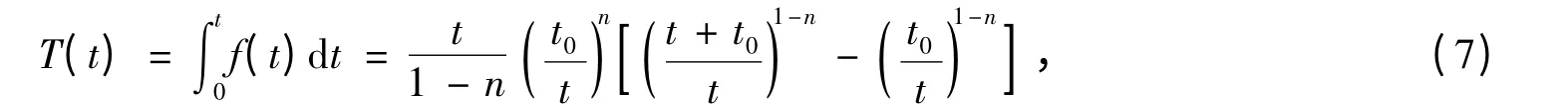
令龄期衰减函数f(t)为变量T(t)的一阶导数，即:

鉴于t0＜＜t，故式(7)可以简化为［18］:

求逆函数得:

考虑式(6)，根据复合函数求导法则，可得:

根据式(7)可知，T 与时间t 的量纲相同，因而，式(1)的初始条件和边界条件可以表达为:

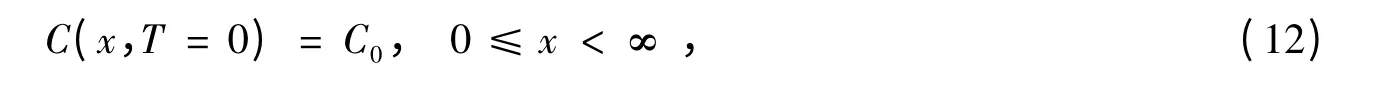
将式(11)、(12)、(13)、(14)联立，引入过余函数G(x，T)=C(x，T)-C0和GS(T)=CS［t(T)］-C0，则上述控制微分方程及其初始条件和边界条件可转化为:

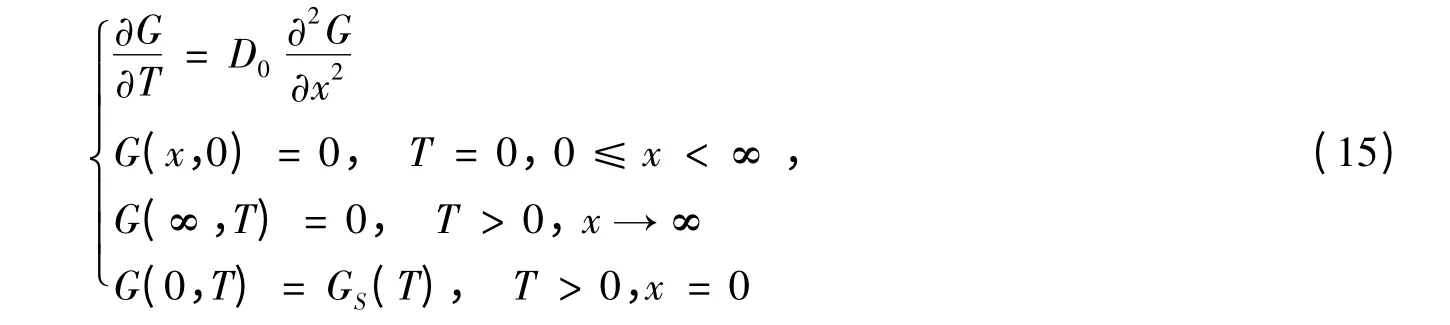
对式(15)各项两边施行对变量T 的Laplace 变换，令:

并代入边界条件得:

求解式(17)的通解为:

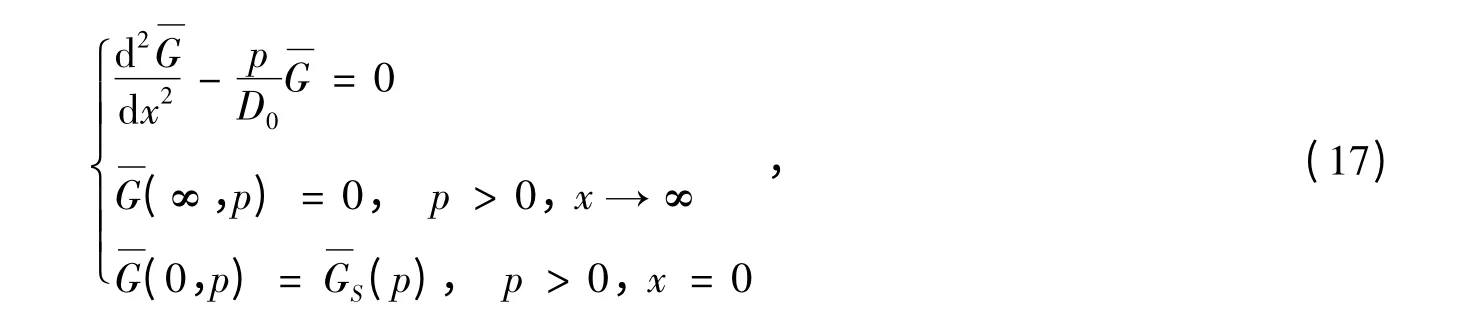
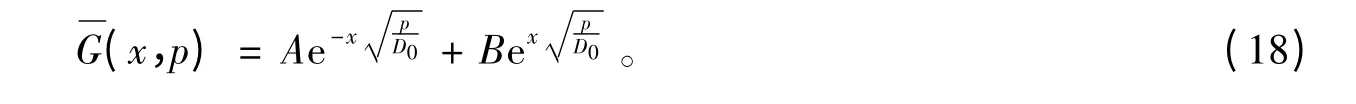
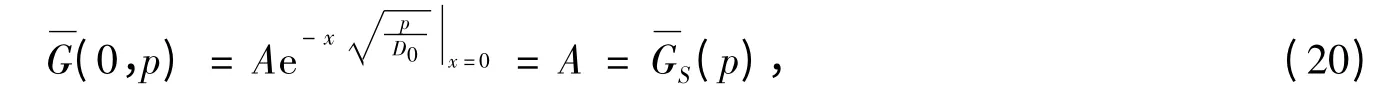
对式(21)两边施加Laplace 逆变换得:

《舌尖1》是找到了菜然后再去发掘背后的故事，《舌尖2》是找了个故事然后让主人公顺便做个菜。看完《舌尖1》，我们体会到，中国人无论生活在什么样的境况中，都在快乐地寻找生命中的美味；但在《舌尖2》，我们认识到，无论做出多么美味的食物，他们的生活始终充满着痛苦离散和磨难。

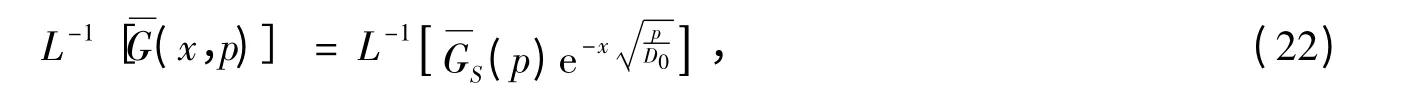
将过余函数G(x，T)=C(x，T)-C0代入，得到任意时变边界条件下扩散系数时变的解析解通式为:

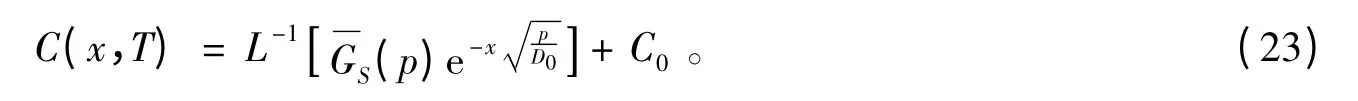
依据Laplace 变换表格，可以将各种不同的CS(t)时变模型代入通式，再将T 用式(8)替换，即可得到与不同表面氯离子浓度时变模型对应的双时变条件下的解析解，该解析解应满足初始条件。

若表面氯离子浓度的时变模型可表示为函数:

式中，C1和α 为时变项系数。当α=1 时，CS(t)为线性模型［4］;当α=1/2 时，CS(t)为平方根模型［5］;当α ＞0 但不等于1 或0.5 时，CS(t)为普通的幂函数模型［6］。此时，可以求得混凝土中氯离子浓度分布的解析解:

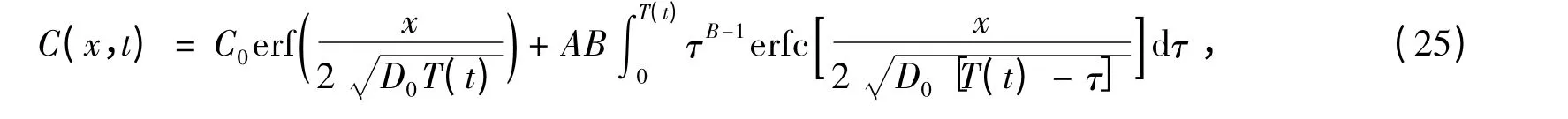
若表面氯离子浓度CS(t)为对数模型［7］:

式中，t ≥1，β 为时变项系数，ε 表示标准时间(通常为1 a 或28 d)的表面氯离子浓度。其解析解可表示为:

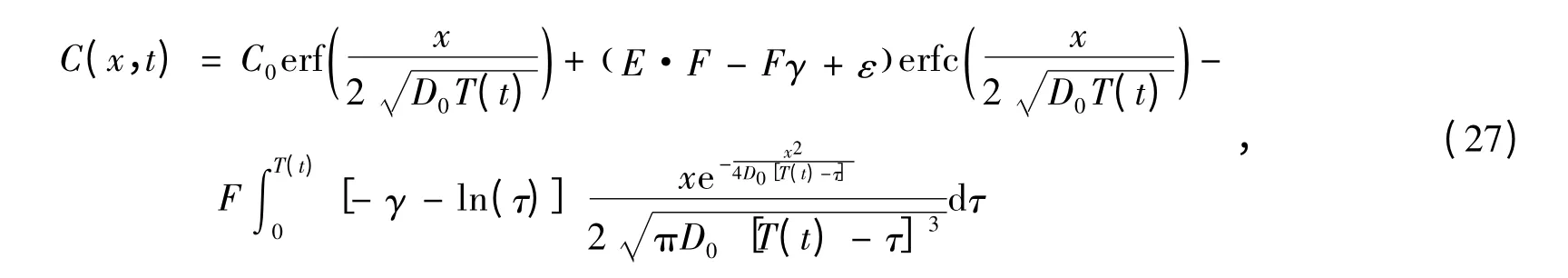
3 算 例

算例:某跨海大桥桥面板混凝土养护28 d 时暴露于海洋氯盐环境，即t0=28 d=0.076 7 a，相应地，氯离子扩散系数D0=5×10-12m2/s=157.68 mm2/a，初始氯离子浓度很小时可以忽略其影响，故取C0=0，保护层厚度70 mm，表面氯离子浓度可选用幂函数模型:

或对数模型:

式中，C1=0.2，α=0.3，ε=0.2，β=0.097。

表面氯离子浓度的两种时变模型如图1 所示。从图1中可以看出，CS随时间增长的速度在前10 a 较快，随后增速逐渐趋于平缓，对数模型表现得更为明显。

利用本文推导的解析解计算以下6 种条件下该混凝土桥面板中氯离子的浓度分布规律。其中，CS为非时变参数时，取CS=0.80%;D 为时变参数时，其龄期衰减系数为0.3，否则取D=D0。

①同时考虑D 和CS的时变性，且CS为幂函数时变模型，其计算结果用D-CP 表示;

②同时考虑D 和CS的时变性，且CS为对数时变模型，其计算结果用D-CL 表示;

③只考虑D 的时变性，其计算结果用DV 表示;

④只考虑CS的时变性，且取幂函数时变模型，其计算结果用CP 表示;

⑤只考虑CS的时变性，且取对数时变模型，其计算结果用CL 表示;

⑥CS和D 都为常数，其计算结果用CT 表示。

为检验本文推导的解析解正确性，将上述6 种情况下桥面板中距暴露面深度为20 mm 处氯离子浓度随时间变化规律的解析解与有限元法计算结果相比较，结果如图2 所示。其中，“1”表示解析解法，“2”表示有限元法。从图2 中可以看出，两种方法的计算结果非常吻合，由此证明了本文解析解的正确性。

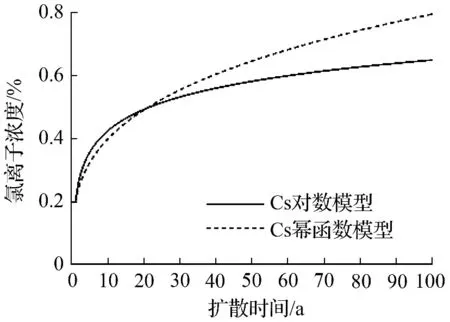
图1 CS积累变化曲线Fig.1 The accumulated curve of CS

进一步地利用本文解析解计算距混凝土暴露面30、50、70 mm 处氯离子浓度随时间变化曲线，结果分别如图3 ～图5 所示。从图中可以看出，图例CT 表示的非时变模型的氯离子浓度最高，图例D-CP 和D-CL 表示的双时变模型的氯离子浓度最低，图例DV、CP 和CL 表示的单时变模型介于非时变和双时变之间。由此说明，CS和D 的时变性对氯离子扩散规律有显著影响，在混凝土结构耐久性设计中应同时考虑CS和D 的时变性。进一步地，对比非时变模型和单时变模型的计算结果，DV 与CT 曲线之间的差距要大于CP、CL 与CT 之间的差距。由此可知，扩散系数D 的时变性对氯离子浓度分布的影响更大。同时可以看出，表面氯离子浓度和氯离子扩散系数的非时变模型、单时变模型和双时变模型等3 类模型对混凝土内的氯离子浓度积聚规律产生了不同影响，这种差异在混凝土较深处更为明显。但是，随着计算深度的增大，特别是D 时变性的影响明显增大。由此说明，混凝土结构保护层越厚，CS和D 的时变性对钢筋表面的氯离子浓度影响越显著，即对钢筋混凝土结构耐久性的影响越大。

对比图1 与图3 ～图5 的氯离子浓度分布规律可以看出，两种不同的表面氯离子浓度时变模型之间的差别随时间增长而逐渐增大，而这两种模型对混凝土内部氯离子浓度分布的影响相对较小，且随着扩散深度的增加而减小。

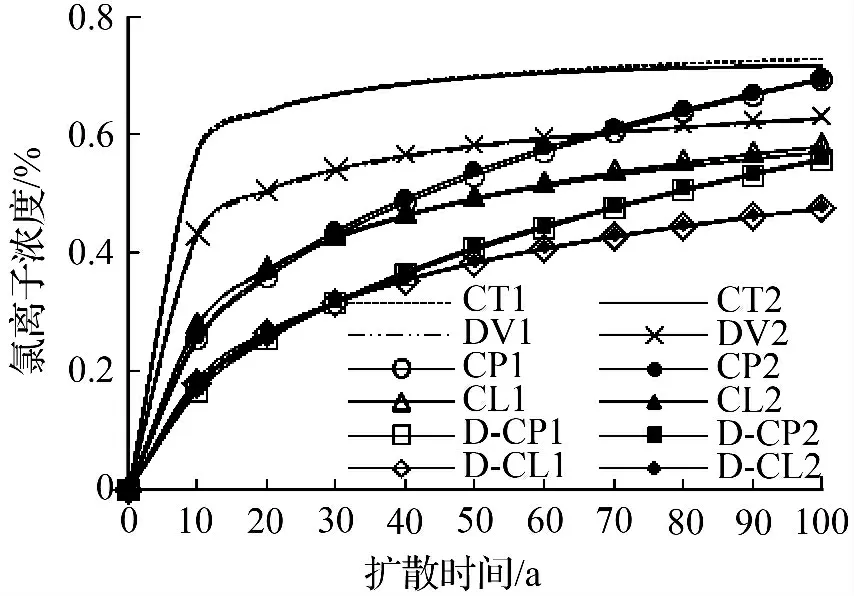
图2 20 mm 处氯离子浓度的解析解和有限元解Fig.2 Chloride concentration at 20 mm by the CFS and the FEM

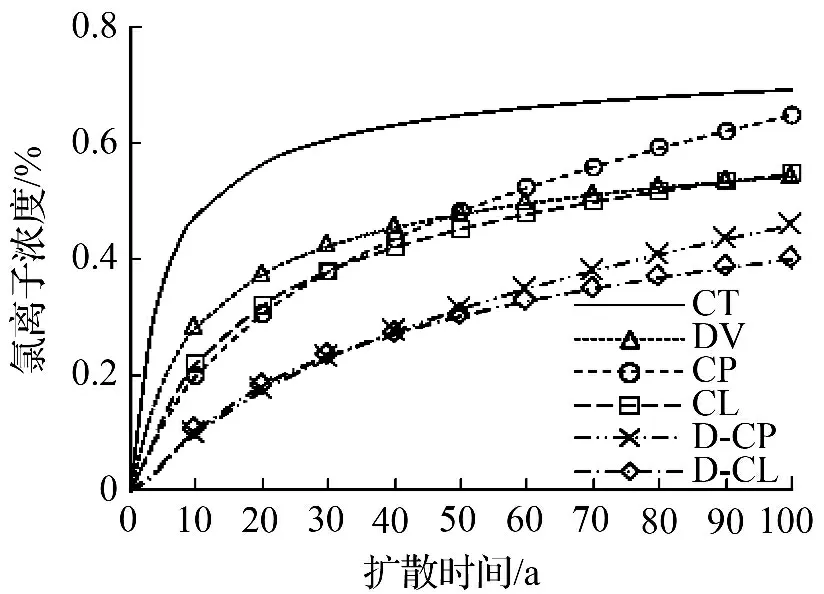
图3 30 mm 处氯离子浓度Fig.3 Chloride concentration at 30 mm

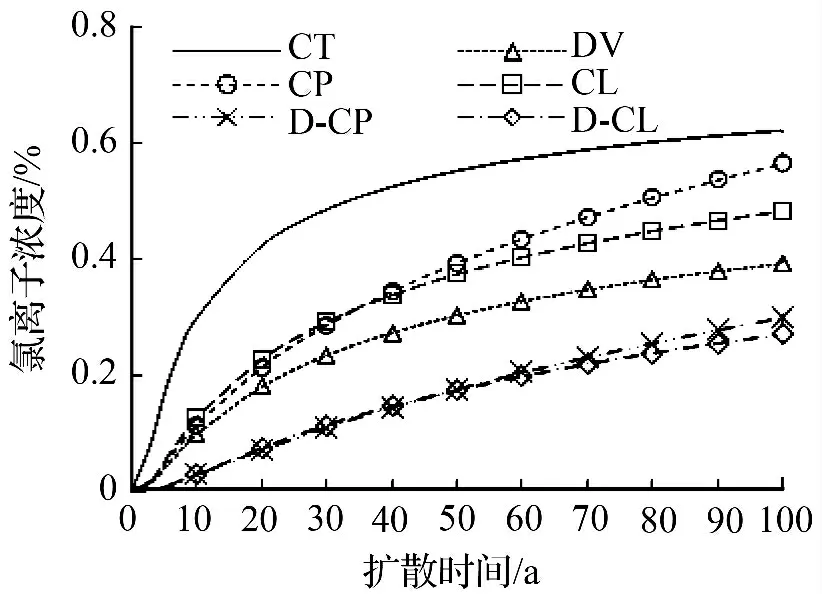
图4 50 mm 氯离子浓度Fig.4 Chloride concentration at 50 mm

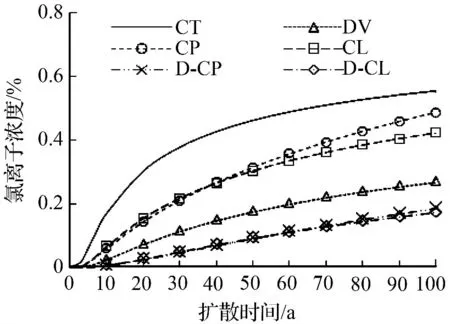
图5 70 mm 处氯离子浓度Fig.5 Chloride concentration of 70 mm

4 结 论

用变量代换法和Laplace 积分变换法求解表面氯离子浓度和氯离子扩散系数双时变条件下氯离子扩散解析解，并通过与有限元法计算结果对比，证明了本文解析解的正确性。研究表明:

①不同CS时变模型之间的差异随时间而增大，且随着扩散深度增大逐渐减小。

②不同CS模型之间的混凝土内氯离子的积聚和浓度分布规律差异较小。CS和D 的时变性都能够对氯离子扩散和浓度分布规律产生显著影响，而且D 时变性相对于CS时变性的影响更大。

③CS和D 的时变性对混凝土内不同深度处的氯离子浓度的影响将随着深度而增大，D 时变性的影响随深度而增大的趋势更明显。

［1］ 施锦杰，孙伟.混凝土中钢筋锈蚀研究现状与热点问题分析［J］.硅酸盐学报，2010，38(9):1753-1764.

［2］ COLLEPARDI M，MARCIALIS A，TURRIZIANI R.Penetration of chloride ions into cement pastes and concretes［J］.Journal of the American Ceramic Society，1972，55(10):534-535.

［3］ 赵羽习，王传坤，金伟良，等.混凝土表面氯离子浓度时变规律试验研究［J］.土木建筑与环境工程，2010，32(3):8-13.

［4］ 王命平，王冰，赵铁军，等.沿海混凝土结构的环境盐雾分区研究［J］.青岛理工大学学报，2007，28(4):1-6，10.

［5］ PETCHERDCHOO A.Time dependent models of apparent diffusion coefficient and surface chloride for chloride transport in fly ash concrete［J］.Construction and Building Materials，2013(38):497-507.

［6］ COSTA A，APPLETON J.Chloride penetration into concrete in marine environment-Part II:Prediction of long term chloride penetration［J］.Materials and Structures，1999，32(5):354-359.

［7］ SONG H W，LEE C H，ANN K Y.Factors influencing chloride transport in concrete structures exposed to marine environments［J］.Cement and Concrete Composites，2008，30(2):113-121.

［8］ KASSIR M K，GHOSN M.Chloride-induced corrosion of reinforced concrete bridge decks［J］.Cement and Concrete Research，2002，32(1):139-143.

［9］ 余红发，孙伟，麻海燕.混凝土氯离子扩散理论模型的研究Ⅱ——基于有限大体的非稳态齐次与非齐次扩散问题［J］.南京航空航天大学学报，2009，41(3):408-413.

［10］ANN K，AHN J，RYOU J.The importance of chloride content at the concrete surface in assessing the time to corrosion of steel in concrete structures［J］.Construction and Building Materials，2009，23(1):239-245.

［11］冯庆革，黄小玲，罗学波，等.含氯盐及不含氯盐混凝土浆体的水化进程研究［J］.广西大学学报:自然科学版，2011，36(4):683-688.

［12］TAKEWAKA K，MASTUMOTO S.Quality and cover thickness of concrete based on the estimation of chloride penetration in marine environments［J］.ACI Special Publication，1988，109(17):381-400.

［13］MANGAT P，MOLLOY B.Prediction of long term chloride concentration in concrete［J］.Materials and Structures，1994，27(6):338-346.

［14］MAAGE M，HELLAND S，POULSEN E，et al.Service life prediction of existing concrete structures exposed to marine environment［J］.ACI Materials Journal，1996，93(6):602-608.

［15］SONG L，SUN W，GAO J.Time dependent chloride diffusion coefficient in concrete［J］.Journal of Wuhan University of Technology-Mater Sci Ed，2013，28(2):314-319.

［16］TANG L，GULIKERS J.On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete［J］.Cement and Concrete Research，2007，37(4):589-95.

［17］姚诗伟.氯离子扩散理论［J］.港工技术与管理，2003(5):1-4.

［18］杨绿峰，李冉.混凝土中氯离子二维扩散规律的解析研究［J］.水利水电科技进展，2009，29(3):20-23.

［19］FREDERIKSEN J M，MEJLBRO L，NILSSON L-O.Fick's 2nd law-Complete solutions for chloride ingress into concretewith focus on time dependent diffusivity and boundary condition［R］.Lund:Division of Building Materials LTH，Lund University，2008:29-32.