浅谈锚杆数值模拟分析以及工程设计应用

梁广昌

（广东省建筑设计研究院 广东广州 510010）

浅谈锚杆数值模拟分析以及工程设计应用

梁广昌

（广东省建筑设计研究院 广东广州 510010）

锚杆广泛应用于岩土工程以及土木工程中，本文主要阐述国内外锚杆数值模拟研究现状以及目前存在的问题，结合实际工程优化锚杆布置，为今后锚杆在工程的应用提供参考。

锚杆；数值模拟；工程应用

1 前言

众所周知，目前锚固技术在实际工程中应用的相当广泛。与实验研究相比较，锚杆的数值模拟特出的优点是减少人力物力的耗费，节约实验资源。在工程中，锚杆主要用于抵抗地下水浮力，现阶段的应用逐渐广泛。

自从1912年德国谢列兹矿最先采用锚杆支护井下巷道以来，锚杆已应用了上百年。由于其成本低、劳动强度轻以及施工方便等优点，成为地下工程建设常用的一种技术。随着新世纪计算机技术的飞速发展，有限差分法、有限单元法[2、3]、边界元法[5]、反分析法、离散元法[6]、界面元法以及块体理论[4]等数值模拟方法逐渐成熟，为学者们研究锚杆提供了理论依据。

2 锚杆数值模拟研究状况

2.1 数值模拟中常用的方法

2.1.1 有限元法

有限元法分析（Finite Element Method，简称FEM）的概念于20世纪40年代问世。1943年，Courant开创了有限元分析法的新纪元。1956年，Turner，Clough，Martin和Topp等人最早定义了三角单元的特性，并首次介绍了经典的确定单元特性的方法——直接刚度法。在1960年，Clough进一步优化了平面弹性问题后，有限元的优势以有效性逐渐被学术界认可。此后，有限元法在工程界获得了一致好评。

2.1.2 边界元法

边界元法（Boundary Element Method，简称为BEM）最早由英国学者Bribbia总结提出。该方法从20世纪60年代开始，在工程设计分析中得到了逐步应用。

边界元法应用格林定理等，通过基本解将微分方程变换算成边界上的积分方程，并在边界上离散数值求解。边界元法有直接法与间接法两种。

2.1.3 离散单元法

离散单元法（Discrete Method，简称DEM）是P.A.Cundall在20世纪70年代提出的数值方法，其主要针对不连续变形块体系统的分析。该方法主要适合于完全节理化的碎裂以及散体结构岩体。

离散单元法以单元刚体运动方程式作为基础，建立代表整个系统状态的显式方程组，结合单元的本构关系，利用动力松弛法进行迭代计算。在迭代计算的过程中各个时步的结果均模拟了块体位移以及转动的全部过程。

2.2 国内外锚固技术数值模拟发展状况

在理论研究方面，传统的解析解存在着数学处理上的困难，局限于受力状态较简单的圆形地下工程，难以模拟围岩和工程的真实性以及复杂性。因此，解析解得到的结论具有有一定程度上的局限性。随着计算机技术的飞速发展，使得人们利用数值方法来研究和解决这一问题成为了可能性[5]。

朱浮声等[8、9]针对锚杆在半无限空间受轴向荷载问题进行了研究分析，提出了利用锚杆拉拔实验来确定锚杆轴力以及粘结力的理论方法。此方法克服了传统的人为定义粘结力分布方法的明显缺点，该方法以粘结力作为单元体附加应力场，得出端部锚固与全长锚固锚杆支护数值模拟的边界元法公式。

Ferrero[11]和Pellett[12]提出了锚杆在轴力和剪力共同作用下，对节理岩体加固作用的数值方法。

Aydan[17]提出了一种修正的锚杆单元，该单元共有四个结点，其中两个结点与钢芯连接，另两个结点与灌浆相连。但该单元并未考虑钢芯与灌浆之间的滑动作用。

Pellet[18]在1996年论文中提出了锚杆在轴力与剪力共同作用下对节理岩体加固作用的数值方法。

Malek Bouteldja[19]在2002年论文中通过有限元数值模拟研究了锚索几何形状、粘结材料、围压等因素对锚固段抗剪刚度有较大影响。

梁广昌[1]在其硕士论文中利用有限元软件ABAQUS对曾镇强[20]论文中实验进行了模拟分析，提出了对锚杆进行动力数值分析产生的误差主要有：滑移机制的差异性、材料本构模型的差异性、锚杆外形的差异性等。文中分析了动力荷载频率对锚杆应变分布的影响，为后续研究工作提供了理论依据以及参数的参考值。

梁广昌[1]论文中研究了锚固长度为280mm（35d）的锚杆在频率为2Hz、4Hz以及8Hz的情况下，锚杆在施加荷载的前、中、后期的应变分布情况如图1～3所示。

图1 锚固长度为280mm前期的应变分布

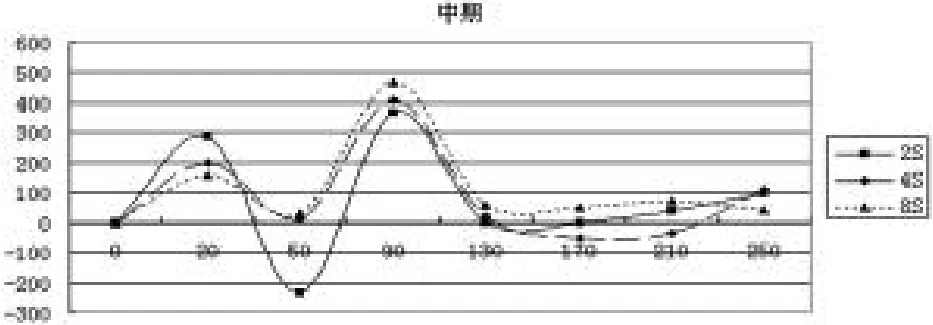
图2 锚固长度为280mm中期的应变分布

图3 锚固长度为280mm后期的应变分布

从图1～3可以看出，当荷载频率逐渐增大时，沿着锚固长度，随着荷载频率的增加，应变有增大的趋势。此现象说明，当施加高频率的荷载时，锚杆应力向锚固深处迅速传递。

3 锚固技术在工程中的应用

（1）清远某项目，场地位于清远市清城区，建筑用地面积5.62 万m2，总建筑面积为38.57万m2，其中地下建筑面积7.8万m2，地上建筑面积30.77万m2。地下室深度为4.925m，土质为中风化砂质页岩，地下水头为4.925m，底板厚度为500mm。该工程采用永久性抗拔锚杆，每根锚杆选用三根直径为25mm HRB400钢筋。锚杆布置如图4所示。

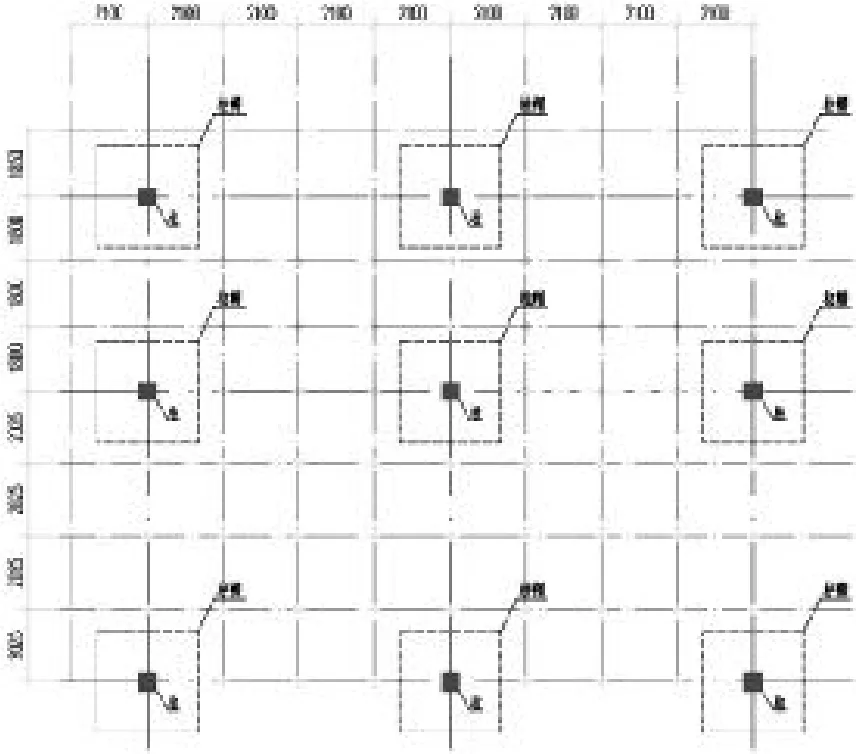
图4 清远项目锚杆平面布置图

如图4所示，锚杆均匀布置于底板下，地下水浮力由锚杆均匀承受，锚杆数量较大。底板承受的水浮力效应较小，经计算，按规范相关要求配构造钢筋，仅双层双向16@200即可，配筋量较小。

该布置方式带来的弊端是增加底板施工的难度。经施工现场反馈，由于锚杆间距较小，难以使用现场施工推车进行材料的输送，极大拖延施工进度。

（2）湛江某体育馆，占地面积4396.62m2，建筑高度为22.3m。地上一层，地下一层，地下室深度为5.6m。土质为中风化石灰岩，地下水头为5m，底板厚度为500mm。该工程采用永久性抗拔锚杆，每根锚杆选用四根直径为25mm HRB400钢筋。锚杆布置如图5所示。

如图5所示，该工程锚杆集中布置于柱帽下，底板不布置锚杆。地下水浮力由锚杆承受。

采用该布置方式使得锚杆数量较清远项目小。由于底板下未布置锚杆，地下水浮力效应较大，除双层双向16@200拉通外，内力较为集中地柱帽处需增加附加钢筋，配筋量较清远项目大。该布置方式明显的优点在于施工方便。由于锚杆间距较大，不会造成施工阻碍，提高施工质量以及效率，缩短施工周期。

图5 湛江某体育馆锚杆平面布置图

（3）广州某地下工程，地下室层数为2层，埋深为12m，水头深度为12m。底板厚度为600mm。该工程采用永久性抗拔锚杆以及抗拔桩共同抵抗水浮力，每根锚杆选用四根直径为25mm HRB400钢筋。

如图6所示，该工程锚杆集中布置在板跨中部，地下水浮力由锚杆与抗拔桩共同承受。

图6 广州某地下工程锚杆平面布置图

目前国内外学者针对锚杆进行了较为深入的研究，但基本上都局限于静力效应。鲜有针对锚杆的动力分析。梁广昌[1]在其硕士论文中研究了数值分析误差产生的原因以及动力荷载频率对锚杆应变分布的影响。

本文通过对比柱帽下布置锚杆以及底板下均匀布置锚杆两种布置方式，得出以下结论：

若采用柱帽下布置锚杆，则减少锚杆数量，增加底板配筋量，降低施工难度，提高施工质量以及速度。

若采用底板下均匀布置锚杆方式，则能较大程度上减少底板配筋量，但随之增加的是锚杆数量以及施工难度，给现场施工带来相当大的不便，并且降低施工质量。

如图4、图5所示，两种布置方式的底板拉通钢筋均为构造钢筋，如采用集中布置在柱帽处的方式，需在柱帽处增加附加钢筋，附加量双层双向为16@200。

综上所述，从受力角度来看，均匀布置方式使得底板受力较为均匀，优于集中布置方式；而从实际应用角度来讲，则集中布置较为合适。集中布置方式可减少锚杆的施工量，提高施工效率，且增加的附加筋仅为柱帽附近，钢筋量较小。综合考虑，集中布置方式优于均匀布置方式。

采用此布置方式的一个显著优点是可有效的降低底板配筋。对于底板而言，锚杆与抗拔桩可视为其支座，因而减少底板的跨度，进而降低底板配筋量，取得了良好的经济效益。且该布置方式结构受力较为合理。从施工角度而言，尽管锚杆间距较小，然而其数量较小且与桩承台距离较大，施工工作面较大，不会增加施工难度。

4 结论

[1]梁广昌.简谐波作用下锚杆数值模拟分析[D].广东工业大学，2013，5.

[2]郝史化，叶玉明，等.ANSYS土木工程应用实例[M].北京：水利水电出版社，2005.

[3]薛守义，刘汉东.岩体工程学科性质透视[M].郑州：黄河水利出版社，2002.

[4]雷晓燕.岩土工程数值计算[M].北京：中国铁道出版社，1999.

[5]张欣.全长粘结式锚杆受力特性以及数值仿真试验研究[D].山东大学，2008，10.

[6]徐恩虎，李贵民，汲长富.巷道锚杆各向异性作用效果的数值分析[J].山东矿业学院学报（自然科学版），1999（3）：10：12

[7]崔俊芝，梁俊.现代有限元软件方法[M].北京：国防工业出版社，1995

[8]朱浮声，李锡润，王泳嘉.锚杆支护的数值模拟方法[J].东北工学院学报，1989，1：1～7.

[9]朱浮声，郑雨天.全长粘结式锚杆的加固作用分析[J].岩石力学与工程学报，1996，15（4）：333，337.

[10]邬爱清，任放，郭玉.节理岩体开挖面上块体随机分布及锚同方式研究[J].长江科学院院报，1991，8（4）：27，34.

[11]Ferrero AM.The shear strength of reinforced rock joints[J].Int J Rock Mech Min Sci Geomech Abst 1995，32：595～605.

[12]Pellet F，Egger P.Analytical model for the mechanical behavior of bolted rock joints subjected to shearing[J].Rock Mech Rock Eng，1996，29：73～97.

[13]漆泰岳.FLAC2D3.3锚杆单元模型的修正及其应用[J].矿山压力与顶板管理，2003，4：50，52.

[14]夏小和，等.穿层锚杆作用效果的DDM数值建模及分析[J].上海交通人学学报，2001，35（4）：499，502.

[15]李宁，赵彦辉，韩炬.单锚的力学模型与数值仿真试验分析[J].西安理工大学学报，1997，13（1）：6，11.

[16]冯光明，等.锚杆初锚力锚吲效应的数值模拟分析[J].煤炭工程，2005，7：46～47.

[17]Aydan O，Koya T、Ichikawa Y et a1.Three-dimensional simulation of an advancing tunnel supported with fore poles，shotcrete，steel fibs and rock bolts[J].Numerical Methods inGeomechanics，Swoboda（ed.），Innshruck，Balkema.1988：1481～1486.

[18]Pellet F，Egger P.Analytical model for the mechanical behaviour of bolted rock joints subjected to shearing[J].Rock Mech Rock Eng,1996，29：73～97.

[19]Bouteldja M.Design of cable bolts using numerical modeling[D].Canada：McGill University，2002.

[20]曾镇强.简谐动力波作用下锚杆的工作机理试验及数值模拟研究[D].广东工业大学，2012，5.

TD353

A

1673-0038（2015）24-0038-03

2015-5-22