天文学家怎样计算节气

□ 萧耐园

天文学家怎样计算节气

□ 萧耐园

本刊2014年11月号刊登题为“节气在公历日期的哪一天”的文章，文中给出两个计算二十四节气中任一节气的公式。此文的目的在于通过这些公式的计算，以具体的例子和数值来直观地说明为什么任何一个节气的公历日期并不固定，经过若干年会漂移1日，经过更多的年份后，甚至飘移2日。不过我们要说明的是，读者诸君在阅读了此文以后，千万别以为天文学家就是用这两个公式来计算节气所在的日期和时刻。那么，事实上天文学家是怎样计算节气的呢？

节气计算关键词一：视位置

中国科学院紫金山天文台编算的《中国天文年历》（以下简称《年历》）关于节气的计算是这么说的：“节气由太阳视位置决定，太阳视黄经为270º时是冬至，以后每隔15º是一个节气。所载节气时刻，系东经120º标准时。”

不同季节太阳的升落

在这段话里我们要注意的关键词是“太阳视位置”和与之相关的“视黄经”。凡是我们在天空上看到的任何天体都能有它的视位置。“视”的意思是地面上的观测者以他的视线把天体直接投影在天球上，在直观上（当然也指通过望远镜）所看到的；“位置”的意思在天文学上特指天体在天球上的投影在某一特定瞬时的天球坐标系里的两个球面坐标，例如在赤道坐标系里的赤经和赤纬，或在黄道坐标系里的黄经和黄纬，等等。太阳视位置是指当地球环绕太阳公转，某一瞬时在轨道上的相应一点，地面上的观测者去观测太阳，视线把太阳投影在天球上计量所得的球面坐标。所谓地球“在轨道上的一点”是指它在宇宙空间与太阳的相对位置。地球在太阳强大引力的作用下，按照开普勒行星运动定律所揭示的规律运动（通常称之为开普勒运动），人们据此能算出它任何瞬时相对于太阳的空间位置，并进而计算太阳（投影）在天球上的球面坐标。从上面引用的话可知就计算节气的时刻来说，太阳的球面坐标只需视黄经。

节气计算关键词二：摄动

但是，上面所说的开普勒运动只是问题的一个方面，另一方面，地球同时还受到月球和各大行星的引力作用。这些引力与太阳引力相比，要微弱得多，在天文学上称为“摄动”。摄动的影响虽小，在精确的测量或计算中却不能忽略。施加摄动的天体（施摄天体）与地球的距离和方向每时每刻都在变化，所以摄动的计算十分烦复。大体上来说，首先要从各个施摄天体的轨道要素出发计算出它们的（球面）位置和到地球的距离，其次根据它们的质量、距离和位置计算它们对地球施加的引力的大小和方向，然后计算这些引力的总和对地球空间位置的影响。把这部分影响加到做开普勒运动的地球位置上去，才能得到地球相对于太阳的真实位置。

《年历》关于太阳位置以及计算摄动用的月球和行星的位置的来源也有说明，即从“2014年起采用DE421”。紫金山天文台历算室在编算每一年的《年历》时，从DE421取得原始数据，用一个相当复杂的程序计算“太阳表”里所列的各个参量，其中就有太阳黄经，每天列出1个数值。我们知道，太阳在天球上沿着黄道做周年视运动，太阳黄经每过1天，几乎增加1°。太阳黄经的数值，不仅每天在变，而且每时每刻在变。所以表列的数值，还必须标明这个数值对应于这天的哪个时刻。表中标明“以力学时0h（时）为准”。力学时是国际天文学联合会决议于1984年采用的一种均匀的时间系统，其中考虑了天体运行中的相对论效应。它与我们日常采用的协调世界时，有确定的换算关系。在2015年，力学时比协调世界时超前68秒。若大致上把这个超前作为为1分，可以认为表列值对应于每天的世界时23时59分，这个时刻对应于上述“东经120°标准时”，也就是北京时间，则是7时59分。

小贴士：DE421简介

DE421是一本星历表的简称。星历表是记载太阳系天体，包括太阳（实质上是地球）、行星和它们的卫星（包括月球）、主要小行星等在天球上的位置以及相关参数（例如它们的轨道要素、质量、半径等）的表册。DE系列星历表是美国喷气推进实验室（Jet Propulsion Laboratory，JPL）利用现代地面测量技术[包括激光测月（LLR）、甚长基线干涉测量（VLBI）和雷达测距（RR）]以及太阳系空间探测获得的资料为基础，根据计及相对论效应的力学模型编制的。这个系列最初的星历表可追溯到上世纪70年代，如编制于1975年11月的DE96，以后不断地利用新的测量资料加以改进，陆续有新版本问世。重要的有DE200，创制于1981年9月，曾经在国际上被广泛长期地使用，后来被1997年5月编制的DE405取代。2007年8月，更精密的DE418编制完成。

DE421是于2008年2月编制完成的，它对DE418做了进一步改进，是当前精度最高的星历表。其中所载月球轨道位置的精度优于1米（相对于地月距离384400千米，相对误差相当于十亿分之一），是根据LLR的资料计算得到的。金星、地球和火星的精度优于1千米（相对误差相当于十亿分之几），其中金星的资料来自对欧洲空间局的金星快车号飞船的RR测量以及对金星快车号和美国的麦哲伦号飞船的VLBI跟踪测量，火星的资料来自对火星探路者号飞船的VLBI跟踪测量。水星的精度为数千米（相对误差相当于亿分之几），是根据对美国的信使号飞船的RR测量资料。木星和土星的精度为数十千米（相对误差相当于千万分之几），资料来自对飞船（木星的伽利略号飞船和土星的卡西尼号飞船）的VLBI跟踪测量。天王星、海王星和冥王星的精度比较差。

24节气立春

24节气立夏

节气计算关键词三：岁差与章动

表列的太阳黄经数值还不能直接用来计算节气，因为表列值是太阳对于年首平春分点的平黄经，而不是对于当天真春分点的视黄经。春分点是黄道坐标系里计量黄经的起点，可是由于地球自转轴的进动，春分点在黄道上几乎以恒定的速率（约50. "3/年，即约25800年沿黄道转过一周）不停地朝着与黄经增加的相反方向，也就是向西退行，这称为黄经岁差。只考虑岁差运动的春分点称为平春分点，而相对于平春分点计量的黄经就是平黄经。可是，春分点除了岁差这种长期运动以外，还有振幅不大的周期性运动，称为章动。章动周期性地改变春分点在黄道上的位置，使之一时向西，一时向东。实际上章动表现为许多不同周期、不同振幅和不同方向的诸项之和。《年历》在计算中取678日月项和687行星项，这些项中周期长于35日的为长周期项，其和用Δψ表示，短于35日的为短周期项，其和用dψ表示。所以说真实的春分点（真春分点）在黄道上的运动是长期性的岁差和周期性的章动的合成。相对于真春分点计量的黄经就是真黄经。

现在我们可以说明上面在提及天球坐标系时为什么必须加上“某一特定瞬时的”这一限定词。由于春分点的岁差和章动，作为天球坐标系计量起点的春分点的位置随时而变，只有确定一个瞬时，才有春分点的确定位置；天体坐标以位置确定的春分点作为计量起点也才有确定的数值。一本记载恒星位置的星表或记载行星和卫星位置的星历表都必须标明表列位置所对应的瞬时，通常称为星（历）表历元。《年历》所载太阳黄经也注明了所对应的历元，即对应于每一年的“年首”。例如2015年的《年历》所载太阳黄经表示为λ2015.0，希腊字母λ在天文学的习惯上用于表示黄经，而下标2015.0则表示2015年年首。年首既然是一个瞬时，我们可能会按照习惯理解为1月1日（元旦）那天的世界时或北京时间0h。其实，天文学上所称的年首这个瞬时与民用的概念不同。首先它以力学时定义，其次天文学上的一年与民用的公历年不同，后者有平年与闰年的差别，年长各不相同，天文学上以365.25日作为1年，称为儒略年，每年的年长相同以方便使用。这样年首便可以是1月1日力学时0h、6h、12h和18h，例如2015年的年首是1月1日力学时6h。

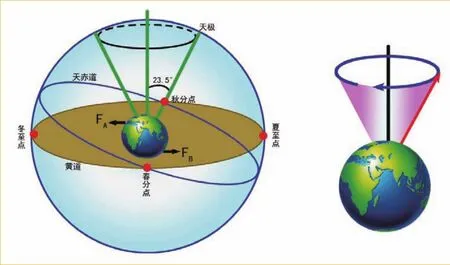
由于太阳和月亮对地球的引力，使得地球在公转时，自转轴就像一个顺时针自转的陀螺摆动，大约2.6万年转动一周。地球在春分点的位置沿着地球公转轨道向西缓慢地移动，大约每2.6万年，春分点的位置在地球公转轨道上移动一周，称为岁差。

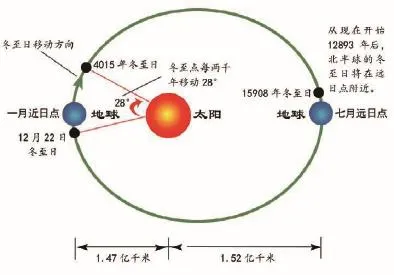
岁差现象的存在，使冬至日在地球公转轨道上并不固定，每年以50角秒260毫角秒顺时针漂移，在25786年的时间里完成一个周期。因此，再过12893年，北半球现在的“冬至点”将在“远日点”附近，而现在的“夏至点”将在“近日点”附近。

24节气立秋

24节气立冬

节气计算关键词四：光行差

真黄经还必须加上光行差改正后才能得到视黄经。光行差是一种附加在被测天体位置上的“视”效应，使得实际测量到的天体位置（视位置）比天体的真实位置（真位置）产生一个或大或小的差值。它起因于光速有限和观测者相对于被测天体的运动。如果真如古人曾经以为的那样光以无限大的速度传播，或者观测者对于被测天体相对静止，那就不会有光行差。可是我们知道光以有限的速度传播，而地球一面环绕太阳运行，一面又绕轴自转，地面上的观测者相对于宇宙空间的天体产生相应的两项运动，这就造成了光行差，依次称为周年光行差和周日光行差。后者的影响比前者小得多，在计算节气时可以忽略。

请看《年历》所载关于太阳黄经的说明：“太阳表中所载黄经系对于年首平春分点的太阳黄经，不含光行差改正，若求对于标准历元J2000.0平春分点的黄经，只要加上量a=－12' 34."34。若求视黄经，可由对年首平春分点的黄经加下列改正：年首到当天的黄经岁差pτ、黄经章动Δψ+dψ，以及光行差改正－20. "49552/R，即

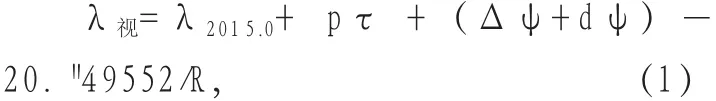
其中p为年首的黄经岁差速率，τ为年首到当天的时间间隔，以儒略年为单位，R为地球向径。对于式（1）这里再略作说明：其中λ视即当天的视黄经；λ2015.0+pτ是把表中所载对于年首平春分点的太阳黄经（λ2015.0）归算为对于当天平春分点的太阳黄经；τ是从1月1日到当天的日数除以儒略年年长，为此先求t=当天的积日－1，所谓积日是从1月1日（作为1）累积计量的日数，从而得τ=t/365.25；加上（Δψ+dψ）是把对于当天平春分点的太阳黄经归算为对于当天真春分点的太阳黄经，《年历》的“太阳表”上也每天列出一个（Δψ+dψ）值；最后一项是周年光行差改正，分母上的“地球向径”是指地球中心到太阳中心的距离，单位为天文单位，“太阳表”上也每天列出一值。

天文学家计算交节日期和时刻的最后环节：逆内插法

紫金山天文台历算室的天文学家们用一个相当繁复的程序在大型计算机上编算《年历》。在编算出“太阳表”中每天的λ2015.0之后，又计算相应日期的λ视。然后通过“逆内插法”的算法来计算每个节气的时刻。在说明什么是逆内插法之前，让我们先了解什么是（正）内插法。《年历》不可能给出每一天任何时刻的某个天文量（例如太阳黄经），只能列出按整点数（例如0h）和等间距（例如1日）计算的一系列这种量。内插法用来解决欲求任何时刻量的问题。在该天文量的表上找到所求日期和下一日期的表列值，用这两个数值的差值按比例算出从整点到所求时刻的差值，加到整点量上就得所求值。举例说明如下：试求2015年6月21日北京时间10时59分的太阳黄经。从当年《年历》的“太阳表”查得6月21日（力学时0h）和6月22日（力学时0h）的太阳黄经为

表列力学时0h相当于北京时间7h59m，要求北京时间10h59m，即力学时3h的值，可通过内插法解决。步骤如下：

求相邻两日的表列值之差（即24h内的变化） 3436".1

从力学时0h到3h相当于1日（24h）的0.125 3436".1×0.125=429".5=7' 9".5

将此值加到6月21日的表列值上 89°20' 10".6+7' 9".5=89°27' 20".1

答案就是89°27' 20."1。这里的运算是所谓的一次内插，使用于表列值变化较慢的场合。如果表列值变化较快，则须应用二次内插或三次内插，步骤复杂得多，不必也不宜在此阐述。明白了内插法，也容易了解逆内插法，无非就是一个逆问题，即已知某年的某个天文量，要求这个量相应的日期和时刻。我们也以一个实例作说明：求201 5年夏至的日期和时刻。我们知道夏至日太阳视黄经为90°。从当年《年历》的“太阳表”可见夏至的时刻在6月21日力学时0h和6月22日力学时0h之间。但是必须首先把表列的平黄经归算为视黄经，查出上列计算λ视的（1）式中的各相应值列于下表。

此外，又查得p的值为5028."796195/儒略世纪。把上列各值代入（1）式，算得λ视后开始逆内插法的运算步骤：

求相邻两日的表列值之差（即24h内的变化） 3436".2

求90º与6月21日的λ视之差 90°－8 9°20' 16".0=39' 43".9=2384".0

求从0h到变化为90°经历的时间 24h×2384."0/3436".2=16h.651=16h39m

这是从力学时0h起算的时间间隔，相应的时刻是6月21日力学时16h39m，化为北京时间要加上7h59m，即得北京时间24h38m。超过了24h，也就是下一日，即6月22日0h38m。查2015年《年历》所列的夏至日期和时刻，我们的结果与之相符。逆内插法是天文学家计算交节日期和时刻的最后一个环节。

自己计算交节日期和时刻的简明方法

读者诸君是否想像天文学家那样自己来计算交节日期和时刻，过一把当天文学家的瘾呢？可是没有大型计算机和程序，甚至连天文年历也没有，怎么来计算。笔者将向你介绍一种简明的近似方法，包括了计算的每个主要环节，让你亲身体会天文学家是怎样计算节气的。

从计算太阳平黄经着手，这由两个环节构成：地球的开普勒运动和摄动。开普勒运动可看作纯粹的椭圆运动，考虑到地球轨道十分接近于圆形，即偏心率很小，把椭圆运动以级数展开，保留偏心率的二次项，得到如下计算太阳平黄经的近似理论公式λ1：

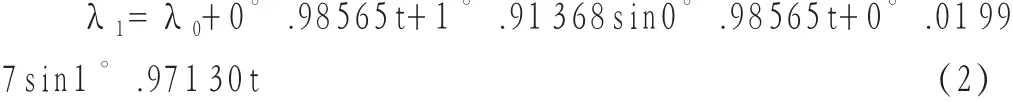
其中右端第一项λ0是太阳的年首平黄经；第二项表示太阳平黄经每天的平均增加量，t的意义同前；后面两项依此表示周年周期项和半年周期项，是对平均量的修正。

作为简明的近似计算不可能从理论上去推算摄动，我们用数值拟合的方法去求得λ0的经验值和摄动效应的经验公式。用1 9年《年历》所载的λ0推算其变化规律，通过计算和比较发现：（1）每4年一个变化周期，平均每4年增加0º.0295；（2）每个周期内，从闰年到下一年平均增加0º.773，从第二年到第三年平均减少0º.249，从第三年到第四年平均减少0º.248。以2000年的λ0=279º.868为标准，按照上述规律可以算得每一年的λ0。例如我们据此计算201 5年的λ0=280º.233=280º13' 59"，与《年历》所载的精确值λ0=280º14' 03"相比仅差4"。

我们用（2）式计算1 9年内每一天的太阳平黄经的近似值，与《年历》所载的同一天的值相减，得到6900余个差值构成的时间序列（1天1值）。用频谱分析和数值拟合方法对此时间序列作分析，得到1个包含1个常数项和3个周期项（两年项、2/3年项和3/8年项）的表达式λ2：

可以认为λ0的变化加上（3）式主要反映了摄动的影响。

把（2）式与（3）式相加，得到计算太阳平黄经λ的半理论半经验的近似公式：

下面让我们用（4）式计算2015年6月21日和6月22日的太阳平黄经λ，取t分别为171和172，得到

再应用（1）式计算视黄经，既然我们这是近似计算，（1）式中的小量（dψ）和R的微小变化可以忽略不计。dψ的绝对值小于0".23，R的相对变化为0.0167，也就是说只能产生约0".34的影响。于是（1）式简化为

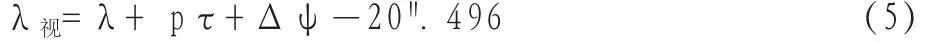
其中Δψ由许多项组成，振幅最大的前两名是周期18.6年、振幅17".2和周期0.5年、振幅1".3的两项，其他项的振幅都小于0".23，我们把它们统统略去，只保留前两项，用一个近似公式表示Δψ：

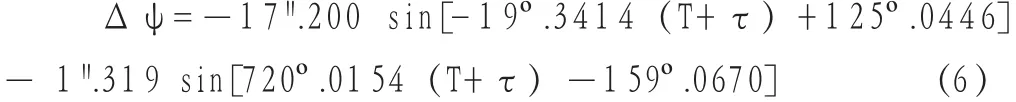
其中T为从2 000年起计的年份数，τ的意义同前 。

做了这样的简化之后，我们就完全不必依赖《年历》了，而计算的主要环节一个不少。计算得到2015年6月21日的Δψ=1".75，与精确值1".80相差无几。最后得到太阳视黄经：

以下逆内插的环节我们已经熟悉，最后算得2015年的夏至交节日期和时刻是6月22日北京时间0h59m，这与准确值相差21分钟，近似计算公式显示了相当大的误差。不过我们的目的在于通过近似计算体验过程并了解过程中的主要环节，而结果的精确度并非追求的目标。

特别说明

让我们回顾本刊去年11月号上的那篇文章，在该文内也计算了2015年的夏至，用的是该文所列的公式，结果与准确值相差较大。计算由2000年的夏至时刻出发，这个数值直接取自《年历》，自然计及当时的摄动。在计算到2015年时，没有计及这时的摄动，却把2000年的摄动带了过来。这摄动的“一进一出”或曰“张冠李戴”，导致一定的误差。引起较大误差的另一个原因是2015年夏至日的黄经章动与2000年的不同，该文的公式不可能计及这一差值。由此可知，该文所列的公式，虽能反映交节日期的变迁规律，但不能精确地给出计算结果，天文学家不会用它们来计算精确的交节时刻。反过来说，本文却难以展现交节日期的变迁规律。因为交节日期变迁的原因是节气循环的周期回归年与历年不一致，这一点在该文所列的公式上彰显无余，却被本文描述的繁复计算掩盖得严严实实。

（责任编辑 张恩红）