磁楔式可调电抗器原理与分析

磁楔式可调电抗器原理与分析

魏新劳，官瑞杨

（哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨 150080）

∶提出一种新的通过调节气隙实现电感量变化的可调电抗器原理。该可调电抗器采用单相双绕组形式，在铁轭中设置了一个受控移动的磁楔，通过调节磁楔插入铁轭的深度来改变磁路中气隙大小，从而实现了电抗器电感值的连续无级可调。结合类比电路进行磁路分析，推导出电感值计算公式；优化一套适用于磁楔式可调电抗器的主要计算公式，并编制设计程序；制作一台实验样机，绘制其电感调节特性曲线。结果表明∶电感值与磁楔插入的深度成一次函数关系式；磁楔完全插入时，电感值最大；磁楔完全抽出时，电感值最小；当磁楔未插入且与铁轭距离很近时，磁楔的位置对电感值也是有影响的。

∶电抗器；磁楔；可调；气隙；电感

0 引言

电力电抗器作为电力系统的重要元件之一，在电力系统稳定、提高电能质量和故障抑制等方面都有着广泛的应用［1-2］。比如，为了提高电力系统中沿线路的电压分布质量，常常需要在合适的位置安装适当功率的并联电抗器以限制沿线电压升高。再比如，为了提高系统功率因数、提高电能传输效率，往往需要在电力系统的适当节点上安装足够容量的有电力电容器和限流电抗器组成的无功功率补偿装置。在所有这些应用中，有些场合并不需要调节电抗器的参数，但有些场合却需要对电抗器的参数进行一定范围内的调整，即∶要求电抗器的参数（主要是电感量或者说无功功率）在一定范围内变化，这种电抗器称为可变电抗器。而且，在一些应用场合还要求电抗器参数必须能够快速变化以适应应用场合的需要，如动态无功功率补偿、动态滤波等场合。

电力系统所使用的可变电抗器包括可调电抗器和可控电抗器两类［3-4］。这两类之间有时也很难界定得非常清楚。一般来讲，通过改变电抗器自身的某些可变因素而使电抗器的参数发生变化的，应该称之为可调电抗器。而将电抗器与一些控制元件结合在一起形成一个综合体，通过对控制元件的操控改变整个综合体的对外表现，实现等效电抗作用改变的，称为可控电抗器。

晶闸管控制电抗器是可控电抗器的典型代表。他是由固定参数的电抗器与晶闸管串联而成，通过控制晶闸管的导通角来控制流过电抗器的电流幅值，从而从整个装置整体看，其等效为一个电感值变化的电抗器。这一方面的另一个典型代表就是基于脉宽调制技术（pulsewidthmodulation，PWM）的可控电抗器［5］，它是由固定参数的电抗器与绝缘栅型双极晶体管（insulated-gatebipolartransistor，IGBT）等电力半导体元件组成的交流开关串联而成，通过调节交流开关导通的占空比调节流过电抗器的电流，从而从整个装置整体看，其等效为一个电感值变化的电抗器。

除了通过调节电抗器线圈匝数调节电抗器电感量外，通过调节电抗器磁路的磁阻调节电抗器的电感量是可调电抗器比较基本的原理。调节电抗器铁心磁路中气隙大小来调节电抗器电感的方法就属于通过调节电抗器磁路磁阻调节电感。在传统的以调气隙大小为调感方式的电抗器结构中，动铁心与定铁心竖直相对，利用传动系统调节动铁心与固定铁心的竖直距离，进而改变电抗器的电感值。这种结构虽然可以实现电感值的连续无级可调，但是在调节过程中，由于动铁心移动方向与磁通流通方向平行，动铁心会受到很大的电磁吸力，再加上其自身重力又很大，使得这种结构的电抗器，不仅电感值调节精度不高，而且电感的调节速度非常慢，甚至会出现电感量与气隙距离关系不能重复的问题。另外，由于动铁心受到很大的交变电磁力作用，使用过程中噪声很大。

本文提出了一种新的磁路气隙调节办法，在这种办法中∶1）动铁心所受电磁力的方向与传统方法中动铁心的受力方向不同；2）动铁心所受电磁力的幅值要比传统方法中动铁心的受力幅值减小很多；3）动铁心的质量比传统方法中动铁心的质量减小很多；4）电抗器的电感量与动铁心的运动距离几乎成线性关系。这些优点使得这种结构的可调电抗器可以比传统结构的可调电抗器具有更好的性能、更广泛的用途。

1 磁楔式可调电抗器工作原理

电抗器其实就是一种电感元件。如图1所示，铁心横截面积为S，磁路总长度为l+l0，其中l0为气隙的长度，l为磁路的软磁材料（硅钢片）部分的长度，在铁心回路上套装一个匝数为N匝的线圈。当在线圈中通人交流电流I时，会在铁心磁路中产生一个磁动势F，在铁心回路中将会产生磁通φ，根据磁路的欧姆定律

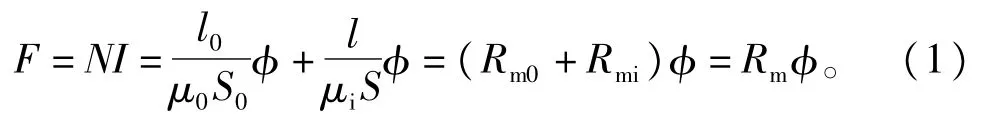
式中∶S0是气隙的等效导磁面积；Rm0为气隙的磁阻；Rmi为铁磁材料的磁阻；Rm为整个磁路的磁阻；μi为铁心磁导率；μ0为空气磁导率。

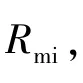
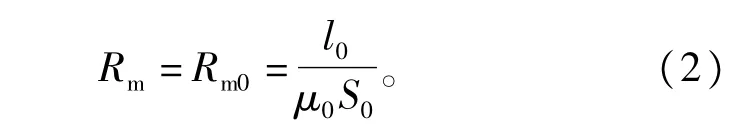
由此可得出铁心电抗器电感值的计算公式为

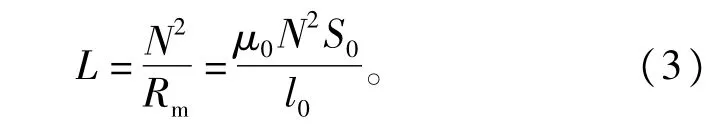
从式（3）可以看出，可以通过调节铁心电抗器磁路中气隙的长度来改变电感值，这就是传统的调气隙式可调电抗器的基本原理［6-9］。

但是从式（3）可以看到，调节气隙的长度实际上是在调节磁路的磁阻。因为，磁路磁阻的调节可以通过其它的方式来实现，所以，也可以通过其它的调节手段调节电抗器的电感值。据此，本文提出在磁路中引人一种称为磁楔的可动部件，通过调节这个（些）磁楔在磁路中的位置来调节电抗器的电感量。

磁楔的材料实际上与磁路中的磁性材料完全相同，而磁楔通过磁通的端面的形状与磁路中磁性材料部分的横截面形状完全相同。事实上，磁楔就可以是从磁路中的磁性材料部分通过线切割技术切割下来的一部分。

磁楔式可调电抗器的基本原理图参见图1。在铁心电抗器的铁扼中设置一个磁楔，该磁楔可以在垂直于铁扼方向自由平滑的插人与抽出，以此来调节磁路中的磁阻大小，实现电感值在大范围内连续可调。

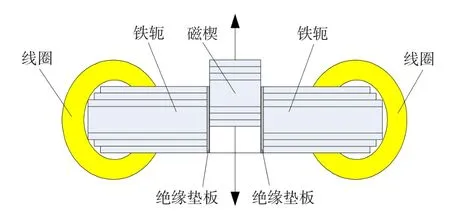
图1 磁楔式可调电抗器基本原理图Fig.1 Magnetic-wedgeadjustablereactor principlediagram

在图1中，当磁楔完全插人到上铁扼中时，铁心结构中气隙最小，此时电抗器具有的电感量最大；当磁楔完全抽出时，铁心结构中出现一个大气隙，此时电抗器具有的电感量最小。当磁楔位于这两个极限位置之间时，电抗器的电感量介于最小电感量和最大电感量之间。

综上可知∶可以通过调节磁楔插人的深度来改变磁路中磁阻的大小，实现电抗器电感值的连续可调。

图1所示电抗器为单相双绕组形式，铁心柱横截面为圆形，铁扼横截面也为圆形。实际设计时，可以让铁扼横截面为矩形，但铁扼横截面面积与铁心柱横截面面积相等。这样便于实现电感量的线性调节。

与传统调气隙式可调电抗器相比，由于磁楔调节的方向与主磁通方向相互垂直，所以在调节过程中磁楔在其运动方向所受到的电磁吸力将会大大减小，这样不仅可以降低振动和噪声，并且可以使磁楔的运动速度得到较大幅度提高，这对于实现电感量的快速调节非常有利。

2 磁楔式可调电抗器调节特性分析

2.1 磁楔完全插入时的电感量

图2（a）所示为当磁楔完全插人到铁扼中的情形，此时，在磁楔两侧有两个大小相同的绝缘垫板。忽略铁心磁阻，磁路中的磁阻主要为磁楔两侧的绝缘垫板的等效磁阻，磁动势全部降落在这两个绝缘垫板的磁阻上。磁路的其类比电路图如图2（b）所示。

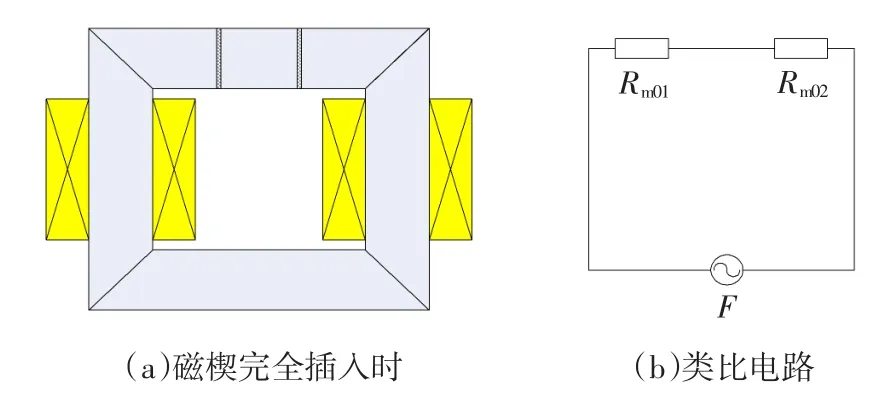
图2 磁楔完全插入时情形及类比电路图Fig.2 Thesituationandanalogycircuitwhen magnetic-wedgeisfullyinserted

由类比电路图可以看出，此时总磁阻为

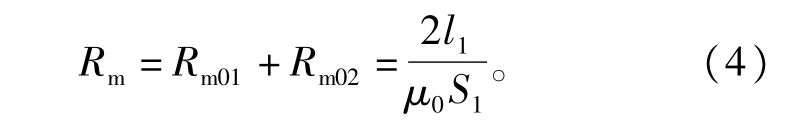
式中∶Rm01、Rm02分别为磁楔两侧的绝缘垫板的磁阻，假设且其大小相等，μ0为空气磁导率；l1为单个绝缘垫板的厚度，S1为单个绝缘垫板的等效导磁面积。此时磁楔式可调电抗器的电感值为最大值，有

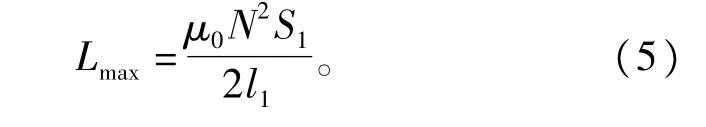
2.2 磁楔完全抽出时的电感量

此种情形如图3（a）所示。当磁楔完全抽出的时候，磁路中的气隙长度最长，假设磁楔的长度为l2，则相当于在磁路中增加了一个长度为l2的大气隙，此时总磁阻为这个大气隙磁阻与两个绝缘垫板的磁阻串联，其类比电路图如图3（b）所示。

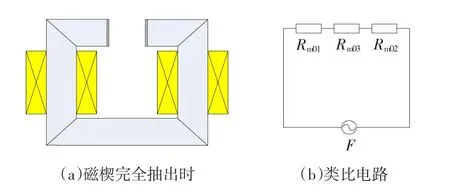
图3 磁楔完全抽出时情形及类比电路图Fig.3 Thesituationandanalogycircuitwhen magnetic-wedgeisfullypulledout

可以得出磁路中的磁阻为

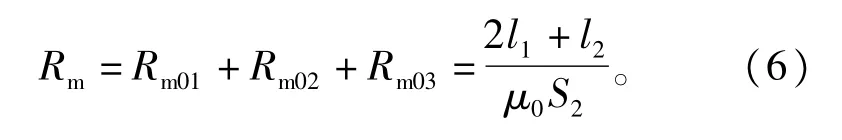
式中∶Rm03为大气隙等效磁阻；l2为磁楔长度（大气隙长度）；S2为磁楔抽出时整个气隙磁阻等效导磁面积，注意这里的S2与上文的S1不同，因为受边缘效应的影响，使气隙等效导磁面积与气隙长度有关。此时磁楔式可调电抗器的电感值为最小电感量，有

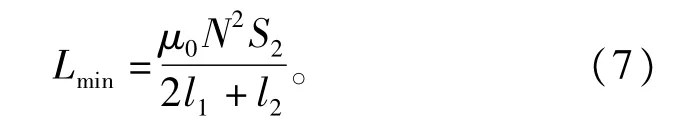
2.3 磁楔部分插入时的电感量

此种情形如图4（a）所示。当磁楔只有一部分插人到铁扼中时，可以认为整个磁路中有3个气隙磁阻，分别为∶磁楔两侧部分绝缘板的磁阻和与磁楔并联的气隙磁阻（包含一部分绝缘板）。其类比电路图如图4（b）所示。

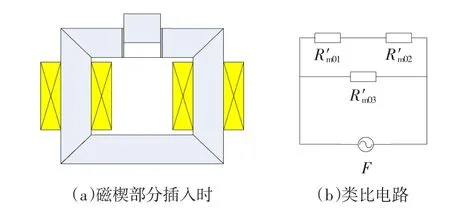
图4 磁楔一部分插入时类比电路图Fig.4 Thesituationandanalogycircuitwhen apartmagnetic-wedgeisinserted

此时电抗器的电感值在最大值与最小值之间，具体电感量可以根据磁楔插人的深度求出。总磁阻为

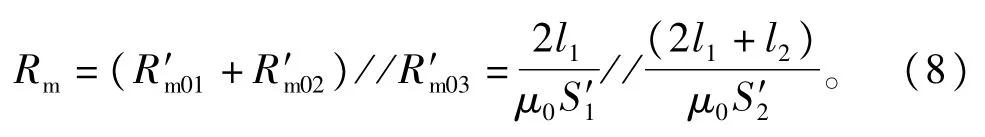
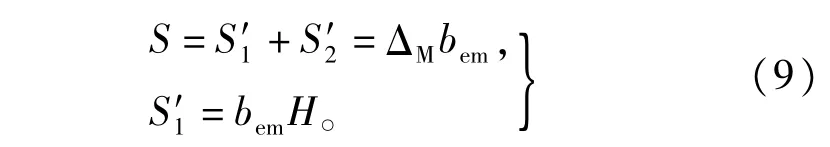
式中∶S为上铁扼截面面积；ΔM为上铁扼总厚度；bem为上铁扼片高度；H为磁楔插人到上铁扼中的深度。由此可以求出此时磁楔式可调电抗器的电感值为

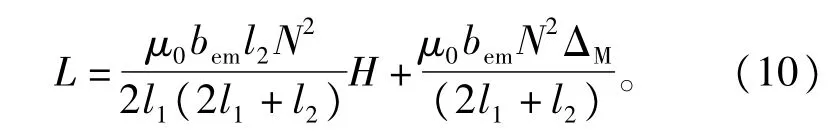
从式（10）可以看出，对于一个具体的磁楔式可调电抗器样机而言，其电感值L与磁楔插人的深度H成一次函数关系式，该线性关系说明了磁楔式可调电抗器的电感量具有线性调节特性。

3 磁楔式可调电抗器的设计计算

本文所介绍的磁楔式可调铁心电抗器，在设计计算方面与普通铁心电抗器的设计计算基本相同。区别在于磁楔式可调铁心电抗器需要分别针对最大容量和最小容量进行两次计算，而普通铁心电抗器则只需要针对一个容量进行一次计算即可。

本文专门设计、编制了磁楔式可调铁心电抗器设计计算软件［10］，只要输人必要的电抗器性能指标参数，软件就可以完成整个电抗器的设计计算工作。图5所示为该设计软件的整体流程图。

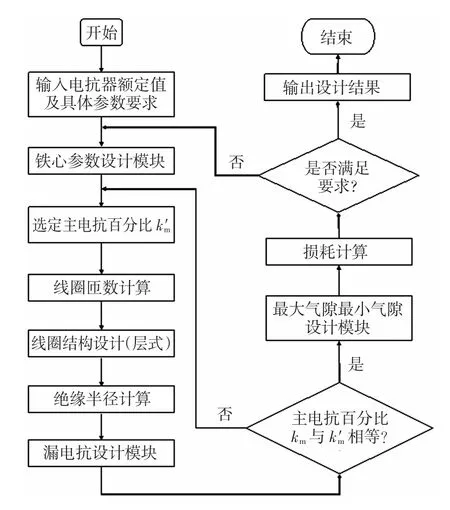
图5 设计计算整体流程图Fig.5 Theflowchartofmainprogram

下面根据具体设计模块依次给出磁楔式可调电抗器的主要设计计算公式［11-14］。

3.1 铁心参数设计模块

1）铁心直径初算

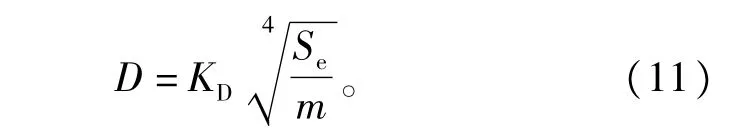
式中∶KD为铁心直径经验系数，对于冷轧硅钢片、铜导线，KD=0.054～0.058，铝导线的KD=0.05～0.054；Se为最大工作容量，单位以kVA计算；m为装有线圈的铁心柱数，一般单相m=2，三相m=3；铁心直径可以取D的计算值附近的标准值。

然后根据铁心直径可以查阅有关铁心直径参数表确定∶铁心柱有效面积Az，铁心最大片宽BM，铁心总厚度ΔM，铁心级数，铁心叠片系数kdp。

2）铁扼片高计算

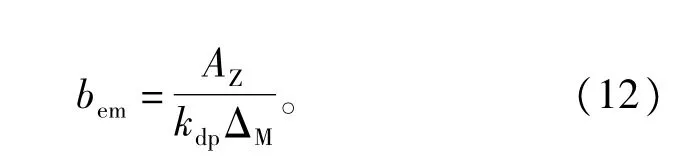
3.2 线圈匝数计算

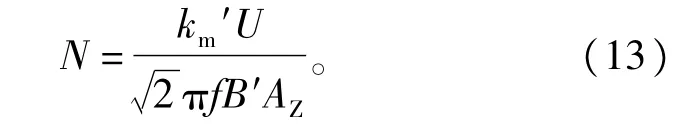
式中∶k'm为考虑到漏抗压降的影响系数，一般k'm= 0.85～0.95，注意这里必须选取k'm，因为该式是在忽略掉漏电抗的情况下推导出来的；U为电抗器的额定工作电压；f为工作频率；B"为初选最大磁通密度。

3.3 线圈结构设计与绝缘半径设计

磁楔式可调电抗器的线圈结构设计和绝缘半径设计原则可参照变压器线圈设计计算准则［15］，这里不再赘述。

3.4 漏电抗设计模块

1）洛氏系数计算

线圈的漏磁通都是与线圈外径侧的空间形成闭合磁路，在线圈以外的空间，漏磁通发散，漏磁通磁路的面积增大。为计及线圈以外空间那部分磁路的磁通，本文参照变压器漏抗计算办法，将线圈高度除以一个小于1的系数作为漏磁通磁路的等效长度［16］，该系数称为洛氏系数。其公式为

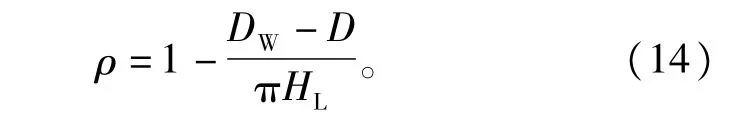
式中∶DW为线圈外直径；HL为线圈高度。

2）漏磁通等效面积计算

传统计算线圈漏磁通等效面积计算公式为

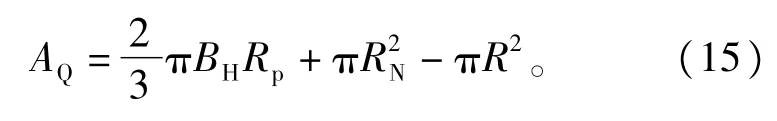
式中∶RP为线圈平均半径；R为铁心半径；BH为线圈厚度；RN为线圈内半径。

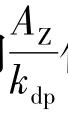
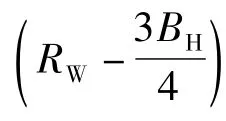
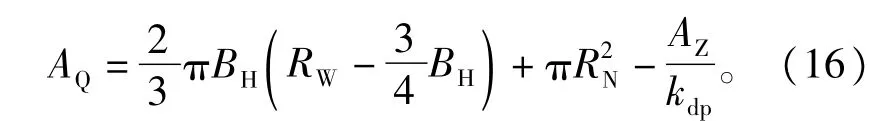
3）漏电抗计算公式

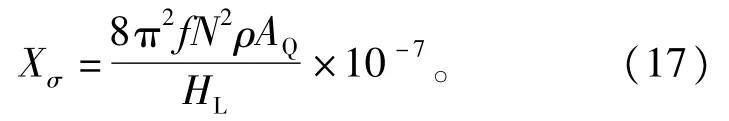
3.5 气隙设计模块

气隙的大小直接影响电抗器电感值，因此，该部分是磁楔式可调电抗器设计计算中的重点内容。当磁通流经气隙时，会在气隙处发生边缘效应，使气隙等效导磁面积扩大。然而，目前有关文献［17-18］记载的气隙等效导磁面积计算都仅仅是理论上的推导，得不到实际证实，且其涉及的气隙范围比较小。当气隙很大时，没有直接可供参考依据。因此精确计算出电抗器中气隙的实际大小是此类电抗器设计计算的难点。

1）气隙等效导磁面积扩大系数计算

通过ANSYS的大量仿真计算，构建电抗器的三维电磁场仿真模型，应用LMATRIX宏命令计算线圈电感值［19-20］，并结合电抗器计算公式反推计算出气隙等效导磁面积扩大系数。对得出的数据进行曲线拟合，找到了不同铁心直径时气隙等效导磁面积扩大系数的一些规律。以铁心直径为80mm为例，气隙等效导磁面积扩大系数［21］计算公式为

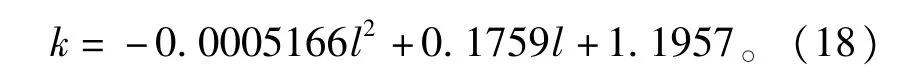
式中∶l为气隙的长度（l＜170mm），单位以mm计算。

2）最大气隙时主电抗计算

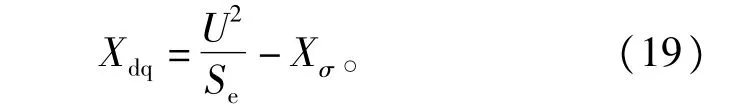
3）最小气隙时主电抗计算

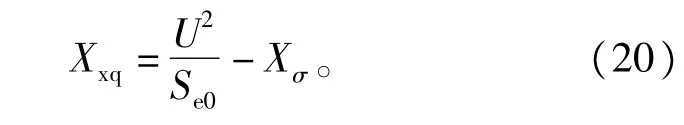
式中Se0为最小工作容量。

4）最大气隙长度计算

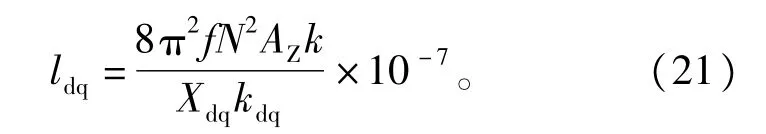
5）最小气隙长度计算

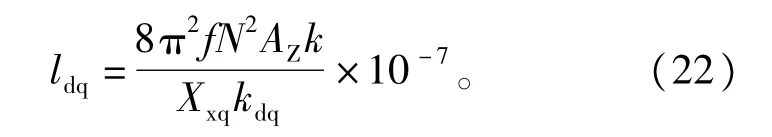
3.6 损耗计算模块

磁楔式可调电抗器的损耗设计计算内容与变压器损耗计算相类似，这里不再赘述。

4 实验样机研制及实验

4.1 实验样机研制

为了验证新型可调电抗器的可行性，同时也是为了验证以上相关分析的正确性，本文设计并制作了一台磁楔式可调电抗器样机，如图6所示，并对其进行验证性实验。表1给出了该电抗器样机具体设计参数。

图6 磁楔式可调电抗器样机Fig.6 Theexperimentalprototypeof magnetic-wedgeadjustablereactor

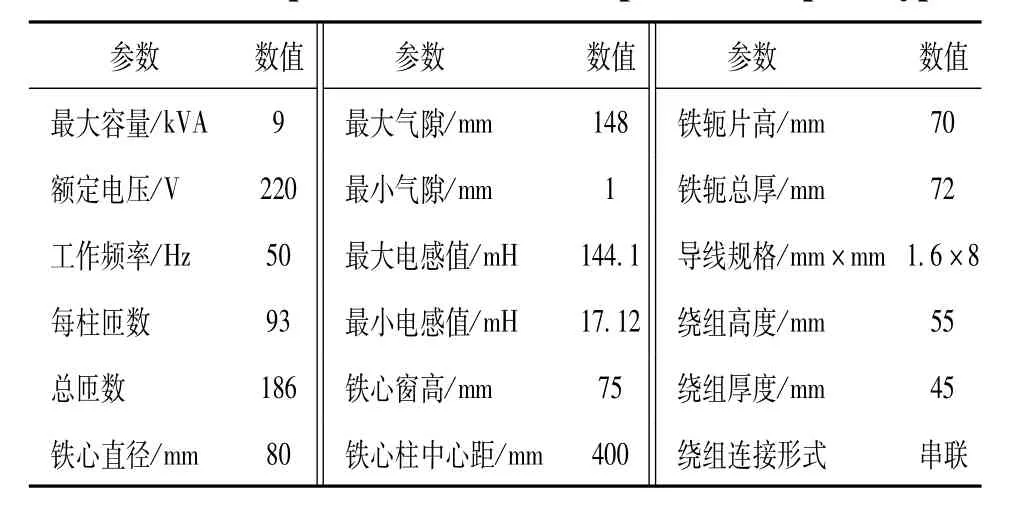
表1 磁楔式可调电抗器样机参数表Table1 Theparametersoftheexperimentalprototype

为了方便调节磁楔插人的深度，控制部分采用了宁波仪表电机厂生产的YYCJZ60-6型直线往复电动机作为磁楔调节驱动电机，并设计了相应的驱动控制器。

4.2 实验结果及分析

实验主要是测试样机的电感调节特性。也就是图7中的插人深度与样机的电感量之间的关系。

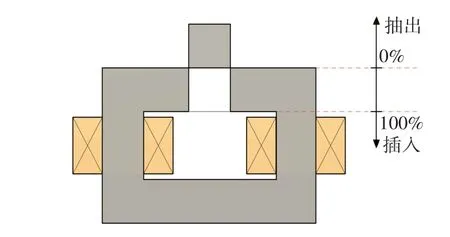
图7 插入深度的定义Fig.7 Thedefinitionofdepthmagnetic-wedgeinserted

电感测量设备为日本HIOKI公司生产的3532-50LCR测试仪，它是一个频率在42Hz～5MHz之间、可同时测量L、C、R的高精度测试设备。实验时，频率选为50Hz，根据实际测量数据绘制的电感调节特性曲线如图8所示。

从图8可以看出∶

1）当磁楔位于铁扼外时（对应插人深度为负值），磁楔的位置对电感量也是有影响的。只是这时的调节曲线比较平坦，说明电感量对距离的变化不敏感，当其距离大于20mm（对应图中横坐标-27.78％）时，电感值不再受磁楔位置的影响，此时测量的电感量就应该是电抗器的最小电感值，实测结果为19.7mH，设计的最小电感值为17.12mH，偏差达15.1％。可能的主要原因是∶磁楔完全抽出之后，气隙长度很大（达148mm），气隙等效面积扩大系数的取值没有直接可供参考的数据，存在取值偏差。

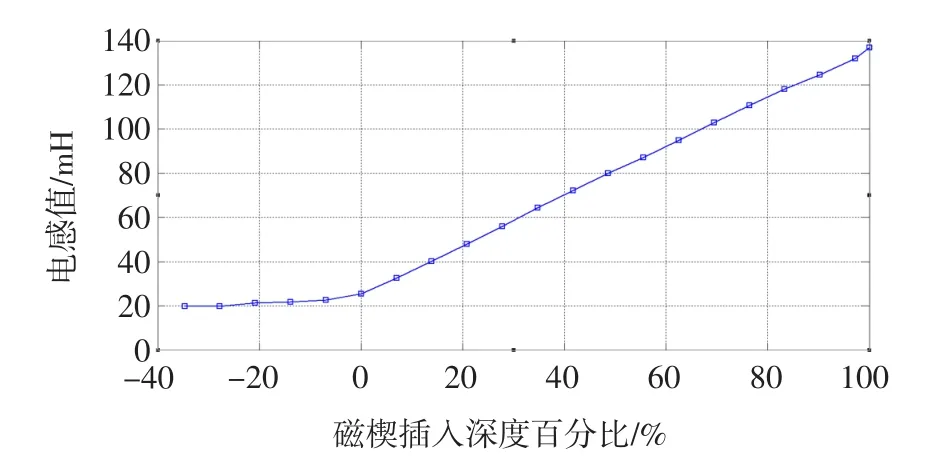
图8 电感调节特性曲线图Fig.8 Theadjustableinductancecurve

2）在插人深度0～100％这一段，电感量与插人深度的关系是线性关系，这表明这种电抗器在其主要调节范围内确实具有线性调节特性，这使得这种电抗器有可能实现快速调感。

3）当插人深度为100％时，电抗器的电感量为最大，实测电感值最大值为136.81mH，设计计算的最大电感值为144.1mH，偏差为5.1％。可能的主要原因是没有考虑铁心回路磁性材料的磁阻，因为此时气隙很小，铁心回路磁性材料的磁阻与气隙磁阻相比并不是无限小量，此时忽略铁心回路磁性材料的磁阻就会导致偏差。

5 结论

本文提出了一种新的可调电抗器调节结构，对这种电抗器的电感调节特性进行了理论分析，分析结果表明∶这种电抗器的电感量具有线性调节特性；给出了这种电抗器的设计流程和主要的设计计算公式；设计制作了样机并对样机进行了实验研究，结果不仅验证了这种电抗器调感原理的正确性，同时也证实了这种电抗器确实具有线性的电感调节特性。

∶

［1］牟宪民，王建啧纪延超.可控电抗器现状及其发展［J］.电气应用，2006，25（4）∶1-4. MOUXianmin，WANGJianze，JIYanchao.Cotrollablereactor presentsituationanddeveopment［J］.ElectricalApplications，2006，25（4）∶1-4.

［2］孔宁，尹忠东，王文山，等.电抗器的可控调节［J］.电气应用，2011，30（5）∶40-44. KONGNing，YINZhongdong，WANGWenshan，etal.Reactor controladjustment［J］.ElectricalApplications，2011，30（5）∶40 -44.

［3］LIUWenye，LUOLongfu，DONGShuda.Thesummarizeofpower controllablereactortechnology［C］//2010the3rdInternational ConferenceonPowerElectronicsandIntelligentTransportation System，2010∶29-33.

［4］冼冀，程汉湘.三相磁阀式可控电抗器综述［J］.电气技术，2014，（1）∶1-3. XIANJi，CHENGHanxiang.Three-phasemagneticvalvecontrollablereactorsummary［J］.ElectricalTechnology，2014，（1）∶1 -3.

［5］程汉湘，何绍洋，黄超宪.磁控电抗器的电磁特性分析［J］.变压器，2013，50（8）∶1-4. CHENGHanxiang，HEShaoyang，HUANGChaoxian.Electromagneticpropertiesofmagntronreactoranalysis［J］.Transformer，2013，50（8）∶1-4.

［6］黑建明.高压可调电抗器设计原理［J］.变压器，1994，25（4）∶5-8. HEJianming.Highvoltageadjustablereactordesignprinciples ［J］.Transformer，1994，25（4）∶5-8.

［7］张愈鲁.铁心电抗器的设计［J］.高压电器，2001，12（2）∶16 -19. ZHANGYulu.Reactorcoredesign［J］.High-voltageElectrical，2001，12（2）∶16-19.

［8］朱旭东.高压可调电抗器原理和计算［J］.高压电器，2012，6∶4 -8. ZHUXudong.Highvoltageadjustablereactortheoryandcalculation［J］.High-voltageElectrcal，2012，6∶4-8.

［9］朱宝森，关毅，陈庆国，等.正交磁化可控电抗器的设计与特性分析［J］.电机与控制学报，2012，16（5）∶26-32. ZHUBaosen，GUANYi，CHENQingguo，etal.Orthogonalmagnetizationcontrollablereactordesignandcharacterization［J］.E-lectricMachinesandControl，2012，16（5）∶26-32.

［10］朱敏，魏新劳，王永红，等.空心电抗器计算机辅助设计系统的开发［J］.黑龙江电力，2003，25（5）∶344-347. ZHUMin，WEIXinlao，WANGYonghong，etal.Development ofcomputer-aideddesignhollowreactorsystems［J］.Heilongjiangpowersystem，2003，25（5）∶344-347.

［11］蒋守诚.铁心电抗器的原理及计算（上）［J］.变压器，1994，13（5）∶5-12. JIANGShoucheng.Reactorcoreprinciplesandcalculation（previous）［J］.Transformer，1994，13（5）∶5-12.

［12］蒋守诚.铁心电抗器的原理及计算（下）［J］.变压器，1994，14（1）∶1-11. JIANGShoucheng.Reactorcoreprinciplesandcalculation（next）［J］.Transformer，1994，14（1）∶1-11.

［13］孙彭年，辛小南，王利川.带气隙铁心电抗器铁心尺寸计算的代数求根法［J］.变压器，1995，4∶5-9. SUNPengnian，XINXiaonan，WANGLichuan.Gappedcorereactorcoresizecalculationmethodofalgebraicroots［J］.Transformer，1995，4∶5-9.

［14］赵亮，张建军.干式带气隙铁心电抗器电感计算方法［J］.高压电器，2012，48（6）∶61-64. ZHAOLiang，ZHANGJianjun.Thecalculationofdry-corereactorinduction［J］.High-voltageElectrical，2012，48（6）∶61 -64.

［15］朱英浩.油浸电力变压器设计手册［M］.沈阳∶沈阳变压器有限责任公司，1999∶20-52.

［16］王云龙.磁阀式可控电抗器设计计算［D］.哈尔滨∶哈尔滨理工大学，2011.

［17］潘三博，陈乔夫.大气隙铁心电抗器气隙等效导磁面积计算［J］.变压器，1998，35（3）∶11-14. PANSanbo，CHENQiaofu.Reactorcoreairgapmagneticgapequivalentareacaculation［J］.Transformer，1998，35（3）∶11 -14.

［18］陈乔夫.铁心电抗器气隙等效导磁面积的计算［J］.变压器，1988∶7-9. CHENQiaofu.Reactorcorecomputingequivalentmagneticair gaparea［J］.Transformer，1988∶7-9.

［19］张倩，胡仁喜，康仕廷，等.电磁学有限元分析从人门到精通［M］.北京∶机械工业出版社，2010∶236-255.

［20］谢龙汉，耿煜，邱婉，等.ANSYS电磁场分析［M］.北京∶电子工业出版社，2012∶111-289.

［21］官瑞杨，魏新劳，聂洪岩.铁心电抗器气隙等效导磁面积计算［J］.哈尔滨理工大学学报，2014，19（4）∶6-11. GUANRuiyang，WEIXinlao，NIEHongyan.Thecalculationof theairgapequivalentcrosssectionalareaincorereactor［J］. HarbinUniversityofScienceandTecnologyJournal，2014，19（4）∶6-11.

（编辑∶刘琳琳）

Theoryandanalysisofmagnetic-wedgeadjustablereactor

WEIXin-lao，GUANRui-yang
（CollegeofElectricalandElectronicEngineering，HarbinUniversityofScienceandTechnology，Harbin150080，China）

∶Anewkindofadjustablereactorprinciplewaspresentedwhichachievestheinductancevalue changedbyadjustingtheairgap.Intheadjustablereactor，aformofsingle-phaseanddouble-winding wereadopted，acontrolledmoveablemagnetic-wedgewassetintheupperyoke，byadjustingthedepthof magnetic-wedgeinsertedinupperyoketheairgapsizewaschangedinthemagneticcircuit，andthecontinuoussteplessadjustmentoftheinductancevaluewasachieved.Combinedwiththeanalogyelectriccircuitsitsmagneticcircuitwasanalyzed，anditsinductanceformulawasdeduced；themaindesignformula wasoptimizedforapplyingonthismagnetic-wedgeadjustablereactor，andadesignprogramwasmade；anexperimentalprototypewasproduced，anditsadjustableinductancecurvewasplotted.Theresult showsthattherelationshipbetweeninductancevalueandthedepthofmagnetic-wedgeinsertedisalinear function；theinductancevalueismaximum，whenmagnetic-wedgeisfullyinserted；whiletheinductance valuebecomestheminimumone，whenmagnetic-wedgeisfullypulledout；whenmagnetic-wedgeisclose totheupperyokebutnotinserted，thepositionofmagnetic-wedgecanalsoaffectinductancevalue.

∶reactor；magnetic-wedge；adjustable；airgap；inductance

∶TM47

∶A

∶1007-449X（2015）11-0032-07

∶2014-09-16

∶国家自然科学基金（51277046）；高等学校博士学科点专项科研基金（20122303110007）

∶魏新劳（1960—），男，博士，教授，博士生导师，研究方向为高压电器设备设计和绝缘检测；官瑞杨（1988—），男，硕士，研究方向为可调电抗器研制及高电压试验技术。

∶官瑞杨

DOI∶10.15938/j.emc.2015.11.005