定子槽开口对感应电机转子涡流损耗的影响

鲍晓华，梁娜，方勇，王汉丰（合肥工业大学电气与自动化工程学院，安徽合肥 230009）

定子槽开口对感应电机转子涡流损耗的影响

鲍晓华，梁娜，方勇，王汉丰
（合肥工业大学电气与自动化工程学院，安徽合肥 230009）

∶为了精确计算感应电机转子上的涡流损耗并探讨定子开槽对其产生的影响，对于额定功率为2.2kW极对数为4的小型铸铭转子感应电机中转子涡流损耗情况进行了详细分析。通过建立不同定子槽开口的电机模型，结合电机内谐波磁场的理论分析与二维有限元的计算方法，研究了电机气隙谐波磁场与定子槽开口的关系，揭示了转子中不同位置的磁密与涡电流分布情况，并对比分析了不同槽开口模型中转子铁心与导条中涡流损耗的大小关系。仿真结果表明∶气隙中的谐波磁场以及转子铁心表面的涡电流密度都随着定子槽开口增大而增大；转子铁心及导条中的涡流损耗随定子槽开口的增大呈二次函数的增长趋势。

∶感应电机；槽开口；谐波磁场；涡流损耗；二维有限元

0 引言

随着社会的日益发展，节能已成为社会各个领域的重大课题。电机作为现代生活的必需品，其能耗受到了社会的广泛关注。感应电机的附加损耗通常按照国家标准规定占电机输人或输出功率的0.5％计算。而对于压力铸铝的小型感应电机而言，这个数值可能会达到2％～3％，甚至以上［1］。电机中附加损耗太大会导致电机的温升严重、绝缘破坏，也会使得电机总的损耗增加、效率降低，对电机的一些经济性能产生影响［2-4］。电机负载时附加损耗包括定子绕组和绕组端部附近金属部件中的涡流损耗以及转子中的涡流损耗等。而本文则将转子中的涡流损耗作为研究对象，并探究其与定子槽开口之间的关系。

国内外有许多关于转子涡流损耗的研究∶周凤争［5］和DaisukeHiramatsu等人［6］采用考虑转子集肤深度和涡流磁场影响的解析模型分别计算了高速电机和同步电机的转子表面损耗；常正峰等人［7］运用传统的二维解析法对实心转子表面的涡流损耗进行了计算，同时也分析了定子槽口宽和气隙长度变化对转子涡流损耗的影响；YanhuiGao［8］，O.J.Antunes［9］，Y.Takahashi［10］等人在二维有限元分析中选择了非协调网格技术和简化时间周期的误差校正方法精简的计算了铁心和第二导体的杂散损耗；HungVuXuan［11］和JianLi［12］等人使用非线性有限元法对不同类型永磁电机的转子涡流损耗进行了分析；梁艳萍等人［13］建立了三维涡流场模型，采用三维有限元分析了双屏蔽复合转子电动机的涡流损耗情况。

对于转子涡流损耗影响因素的分析很少文献从其对电机内电磁场的影响方面人手考虑；在涡流损耗的计算上也很少文献有涉及到转子导条上涡流损耗的计算。本文则主要从分析定子槽开口对电机气隙谐波磁场的影响角度出发，通过分析不同槽开口下的电机模型，得到了谐波磁场以及转子中的涡电流随定子槽开口的变化情况，并精确计算了转子铁心与导条上的涡流损耗，进而探究了定子槽口宽与转子涡流损耗之间的关系。

1 电机负载时磁场的分析

负载时转子中的涡流损耗主要是由定子磁势谐波磁场以及由定子开槽引起的气隙磁导齿谐波磁场感生引起的。

1.1 定子绕组磁势谐波磁场

定子绕组磁势建立的谐波磁场计算如下［14］∶

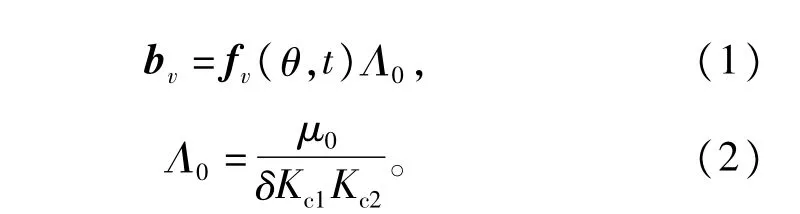
其中

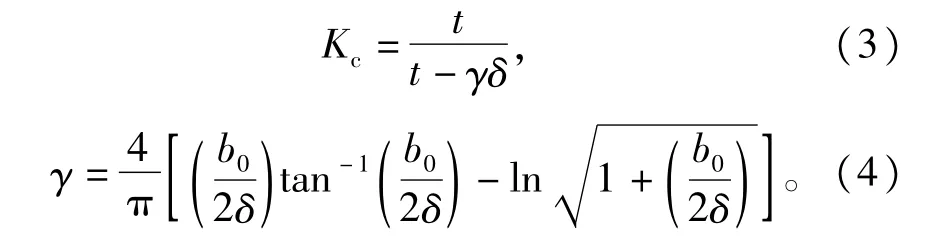
式中∶bv为定子绕组谐波磁场的磁密；fv（θ，t）为定子绕组谐波磁势；Λ0为气隙磁导直流分量；δ为电机气隙长度；μ0为真空的相对磁导率；b0为定子槽口宽；γ为系数；Kc1，Kc2分别为转子表面光滑定子有齿槽时的卡特系数和定子表面光滑转子有齿槽时的卡特系数。

定子绕组的磁势谐波分为相带谐波磁势及齿谐波磁势。当定子绕组每极每相槽数为整数时，磁势谐波中相带谐波极对数v为

v=（6k1+1）p，k1=±1，±2，±3…。 （5）

其中p为极对数。

定子绕组磁势谐波中齿谐波不随绕线排布所改变，其极对数vt为

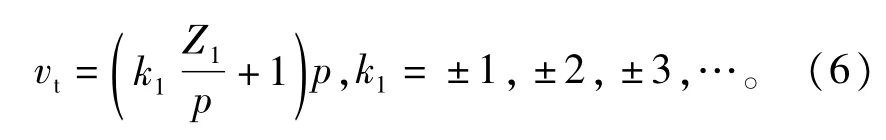
式中Z1为定子槽数。

1.2 定子气隙磁导齿谐波磁场b01=fp（θ，t）Λk1cosk1Z1θ。 （7）其中∶b01为定子气隙磁导齿谐波磁场的磁密；fp（θ，t）为主波合成磁势；Λk1为定子齿谐波磁导的幅值。

定子k阶齿谐波磁导的幅值表达式［14］为

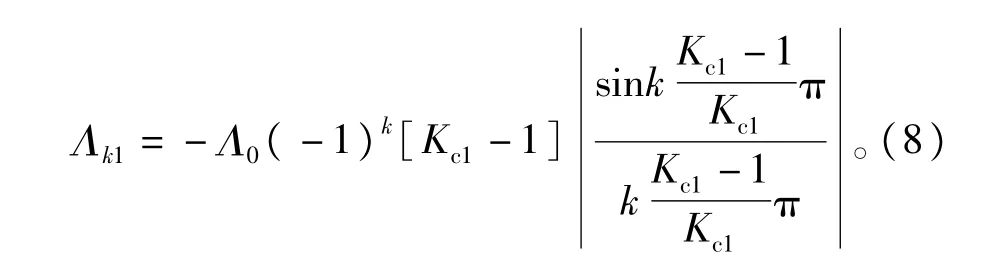
其中k=1，2，3…

定子绕组磁势谐波与定子磁导谐波均为空间谐波，频率均为ω1。定子磁导齿谐波与同阶定子磁势齿谐波具有相同的极对数和频率，二者只有相位不同，而在仿真中通过傅里叶分解得到的通常是二者合成后的幅值。也有文献称对于一阶齿谐波就是简单的二者幅值相加或相减，而其他各阶次则按照嵌放方式决定［7］。

分析式（1）～式（2）可知，气隙磁导不变部分与卡特系数成反比，而卡特系数与定子槽开口成正相关关系。所以槽开口增大，气隙磁导不变部分减小，定子磁势谐波磁场也随之减小。而分析式（7）～式（8）可知，随着定子槽开口增大，定子的一阶二阶齿谐波磁导将随之增大，所以其齿谐波磁场将随之增大。

2 二维有限元计算转子涡流损耗

转子中的涡流损耗包括转子铁心涡流损耗和转子导条中的涡流损耗。在传统解析法分析中考虑笼型转子绕组中的去磁效应，忽略了谐波在转子齿中产生的脉振损耗，只考虑转子表面损耗。本文使用二维有限元进行计算，考虑了整个转子铁心中的损耗，包括了表面、齿部及扼部。另外，传统解析法没有办法考虑电机中的磁路饱和、集肤效应以及涡流对磁场的削弱作用等影响因素。而使用有限元计算则可以充分考虑以上问题。

根据麦克斯韦方程组，列出二维场量表达式为

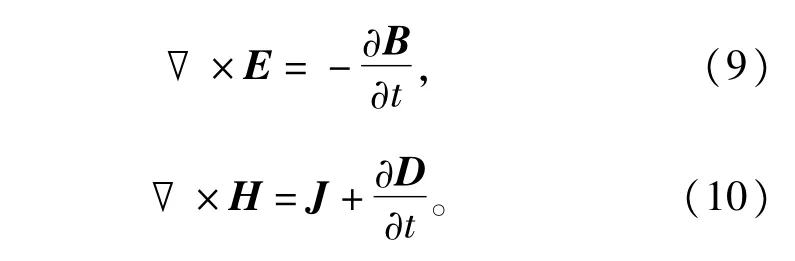
根据Poynting定理可以得到

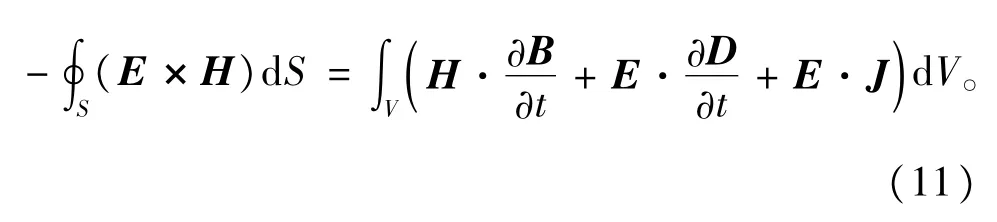
电机内部电磁场可近似认为是似稳电磁场，因此可以忽略位移电流的作用。并且由于铁心中的磁导率较大，所以式（11）右边第一项也可进行忽略。由此可以得到转子铁心或导条的涡流损耗计算公式［15］为

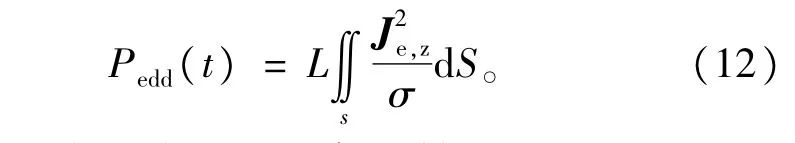
式中∶Je，z为转子铁心或导条的轴向涡电流密度；L为轴向长度；S为端面涡流区域的面积；Pedd（t）为涡流损耗。

3 仿真实验结果与分析

3.1 有限元模型的建立

本文仿真实验所采用的电机模型为∶2.2kW铸铝转子普通小型感应电机。电机转子采用直槽，其具体参数如表1所示。

电机的二维模型如图1所示。

为了表示清楚，图1给出的是电机1/4模型图，而在实际仿真计算中用的是全模型。

仿真实验中对定子槽开口Bs0在0到5.5mm之间每隔0.5mm取一个值，并特别地取了Bs0为 2.8mm的半闭口槽模型，总共建立了13个模型。并且为了研究气隙及转子中的电磁场特征，在气隙及转子中画了4条线，以便于分析计算。如图2、图3所示。

表1 电机主要参数Table1 Mainspecificationsofmotor

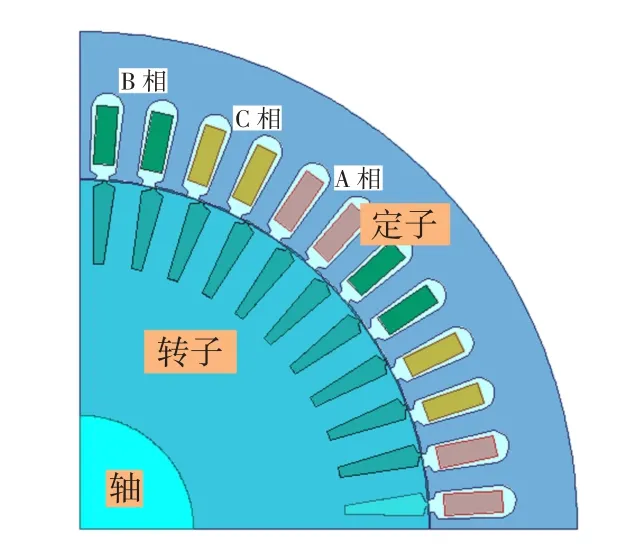
图1 电机的模型图Fig.1 Diagramofmotormodel

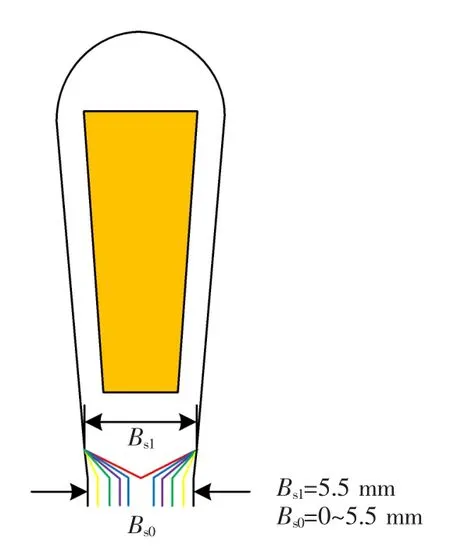
图2 改变定子槽口宽的图示Fig.2 Sketchofchangingthewidthofthestatorslot

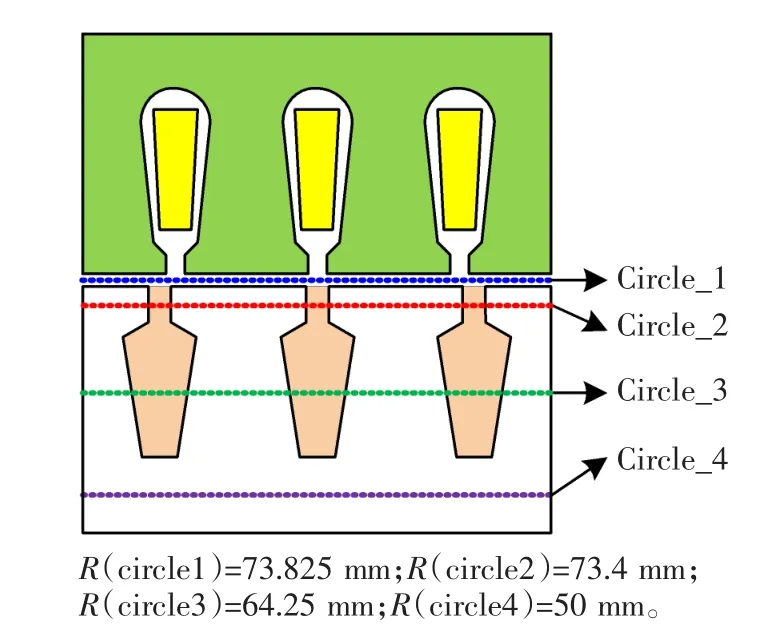
图3 气隙及转子中4条线的位置分布Fig.3 Distributionofthefourlinesinthe airgapandrotor

3.2 仿真结果与分析

3.2.1 磁场部分

由于磁场分布曲线类似，在此以原电机模型（定子槽开口为2.8mm的半闭口槽模型）为代表，给出其气隙与转子不同位置处的径向磁密的分布曲线。

图4分别是气隙中心线处、转子槽口处、槽高1/2处、扼部的磁密圆周分布。对比发现，转子扼部的磁密幅值最小，谐波最少；由于转子槽高1/2处的圆线上齿槽相邻，所以导致其磁密幅值波动最大、谐波最多。对气隙中的磁密作傅里叶分解可以得到气隙中的各次谐波分量。根据上述理论分析可知，谐波中主要成分是定子一阶、二阶相带谐波（-5和7次、-11和13次）、定子一阶、二阶齿谐波（-11和13次、-23和25次）。

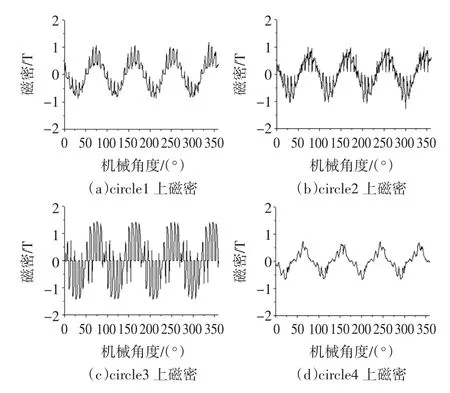
图4 Bs0=2.8mm时转子各部位的磁密分布Fig.4 Fluxdensitydistributionofairgapand rotorwhenBs0=2.8mm

图5描述的是不同定子槽开口下，气隙中心线即circle1上气隙磁密的各次谐波。其中-11次和13次的谐波最大并且其幅值随着定子槽开口的增大而增大，这是因为其叠加了定子的二阶相带谐波、定子磁势一阶齿谐波和磁导一阶齿谐波。而图中定子一阶相带谐波磁密的幅值随槽开口增大有逐渐减小的趋势，这与前文的理论推导是吻合。图中闭口槽磁密的幅值要小于开口槽，这可能与磁场的饱和有关。分析图5，可以发现，磁导齿谐波增长的幅值要比磁势谐波减小的幅值大的多。这将会导致随着槽口宽增大，总的谐波磁场有增大的趋势，这也表明转子中的涡流损耗可能会随定子槽口宽的增大而呈现增大的趋势。

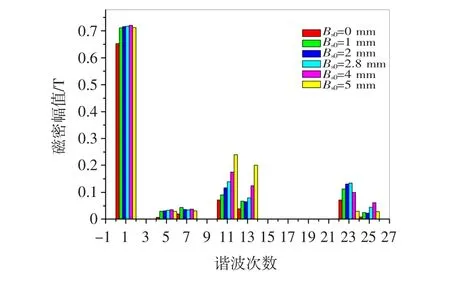
图5 不同槽开口气隙中心线上磁密各次谐波Fig.5 Harmonicsoffluxdensityintheairgap centerofdifferentslotopening

3.2.2 涡流部分

气隙磁场中的高次谐波在转子铁心及导条上感应产生涡流。对其仿真计算，得到如下结果。

图6为转子中的涡电流云图，可以看到转子表面以及导条中的涡电流密度比较大，而转子扼部基本上为零。图7（a）、图7（b）、图7（c）分别取自闭口槽、半开口槽及全开口槽电机在转子槽口曲线所得到的涡电流一周的分布图。由于线circle2处于齿槽相间槽口部，所以涡电流曲线波动幅度很大。对比3者可以发现，涡电流均呈现八极对称分布，并且随着槽开口增大涡电流的幅值也逐渐增大。此仿真结果与上文的推论保持一致。

图8为转子槽高1/2处画线上（circle3）和扼部画线上（circle4）中的涡电流随圆周分布图。线circle3上为齿槽相邻，由图8（a）可以看到，不同定子槽开口模型中circle3上的涡流曲线基本重合，其中导条中的涡流密度要比齿中的大很多，并且几乎所有导条中涡流密度幅值都随槽开口的增加而略微增大。图8（b）中除了闭口槽的幅值相对较小外，其他槽型涡电流密度的波形也基本重合，这说明槽开口对于转子齿中及扼部的涡电流密度的影响很小。综合图6～图8，转子铁心中的涡电流密度随着从槽口到扼部的深人幅值越来越小。这表明只有少量谐波磁场才能渗透进人转子齿部，暗示着转子铁心中的涡流损耗主要集中在转子表面。

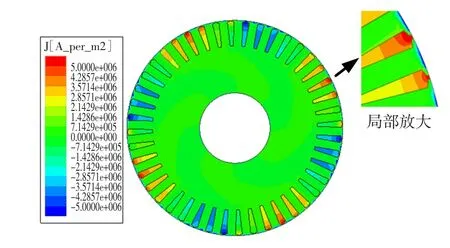
图6 转子及导条的涡电流云图Fig.6 Nephogramofeddycurrentinrotorandbars

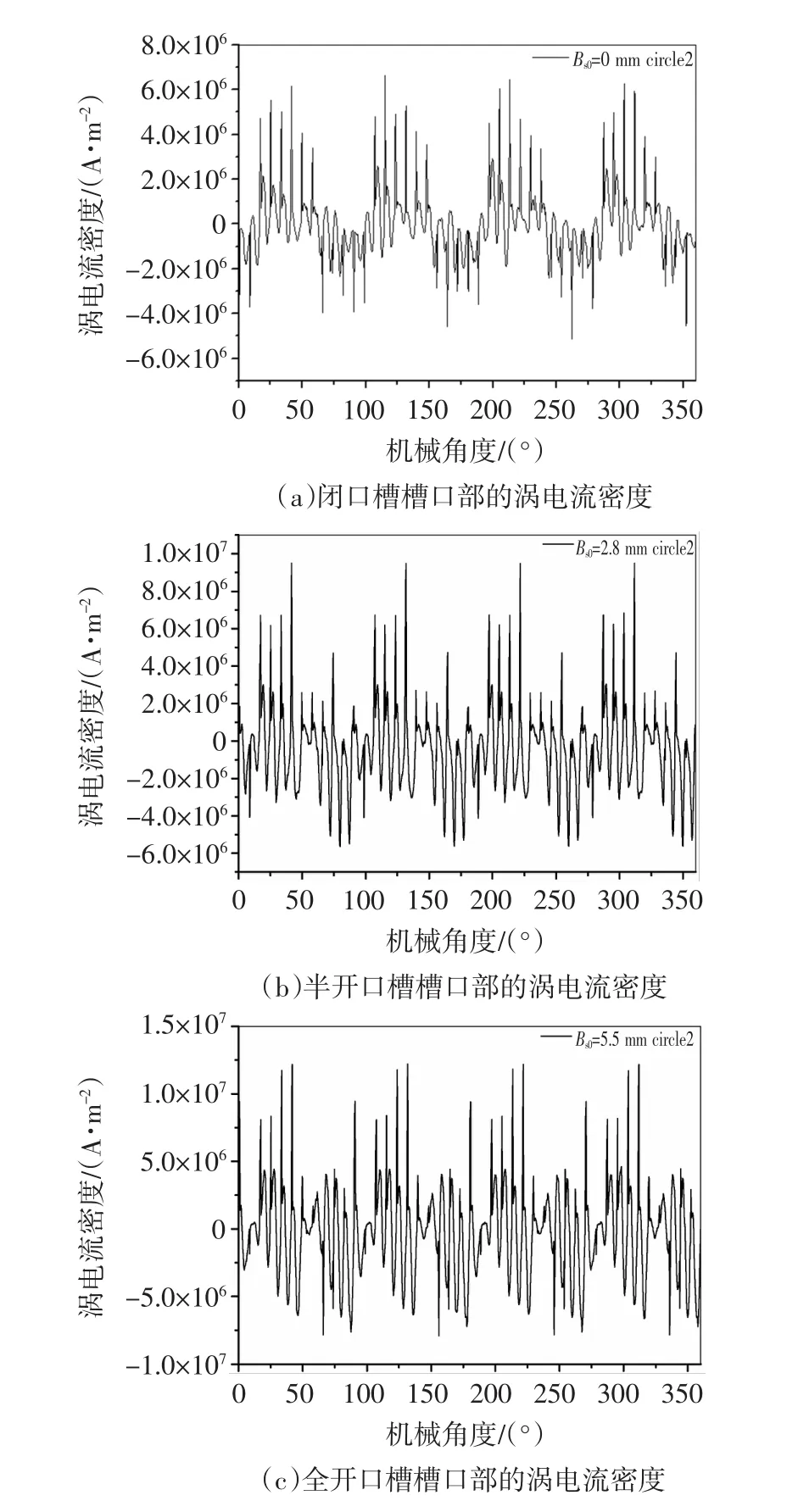
图7 各个槽型槽口部的涡电流密度Fig.7 Eddycurrentdensityinslotnotchesof differentslotopeningmodels

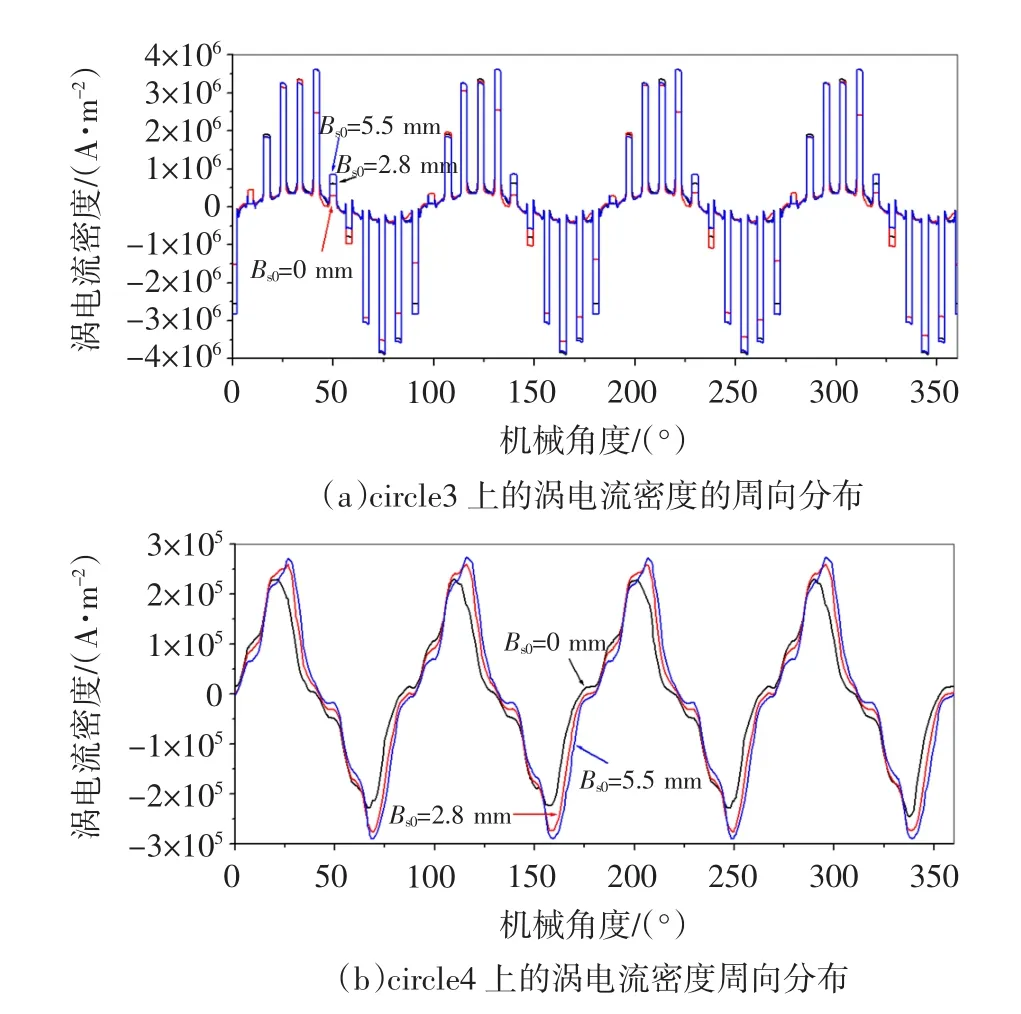
图8 各个槽型circle3、circle4的涡电流分布Fig.8 Eddycurrentdistributionincircle3and circle4ofdifferentmodels

转子导条中的电流频率小，周期大，如图9（a）所示，此电机模型稳定后一个周期为420ms。以定子为闭口槽时为例，对一个周期的导条电流进行傅立叶分解得到频率为2.38Hz幅值为199.51A的基波电流和各次谐波电流，如图9（b）所示。

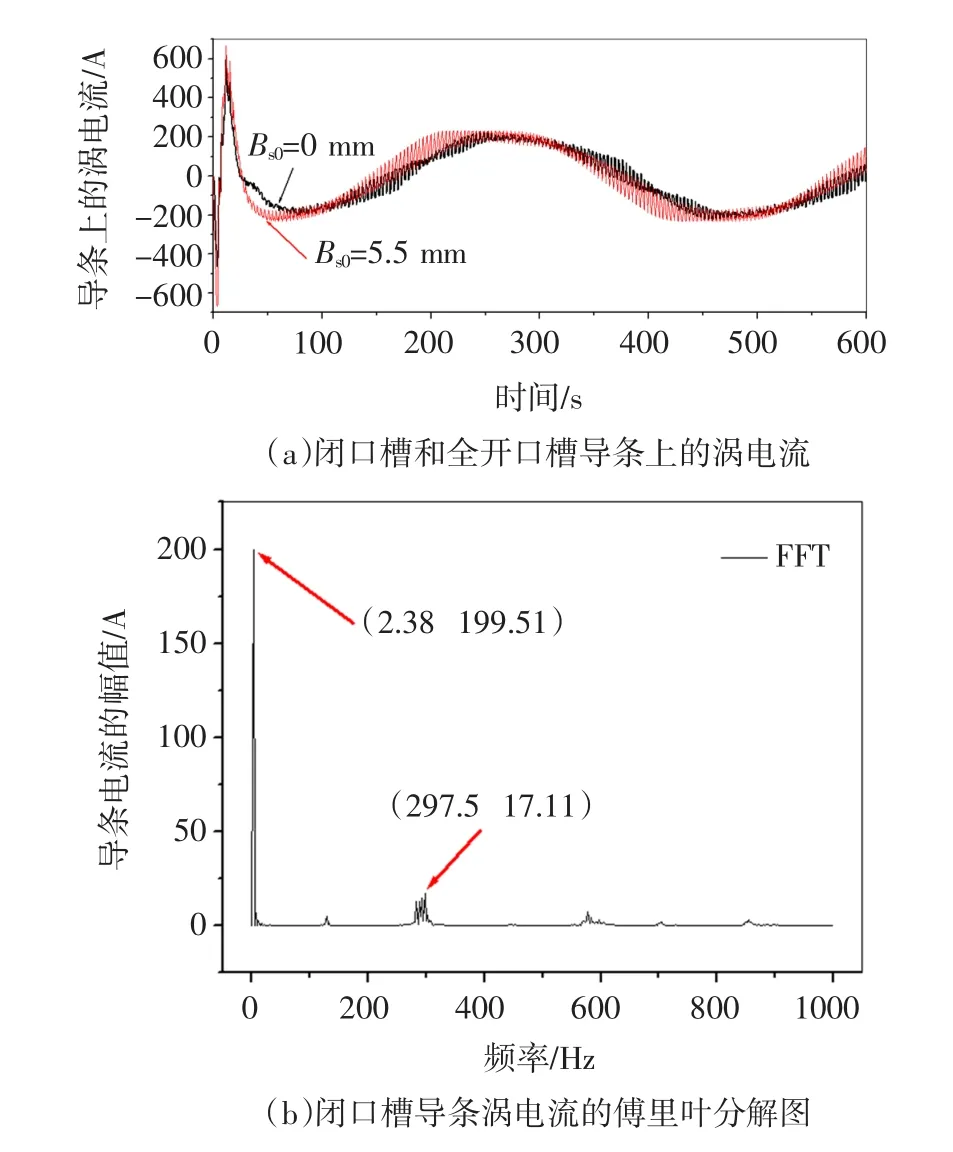
图9 导条上的涡电流与闭口槽导条电流的傅里叶分解图Fig.9 EddycurrentinbarsandFourierdecompositionof barcurrentinclosedslotmodel

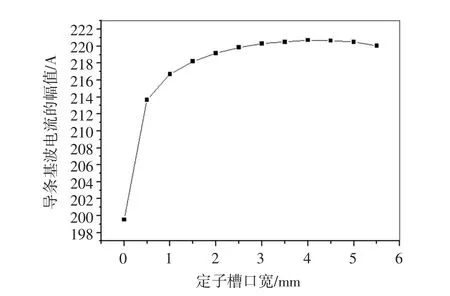
可以看到，导条电流中的谐波较少且幅值较小，这表明导条中的损耗主要为铝耗。图10为对不同槽口宽导条电流进行傅里叶分解所得到的基波电流随槽口宽变化的图形。可以看出，随着槽口宽不断增大基波电流的幅值也不断增大，并且在电机从闭口变为开口时，电流增长的速率很快，在定子将要变成全开口时，增长速率变得缓慢。

3.2.3 损耗部分

转子上的损耗包括转子铁心和转子导条上的涡流损耗。运用上述二维有限元的方法对各个模型的涡流损耗进行计算，可以得到如下结果。

图11描述的是定子闭口、半开口、全开口槽型时对应的转子铁心单位长度上的涡流损耗。可以看到，在70ms电机稳定后，闭口槽的涡流损耗幅值最小，脉动最小；而全开口槽的幅值最大，脉动最大。这和电磁场的涡电流密度，磁密的结果是一致的。取各个槽型稳定后转子铁心涡流损耗单位周期内的有效值得到图12，并对其进行插值法函数拟合，可以得到转子铁心涡流损耗随定子槽开口变化的函数关系。可以看到，转子铁心上的涡流损耗随定子槽开口的增大而增大，并且服从二次函数的增长关系。

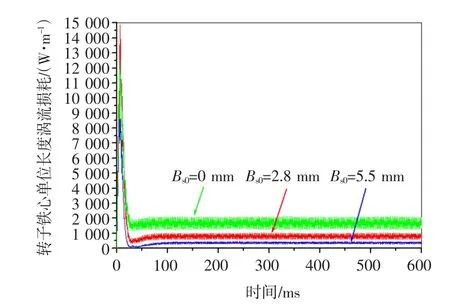
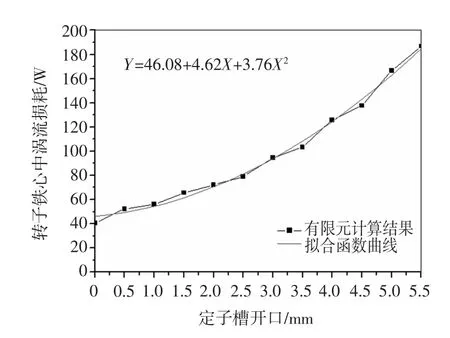
图12 转子铁心涡流损耗随槽开口变化曲线Fig.12 Rotorcoreeddycurrentlossvaries withslotopening

图13描述的是两对极下的22根转子导条每根导条单位长度上对应的损耗。很明显可以看出，闭口槽损耗的幅值最小波动最小，开口槽的幅值最大脉动最大，这与导条的涡电流密度结果是一致的，其损耗的数值特征类似于转子铁心上的损耗。分析图13，还可以看出，每对极下的不同导条上的损耗是不同的，并且以一对极作为一个周期呈明显的周期分布。

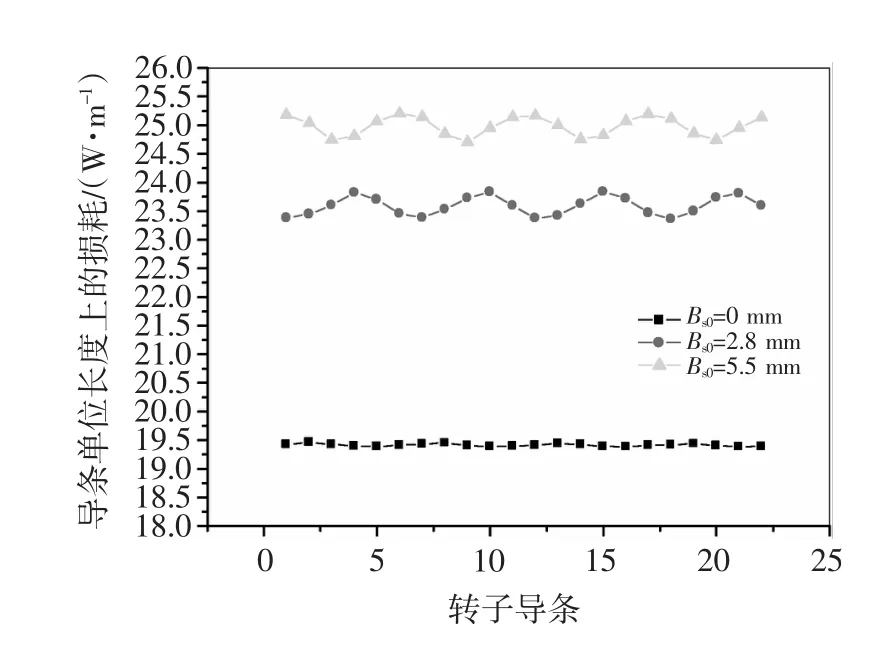
图13 两对极下的导条单位长度上损耗Fig.13 Lossofunitlengthinbarsoftwopairsofpoles

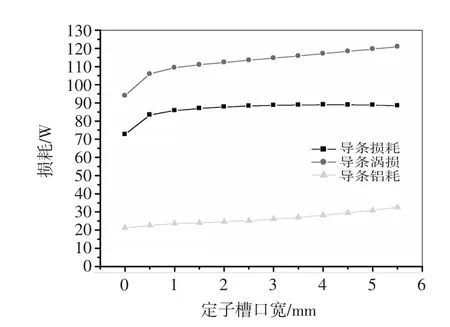
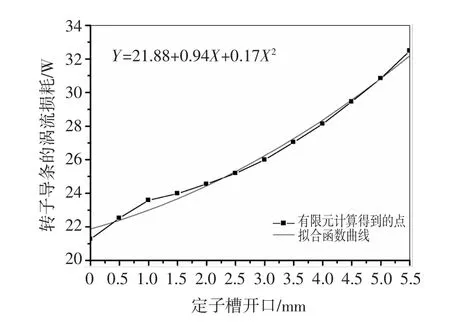
图14描述的是对应于各个定子槽口宽转子导条上的3种损耗。这里的损耗是指所有导条上（共44根）的损耗之和。导条铝耗是指由转子导条中的基波感应电流所产生的损耗。导条涡损是指导条中的谐波电流所产生的损耗。导条损耗指导条中涡电流引起的总的损耗，是涡损和铝耗之和。明显看出，导条中的各个损耗也是随着定子槽开口的增大而增大。对导条涡流损耗随槽开口变化的曲线进行函数拟合，可以得到与转子铁心类似的函数关系，如图15所示。导条上的涡流损耗对于定子槽口宽也呈现二次函数变化的增长趋势。

4 结论

本文通过理论分析了定子槽开口变化对负载时电机转子中电磁场的影响，并对2.2kW的小型铸铝感应电机进行了二维有限元仿真计算，探讨了不同定子槽开口下电机气隙中的磁场以及转子中各部分涡电流的分布情况，最后通过函数拟合的方法得到了对于该种型号电机定子槽开口与转子涡流损耗之间的定量变化关系。通过仿真的结果可以得到以下结论∶

1）气隙谐波磁场中11次和13次谐波幅值最大并使得总的谐波磁场随着定子槽开口增大而增大；

2）相较于转子齿中与转子扼中，转子铁心表面的涡电流密度最大，其幅值随定子槽开口的增大也有明显的增大趋势；

3）转子铁心及转子导条中的涡流损耗也随定子槽开口的增大而增大，并且对于此型号的电机其增长趋势可以用二次函数来进行拟合。本文的研究对于电机设计以及工程计算转子上的损耗具有一定的参考意义。

∶

［1］李军丽.三相笼型异步电动机负载杂散损耗的测试方法［J］.电机与控制应用，2009，36（4）∶44-48. LIJunli.Standardmethodsforstray-loadlossofthree-phasecage asynchronousmotors［J］.ElectricMachine＆ControlApplication，2009，36（4）∶44-48.

［2］ZHAONannan，ZHUZQ，LIUWei.Rotoreddycurrentlosscalculationandthermalanalysisofpermanentmagnetmotorandgenerator［J］.IEEETransactionsonMagnetics，2011，47（10）∶4199-4202.

［3］李伟力，管春伟，郑萍.大型汽轮发电机空实心股线涡流损耗分布与温度场的计算方法［J］.中国电机工程学报，2012，32（增）∶264-271. LIWeili，GUANChunwei，ZHENGPing.Caliculationmethodof eddycurrentlossdistributionandtemperaturefieldformixedhollowandsolidstrandsinlargeturbo-generator［J］.Proceedingsof theCSEE，2012，32（S）∶107-113.

［4］孔晓光，王凤翔，邢军强.高速永磁电机的损耗计算与温度场分析［J］.电工技术学报，2012，27（9）∶166-172. KONGXiaoguang，WANGFengxiang，XINGJunqiang.Losses calculationandtemperaturefieldanalysisofhighspeedpermanent magnetmachines［J］.TransactionsofChinaElectricalSociety，2012，27（9）∶166-172.

［5］周凤争，沈建新，林瑞光.从电机设计的角度减少高速永磁电机转子损耗［J］.浙江大学学报∶工学版，2007，41（9）∶1587-1591. ZHOUFengzheng，SHENJianxin，LINRuiguang.Reductionof rotorlossinhigh-speedpermanentmotorsbydesignmethod［J］. JournalofZhejiangUniversity∶Engineeringscience，2007，41（9）∶1587-1591.

［6］DAISUKEHiramatsu，TADASHITokumasu，MASAFUMIFujita，etal.Astudyonrotorsurfacelossesinsmall-to-mediumcylindricalsynchronousmachine［J］.IEEETransactionsonEnergyConversion，2012，27（4）∶813-821.

［7］常正峰，黄文新，胡育文，等.基于二维解析法的光滑表面实心转子感应电机附加损耗的研究［J］.中国电机工程学报，2007，27（21）∶83-88. CHANGZhengfen，HUANGWenxin，HUYuwen，etal.Research onstraylossofsmoothsurfacesolidrotorinductionmotorbasedon 2Danalyticalapproach［J］.ProceedingsoftheCSEE，2007，27（21）∶83-88.

［8］YANHUIGao，TATSUNORISanmaru，GENKIUrabe，etal.E-valuationofstrayloadlossesincoresandsecondaryconductorsof inductionmotorusingmagneticfieldanalysis［J］.IEEETransactionsonMagnetics，2013，49（5）∶1965-1968.

［9］ANTUNESOJ，BASTOJPA，SADOWSKIN，etal.Torquecalculationwithconformingandnonconformingmovementinterface ［J］.IEEETransactionsonMagnetics，2006，42（4）∶983-986.

［10］TAKAHASHIY，KAIMORIH，KAMEARIA，etal.Convergenceaccelerationinsteadystateanalysisofsynchronousmachinesusingtime-periodicexpliciterrorcorrectionmethod［J］. IEEETransactionsonMagnetics，2011，47（5）∶1422-1425.

［11］HUNGVuXuan，LAHAYED，HOEIJMAKERSMJ，etal. Studyingrotoreddycurrentlossofpmmachinesusingnonlinear femincludingrotormotion［C］//2010XIXInternationalConferenceonElecticalMachines-ICEM，Sept6-8，2010，Rome，Italy.2010∶1-3.

［12］LIJian，CHOIDa-woon，SONDong-hyeok，etal.Effectsof MMFharmonicsonrotoreddy-currentlossesforinner-rotorfractionalslotaxialfluxpermanentmagnetsynchronousmachines ［J］.IEEETransactionsonMagnetics，2012，48（2）∶839 -842.

［13］梁艳萍，张建涛，索文旭，等.双屏蔽复合转子电机涡流损耗分析［J］.中国电机工程学报，2009，29（24）∶78-83. LIANGYanping，ZHANGJiantao，SUOWenxu，etal.Eddy currentlossanalysisofdouble-canscomposite-rotormotor［J］. ProceedingsoftheCSEE，2009，29（24）∶78-83.

［14］陈永校，诸自强，应善成，等.电机噪声的分析与控制［M］.第一版.浙江∶浙江大学出版社，1987.

［15］HUNGVuXuan，DOMENICOLahaye，HENKPolinder，etal. Influenceofstatorslottingontheperformanceofpermanent-magnetmachineswithconcentratedwindings［J］.IEEETransactions onMagnetics，2013，49（2）∶929-938.

（编辑∶刘琳琳）

Influenceofstatorslotopeningsonloadedrotoreddycurrentloss

BAOXiao-hua，LIANGNa，FANGYong，WANGHan-feng
（SchoolofElectricalEngineeringandAutomation，HefeiUniversityofTechnology，Hefei230009，China）

∶Inordertocalculatetheeddycurrentlossinrotorofinductionmotorpreciselyandinvestigate theinfluenceofstatorslottingontheloss，asmallinductionmotorwithaluminumcastingrotor，which has4polepairsanditsratedpoweris2.2kW，wasanalyzedindetail.Therelationshipbetweenairgap harmonicmagneticfieldandstatorslotopeningwasdiscussedbythetheoreticalanalysisofharmonicmagneticfieldininductionmotor.Distributionsofmagneticfielddensityandeddycurrentindifferentpositionofrotorwerealsoobtainedbyusingtwo-dimensionalfiniteelementmethod.Finally，throughestablishingmotormodelswithdifferentstatorslotopening，comparativeanalysiswascarriedoutontheeddycurrentlossinrotorcoreandbars.Simulationresultshowsthat，boththevalueofharmonicfieldinairgap andeddycurrentdensityinrotorsurfaceincreasewithstatorslotopening.Andtheeddycurrentlossof rotorcoreandbarsalsoincreasewithit，whichrisingtendencyplaysoutwithaquadraticfunctionexpression.

∶inductionmotors；slotopenings；harmonicfield；eddycurrentloss；2-Dfiniteelement

∶TM343

∶A

∶1007-449X（2015）11-0017-08

∶2014-07-14

∶国家自然科学基金（51177033，51377039）

∶鲍晓华（1972—），男，博士，教授，研究方向为电机设计理论和技术、电机电磁场理论分析及计算；

梁 娜（1993—），女，硕士研究生，研究方向为电机电磁场分析与计算；

方 勇（1989—），男，硕士研究生，研究方向为电机电磁场计算；

王汉丰（1991—），男，硕士研究生，研究方向为电机设计理论、电机电磁场计算。

∶鲍晓华

DOI∶10.15938/j.emc.2015.11.003