基于ECDSA的智能卡软件设计与实现
白永祥
(1.渭南职业技术学院 陕西 渭南 714000;2.西北大学 信息科学与技术学院,陕西 西安 710127)
数字签名是公钥密码体系重要的应用,它在实现身份认证、数据完整性、不可抵赖性等方面都有重要应用,是实现电子交易安全的核心技术之一。目前,大部分的数字签名软件几乎都是采用RSA作为标准算法,但随着计算机性能和解密技术的不断提高,RSA的安全性受到了不同程度的攻击,为了提高RSA的安全性,不断的增加钥密长度,造成了计算机处理工作量的增大,从而影响了加密解密的速度。
椭圆曲线是一门古老而且内容丰富的数学分支,1985年,Miller和Koblitz各自独立地提出椭圆曲线公钥密码学(Elliptic Curves Cryptography ECC),同 RSA算法相比较,ECC具有密钥长度短,占用计算机存储空间少,计算机处理速度快等特点[1],同时椭圆曲线还具有丰富多样的类型,所有这些都非常适合密码学的应用。近年来,专家学者都在不加深椭圆曲线在密码学方面的应用研究。
1 椭圆曲线密码系统
1.1 ECC原理概述
椭圆曲线密码体制的安全性基于有限域上椭圆曲线离散 对 数 问 题 (Elliptic Curve Discrete Logarithm Problem,ECDLP)的难解性。这种密码体制目前还没有找到解决此问题的亚指数时间算法,因而它具有一些其他公钥密码体制无法比拟的优点。
所谓椭圆曲线就是在有限域Fq上的Weierstrass方程式:
应用于密码学中的椭圆曲线是由满足该方程式的所有点(x,y)及一个无限远点所形成的集合,常用于应用的椭圆曲线有3种:
1)实数域上的椭圆曲线:y2=x3+ax+b(a,b∈R,且满足4a2+27b3≠0);
2)有限域 GF(p)上的椭圆曲线:y2=x3+ax+b(mod p),a,b,x,y∈{0,1,…,p-1};
3)有限域 GF(2m)上的椭圆曲线:y2+xy=x3+ax2+b,a,b,x,y∈GF(2m)。
1.2 椭圆曲线上点的群运算法则
给定一条Fq上的椭圆曲线E,及其上的任意两点P和Q,连接P和Q的直线与E交于第3个点-R,由于-R和无穷远点O可决定一直线,该直线与E交于一个交点R定为P与Q的和,记为P+Q。可以证明这样定义E上点的加法后,就使E成为一个Abel群。具体的运算法则如下:
设 P=(x1,y1),Q=(x2,y2) 为实数域上椭圆曲线上任意两点,且P≠O≠Q,则有椭圆曲线方程:y2=x3+ax+b
则两点加法的运算规则如下:
1)当 P≠Q 时,P+Q=R(x3,y3),如图 1 所示;
2)当 P=Q 时,P+Q=R(x3,y3),如图 2 所示;
3)当 x1=x2时,P+(-P)=(x1+y1)+(x1,-y1)=O,如图 3 所示;
定义:P+O=O+P=P。

图 1 P+Q=R(x3,x3)Fig.1 P+Q=R(x3,x3)

图2 P+Q=P+P=2P=RFig.2 P+Q=P+P=2P=R

图 3 P+(-P)=OFig.3 P+(-P)=O
由于椭圆曲线加密算法具有密钥长度短,占用存贮空间少、灵活性好等特点,所以椭圆曲线加密算法相对于RSA加密算法具有绝对的优势,目前已成为非对称密钥加密体制中的研究热点。
1.3 椭圆曲线加密解密算法
1.3.1 密钥生成
参与者Alice发送信息给接收者Bob,Alice需要完成下述过程[2]:
1)Alice 随机选取一个整数 dA∈[1,n-1];
2)然后 Alice计算 QA=dAP;
3)Alice的公钥为点 QA;
4)Alice的私钥为整数 dA。
对于Bob也要做同样的工作,具体过程如下:
1)Bob 随机选取一个整数 dB∈[1,n-1];
2)然后 Bob计算 QB=dBP;
3)Bob 的公钥为点 QB;
4)Bob的私钥为整数 dB。
1.3.2 加密、解密方案
现在假设Bob要发送信息给Alice,则Bob的加密过程如下:
1)找出 Alice的公钥 QA;
2)将信息M表示为一个域元素m∈Fq;
3)随机选取一个整数 k∈[1,n-1];
4)计算点(x1,y1)=kP;
5)计算机点(x2,y2)=kQA,若 x2=0,则返回第 3 步;
6)计算 c=m·x2;
7)将已加密数据(x1,y1,c)发送给 A。
Alice收到密文(x1,y1,c)后的解密过程如下:
1)计算点(x2,y2)=dA(x1,y1),得出 x2∈Fq;
2)计算 m=c·x-12,得出信息 M。
1.4 椭圆曲线数字签名算法(ECDSA)
1998年,椭圆曲线数字签名算法(ECDSA)成为ISO标准,ECDSA相对传统签名算法具有速度快、强度高、签名短等优点,其应用也逐渐广泛了,例如Windows系列操作系统25位的CD-Key中就使用了椭圆曲线签名算法[3]。ECDSA的工作原理与大多数签名算法类似,都是使用私钥进行签名,公钥进行验证。
下面给出的ECDSA方案是基于IEEE P1363标准草案给出的,具体算法描述过程如下:
假设Alice要向Bob发送签名后的消信M,Alice首先确定安全Hash函数,定义椭圆曲线也就是确定参数T=(p,a,b,G,n,h),然后建立密钥对(dA,QA),其中 dA是私钥,QA=dAG 是公钥,并向用户Bob发送Hash函数,椭圆曲线参数和公钥QA。设Alice要对信息签名后再发给用户Bob那么Alice要完成下述步骤:
1)将待发送信息M转化为比特串;
2)计算信息M的消息摘要:e=H(M);
3)随机选取整数 k∈[1,n-1];
4)计算点(x1,y1)=kP;令 r=x1(mod n),若 r=0,返回第 3)步;
5)Alice 应用自己的私钥 dA计算 s=k-1(e+rdA)(mod n),若s=0,则返回第 3)步;
6)Alice 将信息 M 和签名(r,s)发给 Bob。
ECDSA签名验证:当Bob收到Alice对信息M的签名(r,s),需要验证是否为Alice所签,则Bob要完成下述过程:
1)找出 Alice的公钥 QA;
2)计算 Hash值 e=H(M);
3)计算 s-1mod n;
4)计算 u=s-1e mod n 和 v=s-1r mod n;
5)计算点(x1,y1)=uP1+vQA;
6)当且仅当x1mod n=r时,Alice对信息M的签名被Bob认可。
2 Hash函数
2.1 Hash函数定义
Hash函数又称杂凑函数、消息摘要或消息指纹,它是把一段任意长度的比特串作为输入,通过某种算法产生一个固定值为n的输出比特串,称其为消息的杂凑值[4]。
h:{0,1}*→{0,1}n,m→h(m)
Hash函数其实就是一种将无限多个元素映射到有限个元素的一种特殊的数学函数。它是把任意长度的输入通过散列算法变换成一个固定长度的输出,称该输出为散列值或消息指纹,这种转换是一种压缩映射,也就是说散列值所占的空间远远小于输入的空间。Hash函数在现代密码学中具有重要的作用。
2.2 Hash函数的安全性
在数字签名中往往先使用杂凑函数对消息m实施 “压缩”运算,接着对消息m的杂凑值实施签名,这样既起到了保密作用,又提高了加密速度。对于在数字签名中使用的杂凑函数,要求它们具有更强的安全性能。常用的Hash算法有MD5、SHA-1和SHA-2等,而随着计算机运算速度的不断提高和解密技术的改进,这些算法都不同程度的受到安全性威胁。在2005年2月,王晓云以及他的同事使用差分路径攻击,只用了2的69次方次就完成了SHA-1的循环碰撞周期。SHA-1和SHA-2使用了相同的处理引擎,在处理消息文本时,对SHA-1的成功攻击行为会影响到SHA-2的安全[5]。
2012年10月,美国NIST选择了Keccak算法作为SHA-3的标准算法,Keccak拥有良好的加密性能以及抗解密能力。Keccak采用了创新的的“海绵引擎”散列消息文本,它设计简单,方便硬件实现。Keccak已可以抵御最小的复杂度为2n的攻击,它具有广泛的安全边际,至目前为止,第三方密码分析已经显示出Keccak没有严重的弱点[6]。
3 智能卡
智能卡是以IC卡(Integrated Circuit Card)技术为核心,以计算机和通信技术为手段,一般制作在给定大小的塑料卡片上,表面封装了集成电路芯片,用于存储和处理数据,它由塑料基片、接触面、集成电路三部分组成。智能卡已广泛应用于金融、电信等领域。椭圆曲线密码系统是目前已知的所有公钥密码体制中能够提供最高比特强度的一种公钥体制[7]。我们常把智能卡分成接触卡和非接触卡两类,其中接触卡主要是存储卡,由于卡内资源有限,内存较小,而椭圆曲线密码系统对时间和空间资源要求不高,刚好适用于智能卡,这样不仅能大大提高智能卡的应用水平,而且还大大拓宽智能卡的应用领域。
4 软件设计
4.1 概要设计
软件功能包括登录密码验证、密钥设置、数字签名及检验,如果密码输入错误,为了保护用户账号安全,最多只有三次机会,超过三次输入,智能卡便会死锁。具体应用流程如图4所示。
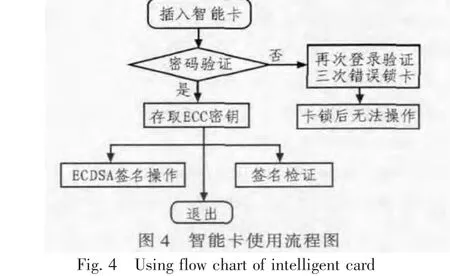
4.2 数字签名设计
由于C++具有代码效率高等优点,所以数字签名使用VC++6.0开发环境进行实现[8],ECDSA主要过程代码如下:
KEYPAIR_GE Random_key;
BIGINT x_value, k_value, signature_value, r_value;
BIGINT temp,quotient;
BIGINT random_k;
BIGINT key_value, point_order, u_value;
INDEX i, count;
Copy(&ECDSA_k, &Random_key,private_key);
Print_field (“given random number k= ”,&random_key,private_key);
/*computer k*G/
EC_multiple (&random_key,private_key,&public_curve ->pnt,&random_key);
/*display public key*/
Printf(“k*G= ”);
Print_point(“”,&random_key,public_key);
/*computer r=k*G(x) mod n*/
field_to_int(&public_curve->pnt_order,&point_order);
field_to_int(&random_key,public_key,c,&x_value);
int_div(&x_value,&point_order,"ient,&r_value);
int_to_field(&r_value,&signature->r);
/*computer s=k^-1(e+dr) mod n*/
4.3 数字签名检验
EC_point temp1, temp2, Verify;
BIGINTr_value, s_value;
BIGINT temp, quotient,h1,h2;
BIGINT check_value,point_order;
INDEX I,count;
FIELD_Ph1_field,h2_field;
/*computer inverse of second signature_value*/
Field_to_int(&public_courve->pnt_order,&point_order);
Field_to_int(&signature->s,&temp);
Mod_inv(&temp,&point_order,&s_value);
/*computer elliptic curve multipliers:h1=hash-3*s,h2=c*/
int_multiple(hash_value,&s_value,&temp);
int_div(&temp,&point_order,"ient,&h1)
int_to_field(&h1,&h1_field);
field_to_int(&signature->r,&r_value);
int_multiple(&s_value,&r_value,&temp);
int_div(&temp,&point_order,"ient,h2);
int_to_field(&h2,h2_field);
/*find hidden point from public data*/
EC_multiple (&h1_field,&public_curve ->pnt,&temp1,&public_curve);
EC_multiple (&h2_field,sigmature_point,&temp2,&public_curve->curve);
EC_add(&temp1,&temp2,&Verify,&public_curve->crv);
5 软件仿真
我们使用VC++6.0开发环境,它不但能快速建立Windows界面,且能使用Crypto++代码,使开发时间大大缩短,软件运行主界面如图5所示。

软件主界面分为3个部分:
1)主菜单部分:IC卡功能、数字签名、软件设置及帮助功能,IC卡用户名及资料只能在正确登录后才能显示出来。
2)数字签名部分:有3个分页选项,分别是数字签名生成、签名验证及记录IC卡处理过程的日志信息,方便用户以后查询。
3)IC卡设置功能按钮部分:有关IC卡存取等常用功能按钮,另外还有选项设定功能,用户可以修改一些常用选项。右上角的彩色IC卡表明目前IC卡正确联机使用,否则显示为灰色。
6 结 论
基于Crypto++库代码设计了一个在实验室仿真的ECDSA签名软件,距离实际应用还有大量后续工作要深入研究,目前,国内外有许多密码研究中心在这方面已经取得了可喜的成绩,甚至有成型的芯片出现,所有这些都预示着在不久的将来,ECC将会替代RSA成为公钥密码系统的标准。
[1]胡向东,魏琴芳,胡蓉.应用密码学[M].北京:电子工业出版社,2011.
[2]王学理,裴定一.椭圆与超椭圆曲线公钥密码的理论与实现[M].北京:科学出版社,2006.
[3]Stallings W.Cryptography and network security principles and practice,fifth edition[M].北京:电子工业出版社,2011.
[4]冯登国.密码学原理与实践[M].2版.北京:电子工业出版社,2005.
[5]JoséR.C.Cruz, Keccak:The New SHA -3 Encryption Standard[J].2013, 5(7):45-55.
[6]杨皇中.椭圆曲线密码系统软件实现技术之探讨[J].资讯安全通信,2005,11(1):15-25.YANG Huang-zhong.Software implementation technology of elliptic curve cryptosystem[J].Journal of Information Security Communication,2005,11(1):15-25.
[7]吴世忠,祝世雄.应用密码学协议、算法与C源程序[M].北京:机械工业出版社,2010.
[8]张惟淙,杨中皇.结合Java的ECDSA数位签章软件设计与实现[M].台湾:高雄师范大学出版社,2005.

