一种改进的多值属性模式聚类算法

王珊珊 梁同乐



一种改进的多值属性模式聚类算法

王珊珊1梁同乐2

（1.广东轻工职业技术学院 2.广东邮电职业技术学院）

pCluster算法是面向多值属性数据的聚类算法，能识别出多值属性间的相似性。针对模式聚类算法pCluster效率低的问题，提出pCluster的改进算法。实验证明，该改进算法能更高效地获得预期聚类结果。

关联规则；多值属性；模式聚类

0　引言

实体属性的关联规则挖掘是数据挖掘研究的重要方向之一，其目的在于发现数据实体各属性间隐藏的聚类关系。这种关系具有切实的实践意义，广泛应用于医疗数据分析、商业信息推广和科学实验结果评价等领域。

实体的属性分为布尔型属性和多值属性。多数学者着重于布尔型属性关联规则算法的研究，而多值属性关联规则发掘的相关文献相对较少。多值属性关联规则由Srikant R和Agrawal R等于1996年提出[1-2]。挖掘多值属性关联规则的算法，通常将每个属性值范围映射为布尔型属性，然后用布尔型属性的挖掘算法进行关联规则发现，如Apriori算法。但这会出现2个问题：一是多值属性转化为布尔型属性时导致的数据量迅速膨胀；二是如何量化多值属性的取值范围，区间太窄可能造成对应的支持度过低，区间太宽则会出现可信度无法达到阈值的情况。目前，也有一些算法无需将多值属性向布尔型属性转换[3-6]，但这些算法要求庞大的内存空间，以满足特殊数据结构存储及操作的需要。同时值得注意的是，维度效应对聚类分析的影响[7]。高维数据分群聚类时，由于数据集的复杂度较高，因此聚类的结果通常带有不确定性[8]。另外，一些相关研究探讨了高维子空间中群的发现[9-11]，然而这些聚类分群法大都是以物理距离作为相似度的计算基础，在某些情况下这种计算相似度的方式并不合适，例如基因序列中基因对反应的聚类，医疗数据中疾病属性值关联性的分析，这些数据往往需要在高维数据空间中寻找具有相关联意义的部分，进而进行分析。基于以上需求，模式聚类的概念逐渐在这些应用领域发挥优势，越来越多的学者开始关注应用模式聚类的概念进行子空间分群[12-14]。

Wang Haixun等在2002年提出了pCluster聚类算法[15]，不同于以往的聚类算法，其更加关注广泛意义上的属性子集相似模式，从而发现属性间的关联关系。本文提出的pCluster优化算法，致力于提高pCluster聚类算法的收敛速度。

1　相关研究介绍

多数聚类算法是基于距离挖掘相似类别的成员，即通过发现对象在子空间内距离的相近程度来度量。然而，在某些特定的数据集中，相同的簇成员不体现在对象间距离的相近，而是存在一种模式上的相似性。

图1表示有3个对象10个属性的数据集。在这3个对象中并不存在明显的相似模式，但如果将其中部分属性分离开，就可清晰地看到其中的相似性。例如查看属性集合｛,,,,｝，如图2所示，可以直观地看到它们之间的相似关系。

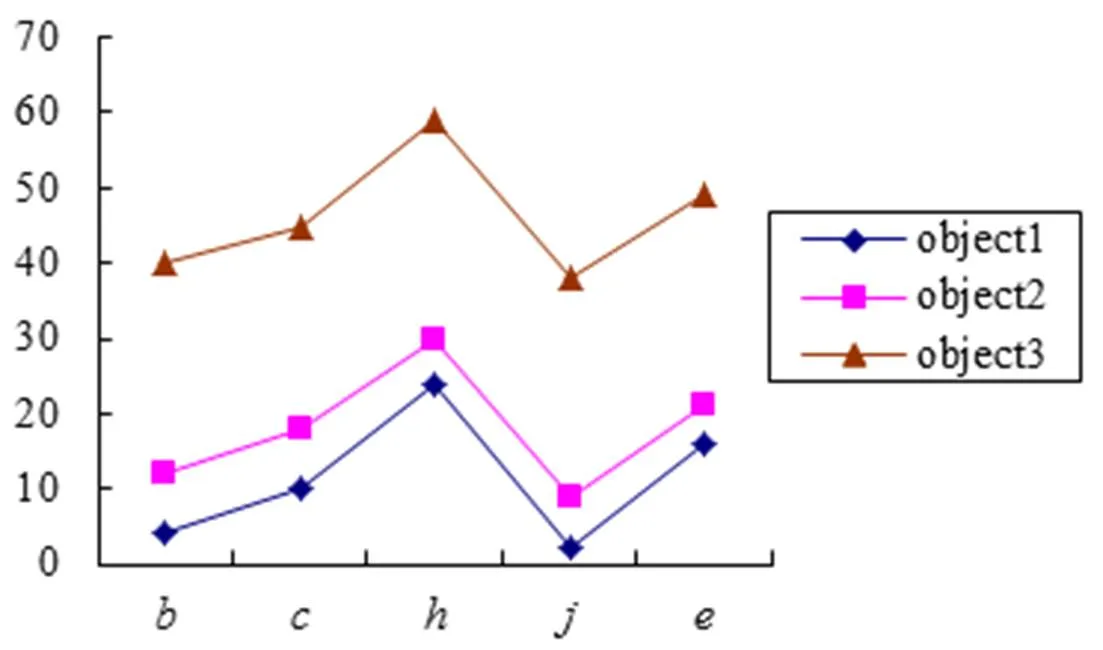
图2　对象的属性子集相似模式

Cheng Y.等在2000年提出了bicluster算法[16]。设为对象的集合，为属性的集合，令⊂且⊂，则（，）表示一个子矩阵，残差的平方的平均值

当(,)≤（>0）时，称为一个-bicluster。

Yang Jiong等提出的基于移动的算法[17]能更快地找到-bicluster。首先随机选择一个起点，迭代地执行算法以改善聚类分群的质量。该算法能够同时找到多个分群，且避免了分群间的重叠问题，但它仍然采用平方差作为分群聚类的基础，当数据集中存在噪声点时，聚类效果并不理想，同时该算法要求输入聚类的群数作为输入参数。

Wang Haixun等[15]使用pScore代替平均平方差，很好地解决了噪声数据的问题。定义为数据集中的对象子集(⊆)，为属性集的子集(⊆)，(,)对代表一个子矩阵。令,∈，,∈， pScore定义为

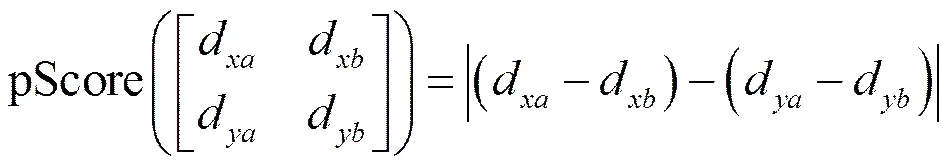
其中d代表对象在属性的取值。

当(,)对中任意2×2子矩阵均满足pScore() ≤时，(,)为一个-pCluster。设=(,)是一个-pCluster，定义是的最大维度集（maximum dimension sets，MDS），当且仅当不存在任意⊃，使得(,)也是一个-pCluster。pCluster算法需对每2个对象及每对属性进行比较，产生MDS。这时将对象对产生的MDS称为o-pair MDS，属性对产生的MDS称为c-pair MDS。由数据集产生的所有MDS中，包含了可能构成pCluster的全部信息。

接下来对o-pair MDS和c-pair MDS进行相互剪枝操作。MDS的剪枝过程是pCluster算法的重要组成部分。假设T是对象和的MDS，O是属性和对应的MDS。对任意一个TMDS中的属性，计算O的MDS中包含{,}的个数，当个数小于-1时（是pCluster要求的最小属性数），则将属性从T中去除，如果剪枝后的|T| <，则移除整个T。该过程即为使用c-pair MDS对o-pair MDS剪枝。反之亦然，只需将替换为（pCluster要求的最小对象数）。反复使用c-pair MDS与o-pair MDS相互剪枝，直至没有任何MDS可被删除为止。

最后将余下的o-pair MDS插入一个以属性为路径的前缀树，相应的对象存放在结点中，再对所有结点，利用对应路径属性对的MDS删除结点中保存的多余对象，并将该结点中对象加入其父节点，删除此结点，重复此过程直到没有深度大于的结点存在。后序遍历该前缀树以得到最终的pCluster结果。

2　改进的pCluster算法

pCluster算法中MDS剪枝操作占用了算法的绝大部分运行开销。当数据集对象或属性数目增加时，MDS剪枝耗时也将随着MDS候选元组数的上升而急剧增加。于是一些文献针对MDS剪枝问题的改进进行了尝试。李健亿等人[18]提出了pCluster的改进算法pCluster+，通过牺牲额外的存储空间对MDS相关信息进行计数，从而提高剪枝效率。pCluster算法的核心是MDS的相互剪枝过程。

本文提出改进的pCluster算法，通过在MDS相互剪枝过程中加入存储检验容器Checkbox，在每次c-pair MDS与o-pair MDS的遍历检查过程中用于存放那些导致被检查的T或O被删除的记录行号。因为Checkbox所存储的行中必然包含被删除记录中的前2个元素，且该记录已被删除，则这2个元素的出现频率也将降低，于是Checkbox所存储的行在下一次剪枝过程中被移除的可能性将大于其它记录，如果对Checkbox中记录的行优先进行检查，就可以避免由于检查记录过多而导致的算法效率缓慢。

假设现有5×5数据集（5个对象，5个属性）如表1所示。

表1　5×5数据集

原始数据中存在5项o-pair MDS，6项c-pair MDS。在本文的改进算法中，加入了一个Checkbox检验存储容器，用于辅助MDS剪枝过程。对于o-pair MDS中(O, O) à {C, C, C}，在c-pair MDS中查找包含(O,O)的项，并将其行号加入preCheckbox中。若最终(O, O) à {C, C, C}由于属性频率或个数未达到阈值被删除，则将preCheckbox中的行号转录至Checkbox，同时清空preCheckbox。在接下来的c-pair MDS遍历中，仅需对Checkbox中记录的c-pair MDS行号进行扫描。同样地，对于记录(C,C) à {O,O,O}，在o-pair MDS中查找包含(C,C)的项，并将其行号加入preCheckbox中。若最终(C,C) à {O,O,O}被删除，则将preCheckbox中行号加入Checkbox，并清空preCheckbox。反复进行这样的操作，直至在完整的一轮检验过程中（o-pair MDS与c-pair MDS相互剪枝）都没有记录被删除。

令= 3，= 3，= 1。首先找到全部MDS，如图3所示。

(1,3)→(1,2,3)

(1,4) →(3,4,5)

(1,5) →(3,4,5)

(2,3)→(1,2,3)

(4,5) →(3,4,5)

(a) o-pair MDS

(1,2) →(1,2,3)

(1,3) →(2,3,4)

(2,3) →(2,3,5)

(3,4) →(1,4,5)

(3,5) →(1,4,O)

(4,5) →(1,4,O)

(b) c-pair MDS

图3数据集中存在的MDS

以上述原始数据举例，先用c-pair MDS对o-pair MDS进行检验，第一项(1,3) à {1,2,3}，在c-pair MDS中包含(1,3)的项中仅在第1行，属性1，2，3出现频率为（1，1，0），于是删除(1,3) à {1,2,3}，并将c-pair MDS行号1加入Checkbox；下一步只检验c-pair MDS的第1行(1,2) à {1,2,3}，包含(1,2)的o-pair MDS仅有(2,3) à {1,2,3}，{1,2,3}频率不满足阈值-1，因此删除该记录，并将o-pair MDS行号3加入Checkbox，至此第一轮剪枝完成。后续剪枝规则相同。当Checkbox为空时，遍历相应MDS中的所有项，否则只需检查Checkbox中记录的行号即可。对于给定的数据集（表1），需进行3轮剪枝过程，如图4所示。

Roud 1: Checkbox = NULL

Part 1:

(1,3) →(1,2,3) ×

(1,4) → (3,4,5)

(1,5) → (3,4,5)

(2,3) → (1,2,3)

(4,5) → (3,4,5)

Checkbox = [1]

Part 2:

(1,2) → (1,23)×

(1,3) → (2,3,4)

(2,3) → (2,3,5)

(3,4) → (1,4,5)

(3,5) → (1,4,5)

(4,5) →(1,4,5)

Checkbox = [3]

Roud 2: Checkbox = [3]

Part 1:

(1,4) →(3,4,5)

(1,5) →(3,4,5)

(2,3) →(1,2,3)×

(4,5) → (3,4,5)

Checkbox = [1, 2]

Part 2:

(1,3) →(2,3,4)×

(2,3) → (2,3,5)×

(3,4) → (1,4,5)

(3,5) → (1,4,5)

(4,5) → (1,4,5)

Checkbox = NULL

Roud 3: Checkbox = NULL

Part 1:

(1,4) →(3,4,5)

(1,5) →(3,4,5)

(4,5) →(3,4,5)

Checkbox = NULL

Part 2:

(3,4) →(1,4,5)

(3,5) →(1,4,5)

(4,5) →(1,4,5)

Checkbox = NULL

图4改进的MDS剪枝过程

比较过程：第一轮，c-pair MDS对o-pair MDS剪枝，Checkbox为空，比较次数5×6，Checkbox=[1]；o-pair MDS只需对c-pair MDS第1行检验是否需要剪枝，比较次数1×4，Checkbox=[3]。第二轮，使用c-pair MDS对o-pair MDS第3行检验，比较次数1×5，Checkbox=[1，2]；o-pair MDS 对c-pair MDS第1行和第2行检验是否需要剪枝，比较次数2×3，Checkbox为空。第三轮，c-pair MDS与o-pair MDS相互检验，比较次数3×3×2，没有记录被删除。MDS剪枝结束。总比较次数为63。原pCluster MDS剪枝过程如下：第一轮c-pair MDS对o-pair MDS剪枝，比较次数为5×6，删除o-pair MDS第一行记录；o-pair MDS对c-pair MDS剪枝，比较次数为6×4，删除c-pair MDS的第1、2、3条记录。第二轮使用c-pair MDS对o-pair MDS进行检验，比较次数为3×4，删除o-pair MDS第三行记录；o-pair MDS对c-pair MDS剪枝，比较次数为3×3，无记录删除。第三轮，c-pair MDS与o-pair MDS相互检验，比较次数3×3×2。总比较次数93。

算法优化了pCluster核心部分，改进了MDS剪枝过程，在保持算法准确性的基础上使算法效率得到显著提高。在改进后的剪枝过程中，利用存储检验容器Checkbox记录下更有可能被剪枝的MDS。使用Checkbox中记录项作为优先检验对象，从而大幅缩小待检查的MDS范围，避免了原算法中每轮剪枝都必须检查全部MDS的繁琐步骤，同时当Checkbox首次为空时，执行一次MDS全面覆盖相互筛查，以保证剪枝结果的正确性，有效避免漏检情况的发生。这样既保证了MDS剪枝的完整性，同时也使算法耗时大幅减少。

改进的pCluster算法：

begin

for each,∈,≠

find c-pair MDSs;

end

for each,∈,≠

find o-pair MDSs;

end

Checkbox = NULL;

do

if Checkbox is empty

for each o-pair MDS

use c-pair MDSs to prune columns in;

if ||<

eliminate MDS({,},);

store sequence number of c-pair MDS in Checkbox;

end

end

if Checkbox is empty

for each c-pair MDS

use o-pair MDSs to prune objects in;

if ||<

eliminate MDS({,},);

store sequence number of c-pair MDS in Checkbox;

end

end

else if Checkbox is not empty

check every c-pair MDS which is recorde-d in Checkbox;

eliminate MDS({,},) and store the sequence number in Checkbox, if ||<;

end

else if Checkbox is not empty

check every o-pair MDS which is recorded in Checkbox;

eliminate MDS({,},) and store the sequence number in Checkbox, which ||<;

end

if no pruning takes place

mutual prune both o-pair MDSs and c-pair MDSs;

end

while pruning takes place

insert all o-pair MDSs({,},) into the prefix tree;

make a post-order traversal of the tree;

do

:= objects in node;

:= columns represented by node;

for each,∈

find c-pair MDSs;

remove fromthose objects not contained in any MDS

end

while no node whose depth > nc exists

end

3　仿真实验与结果分析

对改进的pCluster及原算法进行仿真实验，并对算法效率进行分析与比较。实验平台为处理器Intel(R) core(TM)2 Duo CPU 2.26 GHz，3 G内存，Vista操作系统。实验分别采用人工数据集、经典数据集以及实际采集的医疗数据作为测试数据，不同数据集仿真实验结果均表明改进的pCluster算法较原算法在聚类效率上有显著的提高。

3.1人工数据集

测试数据采用人工数据集，矩阵元素为随机生成的1～100数字。属性个数固定为30，对象个数分别设为10、20、30、50、100。此外，pCluster中最小对象数设为3，最小属性数设为2，阈值为3。原算法与改进算法的运行时间比较如表2所示。第1行表示数据集大小，即对象数×属性数。从表2可以看出，数据集规模较小时，例如10×15，改进算法与原算法耗时几乎相同，随着数据集规模的增大，改进的pCluster算法优势逐渐显现，在对象数为20、30、50的数据集中，改进算法耗时较原算法减少了一个数量级。数据集大小为100×15时，CPU耗时减少了72.94%。

表2　人工数据集仿真结果

3.2酵母菌基因序列数据

测试数据采用经典的数据集酵母菌基因序列片段[19]，数据集中包含2884个基因在17种条件下的记录数据。数据集以矩阵形式显示，每行代表1种基因，每列代表1类环境条件。矩阵中的值由原始数据值采用比例缩放或取对数方式使其数值呈现在0到600之间。生物学家的目标是寻找在相同条件下产生共同趋势的基因组。其中，pCluster最小对象数设为40，最小属性数设为7，阈值为2。2种模式聚类算法对该数据集的测试结果如表3所示。可以看出，原pCluster算法剪枝轮数较少，但耗时集中；改进后的pCluster算法剪枝轮数增加了一倍，但剪枝所需总时间有所减少，较改进前提高了12.04%。

表3　酵母菌基因数据集仿真结果

3.3医疗数据

采用某医院的医疗数据，数据集中包含560名受访者21种症状程度的记录。数据集以矩阵形式存储，每行代表1名受访者，每列代表1类症状。其中，为数据集样本数。pCluster最小属性数设为13，最小对象数设为0.1，阈值为1。2种模式聚类算法对该数据集的测试结果如表4所示。第1行表示数据集大小，即对象数×属性数。实验结果表明，改进的pCluster算法较原算法在效率上有明显的提升。样本数超过200时，改进算法的CPU耗时提高了两个数量级。医疗数据改进的pCluster与原pCluster算法效率比较如图5所示。

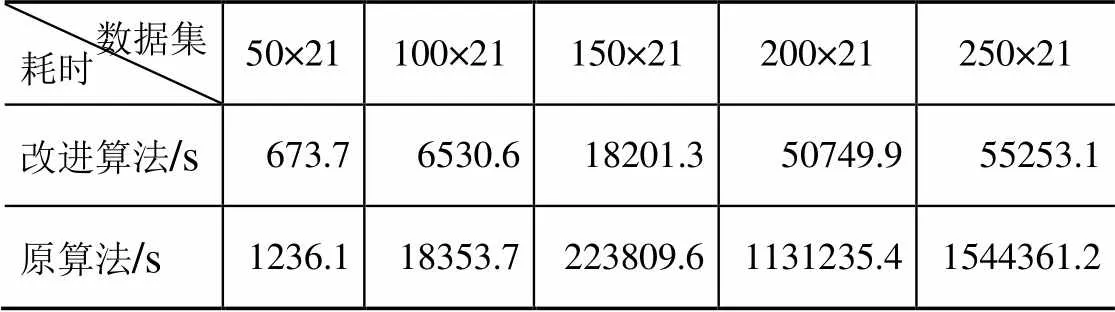
表4　医疗数据集仿真结果

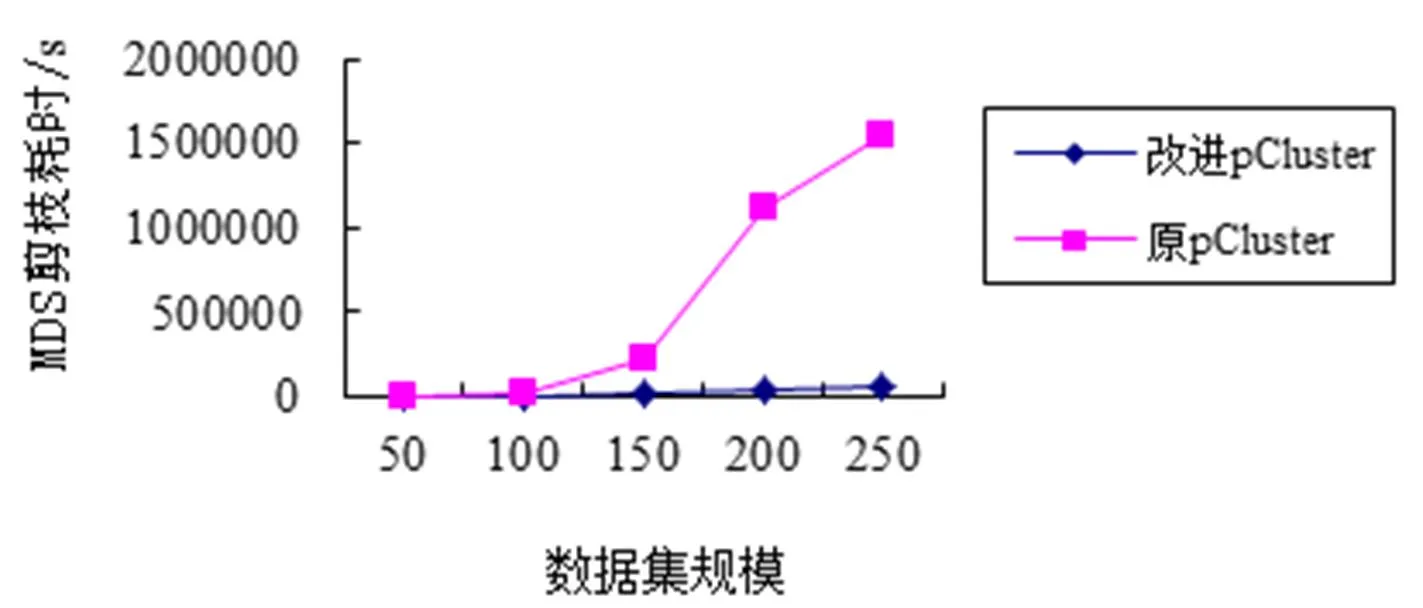
图5 医疗数据改进的pCluster与原pCluster算法效率比较

4　结语

本文提出一种pCluster改进算法，优化了pCluster算法的核心部分—MDS剪枝过程，使发现对象和属性间的相似模式更具效率。改进算法分别在人工数据集和2组真实数据集上进行了仿真实验，测试结果均表明改进的pCluster算法较原算法耗时更少，聚类效率更高。同时，相似模式聚类算法具有广泛的实际应用价值，例如医疗数据分析、商业信息推广、化学结构评价等等，这也是笔者未来工作的方向。

参考文献

[1] Srikant R, Agrawal R. Mining quantitative association rules in large relational tables[C]. Montreal: in Proc. of the ACM SIGMOD International Conference on Management of Data, 1996, 25: 1-12.

[2] Agrawal R, Imielinski T, Swami A. Mining association rules between sets of items in large databases[C]. Washington: in Proc. of the ACM SIGMOD International Conference on Management of Data, 1993, 22:207-216.

[3] 李国雁,沈炯夏.一种基于矩阵的多值关联规则的挖掘算法[J].计算机工程与科学,2008,30(5):72-74,77.

[4] 贺志,田盛丰,黄厚宽.一种挖掘数值属性的二维优化关联规则方法[J].软件学报,2007,18(10):2528-2537.

[5] 陈文.基于位矩阵的加权频繁项集生成算法[J].计算机工程,2010,36(5):54-56.

[6] 姜丽莉,孟凡荣,周勇.多值属性关联规则挖掘的Q-Apriori算法[J].计算机工程,2011,37(9):81-83.

[7] Donoho David L. High-dimentional data analysis: The curses and blessings of dimensionality [R]. Los Angeles, 2000.

[8] Beyer K, Goldstein J, Ramakrishnan R, et al. When is nearest neighbors meaningful[C]. Jerusalem: in Proc. of the International Conference Database Theories, 1999: 217-235.

[9] Agrawal R, Gehrke J, Gunopulos D, et al. Authomatic subspace clustering of high dimensional data for data mining applications[C]. New York: Proc of ACM SIGMOD International Conference on Management of Data, 1998, 27: 94-105.

[10] Aggarwal C C, Yu P S. Finding generalized projected clusters in high dimensional spaces[C]. Dallas: Proc of ACM SIGMOD International Conference on Management of Data, 2000, 29: 70-81.

[11] 宗瑜,李明楚,徐贯东,等.局部显著单元高维聚类算法[J].电子与信息学报,2010,32(11):2107-2712.

[12] Liu Qingbao, Dong Guozhu. CPCQ: Contrast pattern based clustering quality index for categorical data[J]. Pattern Recognition, 2012 ,45 (4): 1739-1748.

[13] Poon Leonard K M, Zhang Nevin L, Liu Tengfei, et al. Model-based clustering of high-dimensional data: Variable selection versus facet determination[OL]. http://www. sciencedirect.com/science/article/pii/S0888613X12001429. 2012.8.

[14] Browne R P, McNicholas P D. Model-based clustering, classification, and discriminant analysis of data with mixed type[J]. Journal of Statistical Planning and Inference, 2012, 142 (11): 2976-2984.

[15] Wang Haixun, Wang Wei, Yang Jiong, et al. Clustering by pattern similarity in large data sets[C]. Madison: in Proc. Of ACM SIGMOD International Conference on Management of Data, 2002:394-405.

[16] Cheng Y, Church G. Biclustering of expression data[C]. San Diego: In Proc. Of 8th International Conference on Intelligent System of Molecular Biology, 2000:93-103.

[17] Yang Jiong, Wang Wei, Wang Haixun, et al. δ-clusters: Capturing subspace correlation in a large data set[C]. San Jose: ICDE, 2002: 517-528.

[18] 李健亿,黃乙展,吴峥榕.新的pCluster方法：pCluster+与incremental pCluster[C].台中:National Computer Symposium ,2003:1114-1121.

[19] Tavazoie S, Hughes J, Campbell M, et al. Yeast micro data set[OL]. http://arep.med.harvard.edu/biclustering/yeast.matrix, 2012.5.

An Improved Pattern Cluster Algorithm for Quantitative Attributes

Wang Shanshan1Liang Tongle2

(1.Department of Computer Engineering, Guangdong Industry Technical College 2. Department of Computer, Guangdong Vocational Technical College of Posts and Telecom)

pCluster is a kind of cluster algorithm for the numeric attributes, which could identify the similar trend among several attributes, but it is less than satisfactory in algorithm efficiency. In this paper, an improved pCluster algorithm was presented, the expected cluster results could be produced more efficient.

Association Rule; Quantitative Attribute; Pattern Cluster

王珊珊，女，1984年生，硕士，助教，主要研究方向：数据挖掘。E-mail: 2014106061@gditc.edu.cn

梁同乐，男，1984年生，学士，助教，主要研究方向：智能信息处理、大数据分析等。