投资者情绪对证券价格波动的影响
——建模与模拟分析
邹辉文,孙 磊,陈圳斌,李永利(福州大学 投资与风险管理研究所,经济与管理学院 福州 350116)
金融市场研究
投资者情绪对证券价格波动的影响
——建模与模拟分析
邹辉文,孙 磊,陈圳斌,李永利
(福州大学 投资与风险管理研究所,经济与管理学院 福州 350116)
证券价格的变动受证券内在价值、投资者情绪及其他因素的影响,通过建模与模拟分析表明,其中投资者情绪对证券价格波动的影响很大。消极情绪、积极情绪与中间情绪对证券价格、投资者财富的影响明显不同,证券价格的变化与投资者情绪变化是一一对应的,但投资者财富的变化与情绪变化不一一对应。当市场整体情绪乐观时,多数人都不愿主动努力寻找私人信息,不愿去认真分析证券的内在价值,而只跟着自己的情绪走,投资者追涨行为加剧,价格被逐渐推高,市场对证券的需求便会出现泡沫;当证券市场处于整体悲观情绪时,则会有相反的结果。
证券价格波动;证券内在价值;投资者情绪;价值预期;行为金融
本文应用建模与模拟分析方法探讨投资者情绪对证券价格波动的影响。建立了证券价格为证券内在价值、投资者情绪和投资者对证券内在价值的预期的线性函数模型,并在一定的条件下求得相应的解释。在此基础上,分析了投资者情绪对证券价格波动的作用和影响。并进一步用市场上投资者对风险证券和无风险证券的投资比例的大小来区别市场上的积极或消极情绪,通过模拟分析说明在证券市场中,消极情绪、积极情绪与中间情绪对证券价格、投资者财富的不同影响。
一、文献综述
20世纪末迅速兴起的行为金融学以其逼近真实市场行为的理论分析显示出广阔的发展前景。行为金融学修正了现代金融理论中理性人假设的论点,指出由于认知过程的偏差和情绪、偏好等心理方面的原因使投资者无法以理性人的方式对证券价格做出无偏差估计。这一发现引起学者对投资者心理研究的普遍关注。就微观而言,分析投资者心理不仅可使自身有效地避免决策错误,还可以基于他人的心理偏差制定特定的投资策略进行套利;就宏观而言,它涉及到证券市场是否有效及证券价格是否反映内在价值等重大问题。因此,探讨投资者情绪对证券价格波动的影响机制具有重要的现实意义。下面对国内外关于投资者情绪的研究做一归纳。
(一)通过理论或实证探讨投资者情绪对投资决策行为和证券价格波动的影响
在国外,Gleicher和Baker(1991)在研究中发现,不好的情绪会使投资者对已有的即使确定的信息做非常仔细的分析和无比精细的挑剔。消极投资者对目前经济形势和判断更谨慎,会详细谨慎分析投资决策过程,通常会做出较为悲观的决定;乐观投资者很少认真分析投资策略,多用启发式策略,通常采用的策略更倾向于乐观自信,投资意愿相应增加[1]。Hirshleifer等(2003)认为:情绪和感情变化会影响投资者对风险忍受的程度,悲观情绪可以使投资者“损失趋避”的程度增加。[2]Kumer(2006)的研究表明个人投资者股票买卖存在一定的同步性;另外,与噪声交易者模型一致,研究结果支持投资者情绪影响收益形成。[3]Schmeling(2009)联合分析了个人投资者与机构投资者对于证券价格的影响。研究发现,情绪会影响股票市场,存在中期(半年)影响,两类投资者存在显著差异。平均来说,机构投资者能正确预测股票市场收益,个人投资者反向预测了市场趋势,个人投资者情绪是噪声交易者风险的代理变量,而机构投资者是经验丰富、消息灵通的精明投资者。[4]
从国内研究方面来看,对投资者情绪的研究起步稍晚,李心丹等(2002)研究了投资者情绪作用于股市的一些证据。[5]刘煜辉等(2003)讨论了资本市场上的各种异常现象的解释,进而运用行为金融理论论证国内资本市场上投资者心理和多变复杂的情绪等行为的影响作用。[6]陈彦斌(2005)研究了情绪波动对股票价格和债券价格波动率的影响,结果表明,投资者的情绪波动对股票价格波动的影响要远大于对债券价格波动的影响;影响股票价格波动的情绪波动分别是主观贴现因子、跨期替代弹性和风险规避系数的波动。[7]朱伟骅和张宗新(2008)的研究表明我国投资者情绪容易受到噪声交易者影响,其他类型交易者可利用噪声交易者的交易策略在博弈中获取超额利润,这为投机性泡沫的产生提供了微观基础。在市场波动机制中,投资者情绪与股价变化存在动态关系,股价泡沫存在内在持续性,引发市场正反馈效应,从而促成投机性泡沫的生成。[8]杨阳和万迪昉(2010)基于上证股市的相关数据,分析不同市场态势下投资者情绪与股市收益及其波动的异化现象。结果表明:我国投资者情绪对股票市场的收益并无显著影响;而股票收益却对投资者情绪的作用显著,牛市阶段股票收益与投资者情绪正相关,而熊市阶段则为负相关。[9]
(二)通过情绪指数探讨投资者情绪与证券价格波动之间的联系
在国外,Brown(1999)利用美国“个人投资者协会”(AAII)提供的投资者情绪指数,通过实证说明了投资者情绪与封闭式基金的价格波动密切相关。[10]Lee et al.(2002)发现投资者的情绪变量是影响股价的系统性因子,超额收益与情绪变化有同期相关关系,投资者情绪变化可以很大地影响收益的波动。[11]Brown与Cliff(2004)认为情绪的水平值大小及变化量与市场收益强相关。[12]Brown和Cliff(2005)探讨了投资者情绪对市场的长期效应,用投资者智能指数作为代理情绪的变量,发现情绪对于股票的长期收益具有预测力,通过构造一个资产定价模型说明定价错误与投资者情绪正相关,而且未来1~3年的收益与情绪负相关。[13]Baker和Wurgle(2006)构建了复合情绪指数,发现情绪对主观估值程度高和难以套利的股票,即小市值股票、发行时间较短的股票、高波动率的股票、非盈利股票、不分红股票、极端成长型股票的影响更大。[14]
从国内研究方面来看,王美今、孙建军(2004)的研究表明,投资者接受价格信号时表现出来的情绪是影响均衡价格的系统性因子,从而构造了新型的投资者情绪指数,构建了TGARCH-M(1,1)模型,实证说明了投资者情绪的变化不仅会显著地对深沪两市收益波动产生影响,且显著地反向修正深沪两市收益波动,并通过“风险奖励”影响收益。[15]张强、杨淑娥(2009)选择市场换手率、封闭式墓金折价和投资者开户增长率作为间接投资者情绪指数,应用因子分析法构造综合投资者情绪指数,并应用OLS和GARCH-M回归分析方法对中国股市投资者情绪及波动与股票收益间的关系进行实证分析。结果显示,投资者情绪是影响股票价格的系统因子,股票价格随着投资者情绪波动而波动,而且情绪的上涨和下降对股票价格的影响是不对称的,情绪上涨对股票价格的影响要比下降强得多。[16]刘莉亚、丁剑平等(2010)通过构建一个新的投资者情绪指标,采用非参数统计和回归模型实证检验了情绪指标的变动对特征组合收益率的影响并给出解释,并通过考虑系统风险的情绪变化与其他情绪代理变量验证了实证结果的稳健性。[17]
(三)通过建模探讨投资者情绪对证券价格波动的影响
在国外,对投资者情绪进行模型分析研究的代表性学者De Long et al(1990)建立了经典的DSSW模型,该模型表明,从理论上讲,如果套利者不能够消除投资者情绪影响所导致的非理性定价,那么投资者的情绪会成为影响资产定价的系统性风险。[18]Barberis et al(1998)提出的BSV模型,描述了投资者情绪如何形成,如何影响证券的均衡价格。[19]Daniel et al(1998)提出DHS模型,把投资者信心分为变量和常量,分别研究了如何影响资产价格的形成过程。[20]Levy et al(1995)建立了一个股市微观模型(即LLS模型),研究股市中出现的周期性的股价涨跌波动现象以及市场中不同类型的有限理性投资者之间的相互作用关系。其建模基础是一般性的证券市场交易程序,而行为金融理论贯穿始终。[21]Barberis et al(2005)应用收益协同运动模型,发现情绪与收益的关联度是投资者“聚集”的函数,即个人投资者持股集中程度越高的股票,其收益与情绪的关联度越高。[22]
从国内研究方面来看,姜继娇等(2006)基于Multi-Agent构建了多心理账户情景下,机构投资者的两级行为投资组合模型,研究结果表明,相对于传统的行为证券组合理论,该模型更为接近证券组合决策的实际情形。[23]李潇潇等(2008)沿用DHS模型研究框架建立了基于投资者情绪的资产定价模型,分析了投资者情绪对资产定价的影响,并利用该模型解释证券市场中的过度反应和过度波动等异常现象;论证了投资者情绪对长期市场收益具有反向影响,并且情绪交易者的存在导致短期资产价格波动变大。[24]唐静武和王聪(2009)在投资者异质性条件下建立了市场情绪与情绪溢价的理论模型,并构建一个衡量市场情绪的综合指标,研究结果表明:中国股市市场情绪产生溢价并使深沪两市的收益产生波动;中国股市不仅有情绪的短期持续性和长期的逆转性,而且存在短期收益惯性和长期收益反转效应;市场情绪是导致中国股市非理性大起大落的重要因素。[25]
由上述可知,目前的研究主要集中于通过经验数据来实证分析情绪与股票收益及其波动性的相关性,同时也有少量的研究从理论和模型的角度探讨投资者情绪对投资决策行为和证券价格波动的影响。但对投资者情绪的形成与时变过程、投资者情绪对证券价格的影响机理等方面还有待深入研究。本文试图从模型和模拟的角度系统探讨投资者情绪的形成与时变过程,并通过对证券内在价值的预期来讨论投资者情绪对证券价格产生影响的机理。
二、投资者情绪对证券价格波动影响的建模与分析
Lux(1995)用系统论的方法严格阐明了投资者情绪在影响证券价格方面起到很大的作用。[26]当市场处于恐慌、悲观的状态下,人们的悲观情绪就像传染病一样开始蔓延。一旦投资者情绪受到重创,投资者对未来预期悲观,政府出台的大量救市措施、数目庞大的注资都不可能在短期内改变这种情绪。政府不可能直接控制投资者的情绪和情绪的变化,此时所谓的内在价值、内幕信息对于处在悲观情绪下的投资者来说统统被抛在脑后,以至对信息反应不足。相反,当市场处于乐观情绪状态时,投资者往往盲目乐观、自信,对金融资产的需求强烈。只要悲观者占上风,资产价格必然下降,反之则上涨。所以,投资者情绪的不稳定必然引起资产价格的异常波动。
由此可见,面对变幻无穷的证券市场,投资者的心理行为并不一定是完全理性的,而是呈现出有限理性的特征。他们在信息获取、加工和输出处理过程都有可能产生心理偏差,进而导致一些投资决策的非理性行为,如从众行为、对股市政策的过度反应,以及操纵证券价格行为等。由于这种对理性决策的偏离往往是系统性的,且这种偏离不能为统计平均而抵消掉,于是常常造成证券价格的异常波动,产生非理性泡沫,对证券市场本身的发展和投资者的合法权益都造成损害。我们下面将这些结论模型化。
(一)模型背景及假设
我们把投资者分为两个群体:乐观情绪的投资者和悲观情绪的投资者,他们的数量分别记为m和n,所以市场上共有m+n个投资者;记乐观情绪投资者所占比例为记悲观情绪投资者所占的比例为乐观情绪投资者群体的整体情绪变量记为ξm,悲观情绪投资者群体的整体情绪变量记为ξn,假如我们以0作为分界线,则可认为ξm>0,ξn<0,于是市场上投资者整体的情绪可以刻画为ψ=κmξm+κnξn。
假设证券市场上只存在两种证券:一种是无风险证券,其无风险收益率记为r0,另外一种证券是风险证券,其收益记为χ,假设χ服从正态分布χ~N(μχ,σχ)。为简化分析而不影响对问题的讨论,我们在此只考虑时间跨度及投资期限为两期情况下的模型。设投资者具有负指数形式的效用函数Ui(w)= -e-λw,其中λ为风险厌恶系数,且λ>0,w为投资者的财富。第t期,第i个投资者的初始禀赋为ai0货币单位的无风险证券,乐观情绪投资者群体和悲观情绪投资者群体对风险证券的需求分别为θm、θn,风险证券的价格为p,所以wt=ai0+θip,i=m,n。在下一期t+ 1时刻,情绪投资者在对风险证券内在价值的预期之下的财富为wt+1=ai0(1+r0)+θi(χ+ξi),i=m,n。易知:wt+1=wt(1+r0)+θi[χ+ξi-p(1+r0)],i=m,n。
市场上的投资者由于对未来不确定性的预期不同,如对公布的宏观经济的景气数据、相关行业前景、公司的盈利状况、公司现金流等各项财务指标预期的不同,从而造成投资者对所持有证券的公司内在价值的预期有很大的差别,投资者的理性行为体现在对预期不同的条件差异下最大化各自的期望效用函数。也就是说,投资者对所持有证券的公司内在价值的预期是由心理因素决定的,它独立于证券的公司内在价值。这样一来,不同情绪投资者造成了对风险证券的不同需求。对未来不同的预期使投资者出现不同程度的悲观或乐观情绪,为此,假设乐观情绪的投资者对证券内在价值的预期信息为φm=χ+ εm,εm~N(0,σm),同样悲观情绪投资者对证券内在价值的预期信息为φn=χ-εn,εn~N(0,σn)。
(二)投资者情绪对证券价格波动影响的建模
王一鸣(2000)指出,理性预期均衡具有两个性质:一个是均衡价格传递的信息包含任何私人信息,如果是这样的话,那么在均衡价格下,任何私人信息都是多余的;另一个是理性预期均衡与所有投资者收到信息的经济竞争均衡一致。这样的均衡就是完全揭示的理性预期均衡,市场是强有效的。[27]然而,有多种证据证实证券市场并不是强有效的,在完全揭示的理性预期价格系统下,信息的搜集变得毫无价值,所以它是自相矛盾的。在半强效市场上或弱势市场上,价格系统是部分揭示的,投资者对风险证券的需求不仅依赖价格信息,而且还依赖自己的私人信息、个人对证券内在价值的预期判断,以及证券市场上整体情绪等因素的影响。只有在部分揭示的价格系统中才更符合证券市场的现实价格走势,更符合投资者的实际心理感受。
为了更加真实地反应实际证券市场上的部分价格揭示的系统,我们假设证券价格是证券内在价值、投资者情绪和投资者对证券内在价值预期的函数,此假设在一定的情况下是符合投资者决策行为的,投资者在有限理性下,认为自己是按照一定的判断和推理,经过与众不同的分析后对证券内在价值的判断做出投资行为。在这样的背景假设下证券的价格均衡系统是更符合现实的部分揭示价格系统,为此记证券价格为证券内在价值、投资者情绪和投资者对证券内在价值的预期的线性形式为:

其中v是证券内在价值,ψ是投资者情绪,φ是投资者对证券内在价值的预期;由前面所述,它们是互不相关的变量。β>0,γ>0,δ>0是未知参数。
上式意味着证券价格是证券内在价值、投资者情绪变量和投资者对证券内在价值的预期的增函数,证券内在价值的增加自然会导致证券价格的增加;如果市场上投资者预期证券内在价值会增加,同样会导致证券价格的上升;如果市场上是乐观情绪占优,则会使证券的需求增加,便会抬高证券的价格,当市场处于悲观情绪时,情绪的传染会使市场悲观情绪更加迅速膨胀,证券价格会降低。
下面以乐观情绪投资者为例进行模型求解。
乐观情绪投资者在预期到证券内在价值的条件下最大化自己的期望效用,即相当于最大化E[U(wt+1|φm)](这里E[U(·|φm)]表示求条件数学期望,下同),又易知wt+1服从正态分布N(μ,σ2),所以有:

所以乐观情绪投资者会选择适合自己的风险证券的需求数量来使自己的期望效用式(1)最大化,对于求最优的需求数量θm来说,它与下式等价:

对上式求极值可得如下关于投资者内在价值和投资者情绪的风险证券一般需求表达式:

同样对于悲观情绪投资者而言,可求得对于风险证券一般需求表达式:

由投资者的需求表达式可知,投资者关于风险证券的厌恶系数λ对于证券的需求有较大的影响。当投资者越是厌恶风险证券,对投资风险证券越谨慎时,λ变得越大,而θm或θn会变得越小,投资者对于证券需求减少。
假设μχ=v,由数理统计知识,易得(因为篇幅所限本文略去相关公式推导过程,只给出所得结果):

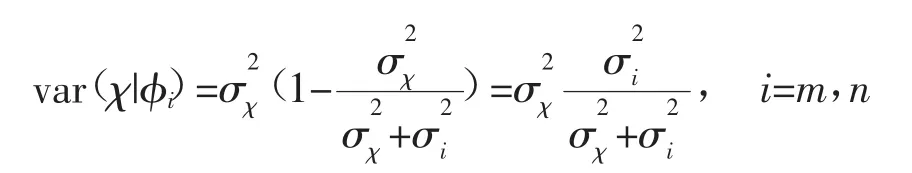
由市场出清条件κmθm+κnθn=1及E(χ|φi)、var(χ| φi)(其中i=m,n)的表达式,联立式(2)和(3),可得到下式:

为简化计算,假设σm=σn=σ0,此假设意味着悲观情绪投资者和乐观情绪投资者对证券内在价值的预期偏差幅度是相同的,只是方向不同。与现实市场情况相比,此假设可认为是近似合理的。把σm=σn= σ0代入式(4)继续化简如下:
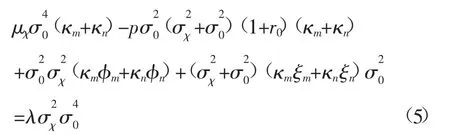
证券市场上关于风险证券内在价值的预期可以看作是悲观情绪和乐观情绪投资者对证券内在价值预期的加权均值,即:

证券市场上整体的投资者情绪也可以看作是市场情绪的加权均值,即:

且由已知条件知:

把式(6)、(7)和(8)代入式(5),并在方程两边消去σ20可得:
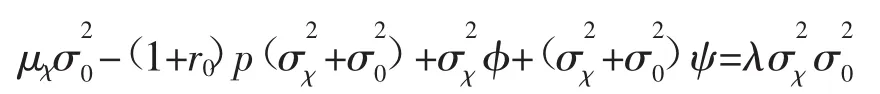
假设μχ=v,从上式里解出风险证券的均衡价格函数p(v,ψ,φ)的表达式为:
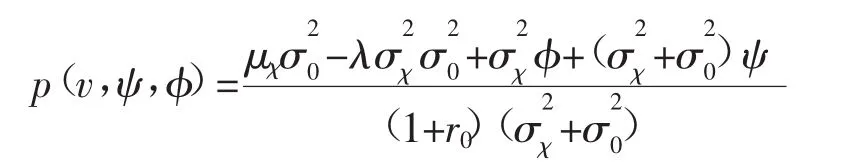
即p(v,ψ,φ)又可表示为:
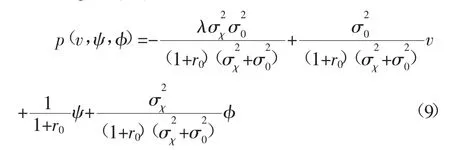
其中参数:

由截距项的表达式可知α<0,α与证券收益的波动水平σχ、投资者的风险厌恶系数λ、无风险收益率r0有关,并且随投资者对证券内在价值预期信息的标准差变化而变化。当λ、σχ和r0在某时刻t为常数时,此截距项表示投资者从均衡价格中推断私人信息对于证券内在价值的误差程度。其余参数β、γ、δ均大于0,说明证券价格与其内在价值、投资者情绪以及投资者的预期信息成正比。
式(9)便是在关于证券内在价值和投资者情绪的统一框架下,金融市场上证券价格的决定方程。由此价格决定方程可知,由于资本市场上投资者情绪的作用以及情绪的不确定性,证券价格的决定是部分揭示的,更符合我们前文所做的分析。部分揭示的价格系统也更能真实反应证券市场价格的不确定性,投资者依据自身的私人信息判断市场上整体所处的状态,才能更好地做出预测。
(三)投资者情绪对证券价格波动影响的模型分析
1.当σ20=0时
σ20=0,说明悲观和乐观投资者对证券内在价值信息的判断从整体上来看是准确的。即φi=χ,i=m,n,投资者根据个人的信息可以确切知道证券内在价值的真实信息,证券内在价值的变化早就反映在投资者对证券内在价值的预期中,于是,证券内在价值并不直接作用于证券价格(因这时β=0),但会通过投资者对证券内在价值的预期作用于证券价格。事实上,这时,投资者对证券内在价值的预期φ=κmφm+ κnφn=χ,而E[φ]=E[χ]=μχ=v。
由式(9)可得:

所以这时证券价格完全由投资者对证券内在价值的预期和投资者整体情绪共同决定。
在短期内,证券内在价值的变化一般比较平稳,E[φ]=E[χ]=μχ=v,且σ20=0,从而投资者对证券内在价值的预期变化也较平稳,而证券价格的异常波动往往是由于投资者的情绪冲动造成的。在短期内,证券市场上投资者的情绪较易受到各种传言和对公司未来发展的预期和当前经济形势的影响,悲观和乐观的情绪很快蔓延,从而造成对证券的需求变动较大,直接导致证券价格的异常波动。
2.当σ20≠0时
在现实中由于投资者私人信息的获得渠道,信息获得成本及对证券内在价值、公司未来发展前景的预期等方面存在偏差,σ20=0一般不成立。由p的表达式可知,只要σ20≠0,证券价格既取决于证券内在价值的影响,还会受到投资者对证券内在价值的预期偏差和投资者整体情绪的影响,所以证券价格就不能充分反应证券内在价值。
由式(10)可知,当σ20<σ2χ时,β<δ;当σ20>σ2χ时,β>δ。这说明当投资者对证券内在价值的预期波动率比证券内在价值的波动率小时,证券内在价值的影响较小;当投资者对证券内在价值的预期波动率比证券内在价值的波动率大时,证券内在价值的影响较大。这与σ20=0时的分析是相一致的。又由式(10)可知:β<γ,δ<γ,从而故投资者整体情绪ψ对证券价格p的影响最大。
当市场整体情绪是乐观时,此时ψ>0,证券价格就在证券内在价值的基础上再被投资者乐观情绪所不断推高。由乐观投资者需求关系式θm=且由假设乐观投资者情绪变量ξm>0,可知此时投资者对证券的需求会高于不考虑投资者情绪时对证券的需求。另一方面,由于投资者情绪对于证券价格的影响大于证券内在价值对于证券价格的影响,这反应了市场整体的一种看法和趋势,多数投资者的行为影响着证券价格,他们把证券内在价值的信息影响抛在一边,忽视影响证券价格的本质是证券内在价值这一主要因素,于是多数人都不愿主动努力寻找私人信息,不愿去认真分析证券的内在价值,而只跟着自己的情绪走。投资者被乐观的预期冲昏了头,受到非理性现象影响追涨行为加剧,并且乐观情绪相互传染,市场对于证券的需求便会出现泡沫,价格被逐渐推高,出现非理性繁荣。
同理,当证券市场处于整体悲观情绪时,投资者杀跌行为加剧,也可做相似分析。
三、投资者情绪对证券价格波动影响的模拟分析
(一)模拟模型的构造
LLS模型假设投资者对未来证券收益率R的数学期望是在过去收益率基础上的一个叠代。即每个投资者通过分析过去k次交易此证券的收益,然后按自己的投资理念对这k个收益进行“叠代”,得出未来值R的数学期望,而不同的投资者叠代区间不同。然后投资者再根据自己的财富分布w(个人财富中持有风险证券的部分)和最近k次交易证券收益情况来进行下一次叠代,不断重复此过程,就形成了一个动态的证券市场价格。[28]
1.同质的证券市场投资者模型
投资者从他们的财富中得到“满足”或“效用”。每一个投资者都有一个财富w的效用函数U(w),反映了他的个人偏好。这个效用是财富w的严格单调递增函数,也是严格凹函数(一阶导大于零,二阶导小于零)。在同质模型中,假设所有的投资者都有相同的效用函数。在不确定的情形下,每一个投资者的目的就是将他们的财富分配于两种证券中,最大化他的期望效用。
风险证券收益由两部分组成:资本利得(损失)Pt-Pt-1和红利Dt,这里Pt为时刻t的证券价格。这样,证券在t时间段的总收益率Pt可以用下式来表示:

为了在风险证券与无风险证券之间做出最优的投资组合,投资者需要考虑的是事前收益。然而,由于实际上这些收益基本上得不到,模型中假设用事后收益的分布作为事前收益分布的估计。
在该模型中,投资者跟踪记忆证券的过去k个收益,把它们称作证券的历史。假设投资者都有一个有限的记忆,并且他们相信,过去的k个历史数据Rj(j=t,t-1,…,t-k+1)中每一个都有相同的概率1/k会在下一个时刻t+1出现。
(1)动态过程
设第i个投资者在时刻t的财富用wt(i)表示,并且这个投资者所持有的证券份额数为θt(i)。下面对时刻t+1的情况进行分析。
(2)证券收入增益
在时刻t和时刻t+1之间,投资者得到风险证券的红利θt(i)Dt和无风险证券的利息[wt(i)-θt(i)Pt]r0。这样,在t+1时刻交易前,投资者i的财富为:

在时间[t,t+1]间隔内,证券市场是没有交易的,所以,证券价格并不会改变,也就没有资本收益或损失。然而,在下一次交易时刻t+1,资本收益或损失就会发生。
证券的需求函数与均衡价格。该模型从假设的价格Ph出发得到总体的需求函数,然后基于此和市场均衡得出均衡价格,并把它作为时刻t+1的证券价格:。
假设在时刻t+1的交易中,证券价格设定为Ph。这样,交易结束后投资者的财富数量将会改变为θt(i)(Ph-Pt)。注意到,只有在交易前持有的θt(i)数量的证券上会有资本损益的变化,而变化并不会发生于在t+1时刻买或卖的证券上。于是,结合式(12)可知,投资者i在时刻t+1交易后的假设财富wh(i)将是:

投资者必须在t+1时刻决定如何投资他的财富,以最大化他下一时期t+2的期望效用。前面提过,事后收益分布是用事前收益分布的估计来代替的。假设投资者i在时刻t+1投资了财富比例为X(i)在证券上,则他在时刻t+2的期望效用为:

假设最优投资比例为Xh(i),则投资者i基于假设价格Ph上持有的证券财富数量为Xh(i)wh(i)。所以,投资者i基于假设价格Ph下愿意持有的证券数量为:

这构成了投资者i的个人需求曲线。将所有个人需求函数加总,就得到以下总的需求函数:

由于用N表示的证券市场上所有的证券数量是固定的,即证券市场总供给是固定的,那么总的需求函数就决定了均衡价格将于总需求函数和总供给函数的交点给出,而供给函数是一条直线。这样,证券在时刻t+1的均衡价格Pt+1将是P*h。
(3)历史更新
新的证券价格Pt+1和红利Dt+1,由式(11)将共同给出一个新的证券收益Rt+1=(Pt+1-Pt+Dt)/Pt。最后,模型将这个最新的收益更新到证券历史中,并将最老的收益数据Rt-k+1从历史中剔除,到此已经完成了一整个周期。一系列时间上证券市场的演化模拟就是重复这个循环。
2.含噪声的证券市场投资者模型
到现在为止,模型描述都是确定性的,做决策的过程是由最大化期望效用导出。在更现实的情形下,投资者并不仅仅是理性效用最大化的,还要受其他很多因素影响。假设很多并不相关的随机影响的净影响是一个正态分布的随机影响,或者叫做“噪声”。因此,模型通过增加一个正态随机变量到最优化投资组合中来考虑所有未知因素对决策做出的影响。具体地说,模型现在要用X*(i)代替X(i),而

其中ε(i)是从一个具有标准离差为σ的正态分布中随机取出的。应该强调的是,X(i)对所有投资者都是相同的,而X*(i)不是,因为ε(i)是对每一个投资者分别取出的。如此,这个噪声就是针对每个投资者的,也就是引进投资者异质的一个重要因素。
3.含情绪的证券市场投资者模型
原LLS模型并没有直接考虑投资者情绪的作用。本文用市场上投资者对风险证券投资比例的大小来区别市场上的积极或消极情绪。投资比例较大,表示投资者较乐观,市场情绪较积极;投资比例较小,表示投资者较悲观,市场情绪较消极。它们在模型中的表现分别为:
(1)消极市场。投资者对市场持极端消极悲观态度,并且在理性程度上单纯决定不投资风险证券而全部投资无风险证券;实际上每个投资者仍然受随机的非理性因素影响,因此模型中的实际投资比例仍然表现为在原理性策略(消极市场下Xn(i))上加随机噪声εn(i)。
(2)积极市场。投资者对市场持极端积极乐观态度,并且在理性程度上单纯决定全部投资风险证券的市场而不投资无风险证券;实际上每个投资者仍然受随机的非理性因素影响,因此模型中的实际投资比例仍然表现为在原理性策略(积极市场下Xm(i))上加随机噪声εm(i)。
(3)中间市场。投资者无法判断未来市场走势,本模型假设在理性程度上投资者决定拿一半财富投资风险证券而另一半财富投资无风险证券;同样,实际上每个投资者仍然受随机的非理性因素影响,因此模型中的实际投资比例仍然表现为在原理性策略(中间市场下Xb(i))上加随机噪声εb(i)。
以下的模拟过程将在此模型基础上展开。
(二)投资者情绪模型的MATLAB模拟
为了计算简便,下面选择对数效用函数ln(w)进行模拟。对数效用函数与负指数形式的效用函数具有相同的基本性质:是财富w的严格单调递增函数,也是严格凹函数(一阶导大于零,二阶导小于零)。
有关数据选取。在LLS模型所讨论的模拟中,选择每两次交易间隔的时间段为一年。无风险证券收益率设为4%。初始市场历史条件,由收益的一个具体分布组成,均值为4.15%,标准离差为0.3%。这些参数使得对风险证券的第一轮投资组合大约为50%,这样在最初的市场上无风险证券和风险证券是很接近的。设投资者的数目为100,最大证券数为10 000,每个投资者的初始财富为1000美元,初始证券价格为4美元,初始红利设为0.2美元(红利收益为5%)。设红利以每年5%的速度增长。这是与标准普尔指数的长期红利增长率接近的。
以上数据选取具有普遍性,本文仍延用作为基本数据。
1.有噪声市场情形
我们在模拟过程中,为了与实际情形契合加进第一个投资者异质因素——噪声。噪声模拟是通过投资者在完全理性基础上,做出投资风险证券比例之后,在这个比例上加上一组(100个)随机数而实现。其中100个随机数中每一个分别对应100个投资者中的一个投资者。
假设记忆长度为k=15,投资者证券投资比例的选择为理性选择X加一个随机变量,并设每个投资者在理性基础上,有正态分布的非理性因素,标准离差是0.2,对此情形做进一步的模拟。证券投资比例X的选择可以用来代表投资者的风险偏好,当不存在卖空机制时,它越接近于1,表示投资者越倾向于购买风险证券。
投资者在理性假设中做出的投资决策X在[0,1]中取值,如果理性基础是X=1(当投资者都认为风险证券收益率更大),或者X=0(当投资者认为无风险证券收益率更大),那么在加上随机的非理性因素之后,可能会有小于0或大于1的比例值存在,这时把这些都手动改为0或1(若原X小于0则改为0,若原X大于1则改为1)。因为模型假设是没有卖空机制的,由此投资者不能买大于自己财富值的证券,也不能卖出自己并未实际持有的证券。
模拟结果如下:将上述基本数据和加噪声后的数据代入LLS模型进行模拟,得出证券价格在第一次交易后升到9.722美元。每个投资者都有了自己的投资比例X(i);每个投资者手中所拥有的证券数量也不尽相同;但每个投资者现在所拥有的财富仍然是相同的:1040美元(因为只是头一笔交易后才持有证券,所以投资者的财富并没有因为证券价格变动而增值,仍是原来财富1040美元)。
但历史收益数据更新之后,投资者拥有的财富开始发生变化。下一次在投资者有各自不同的投资决策(表现为相同比例X加上随机数之后的投资比例)以及不同现有状态(表现为拥有的财富不同,以及持有股数量不同)的基础上,重新选择投资比例,得到一系列新结果(包括这轮证券价格,之后的财富分布,历史收益数据更新,投资者所持有的股票数量分布);之后循环持续下去。
2.情绪市场情形
我们要探讨的问题是:在长线投资条件下,市场的情绪将怎样影响市场走势。在模拟中,用市场上投资者对风险证券投资比例X的大小来区别市场上的积极或消极情绪。投资比例较大,表示投资者较乐观,市场情绪较积极;投资比例较小,表示投资者较悲观,市场情绪较消极。模型试图探讨的是,对比证券价格将如何变化。模拟结果如下:
从图1的证券价格对比曲线中可以看出,消极情绪市场中或者当所有投资者处于消极悲观情绪中时,证券价格会急速下跌83%(从4美元到0.69美元),之后慢速回升,到大约20个交易时刻才回升到最初水平。
而在积极市场中,证券价格从最初的4美元开始经过每个交易日后呈指数上升,直到大约20个交易时刻之后,已经攀升到接近140美元,几乎成为初始价格的40倍,也相当于接近同期消极市场的40倍。由投资者情绪造成的市场情绪对证券价格的影响力是显而易见的。
中间市场中,从最初的证券价格状态4美元到第20个交易时刻是20.726美元。介于消极市场与积极市场之间。

图1 不同情绪市场证券价格变化曲线
由模拟结果的财富分布曲线(见图2)可知,相对于积极情绪市场而言,在消极情绪与中间情绪市场中,投资者所获得财富数目绝大部分时刻都小于积极情绪市场中投资者所获得的财富。这是因为在积极情绪市场中投资者对证券市场持续乐观,做出买进决策,由供求曲线平衡导致价格上涨,市场中所有证券市值也随着情绪的高昂而持续升值,于是投资者财富市值也相随增长。

图2 不同情绪市场某时刻投资者财富分布图
与此同时,从图2中比较中间情绪市场与消极情绪市场的财富分布曲线可以发现,在消极情绪市场中,财富的分布不像中间情绪市场分布相对均匀,部分投资者财富低于中间情绪市场财富,也有部分投资者所获得财富高于中间情绪市场投资者所获得财富,并且这样的高于中间情绪市场财富现象的出现并非偶然。这说明,在熊市中,投资者在对证券市场悲观的情况下也可能获得比非熊市更多的投资财富增值。模拟数据显示,在积极情绪市场中,某一时刻所有投资者财富为1 776 100,同期悲观情绪市场中为320 010,而同期中间情绪市场中则为717 020。以上结果说明,市场情绪的高涨或低迷会使得证券市场总市值升值或缩水,但并非所有投资者一定会在牛市比在熊市盈利更多,或者亏损更少。
四、结论
通过建模分析,说明当投资者根据个人的信息可以确切知道证券内在价值真实信息时,证券内在价值并不直接作用于证券价格,证券价格完全由投资者对证券内在价值的预期和投资者整体情绪共同决定;这时,在短期内,证券价格的异常波动往往是由于投资者的情绪冲动造成的。当投资者根据个人的信息不能确切知道证券内在价值真实信息时,证券价格既取决于证券内在价值的影响,还会受到投资者对证券内在价值的预期偏差和投资者整体情绪的影响,所以证券价格就不能充分反应证券内在价值,并且投资者整体情绪对证券价格的影响最大。当市场整体情绪是乐观时,多数人都不愿主动努力寻找私人信息,不愿去认真分析证券的内在价值,而只跟着自己的情绪走,投资者追涨行为加剧,证券价格被逐渐推高,市场对于证券的需求便会出现泡沫;当证券市场处于整体悲观情绪时,则会有相反的结果。
通过模拟分析,说明无噪声市场是一个没有交易的市场。噪声交易者市场与理性交易者市场的不同主要表现在:市场开始有交易发生;投资者手中不仅持有风险证券,并且持有风险证券的数量有变化;证券价格开始出现趋于理性攀升的阶段;投资者之间财富分布更具市场性,即并非所有投资者财富分布都相同。在情绪市场中,消极情绪、积极情绪与中间情绪对证券价格、投资者财富的影响明显,证券价格的变化与情绪变化是一一对应的,但投资者财富的变化与情绪变化不是一一对应的;虽然积极情绪市场中投资者所获得的财富最大,但中间情绪市场与消极情绪市场相比投资者所获得财富有高有低。
两种分析方法所得的结论基本上是一致的,即投资者情绪对证券价格波动的影响很大。监管部门在制定相关政策时,应充分考虑到这一点。
[1]Petty,R.E.,F.Gleicher and S.M.Baker.Multiple roles for affect inpersuasion[J].Emotion and Social Judgments,1991(3):181-200.
[2]Hirshleifer,D.and T.Shumway.Good day sunshine:Stock returns and theweather[J].Journal of Finance.2003(3):1009-1032.
[3]Kumar,A.and C.M C.Lee.Retail investor sentiment and return comovements[J].The Journal of Finance,2006,61(5):2451-2486.
[4]Schmeling M.Investor sentiment and stock returns:Some international evidence[J].Journal of Empirical Finance,2009,16(3):394-408.
[5]李心丹,王翼宁,傅浩.中国个体证券投资者交易行为的实证研究[J].经济研究,2002(11):54-63.
[6]刘煜辉,贺菊煌,沈可挺.中国股市中信息反应模式的实证分析[J].管理世界,2003(8):6-15.
[7]陈彦斌.情绪波动和资产价格波动[J].经济研究,2005(3):36-45.
[8]朱伟骅,张宗新.投资者情绪、市场波动与股市泡沫[J].经济理论与经济管理,2008(2):45-50.
[9]杨阳,万迪昉.不同市态下投资者情绪与股市收益、收益波动的异化现象——基于上证股市的实证分析[J].系统工程,2010,28(1):19-23.
[10]Brown,G.Volatility,Sentiment and noise traders[J].Financial Analyst Journal,1999,55(2):82-90.
[11]Lee,W.J.,C.X.Jiang and D.C.Indro.Stock market volatility,excess returns,and the role of investor sentiment[J].Journal of Banking&Finance,2002,26(12):2277-2299.
[12]Brown,G.W.and M.T.Cliff.Investor sentiment and the nearterm stock market[J].Journal of Empirical Finance,2004,11(1):1-27.
[13]Brown,G.W.and M.T.Cliff.Investor sentiment and asset valuation[J].The Journal of Business,2005,78,(2):405-440.
[14]Baker,M.and J.Wurgler.Investor sentiment and the cross section of stock returns[J].Journal of Finance,2006,61(4):1640-1680.
[15]王美今,孙建军.中国股市收益、收益波动与投资者情绪[J].经济研究,2004(10):75-83.
[16]张强,杨淑娥.噪声交易、投资者情绪波动与股票收益[J].系统工程理论与实践,2009,29(3):40-47.
[17]刘莉亚,丁剑平,陈振瑜,相恒宁.投资者情绪对资本市场稳定性的实证研究——来自截面效应的分析[J].财经研究,2010(3):133-143.
[18]De Long,J.B.,A.Shleifer,L.Summers and R.J.Waldmann. Noise trader risk in financialmarkets[J].Journal of Political Economy.1990,98(4):703-738.
[19]Barberis,N.,A.Shleifer and R.Vishny.A model of inverstor sentiment[J].Journal of Finance Economics,1998,49(3):307-403.
[20]Daniel,K.D.,D.Hirshleifer and A.Subrahmanyam.Inverstor psychology and securitymarket and over-reactions[J].Journal of finance,1998,53(6):1839-1885.
[21]Levy,M.,H.Levy,and S.Solomon.Microscopic Simulation of the Stock Market:the Effect of Microscopic Diversity[J].Journal de Physique.IFrance,1995,5(8):1087-1107.
[22]Barbcris,N.,A.Shleifer and J.Wurgler.Comovemcnt[J].Journal of Financial Economics,2005(2):283-317.
[23]姜继娇,杨乃定,王良.基于Multi-Agent的机构投资者行为投资组合模型[J].运筹学学报,2006(9):114-120.
[24]李潇潇,杨春鹏,姜伟.基于投资者情绪的行为资产定价模型[J].青岛大学学报(自然科学版),2008(4):95-98.
[25]唐静武,王聪.市场情绪、溢价与波动[J].经济评论,2009(4):58-64.
[26]Lux,Thomas.Herd behavior,Bubbles and Crashes[J].The Economic Journal,1995,105(431):881-896.
[27]王一鸣.数理金融学[M].北京:北京大学出版社,2000.
[28]李心丹.行为金融学——理论及中国的证据[M].上海:上海三联书店,2004.
(责任编辑;校对:李丹)
F830.91
:A
:1006-3544(2015)06-0043-10
2015-07-27
国家社会科学基金后期资助项目(10FGL003)
邹辉文(1959-),男,江西省崇仁县人,福州大学经济与管理学院教授、博士生导师,投资与风险管理研究所所长,研究方向为金融工程与投资理论。

