流体机械中涡轮受力的数值模拟与分析

陈 聪

涡轮是流体机械中很重要的一类装置，在涡轮中应用计算流体力学软件CFD 对流体机械中涡轮简化模型的受力情况进行数值模拟，当有流体经过涡轮的槽时，动叶会受到流体给的使其闭合的力矩。并且，随着两轮的槽慢慢错位，所受到的力矩会逐渐增大。

概述

涡轮是流体机械中很重要的一种装置，是一种以流体为工作介质来转换能量的装置。燃气轮机、液力耦合器、液力变矩器、气动马达和液压马达等流体机械中都有涡轮装置的应用。

传统的流体机械设计是依据试验数据和经验公式，但是实验数据和经验公式适用极窄，一旦结构形式的改变，试验数据就只能作为参考，不能准确分析新机型的流场。而计算流体力学软件CFD 的出现改变了这个现状，它不但能更加方便的分析已有模型的受力，更能为流体机械地设计提供数值模拟，模拟结果虽然会存在一些误差，但是仍能为涡轮等流体机械装置的设计提供参考。

笔者在本文中使用计算流体力学软件CFD 中的Fluent 软件对涡轮的简化模型进行模拟计算，分析流体经静叶流向动叶时不同开度下动叶所受力矩的情况。

计算流体力学分析步骤

用CFD 进行流体动力学分析，步骤如图1 所示。Gambit 作为Fluent 的专业前处理工具，可以完成模型的创建、网格划分和边界条件的施加等。

物理模型

基本条件

本文模拟中使用的流体为水，因为水的性质较为稳定，设定其为理想流体，水温为20℃，入口速度为2m/s。

几何模型

本文中模拟采用的几何模型如图2。

图中Inlet 设定的是速度入口，速度为2m/s，宽度为5cm；Outlet1、Outlet2、Outlet3 均为压力出口，相对压力为0Pa；Outlet1、Outlet3 宽度均为1cm，Outlet2宽度为5cm；Inlet 与Outlet2 来流长度均为10cm。其他表面均设置为绝热固体墙体。

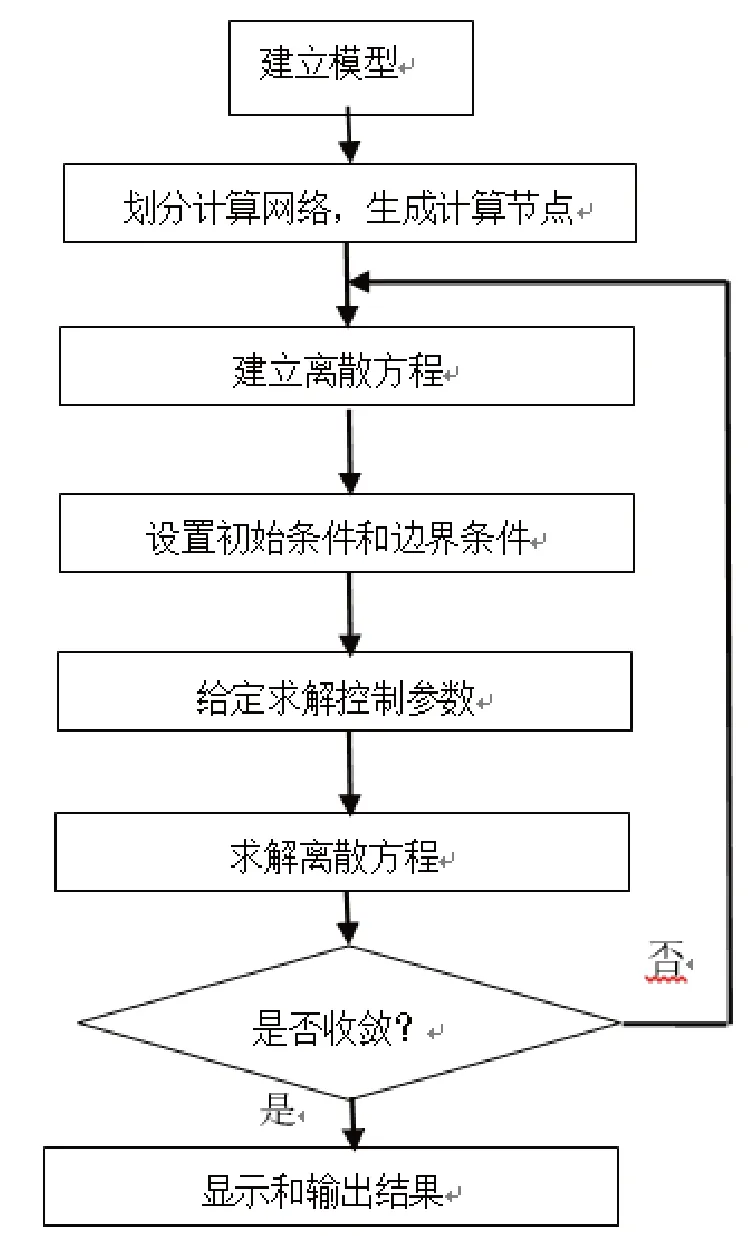
图1 模型分析步骤

图2 几何模型

图3 不同开度下压力与速度分布

表1 K=4/5 时受力面收到Y 方向的力

图4 受力面所受到力的趋势图

定义开度K 为Inlet 与Outlet2 的重合部分与Inlet 宽度的比，如图2 中给的模型开度K=4/5。

数学模型

控制方程

流体的雷诺数为Re=管径D×流速v×流体密度ρ/流体黏度η。本模型中管径D 为5cm，流速v为2m/s，流体密度定为1000kg/m3，流体黏度η 为1×10-3Pa·s，因此可以大概计算出实验中水雷诺数为1×105，这样就可以把流体流态定为湍流，其控制方程满足连续性方程，N-S 方程。

湍流模型

本文选择湍流计算中应用范围最广的k-ε两方程模型。是通过增加单位质量流体湍流脉动动能k 和单位质量流体脉动动能耗散率ε 的控制方程使湍流时均方程组封闭。

计算结果与分析

当流体流过模型的空间时，由于流体的黏性，就会对受力面产生一定的黏滞力，从而对受力面有一定的压力，下面用Fluent 软件模拟分析下受力面所受到的压力方向与大小。

但开度K 不同时，模型的压力、速度如图3。

由图3（a）可以看出压力最大处在模型主入口与主出口相错开的地方，而图3（b）可以看到速度最大处在主入口与主出口相重合的地方，并且，基本速度越大的地方压力越小，这种现象基本符合伯努利方程。

经过Fluent 软件可以计算出受力面所受到的Y 方向的力如表1。

根据四组模拟得出的受力面Y 方向受到的力可以得出：受力面所受到的是向下（-Y）方向的力，并且随着开度的减小，压力系数和总系数都是增大的，也就是受力面受到向下的力逐渐增大，并且基本呈线性变化。趋势如图4。

结语

用计算流体力学软件模拟不但节约了需要做出实际模型的步骤，还能很快得出所需的实验值，同时涡轮的受力情况对其设计具有一定指导意义。

在本文中，采用Fluent 软件对这组模型进行模拟，得出以下结论。

比较各组的压力与流速图可以得出随着开度的减小压力和流速的变化范围有越来越大，也就是流体越来越不稳定。

比较各组的压力与流速图不难发现在流速大的地方压力较小，在流速小的地方压力较大，符合伯努利方程，但是在贴近壁面的地方会因为流体的黏性导致速度减小。

比较各组数据最后受力面收到的力可以得出受力面收到的力都是向下的，加快开度减小的力。并且与开度呈线性变化，假设开度为X，总系数为Y，用最小二乘法可以计算出两者的关系为：Y=-0.1574663005+0.1857328625X，置信率为99.4%。