动态故障树顶事件发生概率的蒙特卡洛近似算法＊

杨恒占，张 可，钱富才

（1．西安工业大学 电子信息工程学院，西安710021；2．西安理工大学 自动化与信息工程学院，西安710048）

动态故障树（Dynamic Fault Tree，DFT）是采用动态逻辑门进行实际物理系统故障诊断的一种方法．自1992年动态故障树模型首次提出起［1］，已在不同领域得到深入的研究．由于动态故障树建模方便、高效，其实际应用也越来越广泛．例如容错计算机、航空电子设备系统、FTPP（容错并行处理器）配置、航天系统等系统的可靠性分析中，大量应用动态故障树计算故障事件发生概率［2-3，10-11］．目前，在动态故障树算法理论研究方面，主要形成了三种算法思路［4］：基于Markov状态转移过程的分析算法、基于贝叶斯网络（Bayesian Network，BN）的分析算法和基于梯形公式的近似分析算法［5-7］．这些方法在不同领域都得到了一定的应用，但普遍存在计算复杂、计算效率低问题，阻碍了在线分析应用，尤其在故障树的规模较大时更为明显．

在动态故障树中，故障事件位于故障树顶部，引起它发生的随机因素很多，而其发生概率就是众多随机变量的概率密度函数在特定区域的积分．这是一个多重积分的计算问题，除非该积分能转化为多个单重积分，否则这类问题的传统算法都会遇到计算爆炸问题，而且随积分维数的增加计算量呈指数增长．这也是传统算法效率低下的根本原因．因此，迫切需要寻找一种简单、高效的求解动态故障树顶事件故障概率的算法．

本文在动态故障树分析过程中应用Monte Carlo方法，将多重积分等价为具有特定分布随机函数的期望值，设计随机实验以获得随机被积函数的样本．

1 动态逻辑模块顶事件发生概率的计算公式

动态故障树由多种动态逻辑门根据实际物理关系组合而成．动态逻辑门包括顺序相关门、优先与门、冷备件门、热备件门和功能相关门．已知一系列随机变量的分布就可以求得这些随机变量函数的分布，因此通过分析动态故障树子树的失效分布就能够得到动态故障树顶事件的失效分布．各种动态逻辑模块失效分布的运算机理为

1．1 顺序相关门

顺序相关门的逻辑功能是当底事件以从左到右的顺序依次发生时顶事件才发生．假设底事件xi（i＝1，2，…，m-1，m）的发生时间Ti的概率分布函数依次为Gi（xi），那么顶事件的发生时间T的概率分布函数GS（t）为

1．2 优先与门

优先与门是顺序相关门输入为两个时的特例，在逻辑上相当于“与门”，但是要求输入事件必须以指定的顺序发生．假设底事件x1和x2的发生时间T1和T2的概率分布函数分别为G1（x1）和G2（x2），则顶事件的发生时间 的概率分布函数GY（t）为

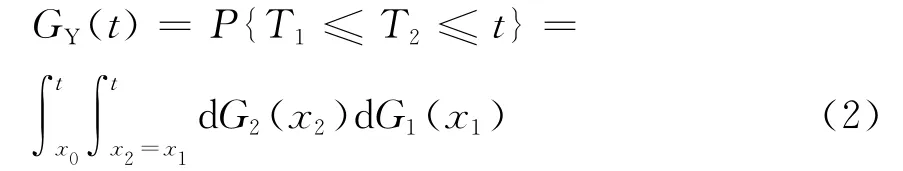
1．3 冷备件门

冷备件门有一个主件和一个备件，且二者都是基本事件．主件一开始就进入工作状态；备件则是指一开始不工作只是作为主件的替代备件，其失效率为零．假设主件x1和备件x2的发生时间T1和T2的分布函数分别为G1（x1）和G2（x2），则顶事件的发生时间的分布函数GL（t）为

1．4 热备件门

热备件门有一个主件和一个备件，且二者都是基本事件．主件与备件同时处于工作状态，负荷分担，主件与备件的失效分布函数基本相同；当主件和备件均失效时，顶事件发生．一般应用在可靠性要求较高系统中．假设主件x1和备件x2的发生时间T1和T2的分布函数分别为G1（x1）和G2（x2），则顶事件的发生时间T的分布函数GR（t）为

1．5 功能相关门

功能相关门的逻辑功能为当触发事件发生时就会引起基本事件发生，则顶事件也会发生；或者基本事件单独发生时，顶事件也会发生．假设触发事件x1和底事件x2的发生时间T1和T2的分布函数分别为G1（X1）和G2（X2），则顶事件的发生时间T的分布GG（t）为

综上分析，多重积分的计算成为动态故障树分析方法的核心问题，而这些积分的计算量过大问题严重制约了动态故障树方法的推广应用．

2 Monte Carlo方法

Monte Carlo方法是指任何利用随机数列来做随机模拟的数值方法，该方法一般通过构造符合一定规则的随机数来解决数学上的各种问题．对于计算过于复杂而难以得到解析解或者根本没有解析解的问题，Monte Carlo方法是一种有效的求出数值解的方法，Monte Carlo方法在数学中最常见的应用就是Monte Carlo积分．许多物理问题都会涉及到多重积分的计算问题，对于这类问题，计算量随维数的增加呈指数增长，传统的数值算法难以求解，Monte Carlo积分方法能很好的求解多重积分问题，实现多重积分的快速计算，因为该方法的计算不依赖于维数．

Monte Carlo方法的解题过程可以归结为三个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量．Monte Carlo求解多重积分发展较成熟的方法主要有两种［8-9］：随机投点法和均值估计法．因为随机投点法的误差较大且做法繁琐，通常不被采用．均值估计法比随机投点法更好操作，精度更高（若选择的密度函数合适）．文中采用均值估计法求解动态故障树中的多重积分，最终得到顶事件发生概率．均值估计法原理．

考虑k重积分

其中Ω为k维积分区域．

选取Ω上的一个概率密度函数g（x1，x2，…，xk-1，xk），使它满足当（x1，x2，…，xk-1，xk）∈Ω时g（x1，x2，…，xk）≠0．

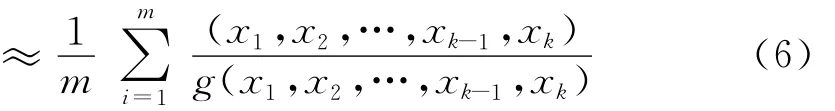
其中m是随机点落在Ω区域中的投点数．

Monte Carlo积分本质在于将积分平均转化为统计平均，因此大大简化了积分计算过程．本文结合某卫星太阳翼驱动机构的步进电机实例，将此方法应用于实际系统中．

3 卫星太阳翼驱动机构步进电机实例分析

该步进电机由定子、转子、轴承、定子绕组等组成，而其易损零部件主要为轴承与定子绕组．为了提高系统的可靠性，航天器机构中的步进电机通常采用双绕组作为备份手段．其中轴承模块包括轴承1和轴承2两个，它们与定子绕组之间为“或门”关系，即其中一个故障，系统失效．定子绕组模块由定子绕组主件和定子绕组备件组成，它们之间是冷备件关系，即主件失效，则启用备件，当备件再失效，则宣布系统失效．

由以上分析可得“步进电机故障”的动态故障树模型如图1所示．

图1 “步进电机故障”DFT模型Fig．1 DFT model for“Stepping motor fault”

图1中A，C，X1和X2为模型的底事件，分别代表轴承1，轴承2，定子绕组主件和定子绕组备件；B为模型的中间事件，代表定子绕组；T为模型的输出事件，代表步进电机失效．

由以上DFT模型可知，顶事件T发生概率为

假设轴承1和轴承2的寿命均服从指数分布，其失效率为1．0×10-6h-1，其失效率函数分别为

假设定子绕组的主件与备件的寿命服从w（100 000，3）分布，其失效概率函数分别为

根据式（3）可得定子绕组的失效概率函数为

选取g（t1，t2）为积分区域Ω上的均匀分布，设Ω的体积为Vs，则

由式（6）和式（10）可转换为

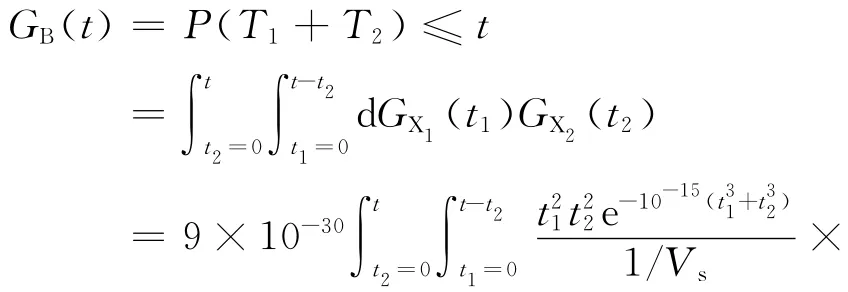
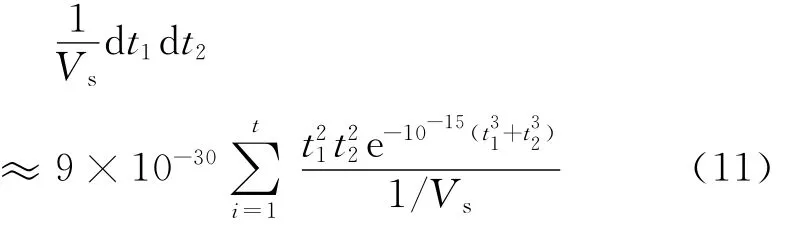
将定子绕组的失效概率函数以及轴承1和轴承2作为顶事件的输入，即可求得“步进电机故障”动态故障树模型顶事件在t时刻的发生概率．

采用Monte Carlo算法在不同时刻编程求解式（11），结合式（7）～（8）求得顶事件T的发生概率．

为了说明本文方法的优越性，针对“步进电机故障”动态故障树模型与梯形公式法进行了仿真结果对比，得出顶事件不可靠度和计算效率的比较结果见表1．

可见，Monte Carlor方法可以应用于实际航天系统中重要的数值积分计算，实现航天系统的故障诊断．应用Monte Carlo方法计算动态故障树顶事件故障概率，简化了计算过程，显著提高了计算效率，并且随着积分维数的增加，Monte Carlo方法性能优势更加明显．

表1 顶事件不可靠度和仿真效率结果比较Tab．1 Comparison between the top event reliability and the computational efficiency

4 结 论

1）本文将Monte Carlo方法应用于动态故障树顶事件发生概率的求解中，将顶事件概率转换为不同的多重积分，把多重积分等价为具有特定分布随机函数的期望值，该样本均值就是多重积分的近似值，设计随机实验以获得随机被积函数的样本，用Monte Carlo方法求出样本均值，实现了动态故障树的定量分析．该样本均值就是多重积分的近似值．

2）通“卫星太阳翼驱动机构步进电机”实例分析与梯形公式法进行比较，本文方法与梯形公式法相比较在计算结果上基本一致，仿真效率比梯形公式法提高了50%，满足动态故障树顶事件发生概率的计算要求．

3）采用Monte Carlo方法进行动态故障树的定量分析，不依赖于积分维数，尤其适用于复杂多维积分问题的求解．能够有效解决动态故障树方法固有的计算困难问题，有效避免了传统故障树分析中“组合爆炸”问题的发生，满足航天系统在线分析的要求．

［1］ DUGAN J B，BAVUSO S J，Boyd M A．Dynamic Fault-Tree Models for Fault Tolerant［J］．IEEE Transactions on Reliability，1992，41（3）：363．

［2］ 范长征，蒋凡，曾凡平．综合故障树分析方法在容错计算机系统中的应用［J］．计算机仿真，2006（4）：63．FAN Chang-zheng，JIANG Fan，ZENG Fan-ping．Aplication of Integrated Fault Tree Analysis to Fault Tree Analysis to Fault-tolerant Computer Systems［J］．The Computer Simulation，2006（4）：63．（in Chinese）

［3］ 邢晓辰，蔡远文，程龙，等．基于故障树的目标航天器在轨故障定位［J］．兵工自动化，2013（10）：71．XING Xiao-chen，CAI Yuan-wen，CHENG Long，et al．On-Orbit Fault Positioning of Tanget Space Craft Based on Fault Free［J］．These Automation，2013（10）：71．（in Chinese）

［4］ 段凌昊，郭爱民，潘勇．动态故障树分析算法研究综述［J］．电子产品可靠性与环境试验，2013（4）：59．DUAN Ling-hao，GUO Ai-min，PAN Yong．Review on Dynamic Fault Tree Analysis［J］．Electronic Product Reliability and Environmental Testing，2013（4）：59．（in Chinese）

［5］ BOUDALI H，DUGAN J B．A Discrete-Time Bayesian Network Reliability Modeling and Analysis Framework［J］．Reli-ability Engineering and System Safety，2005，873：37．

［6］ AMARI S．A New Approach to Solve Dynamic Fault Tree［C］／／Proceeding Annual Reliability and Maintainability Symposium．Alexander：RAMS，2005：374．

［7］ GULATI R，DUGAN J B．A Modular Approach to Analyzing Static and Dynamic Fault Tree［C］／／Proceedings Annual Reliability and Maintainability Symposium．Fort Worth：RAMS，2009：57．

［8］ 马海峰，刘宇熹．基于 Monte-Carlo方法计算定积分的算法研究［J］．计算机与现代化，2011（11）：15．MA Hai-feng，LIU Yu-xi．Research on Calculating Definite Integrals Method Based on Monte-Carlo［J］．Computer and Modern，2011 （11）：15．（in Chinese）

［9］ 方再根．计算机模拟和蒙特卡洛方法［M］．北京：北京工业学院出版社，1988．FANG Zai-gen．Computer Simulation and Monte Carlo Method［M］．Beijing：Beijing Industrial Institute Publishing House，1988．（in Chinese）

［10］ 梅启智．系统可靠性工程基础［M］．北京：科学出版社，1992．MEI Qi-zhi．System Reliability Engineering Foundation［M］．Beijing：Science Press，1992．（in Chinese）

［11］ 吴嘉宁，阎绍泽，谢里阳．基于RBD和FTA的航天器太阳翼可靠性分析［J］．清华大学学报：自然科学版，2012（1）：15．WU Jia-ning，YAN Shao-ze，XIE Li-yang．Reliability Analysis of Spaceraft Solar Arrays Based on RBD and FTA［J］．Journal of Tsinghua University：Science and Technology，2012（1）：15．（in Chinese）