落点预测制导律的旋转稳定弹修正控制*
黎海青,杨 凯,栗金平,王 冬,马 菲
(中国兵器工业第203研究所,西安710065)
弹道修正技术是对常规弹药制导化的有效措施,对提升武器作战效费比具有重大意义.主要方法是在普通炮弹引信上加装或改装弹道修正模块,在飞行过程中测量弹丸位置、速度等信息,利用执行机构改变弹丸弹道,提高命中精度[1].目前,美国、英国、以色列等国家均在开展旋转稳定弹弹道修正技术研究.
旋转稳定弹的特性决定了其可用过载较小,故传统制导律往往不适用于此类弹.关于旋转稳定双旋弹建模、制导律设计等方面的研究资料较少,文献[2-4]对旋转稳定双旋弹进行了初步建模,并对飞行稳定性进行了仿真分析;文献[5-7]采用复合修正方式修正控制,但无法实现连续修正,修正精度不高.文中采用落点预测制导律,对旋转稳定炮弹进行修正控制.针对一类采用固定翼控制的双旋结构旋转稳定弹建立弹道运动方程,研究基于四自由度(4D)质点模型的落点预测算法,并在此基础上设计旋转稳定弹制导律,给出弹道仿真计算结果,实现对旋转稳定炮弹的修正控制.
1 旋转稳定弹运动方程
带固定翼旋转稳定弹由前体和后体两部分组成.前体表面安装两对翼,一对同向翼提供升力,一对差动翼用于减旋;后体相对惯性系高速旋转,保持弹体稳定,如图1所示.以下建立其动力学和运动学方程.

图1 带固定翼修正机构的旋转稳定弹示意图Fig.1 Schematic diagram of spin-stabilized projectile equipped with fixed-wing
1.1 旋转稳定弹动力学方程
弹丸动力学方程可以表示为


1.2 旋转稳定弹运动学方程
在地面坐标系下的运动关系式可以表示为

式中:αw、βw、θw、ψvw分别为攻角、侧滑角、弹道倾角、弹道偏角;Vx、Vy、Vz为x、y、z方向上的空速.
旋转稳定弹的特点是前后体双旋,它的转速不同,其极阻尼力矩也不同,并且前体表面安装有差动减旋翼,所以前体还受到导转力矩作用,因此将前后体在弹轴方向运动分开研究.
假设旋转稳定弹前、后体各自的惯性主轴与全弹中心惯性主轴是平行的,由牛顿第二定律和动量矩定理可推导出绕质心动力学方程为

式中:JxF为前体弹轴方向的转动惯量;JxA为后体弹轴方向的转动惯量;ωxF为前体弹轴方向的角速度;ωxA为后体弹轴方向的角速度;MxF为前体弹轴方向受到的合外力矩;MxA为后体弹轴方向受到的合外力矩;MV为后体作用于前体的滚转约束力矩在弹轴方向的分量.
绕质心运动学方程变为
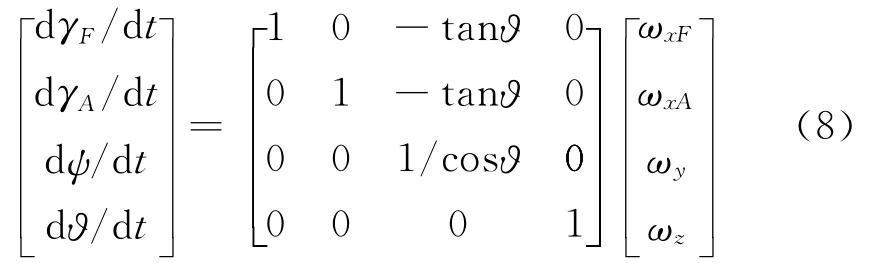
式中:γF为前体滚转角;γA为后体滚转角.
2 基于4D模型的落点预测算法
完整的旋转稳定弹弹道方程比较复杂,计算工作量大,为满足修正炮弹弹上解算实时性要求,在一定假设条件下可以利用相对简单的旋转稳定弹4D质点弹道模型来预测落点,其运动方程为

式中:X为状态变量;ρ为空气密度;S为弹丸横截面积;V为速度;FD为阻力符合系数;CD0为零升阻力;CD为诱导阻力系数;Cl为升力系数;αe为动力平衡角;F为马格努斯力;G为重力;P为滚转角速度;C为滚转角加速度系数;d为弹径;Clp为滚转阻尼力矩系数[10].
进行落点预测时,计算初始条件为已知量,由测量弹道获得,将参数X(t0)作为初始值,采用迭代解微分方程预测后续弹道并计算落点.
3 落点预测制导律设计
3.1 落点预测制导律
落点预测制导律是以每一时刻弹丸所处的空间位置作为起始点,根据此时的位置、速度等信息计算弹丸在无控状态下的落点位置,并与目标点位置进行对比,利用偏差值E作为反馈形成制导指令的方法.落点预测制导律原理示意如图2所示.
由图2可知,制导指令为


式中:Rld为预估落点矢量;ex、ez为落点在x、z方向上的偏差;xld、zld为落点在发射系下坐标;RT为目标矢量;xT、zT为目标在发射系下坐标.

图2 落点预测制导律示意图Fig.2 Schematic diagram of impact point predication guidance law
采用固定翼作为控制执行机构,通过控制升力翼面横滚姿态角,使其稳定在某个方向产生修正力Fc,从而实现弹道修正.这就要求修正力方向φc尽量与落点偏差矢量方向σ一致,如图3所示,则横滚姿态指令为


图3 落点预测法原理示意图Fig.3 Schematic diagram of impact point predication
3.2 控制参数ε值确定
以目标为圆心,控制参数ε为半径做一个圆,当预测到实际落点落于该圆之外时才进行修正.ε取值与单周期内修正能力有关,而单周期内修正能力Rxz与弹丸高度H、速度v、升力翼面偏角δ及作用时间T等参数相关,即有ε=f(v,H,δ,T)[11].
控制参数ε作为修正开关,将影响弹道最终修正精度.ε取值过大,落点与目标点距离会增大;ε取值过小,会造成控制超调.修正力为
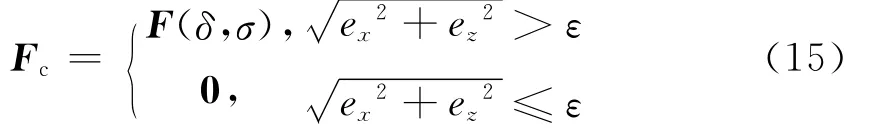
其中F(δ,σ)为修正力函数.
4 仿真及分析
4.1 飞行仿真
文中旋转稳定弹飞行过程包括无控和有控两个阶段.弹丸出膛后,进入无控飞行,此时升力翼面自由转动;10s后卫星定位仪完成搜索并定位,开始修正控制,考虑精度要求,控制参数ε取为10m.基于落点预测制导律的弹道修正仿真条件见表1.

表1 飞行仿真条件Tab.1 Flight simulation conditions
基于落点预测制导律的旋转稳定弹飞行仿真结果如图4~7所示.

图4 弹道高度Fig.4 Trajectory height
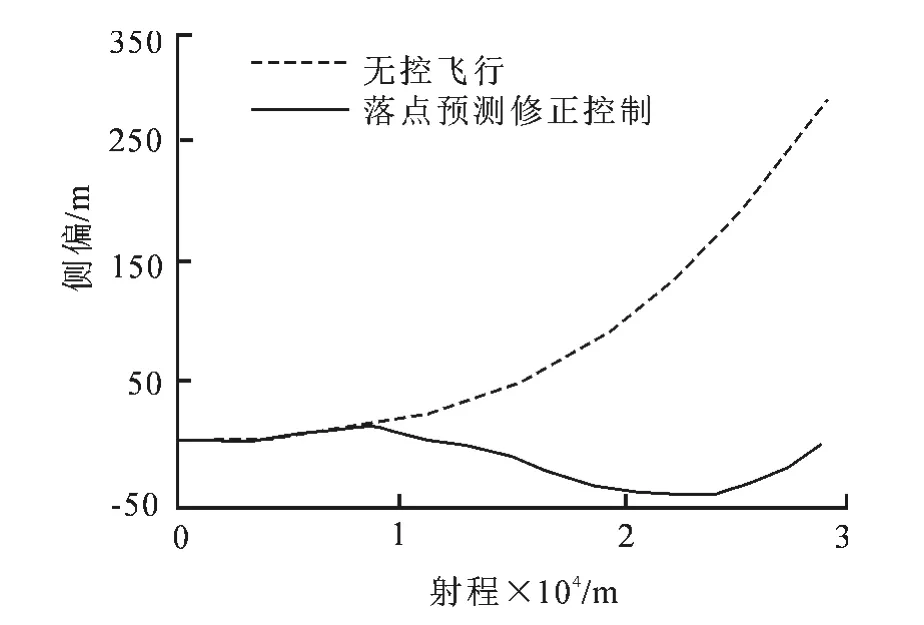
图5 弹道侧偏Fig.5 Trajectory cornering amount
图4~5为弹丸无控状态和在固定翼控制下的弹道运动高度和侧偏.当弹丸飞行至射程为7.3 km处,有控弹道与无控弹道开始分离,并逐渐向目标位置靠近,表明利用落点预测制导律能够有效进行弹道修正,控制旋转稳定弹飞向目标.

图6 飞行速度Fig.6 Flight speed

图7 制导指令Fig.7 Guidance instruction
由图6可知,无控弹与有控弹速度差很小,表明修正控制对弹丸飞行速度影响不大.图7为制导指令的变化曲线.由图7可见,飞行前10s弹丸落点与目标偏差较大,该段无控;10s后,落点偏差开始快速减小,30s时偏差已收敛至20m以内,表明弹道修正控制效果较好.
4.2 蒙特卡罗精度分析
射击精度仿真时考虑平面风、初速、射角以及射向等误差因素的影响,见表2.
利用蒙特卡洛算法分别对无控情况和有控情况进行1 000次模拟仿真,落点散布如图8~9所示.旋转稳定弹精度仿真无控情况圆概率误差(Circular Error Probable,CEP)为253m,有控情况CEP为20 m.由仿真结果可知,用落点预测制导律可大幅减小落点散布,射击精度得到较大提高.

表2 误差因素及分布规律Tab.2 Error factors and distribution model
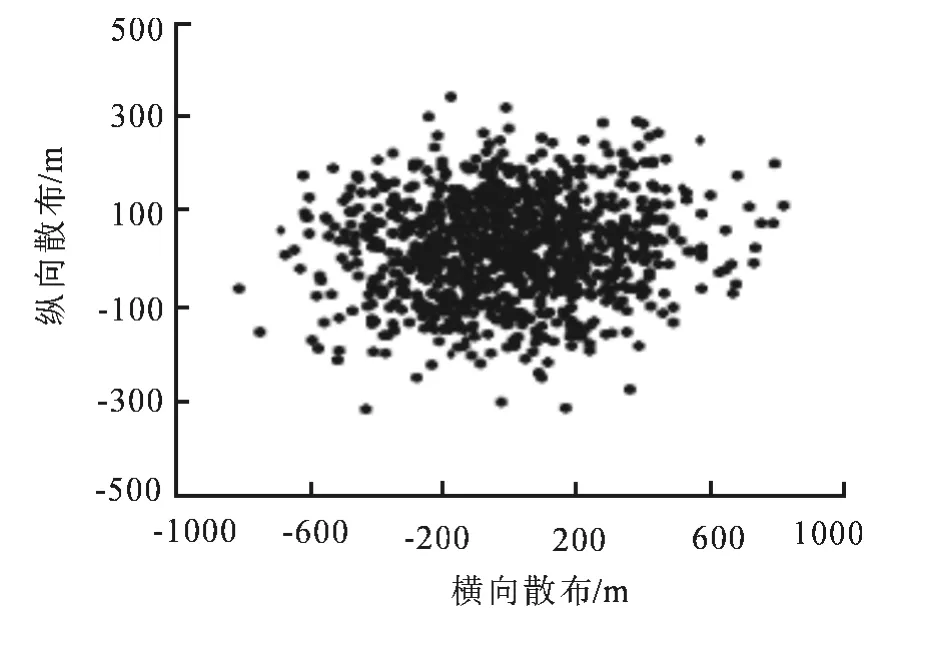
图8 无控落点散布图Fig.8 Impact scatter diagram of uncontrolled
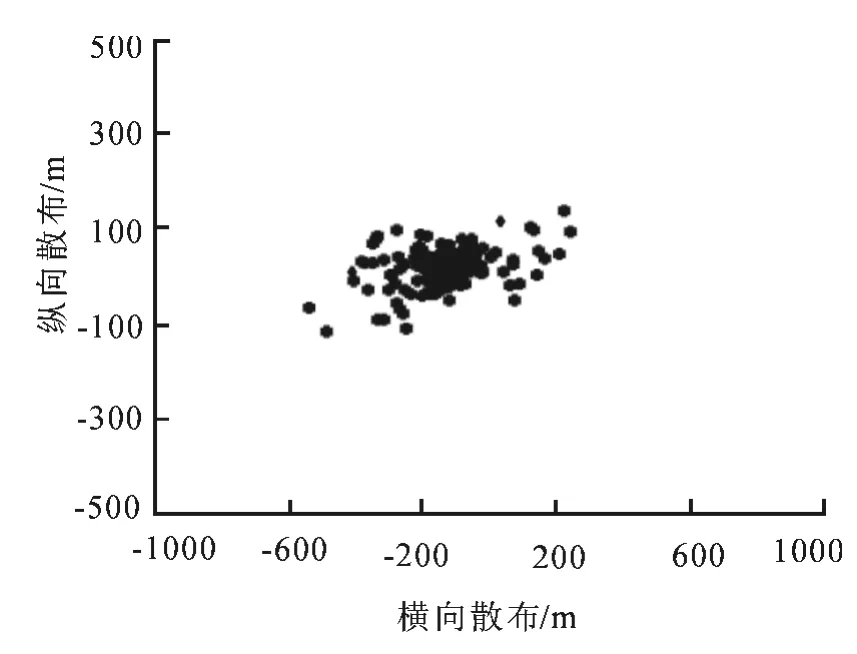
图9 有控落点散布图Fig.9 Impact scatter diagram of controlled
5 结 论
1)通过建立带翼修正机构的旋转稳定弹七自由度运动方程,给出了基于4D修正质点弹道模型的落点预测制导律.
2)基于落点预测制导律修正方式相比无控弹,CEP由235m减小到20m,有效提高了落点精度,为旋转稳定弹的修正控制提供参考.
3)文中简化了前体滚转姿态控制,后续研究可进一步分析其对旋转稳定弹修正控制的影响.
[1] 余勃彪,严平.弹道修正弹弹药现状及关键技术[J].四川兵工学报,2011,32(4):37.YU Bo-biao,YAN Ping.The Actuality of Ammunition for Ballistic Trajectory and Its Key Technology[J].Journal of Sichuan Ordnance,2011,32(4):37.(in Chinese)
[2] 揭涛,施坤林.旋转稳定弹弹道修正引信减旋装置研究[J].探测与控制学报,2007,29(5):9.JIE Tao,SHI Kun-lin.Study on Despining Device of Course Correction Fuze for Spin-Stabilized Projectile[J].Journal of Detection & Control,2007,29(5):9.(in Chinese)
[3] 常思江,王中原,刘铁铮.鸭式布局双旋弹飞行动力学建模与仿真[J].弹道学报,2014,26(3):1.CHANG Si-jiang,WANG Zhong-yuan,LIU Tiezheng.Modeling and Simulation of Flight Dynamics for Dual-Spin Stabilized Projectile Equipped with Canards[J].Journal of Ballistics,2014,26(3):1.(in Chinese)
[4] WERNERT P.Stability Analysis for Canard Guided Dual-Spin Stabilized Projectiles[C]//AIAA Atmospheric Flight Mechanics Conference.Chicago:AIAA Atmospheric Flight Mechanics Conference,2009:10.
[5] 史金光,王中原,常思江,等.基于减旋控制的侧向弹道修正技术[J].弹道学报,2010,22(3):81.SHI Jin-guang,WANG Zhong-yuan,CHANG Si-jiang,et al.Technology of Lateral Trajectory Correction Based on Spin Velocity Reduction Control[J].Journal of Ballistics,2010,22(3):81.(in Chinese)
[6] 霍鹏飞,杨小会,刘创.基于减旋的弹道横偏修正方法反求分析[J].探测与控制学报,2008,30(6):12.HUO Peng-fei,YANG Xiao-hui,LIU Chuang.Deflection Error Correction Method for Spin-Stabilized Projectiles Based on Despining Approach[J].Journal of Detection & Control,2008,30(6):12.(in Chinese)
[7] 史金光.王中原.常思江,等.二维弹道修正弹修正方法[J].海军工程大学学报,2010,22(4):87.SHI Jin-guang,WANG Zhong-yuan,CHANG Si-jiang,et al.Investigation on Control Methods for Two-Dimension Trajectory Correction Projectiles[J].Journal of Naval University of Engineering,2010,22(4):87.(in Chinese)
[8] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000.QIAN Xing-fang,LIN Rui-xiong,ZHAO Ya-nan.Missile Flight Aerodynamics[M].Beijing:Beijing Institute of Technology Press,2000.(in Chinese)
[9] 闫章更,祁载康.射表技术[M].北京:国防工业出版社,2000.YAN Zhang-geng,QI Zai-kang.Firing Table Technology[M].Beijing:National Defense Industry Press,2000.(in Chinese)
[10] JOHN A,PRAIRIE C E.Fixed Canard 2DGuidance of Artillery Projectiles:US,6981672B2[P/OL].2006-01-03[2006-08-12].http://patft.uspto.gov.
[11] FRANK J R.Aeroballistics of a Terminally Corrected Spinning Projectile (TCSP)[J].Spacecraft,1975,12(12):733.

