某水电站面板堆石坝三维有限元变形分析＊

梁昕宇，张 英，党发宁

（1．西安工业大学 建筑工程学院，西安710021；2．贵州电力职业技术学院 贵州电网公司培训与评价中心，贵阳550001；3．西安理工大学 土木与建筑学院，西安710048）

中国自1985年以来引进国外先进坝工技术和经验，混凝土面板堆石坝成为水利水电行业普遍采用的主坝型．这种坝型在工程实践中体现出更好的经济性、安全性和适应性，成为当前首选的坝型，国际大坝委员会不完全的统计，中国混凝土面板堆石坝的总数已经占全世界的50%以上，在大量和大型的混凝土面板堆石坝工程的应用中，提出了高坝变形安全的理念，提出了较为合理的坝体分区和有利于高坝防渗体系-面板与接缝止水的变形安全和渗流安全［1-2］．

基于止水设计，提出了高坝的周边缝止水结构和止水材料．并结合数值计算进行分析和研究．采用非线性有限元法计算混凝土面板堆石坝变形应力的成果较多［3-8］．文献［5］采用三维有限元数值分析方法研究了超高混凝土面板堆石坝的变形规律；文献［6］根据混凝土面板堆石坝的特点，提出了一种计算机数值和图形模拟方法；文献［7］利用考虑剪胀性和应变软化性的K-G模型和目前应用较广泛的E-μ模型对紫坪铺混凝土面板堆石坝进行了二维有限元应力-应变对比计算分析；文献［8］基于ABAQUS二次子程序开发，对某贴坡型混凝土面板堆石坝施工填筑期和水库蓄水运行期的应力和变形进行模拟分析．本文基于有限元分析软件ANSYS二次开发平台，采用邓肯-张E-B本构模型进行了坝体应力与变形分析．在混凝土面板堆石坝数值计算分析中，基岩、山体、面板、趾板和灌浆帷幕采用线弹性模型；过渡层，垫层，主堆石，次堆石及坝基砂砾石层等材料采用非线性弹性邓肯-张E-B模型，为某水电站面板堆石坝的设计和决策提供依据．

1 工程概况

某水电站混凝土面板堆石坝坝顶高程2 860．00m，顶部设3．7m高“L”型钢筋混凝土防浪墙，墙顶高程2 861．2m，趾板基础高程2 716 m，最大坝高144．00m，上游坝坡1∶1．4，下游综合坝坡1∶1．5，坝顶宽10m，坝底最大宽度447 m，坝顶长度290m，按2级建筑物设计．趾板为平趾板，河床、两岸趾板均置于强风化下部，厚度0．6 m，按作用水头不同，2 820m以上趾板宽度4m、以下7m，设伸缩缝，趾板与地基的联接设置锚筋，锚筋采用梅花型布置，长4．5m，伸入基岩3．7m，直径∅28mm，间距1．2～1．5m．混凝土面板顶部厚度0．3m，底部厚度0．72m，两岸受拉区每6m设垂直缝一条，河床受压区每12m设垂直缝一条．接缝包括周边缝、面板张性缝、面板压性缝、面板与防浪墙间的伸缩缝、防浪墙间的伸缩缝以及趾板间的伸缩缝，各缝型按其受力变形特点分别设置相应的止水措施．

2 计算参数确定和模型的建立

2．1 计算参数确定

计算涉及到10种材料，其中过渡层，垫层，主堆石，次堆石及坝基砂砾石层材料计算参数见表1．其中φ为内摩擦角，Δφ为摩擦角误差，K、Kur、n、Kb、m、Rf为E-B模型参数．

2．2 接触面单元

面板与垫层之间采用面-面接触单元（无厚度）以模拟接触特性，趾板与面板（周边缝）、面板与防浪墙之间及面板间垂直缝采用分离缝模型．

2．3 计算模型的建立

模型采用空间四面体单元与空间六面体等参数单元．基岩、山体、面板、趾板和灌浆帷幕采用线弹性模型；过渡层，垫层，主堆石，次堆石，坝基砂砾石层等材料宜用非线性弹性邓肯-张E-B模型．模型的四周采用水平法向约束，底部采用全约束．网格划分情况如图1所示．

2．4 计算荷载及工况

计算中，大坝自重采用分级加载方法，将大坝自重分为15级载荷逐步施加，每层最大施加高度为15．0m．面板分两步施工模拟．水载荷分为死水位、正常蓄水位和校核洪水位三种工况．

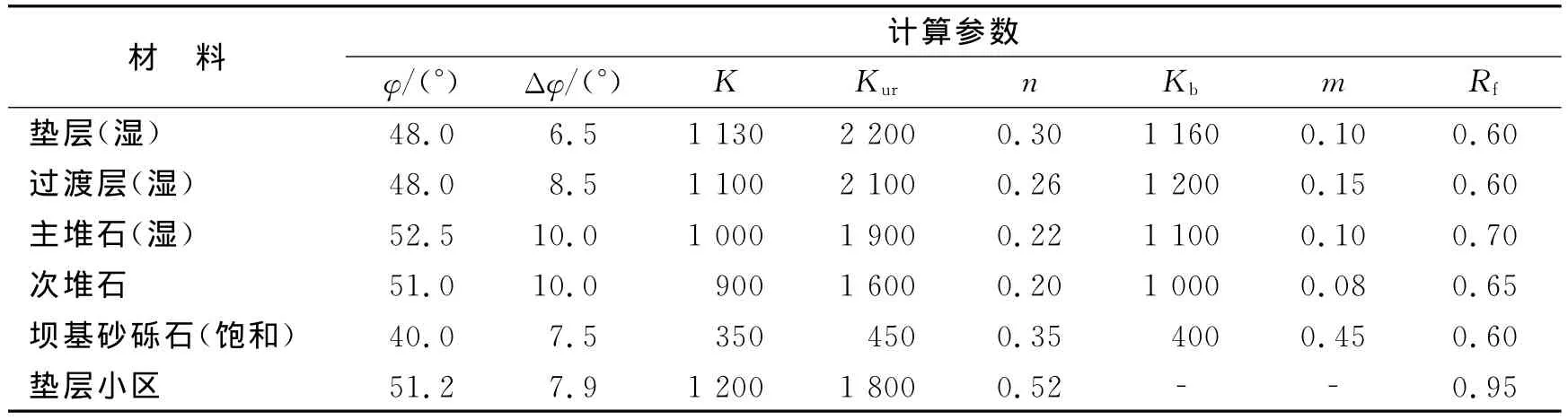
表1 坝料、覆盖层计算参数（E-B模型）Tab．1 The calculation parameters of dam material and cover layer（E-Bmodel）

图1 计算模型Fig．1 Computation model

计算严格按照设计方提供的施工程序（填筑、浇筑及蓄水过程等）进行计算，整个加载过程按施工程序分步进行计算，同时，考虑库水与面板的相互作用，以确保计算结果的精度及合理性．计算中大坝填筑、面板铺设和水压力施加共分16步进行，蓄水过程按死水位 22 805．00m、正常蓄水位22 857．00m的步骤进行，从竣工期至正常蓄水位分6步均匀进行．在三维有限元计算分析的模型构造中，整个坝体沿坝轴线将整个坝体分成38个横断面，各横断面的位置与面板的垂直缝一致．横断面的位置及四个垂直于大坝轴线的剖面位置如图2所示．顶面数字1～38为横断面位置编号．

面板编号以及垂直缝和周边缝的编号如图3所示，图3中顶面数字1～38为面板垂直缝编号，侧面及底面编号为周边缝编号，中间编号为面板编号．

图2 坝体应力与变形分析剖面位置图Fig．2 The section of dam stress and deformation

图3 面板应力与变形分析中面板编号Fig．3 The number of panel stress and deformation

3 计算结果及分析

3．1 竣工期坝体应力变形

按材料力学中的符号规定，应力以拉为正，以压为负．大坝施工到2 857．5m高程时是数值模拟的大坝蓄水前的最后一步施工，三维有限元计算结果如图4所示．

由于1-1剖面位于河床中心，该剖面为梯形分布，上游综合坡度略大于下游坡度，故该剖面上游水平位移比下游侧向位移要大一些，上游侧向最大水平位移为16．05cm，而下游侧向最大水平位移为12．48cm．该剖面蓄水前最大沉降为126．1cm，最大沉降位于坝轴线下方1／3坝高的堆石体内．

大坝蓄水前2 857．5m高程时坝体应力为堆石体自重应力场分布，不同坝段的应力大小主要与坝体的填筑高度有关，坝体上下游侧面的水平向水平应力基本上呈对称分布．坝体的水平、垂向应力比较规则，呈连续的变化，基本上全部为压应力．同时坝体垂向应力呈现从坝顶到坝底逐步增加的趋势，最大垂向应力发生在坝底，1-1剖面最大垂向应力为1．99MPa．

3．2 正常蓄水位大坝应力变形

水库从死水位2 805．00m蓄水到正常蓄水位2 857．00m高程，大坝进入正常蓄水位．大坝正常蓄水位时的应力与位移计算结果如图5所示．

由图5看出，水库到达正常蓄水位后，在水荷载水平和垂直分力的作用下，坝体整体向下游变形，上游的侧向水平位移均有一定减小，下游侧向水平位移均有一定程度增大，且坝体的沉降量也有明显的增加．1-1剖面上游侧向最大水平位移为12．6cm，比竣工期减小了3．4cm，下游一侧的最大水平位移为18．1cm，比竣工期增加了5．7cm．同时说明水压力对坝体的水平位移影响较大，在水压力的作用下，坝体上游侧向的水平位移均指向下游，下游侧向水平位移有明显的增大．从坝体沉降量看，蓄水后坝体1-1剖面（1-1剖面所在位置如图2所示）的最大沉降量为147．5cm．

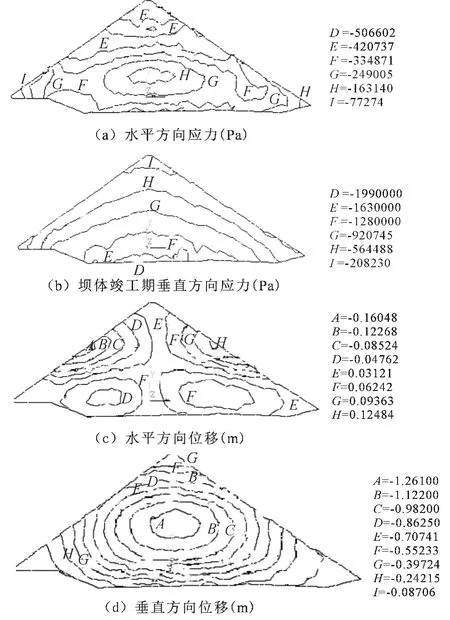
图4 坝体竣工期应力与位移图Fig．4 Stress and displacements of construction

从坝体蓄水期1-1剖面处的变形情况来看，最大沉降量均比竣工期有较大幅度的增加，由于水压力的作用，大坝上游一侧的水平位移最大值均有不同程度的减小，而下游一侧的水平位移最大值均有不同程度的增加．

蓄水期，在自重和水压力联合作用下，坝体的水平、垂向应力都有所增加，特别是坝体上游侧向大、小主应力的增幅比较明显．蓄水后坝体的水平、垂向应力呈连续的变化，1-1剖面最大垂向应力为2．24MPa，大、小主应力最大值分别为2．33MPa、0．478MPa．

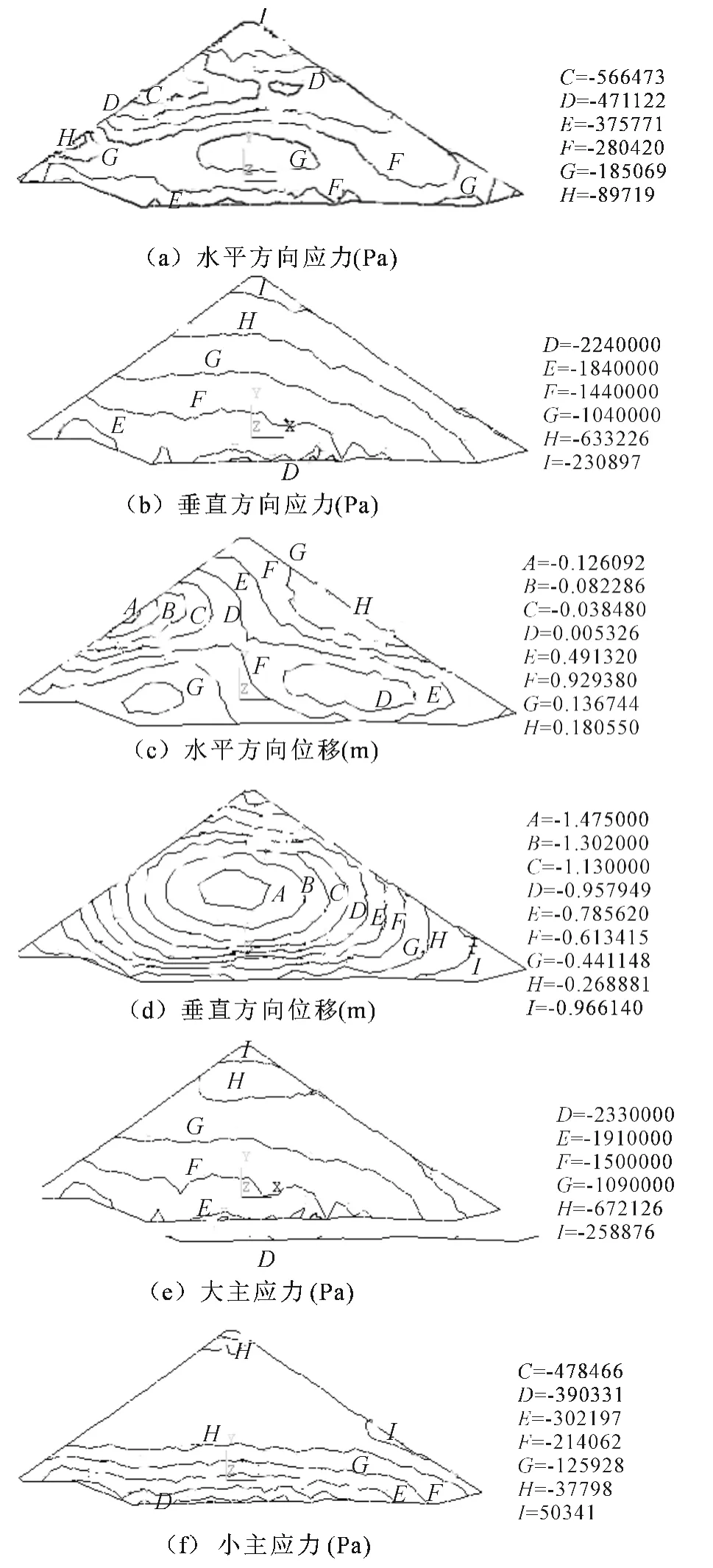
图5 坝体蓄水期应力与位移Fig．5 Stress and displacements of operation periods

3．3 面板应力变形计算结果分析

面板的应力与变形计算结果如图6所示，由图6（a）可见，面板水平位移自两岸向中间变形，其左侧面板最大位移量为15．2mm，右侧面板最大位移量为15．8mm，河床两侧面板变形基本对称，左侧略大于右侧．面板水平位移分布呈从两岸向河床中部位移减小的趋势．面板水平位移零线的位置基本上处于河谷中央附近．从位移变化的梯度上看，由于右岸坝体部分地形相对较陡，因此，右岸面板变形梯度相对较大．面板挠度等值线如图6（b）所示，由图6（b）可见，当水库蓄水到正常蓄水位时，计算所得面板最大挠度为14．88cm，位于1／2坝高左右，靠近面板中心位置．虽然面板挠度分布与坝基面形态有关，但计算结果表明面板各个方向的挠度分布比较均匀．

图6 面板的应力和位移Fig．6 Stress and displacements of panel

与面板水平位移相对应，面板水平向应力（坝轴线方向）表现为中间受压、两岸边很小范围周边缝受拉的特性．图6（c）为面板水平向应力等值线，计算结果显示，面板大部分区域承受压应力作用，拉应力仅在左右岸边附近局部区域出现．坝轴向压应力最大值为6．73MPa，位于约1／2坝高处，拉应力最大值为0．618MPa，位于左岸和右岸岸坡附近．面板坝轴向压应力和拉应力均比较大，这是由于面板受到水压力作用后，产生的弯曲应力与自重应力叠加所致．面板在垂直缝和周边缝处应力分布有突变，因此，面板上的应力等值线不够光滑．

图6（d）为面板顺坡向应力等值线，计算结果显示，由于面板在水压力的作用下发生一定程度的弯曲变形，因此，沿坝坡方向面板也主要承受压应力，且中部压应力较大，而面板底部则主要承受拉应力，最大顺坡向压应力为7．25MPa，顺坡向拉应力仅出现在面板底部局部区域，最大拉应力值为1．7MPa．

从面板应力与变形计算结果来看，面板挠度和水平位移值都不大，面板应力分布规律合理，面板中压应力最大值不超过10MPa，拉应力只发生在局部区域，且拉应力值总体不大．但面板顺坡向拉应力最大值达到1．7MPa，应引起重视，应当提高这部分混凝土的强度．

3．4 面板垂直缝和周边缝变形计算结果分析

在正常蓄水位作用下，面板堆石坝垂直缝的受力特点因其所处的位置不同差异很大，河床段垂直缝基本以压缩为主，岸坡段垂直缝则以张拉为主，这主要是因为河床段坝体的断面较岸坡段坝体断面要大一些，因此，在施工期、蓄水期及后期，河床段坝体的沉降要较两侧岸坡段坝体的沉降要大一些，两岸段坝体由于侧向约束的减弱将向中心发生相对位移，从而使中间部位的垂直缝受压，而两岸的垂直缝受拉．图7为计算的垂直缝张拉变形值，面板垂直缝最大张拉变形量为5．4mm，位于20号缝附近（计算模型中该位置为坝体填筑区域变化较大处），面板垂直缝最大沉陷变形量为9mm．面板的垂直缝最大沉陷变形量大于最大张拉变形量和最大剪切变形量．

周边缝位于趾板与面板两种变形性质差异较大的界面上，由于两者的不连续，工作条件最差，是面板坝中对变形最敏感、防渗最关键的部位．在施工期及蓄水期，当堆石体产生较大的变形时，周边缝会产生相应的三向位移．蓄水期趾板一方面要受到防渗墙顶部传来的水平推力，另一方面要受到上游水压力的作用，其基本变位是向右下方发生位移，位移值的大小，主要与趾板本身所处的位置有关．在上游水头的作用下，面板将水压力依次传递给垫层、过渡层、主堆石区及下游次堆石区，堆石区在水压力的作用下将会产生变形，这些都会引起面板在水压力的作用下向下游发生变位．再者，在水压力作用下面板会向河床中间部位发生位移，而趾板一般不会发生平行其走向方向的位移，即使在该方向发生了位移，一般也不会与面板的挤压变位一致，所以面板会产生相对于趾板的剪切变位．综上分析，在蓄水期面板会产生相对于趾板的沉降、剪切及张拉变位，周边缝止水结构也必将承受沉降、剪切及张拉三向变位．

图7 面板垂直缝变形量（mm）Fig．7 The deformation of vertical joint of panel（mm）

根据有限元分析结果，在周边缝三向变位中，在河谷段周边缝的沉降变位最大，而在岸坡陡峻或坡角变化比较大的部位，张拉变形比较大．面板周边缝三向变位最大值具体如下：其沉降位移最大值为11．2mm，沿岸坡方向的剪切位移最大值为5．3 mm，垂直岸坡方向的张开位移最大值为10．3 mm，分别位于f7、f9和f8缝．其规律性为河床深部位置周边缝张开沉陷量均大于上部周边缝，右边周边缝大于左边，这是因为周边缝的变形主要受坝基形态和水压力的影响．

4 结 论

1）周边缝变位由对称岸坡的两岸受拉变为左岸受挤压而右岸受拉，其周边缝变位与已建工程接近，均在正常范围内．

2）从坝体位移分布趋势和蓄水期面板的应力、变形分布上看，岸坡地形对坝体和面板的应力变形有着明显的影响．右岸陡边坡及凸山梁，引起坝体和面板的变形梯度均较大，对面板的应力状态产生了一定程度的不利影响．但坝体在蓄水期的大、小主应力，面板的最大挠度以及应力变形均在合理范围．

［1］ 郦能惠．高混凝土面板堆石坝新技术［M］．北京：中国水利水电出版社，2007．LI Neng-hui．Recent Technology for High Concrete Face Rockfill Dams［M］．Beijing：China Water Power Press，2007．（in Chinese）

［2］ 郦能惠．高混凝土面板堆石坝设计新理念［J］．中国工程科学，2011，13（3）：12．LI Neng-hui．New Concept of Design for High Concrete Face Rockfill Dams［J］．Engineering Sciences，2011，13（3）：12．（in Chinese）

［3］ 刘祖典，党发宁．土的弹塑性理论基础［M］．西安：世界图书出版公司，2002．LIU Zu-dian，DANG Fa-ning．Plasto-Elastic Theory Bases on Soils［M］．Xi’an：World Publishing Corporation，2002．（in Chinese）

［4］ 钱家欢，殷宗泽．土工原理与计算［M］．2版．北京：中国水利水电出版社，1996．QIAN Jia-huan，YIN Zong-ze．Geotechnical Principles and Calculation［M］．2nd ed．Beijing：China Water Resource and Hydro-Power Press，1996．（in Chinese）

［5］ 郦能惠，孙大伟．300m级超高面板堆石坝变形规律的研究［J］．岩土工程学报，2009，31（2）：155．LI Neng-hui，SUN Da-wei．Deformation Behavior of 300mHigh Concrete Face Rockfill Dams［J］．Chinese Journal of Geotechnical Engineering，2009，31（2）：155．（in Chinese）

［6］ 彭宣茂，李太生．混凝土面板堆石坝三维仿真分析［J］．岩土力学，2003，24（5）：767．PENG Xuan-mao，LI Tai-sheng．Three-Dimensional Simulation Analysis of Concrete Face Rockfill Dam［J］．Rock and Soil Mechanics，2003，24（5）：767．（in Chinese）

［7］ 孙陶，高希章，杨建．紫坪铺混凝土面板堆石坝应力-应变分析［J］．岩土力学，2006，27（2）：247．SUN Tao，GAO Xi-zhang，YANG Jian．Stress-Strain Analysis of Zipingpu Concrete Faced Rockfill Dam［J］．Rock and Soil Mechanics，2006，27（2）：247．（in Chinese）

［8］ 潘家军，徐远杰．贴坡型混凝土面板堆石坝三维非线性分析［J］．岩土力学，2008，29（s1）：113．PAN Jia-jun，XU Yuan-jie．3DNonlinear Analysis of Fitting-Slope Concrete-Face Rockfill Dam［J］．Rock and Soil Mechanics，2008，29（s1）：113．（in Chinese）