风电机组齿轮箱温度预测中输入变量的选择及仿真*
张 舰,李郁侠
(西安理工大学 水利水电学院,西安710048)
齿轮箱温度是风力发电机组状态监测十分重要的监测项目,而齿轮箱温度预测性监测是近几年新兴的监测方法,它对齿轮箱温度监测及预警起到了更好的效果,是未来齿轮箱监测的发展趋势[1].
在齿轮箱温度预测的过程中,输入变量的选择直接关系到预测的准确性.在国内外文献中,对于温度预测过程中的输入变量选择问题研究较少,一般都是通过直接选取来确定.如文献[2]中在建模时直接通过经验选取了机组功率、环境温度、齿轮箱轴承温度以及机舱温度作为建模的输入变量;文献[3]中在建模时选择了齿轮箱轴承温度、发电机功率以及机舱温度直接作为建模的输入变量,这样选择的输入变量在预测时存在局限性,并不能适应所有机组的状况,所得出的预测结果必然不是最优的,因此通过经验直接选取输入变量并不具有科学性;文献[4]也仅仅应用了相关分析法这种比较简单的输入变量选择方法,容易漏选一些重要的输入变量.因此,在齿轮箱温度预测中引入科学的输入变量选择方法,是当前应该主要解决的问题.目前输入变量选择的方法十分繁多,相关分析法[5]、相空间嵌入法[6]、回归分析法[7]、正交最小二乘法[8]都是行之有效的方法.这几种方法各有优缺点,其中相关分析法和回归分析法是常规的方法,它们可以从众多的备选影响因素集中选出一些与期望输出相关度大的因素作为输入变量,由于选出的输入变量之间一般相关度较大,可能会漏选一些重要的相关变量,因而难以取得理想的效果;相空间嵌入法则只能在负荷序列中寻找预测时刻最大的负荷点,对于环境温度、风速等随机的相关变量处理比较困难,需要增加时间变量和环境变量来改善预测效果.相较以上方法,文中利用正交最小二乘法(Orthogonal Leasdt Squares,OLS)对各输入变量进行正交变化,得出各输入变量对输出变量的单独贡献,适合齿轮箱温度预测中输入变量的选择.
1 OLS法原理分析
OLS法在线性回归模型回归算子选择方面具有优异性能,已经成功应用于径向基函数神经网络RBF节点中心选取[9]和模糊系统输入空间划分[10]中.
输入向量组合成的矩阵P是回归矩阵,输入变量的选择为一个线性回归模型为
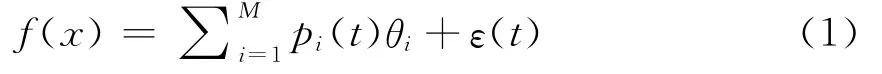
式中:pi(t)为期望输出,也称相关变量;θi为参数;pi(t)为回归算子.输入变量选择问题即在一个给定的M个备选回归算子集合中,选择出一组重要的回归算子.式(1)写成矩阵形式为

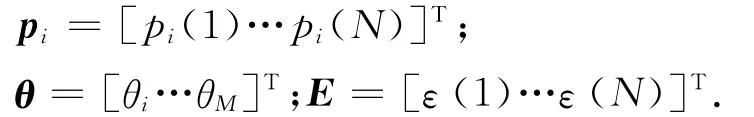

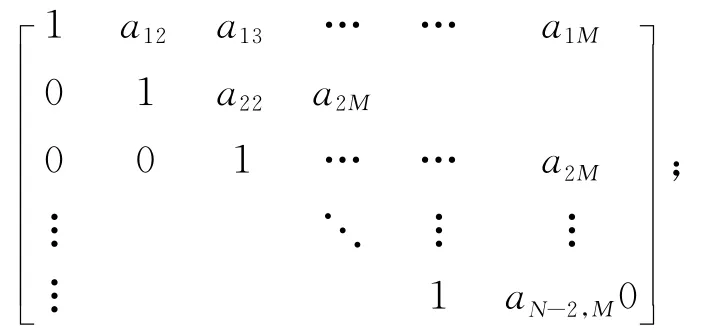
式中:A为M×M上三角矩阵,且对角元为1,A=
W为M×M矩阵,其各列正交:WTW=H,H为对角元素为h1的对角阵;
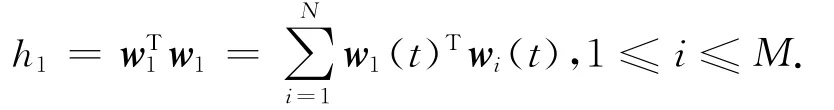
由这组正交基矢量w1张成的空间与pi张成的空间相同,故式(2)为

正交LS解为


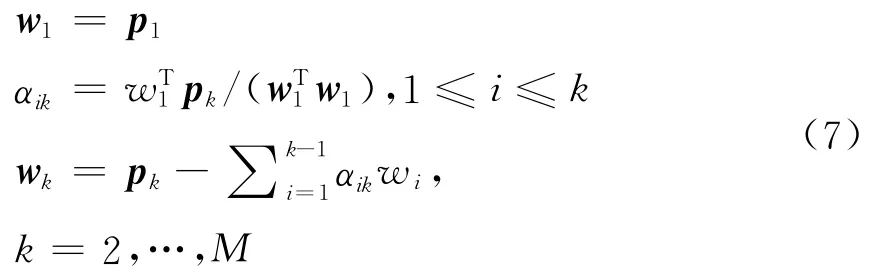
与一般的LS方法相比,OLS方法具有一些优越的数值性质.在实践中,备选的输入变量点x(t)的数量一般很庞大,输入变量应选作数据集的一个子集;也就是说,可选用的回归算子个数M可以很大,而我们可能只需Ms(Ms≪M)个重要的回归算子就可以得到性能令人满意的模型了.下面介绍的一种前传回归方式的OLS算法就是来选择这些重要回归算子的,对于i=j,wi和wj正交,y(t)的能量为

2 OLS在风电机组齿轮箱输入变量选择上的应用
在风电机组齿轮箱温度预测的建模中,所使用的数据为SCADA系统中的监测数据,SCADA系统,即风电机组数据采集与监视控制系统,它是近几年应用于风电机组的状态监测系统,其主要功能为定期采集并记录风电机组各部件或子系统的状态数据,每10min记录一次机组的参数,所记录的参数多达几十种.在风电机组齿轮箱的温度预测中的输入变量就需要在该数据库中选择出来.
将SCADA系统中所有M个监测数据组合成OLS算法回归算子集合P,那么在风电机组数据采集与监视控制系统中选择出合适的齿轮箱温度预测输入变量的问题,可以看成在拥有M个回归算子的集合P中选出有限个算子Ms的问题.这样便可以依照上节将OLS法应用于风电机组齿轮箱输入变量选择.
运用SCADA系统中的监测数据,OLS法选择齿轮箱温度预测输入变量的具体过程为
①在SCADA系统中确定所有的备选输入变量集,针对要学习的目标形成一组包含期望输出变量及所有备选输入变量的样本集.
② 确定容差ρ和输入变量初始个数Ms.由所有备选输入变量形成回归算子矩阵P.
③用OLS法选择Ms个最显著的回归算子,具体步骤参见上节.
④检查压缩比是否满足容差ρ,若满足则停止计算,转步骤⑤;否则,Ms=Ms+1,转步骤③,继续选择回归算子.
⑤得到Ms个回归算子即选出的输入变量.
3 OLS法与相关系数法在齿轮箱输入变量选择上的比较
以甘肃省某风电场的一台机组在2013年2月的SCADA运行数据为基础,进行OLS法与相关系数法在齿轮箱温度预测输入变量选择的比较.从SCADA众多监测参数中初选出备选输入变量集,最终选择出29个备选的输入变量.选择2013年2月5、6日两个典型日的数据作为研究对象.
3.1 相关系数法选择输入变量
相关系数法的计算公式为
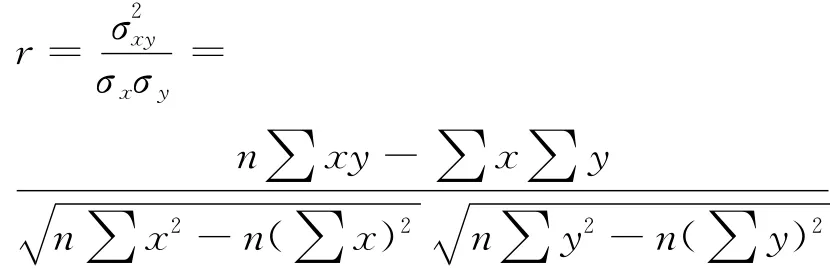
计算SCADA系统中29个输入变量与输出变量即齿轮箱油温相关系数,部分相关系数见表1.
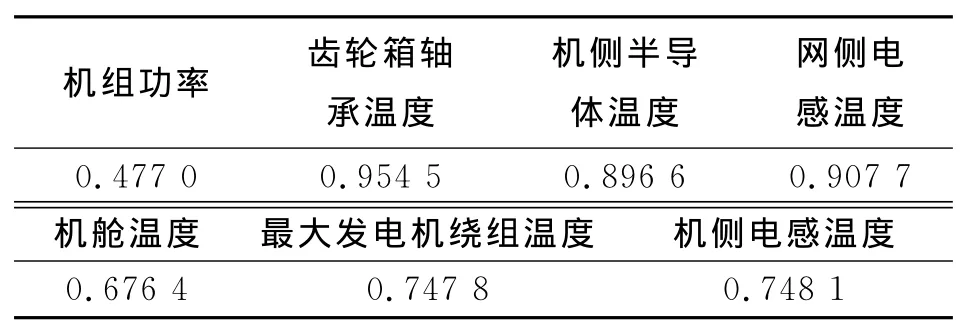
表1 齿轮箱温度与部分相关变量的相关系数Tab.1 Correlation coefficient between gearbox temperature and other variables
表1中选择相关系数最大的若干个神经网络变量作为神经网络的输入,选择结果为:齿轮箱轴承温度(0.954 5)、网侧电感温度(0.907 7)、机侧半导体温度(0.896 6)、网测半导体温度(0.887 9)
3.2 OLS法选择输入变量
设初始输入变量数Ms=4,容差ρ=0.000 1,OLS选择输入变量结果见表2.

表2 OLS法输入变量选择结果Tab.2 OLS method using input variable selection
3.3 算例分析
为比较两种输入变量选择方法对齿轮箱温度预测精度的影响,选择甘肃某风电场2月5日正常运行的144个监测数据点作为神经网络训练数据,2月6日的144个数据点作为神经网络测试数据,在相同的训练集和测试集的基础上,运用相同的神经网络来学习和比较2种方法的结果.在这里选择BP神经网络,训练的最大迭代次数为100次,训练目标为0.000 04,OLS法神经网络的输入为表2中四个输入变量,相关系数法神经网络的输入为表1中的四个输入变量.OLS法选出的输入变量进行预测的效果与相关系数法选出的输入变量预测效果对比图如图1所示.
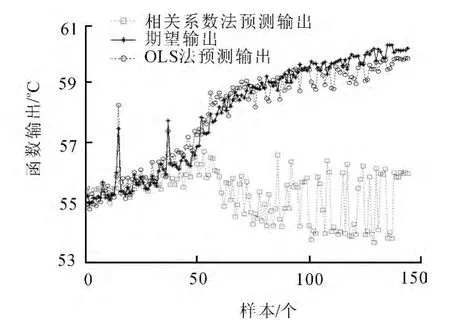
图1 OLS法与相关系数法的输入变量预测效果对比图Fig.1 Prediction between OLS and Correlation Coefficient
从图1的对比中知道,二者的预测效果有着明显的区别.
两种方法预测的误差对比图如图2所示.
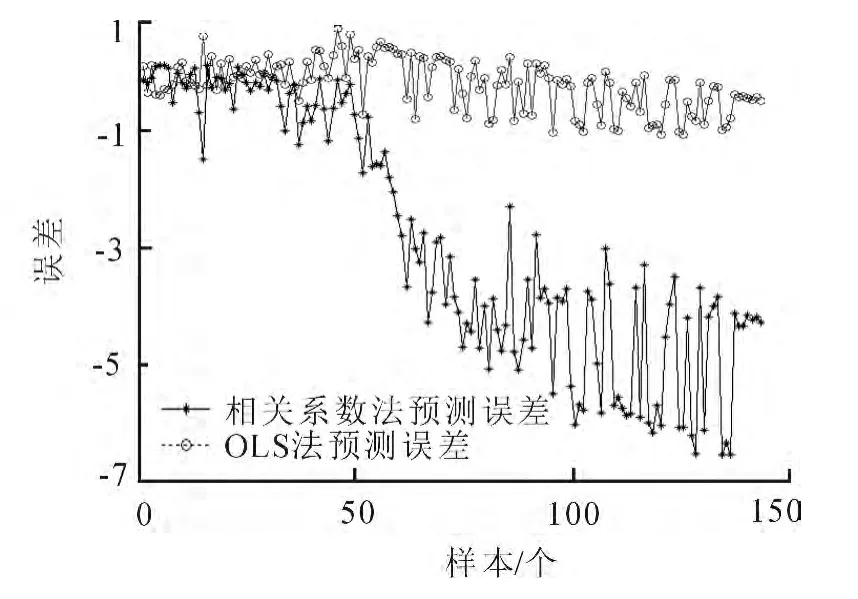
图2 两种方法预测的误差对比图Fig.2 Error between two methods
从图2的对比中知道,二者的预测效果有着明显的区别.此外,本文还选取了均方误差(MSE)、均方根误差(RMSE)和平均绝对百分比误差(MAPE)来作为预测结果的评价指标.每种方法连续运行十次取三种误差的平均值,两种方法预测的精度见表3.

表3 OLS法与相关系数法预测精度对比图Tab.3 Prediction accuracy between OLS and Correlation Coefficient
从表3看出,在输入变量、隐含层节点数、训练次数全都相同的条件下,OLS法选择出来的输入变量精度明显好于相关系数法选择出来的变量,验证了OLS法选择风电机组齿轮箱温度预测输入变量的有效性.
从表3看出,在输入变量、隐含层节点数、训练次数全都相同的条件下,OLS法选择出来的输入变量精度明显好于相关系数法选择出来的变量,验证了OLS法选择风电机组齿轮箱温度预测输入变量的有效性.
4 结 论
本文提出了正交最小二乘法用于风电机组齿轮箱温度预测输入变量的选择,通过正交最小二乘法与相关系数法仿真结果的对比,证实了正交最小二乘法的仿真结果优于相关系数法,验证了正交最小二乘法用于风电机组齿轮箱温度预测输入变量选择的有效性.最小正交二乘法在选择输入变量的过程中也存在着无法准确解释输入变量各负荷间的变化关系的缺点,建立输入变量各负荷间的变化关系,是正交最小二乘法用于输入变量选择今后需要解决的问题.
[1] KIM K,PARTHASARATHY G,ULUYOL O,et al.Use of SCADA Data for Failure Detection in Wind Turbines [C ]//Proceedings of 2011Energy Sustainbility Conference an Fuel Cell Conference,Washington,2011:7.
[2] MESQUITA BRANDAO R F,J.A.Beleza Carvalho.Forecast of Faults in a Wind Turbine[J].IEEE Conference Publications,2012:170.
[3] ZAHER A,MCARHTUR S D J,INFIELD D G.Onlion Wind Turbine Fault Detection through Automated SCADA Data Analysis[J].Wind Energy,2009,12:574.
[4] 郭鹏,David Infield,杨锡运.风电机组齿轮箱温度趋势状态监测及分析方法[J].中国电机工程学报,2011,31(32):129.GUO Peng,David Infield,YAng Xi-Yun.Wind Turbine Gearbox Condition Monitoring Using Temperature Trend Analysis[J].Proceedings of the CSEE,2011,31(32):129.(in Chinese)
[5] 吉小军,李世中,李霆.相关分析在特征选择中的应用[J].华北工学院测试技术学报,2001,15(1):15.JI Xiao-Jun,LI Shi-zhong,LI Ting.Application of the Correlation Analysis [J].Journal of Test and Measurement Technology,2001,15(1):15.(in Chinese)
[6] DREZGA I,RAHMAN S.Input Variable Selection for ANN-Based Short-Term Load Forecasting[J].IEEE Transactions on Power Systems,1998,13(4):1238.
[7] 闫闯.多元回归模型中变量选择问题研究[D].哈尔滨:黑龙江大学,2011.YAN Chuang.Variables in a Multiple Regression Model Selection Study[D].Harbin:Heilongjiang University,2011.(in Chinese)
[8] 高山,单渊达.神经网络短期负荷预测变量选择新方法[J].电力系统自动化,2001,25(22):1.GAO Shan,SHAN Yuan-da.Novel Input Variable Selection for Ann Short-Term Load Forecasting[J].Automation of Electric Power Systems,2001,25(22):1.(in Chinese)
[9] CHEN S,COWAN C F N,GRANT P M.Orthogonal Least Squares Learning Algorithm for Radial Basis Functions Networks[J].IEEE Trans On Neural Net-Works,1991,2(2):302.
[10] MASTOROCOSTAS P A,THE OCHARIS J B,BAKIRTZIS A G.Fuzzy Modeling for Short Term Load Forecasting Using the Orthogonal Least Squares Method[J].IEEE Trans On Power Systems,1999,14(1):29.(in Chinese)
[11] 徐秉锋,张百灵,韦岗.神经网络理论与应用[M].广州:华南理工大学出版社,1994.XU Bing-feng,ZHANG Bai-ling,WEI Gang.Artificial Neural Network and Its Application[M].Guangzhou:South China University of Technology Press,1994.(in Chinese)

