半潜式浮基风电平台设计及波浪动力响应分析

石陆丰，程建生，段金辉，隋元松

（解放军理工大学野战工程学院，南京 210007）

0 引 言

近年来随着能源枯竭问题的日益严峻，海上风能的开发受到重视，并已逐渐由浅海向深海发展。浮基风电平台是深海风电机组的基础结构。由于浮基风电系统重心高，受到风、浪、流及冰荷载等的影响，受力情况复杂，使得浮基风电平台的设计面临很多技术上挑战和理论应用的难点。目前研究较多的浮基风电平台主要有 Spar结构基础[1]、张力腿结构基础( tension leg platform，TLP)[2,3]、半潜式结构基础和浮筒( 或驳船) 基础。

半潜式浮基风电平台由于具有水深适用范围广、安装工作量少、总成本低等优点，受到了各国研究人员的广泛关注。Zambrano T[4]等人开发了一种支撑3个风力机的半潜式平台MiniFloat，采用基于墨西哥的暴风模型傅里叶谱进行了深海风电浮式基础结构的运动响应分析，通过采用龙格-库塔法得到了平台结构在六个自由度上的响应，并求解出作用在结构上的风浪荷载和锚链承受力。而后美国又开发了单风力机半潜式平台WindFloat[5～7]，并针对平台的流体和结构动力特性分别展开了研究。Thomas Zambrano等人[8]基于Wamit软件平台计算作用在多风机半潜平台上的波浪力，并分析了波浪作用下半潜平台的六个自由度运动响应。唐友刚[9]针对所设计的水深为60m的600kW水平轴半潜式海上风力发电机，使用有限元法建立了包括风机、塔架、浮式基础和系泊系统的数学模型，对波浪载荷作用下的浮式基础动力响应进行了频域分析。研究发现，平台的运动会导致风力机功率的波动，引起电力输出的不稳定[10]。因此，在海上浮式风力机的设计中，平台的运动特性应作为主导因素考虑。

为了提升半潜式浮基平台的稳性，采用悬挂压载物降低平台重心的方法设计了一种半潜式浮基风电平台，并应用ADINA软件，基于CFD方法，采用边界造波法、ALE动网格技术以及网格变疏增大数值黏性的消波法构建了数值波浪水池，对平台在波浪中的运动进行数值模拟。

1 浮基风电平台概念化设计

受风电机组的影响，深海浮式基础系统较普通石油钻井平台而言倾覆力矩较大，为了保证风机发电的稳定和整个系统部件免受疲劳损伤，设计在平台的下部悬挂大重量的压载物来降低整个系统的重心以抑制整个平台在各种荷载作用下的晃动。此压载物设计总质量 2400t，体积 1000m3，尺寸为 10m×10m×10m的立方体，材料为防腐钢筋混凝土。浮基风电平台概念化设计见图1、2，设计的主要参数见表1。

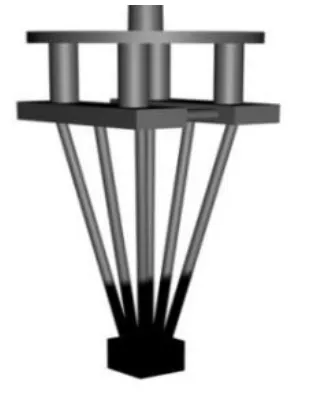
图1 深海浮基风电平台概念化设计

图2 深海浮基风电平台模型

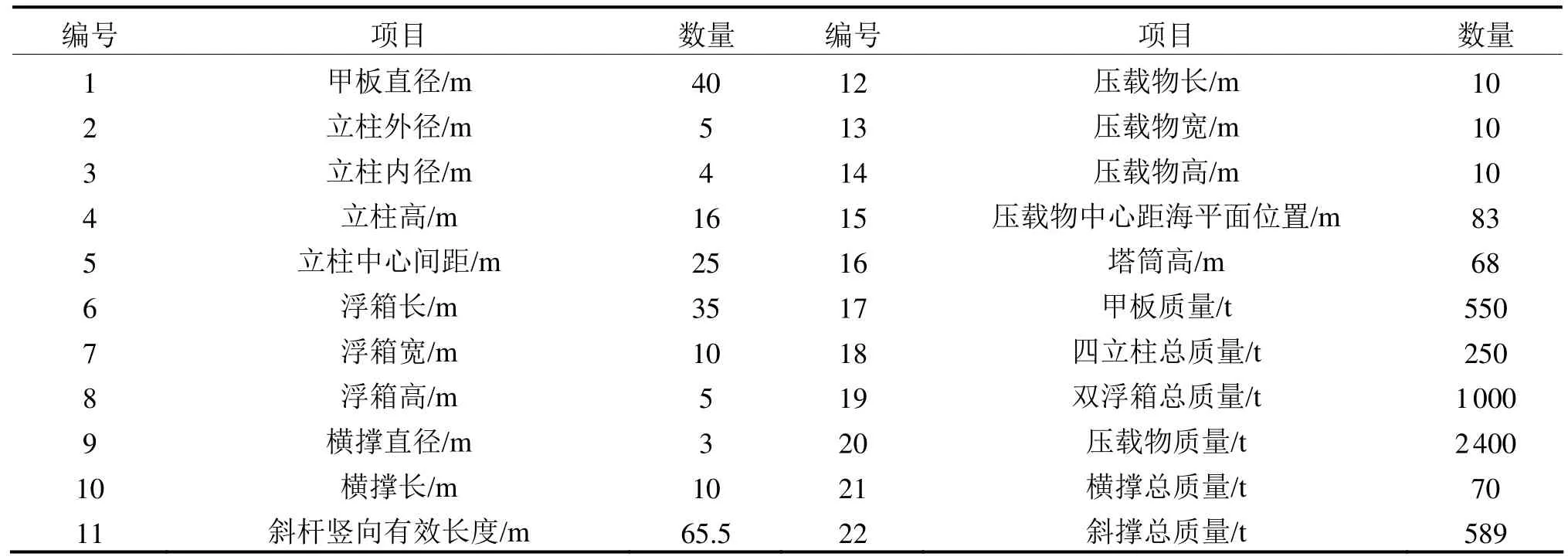
表1 浮基风电平台概念化设计的主要参数

2 波浪水池的数学模型

2.1 流体模型

流体控制方程用非定常不可压缩雷诺平均 Navier-Stokes（RANS）方程求解。为了跟踪固体边界和流体边界的运动状况，很好地反映耦合界面的网格变化，采用任意拉格朗日-欧拉（Arbitrary Lagrangian-Eulerian description）坐标系。ALE描述下的连续性方程和动量方程为：

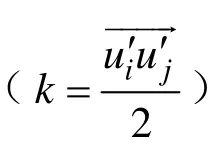
2.2 造波与消波

采用线性波数值造波方法实现造波。线性波理论是最常用的波浪理论之一，其表达形式简单，使用方便，线性波主要用于小振幅波。计算中采用自由面位移的理论公式为：

波浪水质点在各方向的速度为：

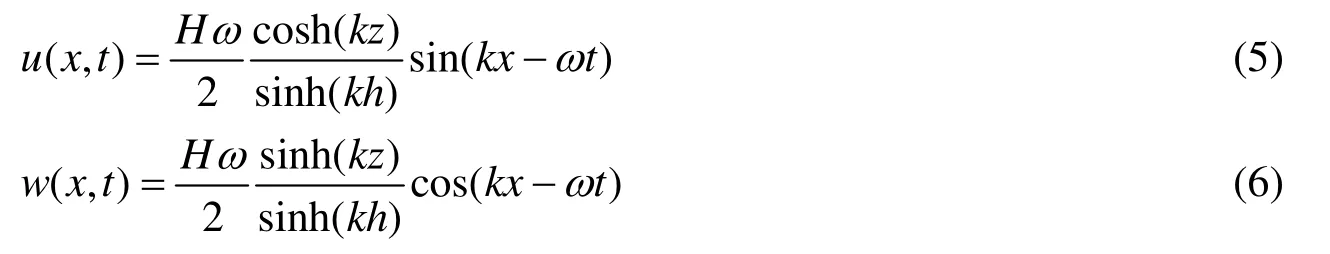
色散关系为：

式中：H——波高，h——静水深，λ——波长，k=2π/λ——波数，g——重力加速度，ω=2π/T——圆频率，T——波浪周期，c——波速。依据上述公式可知，给定模拟波浪的周期、波高和静水深，便可以得到入射边界上边界点的速度值，将其赋予边界进行造波。

利用ADINA软件建立计算所用的三维几何模型，入射波波高H=6m，波长λ=100m ，水深h=200m，根据色散关系式（7）求得波浪周期T=6s，同时，λ/2＜h＜∞，属于深水波。通过对数值水池某时刻的波形和某位置的波幅历时时程进行监控。图3所示为采用本文数值方法所造波在t=48s时刻波面变形的三维形态。在距离入口100m、200m处设置了两个观测点进行波面的历时时程监控，两监测点波面历时时程数值解与解析解对比（见图4）。从图4可知，所构建的三维波浪数值模型波面的数值解和理论解吻合很好。消波区采用网格变疏增大黏性的数值黏性消波方法，即对消波区段人为地定义较大的黏性来增大消波区域段的阻尼，达到消波的目的。

图3 t=48s时刻线性波三维波面

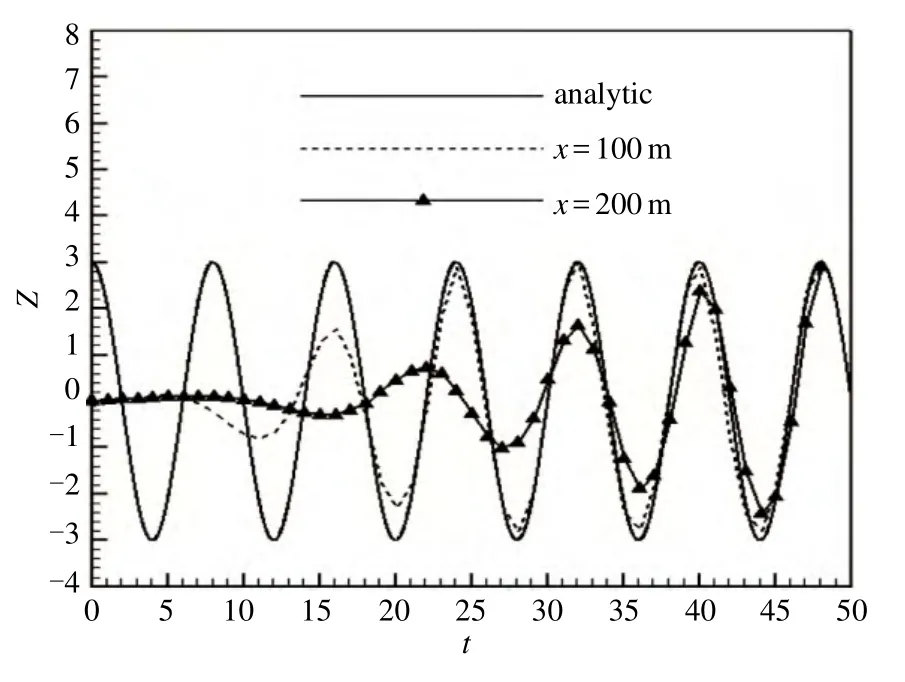
图4 100m、200m监测点处波面历时曲线对比

2.3 浮基风电平台运动与流体的耦合

浮基风电平台的六个自由度控制方程表达式如下：

式中：下标c——浮基风电平台的转动中心，m——平台的质量，——速度矢量，Ic——惯性矩张量，——角速度矢量，和——作用在平台上的力和力矩矢量。

当作用在平台上的力和力矩已知时，其运动的速度、角速度及位置、姿态等可以通过式（8）、（9）求解积分得到。

3 数值模型验证

采用 ADINA软件进行数值波浪水池的构建及验证和深海风电浮式基础在波浪作用下的运动响应研究。依据第20届ITTC半潜平台原型1:70的尺寸建立了数值计算模型，进行波浪作用下三维模型的数值模拟，并将计算结果通过分析整理，与模型试验结果比较，以验证构建的数值波浪水池的可靠性。模型结构见图5。

数值波浪水池计算区域范围为1000m×400m×200m，浮体位于区域中间，吃水深度为24m，计算区域分3部分，波浪生成区长400m，工作区长200m，消波区长400m，见图6。

采用四面体网格，整个流固耦合区域网格总数（包括流体和固体）为509586个，计算区域网格划分情况见图7。

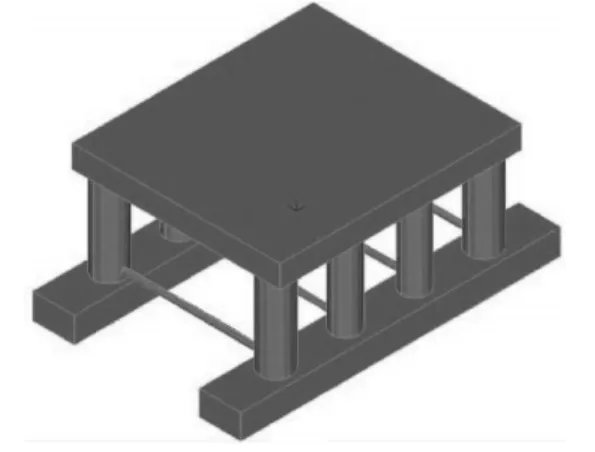
图5 ITTC半潜平台数值模型

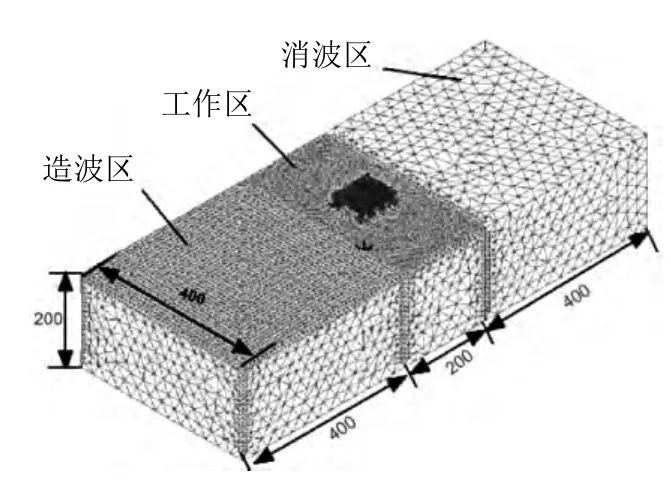
图6 ITTC平台模型分析区域

图7 计算区域网格划分

水池左侧为入射边界，波浪水池侧壁和水池底部结构边界条件都设置为固壁边界，与半潜平台接触的流体表面定义为FSI边界(即流固耦合边界)，而自由表面边界设置在整个流体模型的上表面处。

初始条件：风电浮式基础平台静止，不受外力的作用；压力设为静水压；时间步长取为波浪周期的1/200。针对下述波浪环境条件，将ADINA软件计算得到的数值模拟计算结果与在哈尔滨工程大学深水池所做试验的结果进行对比（见图8，表2）：

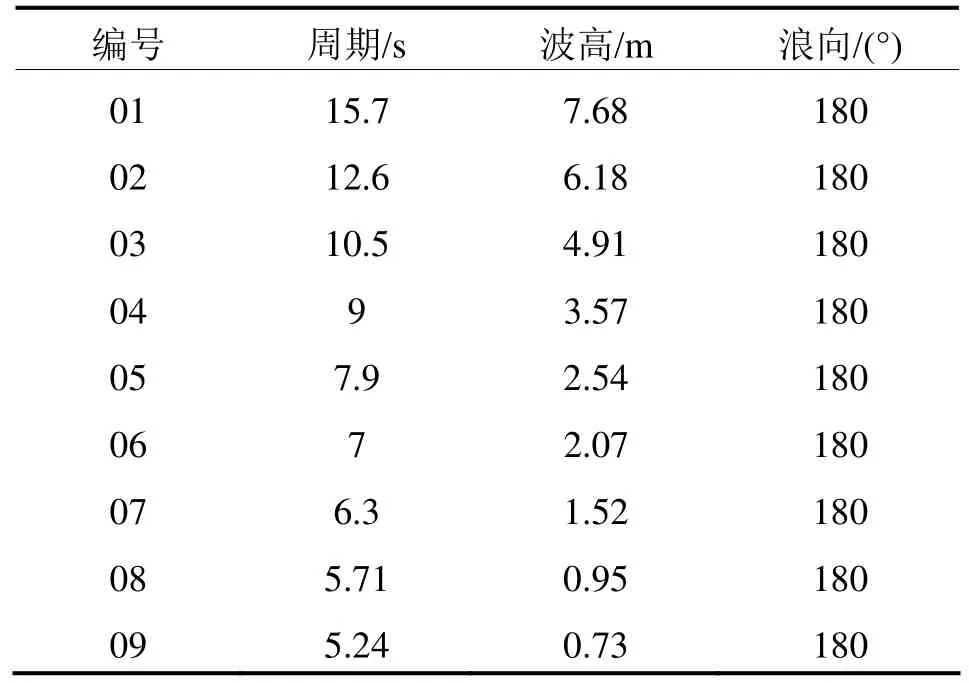
表2 规则波作用下的数值模拟工况

图8 ITTC半潜平台试验模型

从图9可见，ITTC试验平台的首摇响应试验值与计算值有较大差异，这是因为理论分析时，浪向是不会改变的，但模型试验时，由于ITTC试验平台的艏摇，实际浪向和波浪力也发生了改变，试验结果必然会与理论分析结果有所差异。但总体来说，平台各自由度 RAO通过数值计算所得的结果与试验结果变化规律基本相似，吻合程度达到一定的要求，从而证明了构建的三维数值波浪水池是可靠的，数值计算所采用的计算方法能够很好地模拟规则波作用下平台的运动状态。

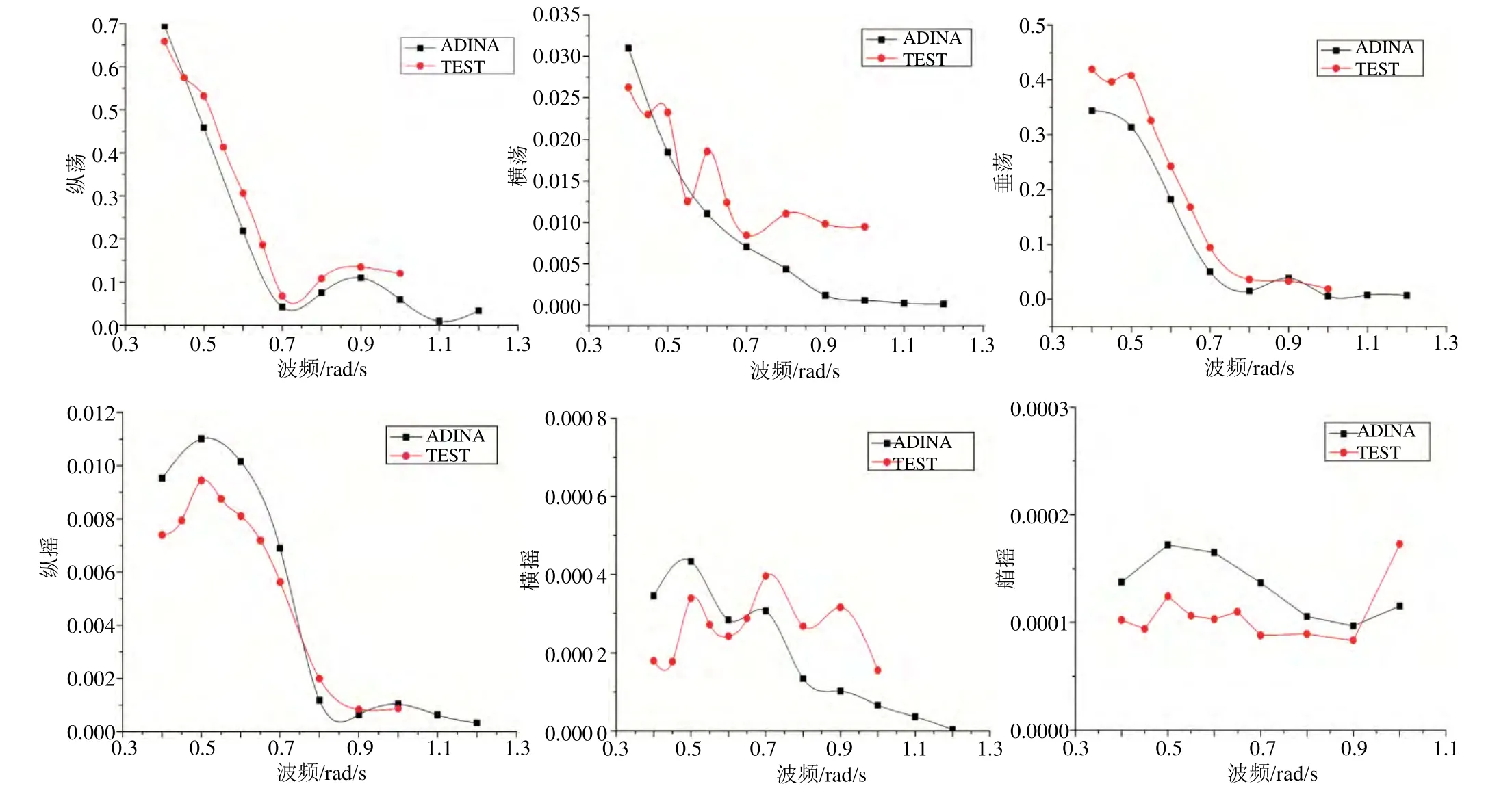
图9 浪向角180°时计算结果与试验结果对比

4 水动力响应分析

利用上述方法建立的数值波浪水池对概念设计的半潜式浮基风电平台在波浪作用下的动力响应进行数值模拟研究，从波高、波浪周期两方面对浮基平台进行动力响应分析。

4.1 模型建立

首先建立计算所需的几何模型，对结构进行网格划分，均采用四面体网格，除6根连接压载物的杆件网格尺寸为0.5m外，其余结构网格长度均取为1.0m，输出的整体结构有限元模型见图10。其中节点数为36516个，单元数为155681个。

4.2 计算区域及网格划分

计算区域大小取为600m×200m×200m，即是三维波浪水池的3部分尺寸为波浪生成区、工作区和消波区，其长度分别为150m、150m和300m，浮体距入口200m处，水深为200m。

在造波区和工作区，x方向网格长度取为2m，y方向网格长度取为4m，Z方向为5m，底边为20m，消波区表面网格X向为10m，Z向为10m，其中工作区中流固耦合界面网格尺寸为0.5m，连杆部分为0.25m。整个流固耦合计算模型网格点数为109427点，单元数为624021个，计算区域网格划分情况见图11。

4.3 不同波浪周期情况下浮式基础横摇、纵摇运动分析

分别对波高5m，波浪周期分别为4s、6s和10s，对应波长分别为25m、56m和156m时的浮基风电平台进行动力响应分析。横摇响应时程曲线见图12，纵摇响应曲线见图13。

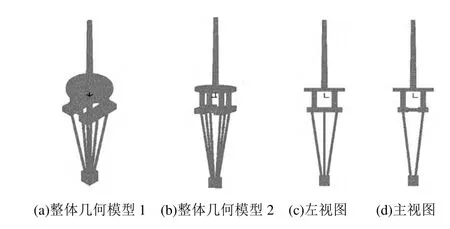
图10 风电浮基整体结构有限元模型

图11 流固耦合分析中流体模块

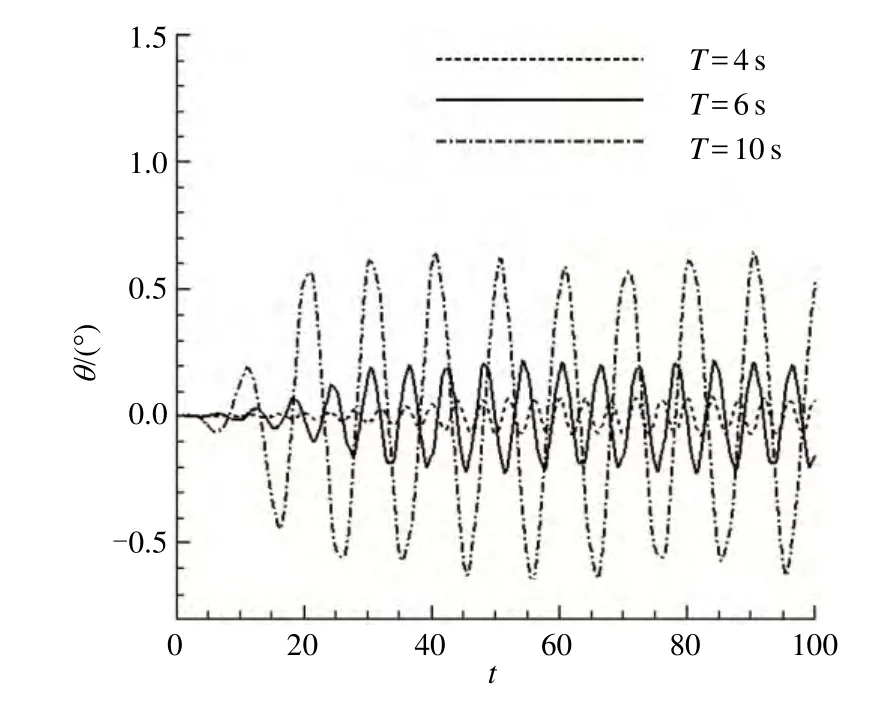
图12 不同波浪周期时横摇响应时程曲线

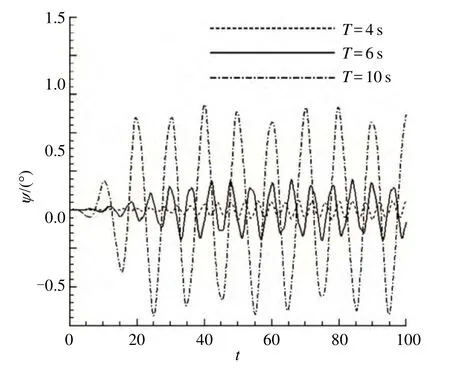
图13 不同波浪周期时的纵摇响应时程曲线

由图12、13可知，波浪周期为4s时，浮式基础的纵摇角度很小，在所选时间段内，最大纵摇角峰值达到 0.5°，而横摇角更小，最大横摇角达到 0.1°；波浪周期为 6s时，浮式基础的纵摇角度比波浪周期为4s时的纵摇角度稍有增加，在所选时间段内，最大纵摇角达到1.6°，而横摇角表现出相同的增大规律，最大横摇角度达到0.21°；波浪周期为10s时，浮式基础的纵摇增加幅度相比于4s情况较大些，在所选时间段内，最大纵摇角度达到5.4°，横摇角变化增加幅度不大，最大横摇角度达到0.65°。

4.4 不同波高情况下浮式基础横摇、纵摇运动分析

取波浪周期为10s，浪高分别为3m、5m和7m的风电浮基进行动力响应分析，通过数值模拟得到3种浪高情况下风电浮基的横摇、纵摇响应时程曲线，见图14、15。

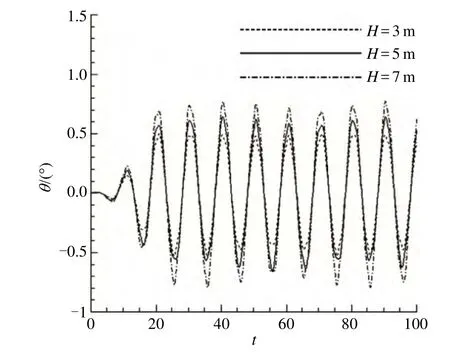
图14 不同波高时的横摇响应时程曲线

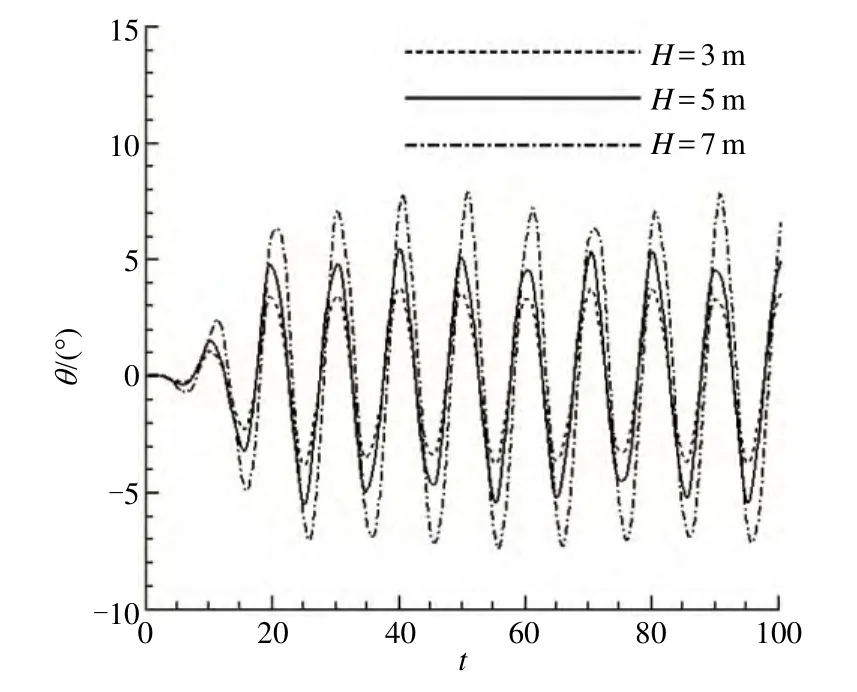
图15 不同波高时的纵摇响应时程曲线

从图 14、15中浮基风电平台横摇、纵摇响应时程曲线中可知，浮基的横摇、纵摇角度整体上随波高的增大而增大，并且波高3m时风电浮基最大纵摇角度达到3.8°，波高5m时浮基纵摇角度如上述为5.4°，波高为7m时浮基的纵摇角度达到7.8°，3m、5m和7m波高情况下浮基横摇角度峰值分别为0.52°、0.65°和 0.79°。

5 结 语

利用悬挂压载物降低平台重心的方法设计了一种半潜式浮基风电平台，并基于CFD方法，应用ADINA软件建立了数值波浪水池，对第20届ITTC半潜平台在规则波作用下的动力响应进行数值模拟，模拟结果与试验值吻合较好，验证了所构建的三维数值波浪水池的可靠性。

利用构建的数值波浪水池对新设计的半潜式浮基风电平台在规则波作用下的运动进行数值模拟，给出了浮基风电平台在不同波高、波浪周期情况下横摇、纵摇时程曲线。通过数值计算结果分析，得出结论：在所选海况下，所设计的半潜式浮基风电平台的纵摇角最大值为7.8°，略超出单个风机系统在正常作业情况下所要求的系统俯仰角运动范围（国外著名学者Thomas Zambrano等人[11]提出在正常作业情况下，深海风电场单个风机系统的平均俯仰角应在±6°范围内，而动态俯仰角在±15°范围内）。本数值计算结果将有助于了解浮基风电平台塔架顶端的运动、位移和受力，为海上风机系统的优化设计提供合理的荷载参数。

[1] 杨雄文，樊洪海. Spar平台结构型式及总体性能分析[J]. 石油矿场机械，2008，37(5): 32-35.

[2] 杨雄文，樊洪海. TLP平台结构型式及总体性能分析[J]. 石油机械，2008，36(5): 70-73.

[3] 徐万海，曾晓辉，吴应湘，等. 深水张力腿平台与系泊系统的耦合动力响应[J]. 振动与冲击，2009, 28(2): 145-150.

[4] Zambrano T, Mac Cready T, Kiceniuk T, Jr, et al. Dynamic Modeling of Deepwater Offshore Wind Turbine Structures in Gulf of Mexico Storm Conditions[A]. 25th International Conference on Offshore Mechanics and Arctic Engineering[C], Hamburg,2006. 1-6.

[5] Bye A, Erbrich C, Rognlien B, et al Geotechnical Design of Bucket Foundations[A]. Offshore Technology Conference[C],Houston, 1995.

[6] Rasmussen J L, Feld T, S rensen P H. Bucket Foundation for Offshore Wind Farms Comparison of Simplified Model and FE Calculations[A]. OWEMES 2000[C], Sicilia, 2000.

[7] Feld T. Design Procedures for Bucket Foundations—A New Innovative Foundation Concept Applied to Offshore Wind Turbines[A]. Offshore Wind Energy Conference[C], Brussels, 2001.

[8] Thomas Zambrano, Tyler MacCready and Taras Kiceniuk Jr. et al. Dynamic Modeling of Deepwater Offshore Wind Turbine Structures in Gulf of Mexico storm condition[A]. Proceedings of OMAE 2006 25th International Conference on Offshore Mechanics and Arctic Engineering[C]. Hamburg, ASME, 2006: OMAE2006-92029.

[9] Tang Yougang, Hu Jun, Liu Liqin. Study on the Dynamic Response for Floating Foundation of Offshore Wind Turbine[A]. The ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering[C], Rotterdam, 2011, 19-24.

[10] 叶小嵘，张 亮，吴海涛，等. 平台运动对海上浮式风机的气动性能影响研究[J]. 华中科技大学学报：自然科学版，2012,40(3): 123-126.

[11] J.M. Jonkman, M.L. Buhl Jr. Development and Verification of a Fully Coupled Simulator for Offshore Wind Turbines[A]. The 45th AIAA Aerospace Science Meeting and Exhibit, Wind Energy Symposium[C]. Nevada, 2007: NREL/CP-500-40979.