焊接模型的非线性方程组参数估计法❋

霍 平，张海旺，李宁宁，张光浩，张学锋

（1.河北联合大学 机械工程学院，河北 唐山 063009；2.唐山开元自动焊接装备有限公司，河北 唐山 063020）

0 引言

在以CCD相机为传感器的机器视觉焊接系统中，往往需要对系统进行标定，以确定世界坐标系和图像坐标系的关系，这样就可以通过图像的尺寸信息导出焊缝实际尺寸信息。目前研究的透视变换矩阵模型一般都基于小孔成像原理，利用矩阵变换，导出三维空间坐标系和二维图像坐标系的关系，且其数学模型一般均为非线性方程。由于方程中参数的个数大于独立方程的个数，而且方程中参数不是相互独立的，所以出现了过参数化现象。本文运用非线性方程组参数估计法对其进行了研究，以解决焊接模型标定过程中的过参数化问题。

1 利用透视变换矩阵建立的焊接模型

基于小孔成像的基本原理和一系列的矩阵变换，建立如图1所示的焊接数学模型［1］。数学模型标定的实质是推导出世界坐标系和图像坐标系的几何对应关系。首先应建立世界坐标系（Xg，Yg，Zg）和物体成像的图像坐标系（Xi，Yi，Zi），世界坐标系和图像坐标系都为左手坐标系，Oc为图像坐标系的中心，Og为世界坐标系的中心。P为线结构光的平面，Zi轴斜向下，与光平面P相交于Og点。世界坐标系Zg轴在光平面P内，且在图像坐标系Zi轴与Xi轴所决定的平面内，方向朝上。由左手坐标系确定Xg轴。Yg轴平行于Yi轴，其目的是减少系统标定的参数，简化模型。

由透视变换矩阵的数学模型可以得出：

其中：Vi为物体在世界坐标系中的坐标；Vo为物体在图像中的坐标；H为总的变换矩阵，具体表达式见参考文献［1］。

图1 焊接数学模型

但是在实际应用中我们要解决的是由图像坐标求解出世界坐标。设H－1为H的逆矩阵，则有：

其中：f为透镜中心到像平面的距离；β为Zi轴和光平面P的夹角；Dpc为像面中心到光平面的垂直距离；Dgp为Op到图像坐标系的水平距离，如图1所示。

2 传统的焊接系统标定过程

焊接模型的方程可以表示为：其中：u和v为图像像素坐标系中的坐标；M1为摄像机的内部参数矩阵；M2为摄像机的外部参数矩阵；mij为M1和M2相乘后的系数矩阵。

焊接系统的标定其实就是对式（1）和式（3）的未知参数进行求解。由于未知数个数大于有效的方程个数，故各参数之间并不是相互独立的，为了能够求解出方程，就必须找出至少6个独立的数据点。

消去Zi即可得到如下方程组：

式（4）可简写为：

其中：m为摄像机内部参数和外部参数相乘后的系数矩阵；U为常系数矩阵；K为已知的标定点参数。式（5）的最小二乘法解为m＝（KTK）－1KTU。求解了m矩阵就可以求得内部参数矩阵M1和外部参数矩阵M2，进而就可以求得模型的各参数数值。

3 焊接模型的非线性方程组参数估计法

一般地，设L为求解目标函数，X＝［Xg1，Xg2，…，Xgn］T为未知参数矩阵，Δ为误差向量，则非线性方程组可写为［4］：

设参数X的估计值为Xo，则求解非线性模型的估计值就是求参数X的估计值Xo，使：

由于f（Xo）是Xo的非线性函数，因此无法对式（6）求导，只能寻找近似解使X＊满足如下关系式：

其中：R（X＊）为近似的目标函数；R（Xo）为待求的目标函数。

利用泰勒公式在Xk附近展开，去二项得：

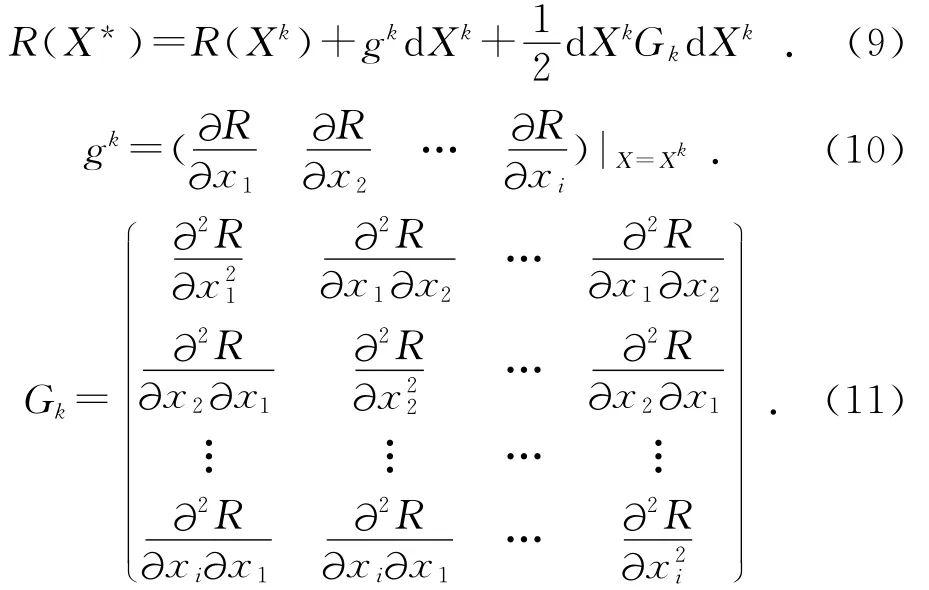
其中：dXk＝X＊－Xk。由此可以得到迭代公式：

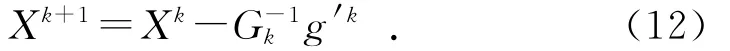
可以根据最小二乘法求解的数值作为X的初始值，代入式（12）进行求解。本方法对于简单模型求解方便，而对于复杂模型的求解，可根据如图2所示的计算非线性方程组参数的程序流程进行求解。

4 实验结果及分析

本文需要标定的设备如图3所示。

本文所提出的实验，选取的数学模型较为简单，以方便验证两种不同的理论方法。选取的参数如下：摄像机的镜头焦距为12mm，β为15°，Dgp为70mm。本实验的标定值均为多次标定的平均值。标定结果见表1。

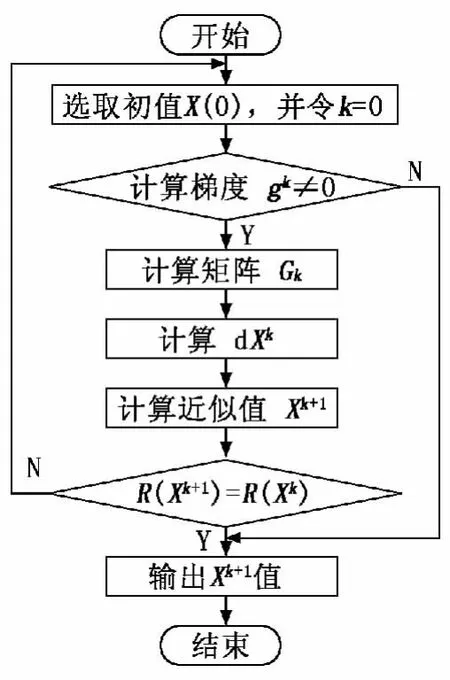
图2 计算非线性方程组参数的程序流程图

图3 需要标定的设备

表1 标定结果

本实验主要采用了传统标定法和非线性方程组法标定两种方法，分别在有干扰和无干扰的情况下进行。由于电弧干扰的存在，导致标定板上特征点的提取不准确，从而影响标定参数的准确性。对比表1中的标定值，当实验有电弧干扰和没有电弧干扰时，实验的结果误差较大，电弧的干扰很强。即使在新方法中，电弧的干扰也是不可去除的，因为新方法的初值依赖于传统方法的计算结果。新方法的计算精度还取决于程序中的迭代次数，由于计算的实时要求，所以迭代次数不可能很大，因此限制了计算的精度，但是从实验数据上还是可以分析出新的计算方法要优于传统的标定方法。

5 结束语

本文在透视变换矩阵焊接模型基础上，介绍了标定过程中的关键步骤。对焊接模型参数运用传统的最小二乘法进行了参数估计。针对传统标定的过参数化问题，提出了焊接模型的非线性方程组参数估计法，对焊接模型的参数进行了重新估计。通过实验证明非线性方程组参数估计法在求解焊接模型参数时还是很有效的。

［1］ 贺忠海，王宝光.线结构光传感器的模型及成像公式［J］.光学精密工程，2001，6（3）：270－273.

［2］ 姜勇.摄像机标定算法库的设计与实验验证［D］.青岛：青岛大学：2006：36－40.

［3］ 张国亮，赵彦玲，王一文，等.焊缝视觉跟踪系统中标定算法的研究［J］.哈尔滨理工大学学报，2005（1）：27－31.

［4］ 王新洲.非线性模型参数估计理论与应用［M］.武汉：武汉大学出版社，2002.