单自由度八连杆机构链型的拓扑特性研究

杨 益，宋爱平，郭 伟，陶建明

（扬州大学 机械工程学院，江苏 扬州 225009）

0 引言

八杆机构的链型数目较多，所以在机构分析时对链型的选择比较困难，为此研究和掌握基本链型的拓扑特性就显得非常重要。机构链型的拓扑特性仅与构件和运动副数目及其连接情况有关，而不涉及构件尺寸和运动副的相互位置。因此，拓扑特性并不等于实际机构的特性，但它却反映了运动链的固有属性［1，2］。本文对单自由度八杆机构链型的机械利益、紧凑性、刚性和动态灵敏度等拓扑特性进行了比较深入的研究。

1 机械利益

机械系统的输出力与输入力的比值反映了系统传递力的性能，因此把这个比值定义为机械系统的机械利益。假设在理想的机械系统中输入功与输出功相等，即：

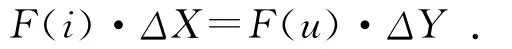
其中：F（i），F（u）分别为输入力和输出力；ΔX，ΔY分别为输入位移和输出位移。则机械利益M为：

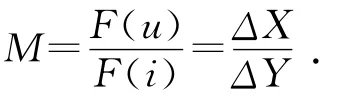
根据M的表达式可知，输入、输出之间为非线性关系的运动链，可以用较小的输出位移以及较大的输入位移和较小的输入力来获得理想的机械利益，得到较大的输出力。获得较高的机械利益跟运动链的非线性运动潜力有关，潜力越大得到的机械利益也就越高。

连杆机构中最常见的是四杆机构，在四杆的基础上增加一杆即变为五杆机构，依此类推得到六杆、七杆以及八杆机构等等。所以八杆机构是在四杆机构上增加杆件得到的。为更好地研究八杆机构的机械利益，先了解四杆、五杆和六杆链型机构的机械力益。

图1为四杆、五杆、六杆链型。图1（a）为四杆链型（自由度为1），以杆1为机架，杆2为输入，杆4为输出，θ2为输入角位移，θ4为输出角位移，θ4＝f（θ2，l2，l3，l4）。图1（b）为五杆链型（自由度为2），以杆1为机架，杆2和杆5为输入，杆4为输出时，θ2和θ5为输入角位移，θ4为输出角位移，θ4＝f（θ2，θ5，l2，l3，l4，l5）。图1（c）为六杆链型（自由度为1），以杆1为支架，杆2为输入，杆6为输出，θ2为输入角位移，θ6为输出角位移，θ6＝f（θ2，l2，l3，l4，l5，l6）。根据得到的参数表达式发现六杆基本链型和五杆基本链型都有6个自变量参数，那么产生的非线性的潜力相当，并且可以看出六杆、五杆基本链型的非线性潜力比四杆基本链型的更大。

图1 四杆、五杆、六杆链型

根据颜氏创造性机构设计［3］可以得到16种单自由度八连杆链型，从中选取的10种单自由度八杆机构链型如图2～图4所示。从以上机械利益的理论可判断出图2（d）机构链型（含有3个五杆闭环）非线性运动的潜力相对较高，也就是其机械利益最大；图2（b）机构链型（含有3个四杆闭环）非线性的潜力相对较低，即机械利益最小。

图2 4个三副杆和4个二副杆链型

2 紧凑性

紧凑性是指系统的静态性能较好并且占有较小的空间。在运动链中，不考虑杆件的长短尺寸，判断杆件机构的紧凑性时，认为杆件和运动副的数目越少时其紧凑性越好；当杆件机构的杆件和运动副的数目相等时，就由杆件之间两杆隔开的最少运动副的个数来判断紧凑性的优劣。为了分析的方便，可以给每个杆以及运动副进行编号，图2（a）链型进行编号后如图5所示。

图3 1个四副杆，2个三副杆以及5个二副杆链型

图4 2个四副杆和5个二副杆链型

由上述紧凑性的定义，得到图2（a）链型的距离矩阵L：

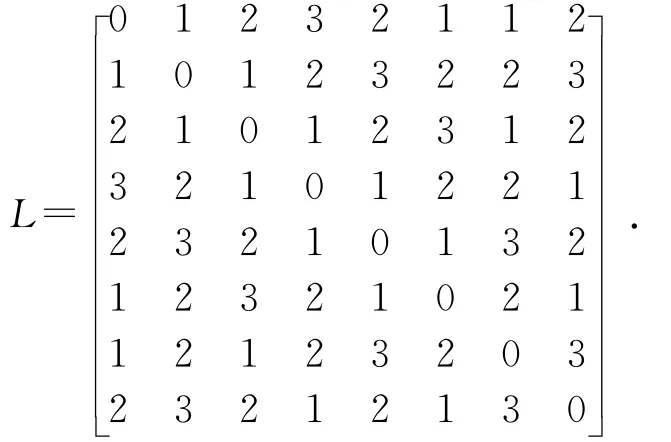
矩阵L中，元素lij是选定一杆i与任意杆j两杆之间最少运动副的个数，其中lii＝0。把矩阵L中各元素相加，得到的值越小则运动链就越紧凑。依此类推得到所有机构链型的矩阵，并将矩阵中各元素相加，得到每个链型的紧凑性值，见表1。从表1中可以看出链型图2（d）和图4（a）紧凑性较好。

图5 编号后的图2（a）

表1 八杆链型的紧凑性值

3 刚性

杆的实际刚性主要取决于杆的尺寸、弹性以及支承情况。对于图2～图4中所有的运动链，不考虑杆件的尺寸，仅将各连杆视为弹性体，定义每个杆的运动副数就等于杆的支承点数目，并且用刚度矩阵K来表示运动链的刚性，矩阵中的元素kij可按下式计算：

其中：ci，cj，cs分别为杆i，j，s的运动副数。选定杆i和任一杆j，杆i到杆j之间的路径必须是串联连接的杆，杆s为杆i与杆j之间串联的杆。如果存在多条串联路径，则选择杆件的运动副数最少的路径。由上述定义可得图2（a）机构链型的刚性矩阵为：

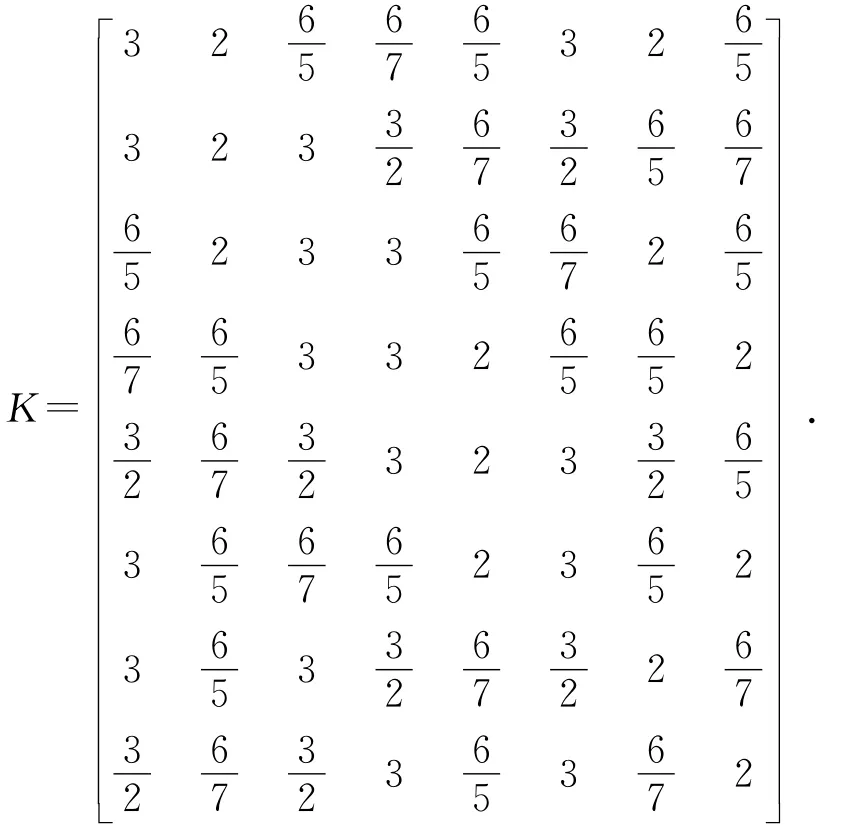
在矩阵K中，把每一行的各元素相加，得到的值即为链型中对应杆的刚度。图2（a）中杆1～8的刚度值分别为14.46，13.91，14.46，14.46，14.56，14.46，13.91，13.91，从而得到杆5的刚性比较大。把矩阵中每个元素相加得到的值表示为整个链型的刚性，其刚度值大小为114.16。同样，可以得到图2～图4中所有机构链型的刚度值，见表2，可以看出图2（d）链型刚度值较好。

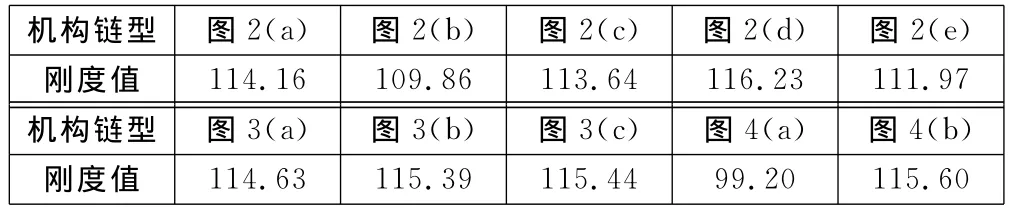
表2 八杆链型的刚度值

4 动态灵敏度

对于机构链型的动态性能，可以用动态灵敏度表示。为了反映每个机构运动链的动态灵敏度，不考虑其杆件的尺寸、大小、质量，通过机构链型中的某运动副与机架隔开的最少运动副的数目来判断其动态灵敏度的高低。再根据灵敏度的高低来判断整个机构链型的动态性能，灵敏度越低的机构链型的动态性能也就越好，反之则越差。

用矩阵D来表示整个机构链型的动态灵敏度。矩阵D中的任意元素dij是选择其中一杆作为机架并依次判断链型中的每个运动副j与机架杆i之间最少的运动副个数。图2（a）链型的灵敏度矩阵如下：

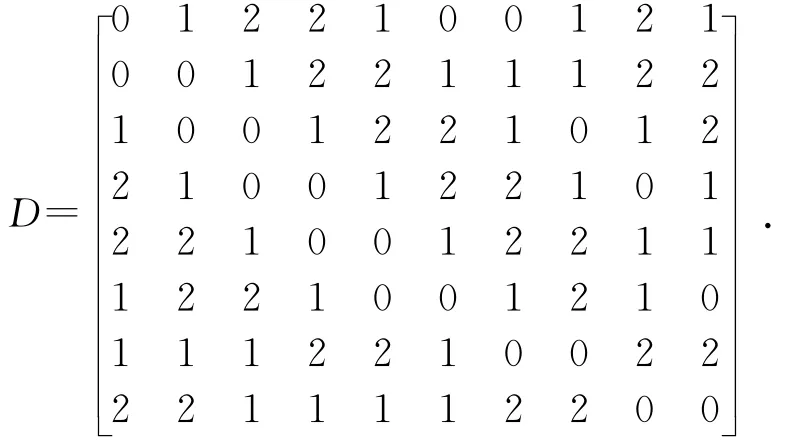
在机构链型中，杆i为机架时其动态灵敏度指数为（dimax－1）。其中，dimax为矩阵D的第i行元素中的最大值。计算得到的图2（a）链型中杆1～8依次为机架时的动态灵敏度指数为（2－1）＝1，（2－1）＝1，（2－1）＝1，（2－1）＝1，（2－1）＝1，（2－1）＝1，（2－1）＝1，（2－1）＝1，将其各值相加得到了整个机构链型的灵敏度值为8。同理，可以得到的图2～图4中所有运动机构链型的动态灵敏度指数，见表3。可知图4（b）链型的灵敏度值最低，其动态性能最好。

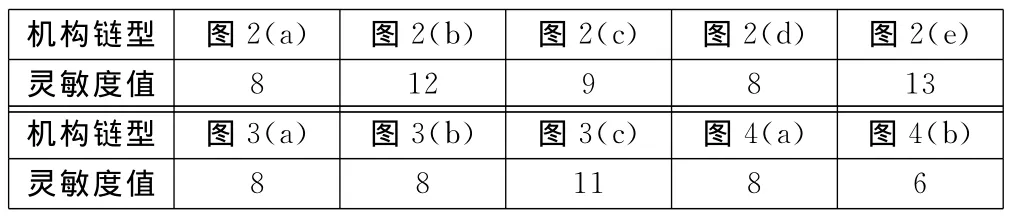
表3 八杆链型的灵敏度值

5 结语

本文对机构链型为单自由度八连杆机构的拓扑特性进行了研究、分析、计算，比较了八杆机构的10种链型结构，为设计者进行八杆机构的创新设计选择合适链型提供参考。

［1］吴舒海，陈文家.二自由度七杆机构链型和拓扑特性研究［J］.农业装备技术，2010（2）：45-48.

［2］王静平，郑阿曼，李俊萍.机构自由度为1的六杆机构链型的拓扑特性研究［J］.机械工程师，2008（8）：96-98.

［3］颜鸿森.颜氏创造性机构设计：（三）运动链数目综合［J］.机械设计，1995，12（12）：38-41.

［4］李佳，廖汉元，孔建益.平面五杆机构的机构变换及选型［J］.中国机械工程，2007，18（1）：20-22.

［5］曹惟庆.连杆机构的分析与综合［M］.北京：科学出版社，2002.

［6］李树军，杜立群.运动链和机构的拓扑特性及其性能评价［J］.东北大学学报，1997，18（6）：671-675.