基于DEA的林业建设项目绩效评价方法研究

熊跃生，王忠伟

（中南林业科技大学，湖南长沙410004）

基于DEA的林业建设项目绩效评价方法研究

熊跃生，王忠伟

（中南林业科技大学，湖南长沙410004）

对于林业建设项目的绩效评价，目前主要采用DEA方法，但是传统的CCR模型容易出现多个决策单元同时有效，造成排序困难。原因是每个决策单元都依据最大值原则选择对自己最有利的权重，计算出的效率值普遍偏高，既不合理，又难排序。在此基础上的各种改进模型对给定的信息量有一定的要求。为此提出根据统一的公共权重计算效率值，并给出信息充分、信息不充分和信息不完全充分条件下的评价模型。最后通过绩效实例，验证了该模型可以在不确定信息条件下对决策单元进行有效排序，评价结果更为合理。

林业建设项目；公共权重；DEA；绩效评价

林业是中国重要的基础产业，随着公众对生态环境的日益重视，中国不断加大对林业的财政投入，而且在政府的引导下，各种社会资本的投入也呈蓬勃之势。因此，科学建立评价模型和合理设置评价指标，对于提高林业建设项目管理水平具有重要意义。对于林业建设项目的绩效评价，目前主要采用DEA方法。Viitala and Jannincn运用DEA模型研究芬兰19个公益林的效率[1]，Kao和Yang研究了台湾的13个林区的投入产出效率[2]，赖作卿等分析了广东林业投入产出效率[3]，李春华等对中国31个省份的林业投入产出效率进行比较分析[4]，李微等对2008-2010年中国各地区林业产业效率进行了研究[5]。但是从研究结果可以看出，采用DEA方法中的基本模型（如CCR模型）进行绩效评价时，经常出现多个决策单元同时有效，使评价结果的区分度变差，进而无法排序的问题[6-10]。

区分度差究其原因主要是基本模型在对评价指标分配权重时，都采用自评权重原则选择对自己最有利的权重，而不考虑各指标间重要程度的不同，这样一来计算出的效率值就会普遍偏高。如果单纯变动决策单元数和投入产出指标数，自评权重也会随之变动，每个决策单元的效率值任然保持高水平，无法有效排序。另外，自评权重的存在，让每个决策单元都是在不同标准下计算效率值，既不公平，也不合理。因此应该根据统一的公共权重计算效率值。现有的研究一般采用两种改进方法，第一种是根据主观偏好评定公共权重[11-15]，第二种是根据客观数据引入其它模型计算公共权重[16-21]，这两种方法都存在一定的局限性。在信息充分的条件下，根据主观偏好评定公共权重比较准确，但是，在信息不充分的条件下，很可能判断失误甚至无法判断。由于有些模型对信息量的依赖比较少，在信息不充分的条件下，利用这些模型计算公共权重比较合理。总之，现有的两类改进方法分别只适合信息充分和信息不充分两种条件。有理由认为，现实情况很复杂，可能还有信息不完全充分的情况。比如投入指标信息是充分的，而产出指标信息是不充分的，甚至投入指标里面部分信息是充分的，部分信息是不充分的。针对以上方法的局限性，本文考虑将现有的两种改进方法结合起来，分别考虑信息充分、信息不充分和不完全充分条件下的公共权重计算方法，并对绩效进行评价和排序。

1 CCR模型简介

设有n个决策单元DMUk(k=1，2，…，n)，每个决策单元都有m种投入和s种产出指标。分别用＞0，＞ 0，k=l，…，n表示第j个决策单元DMUj的投入、产出向量。投入权重向量v=(v1，v2，…，vm)T和产出权重向量u= (u1，u2，…，us)T，则待评价单元的效率可以表示为

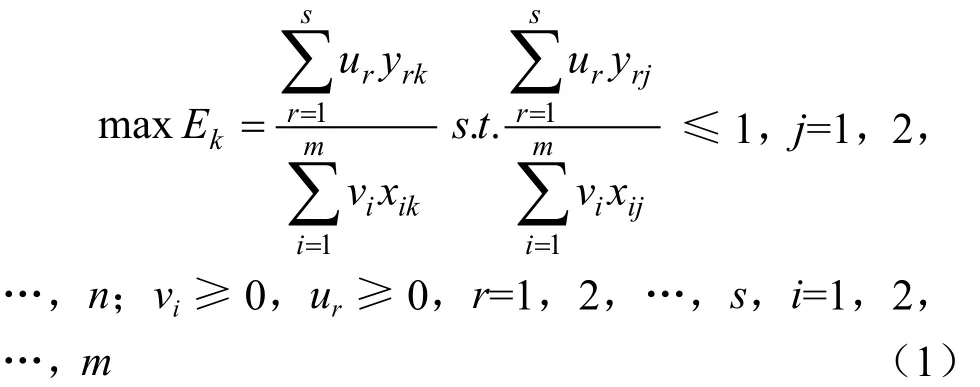
式（1）就是DEA中最基本的CCR模型，由于分式不利于求解，经过转换，可以用线性规划形式表示如下：

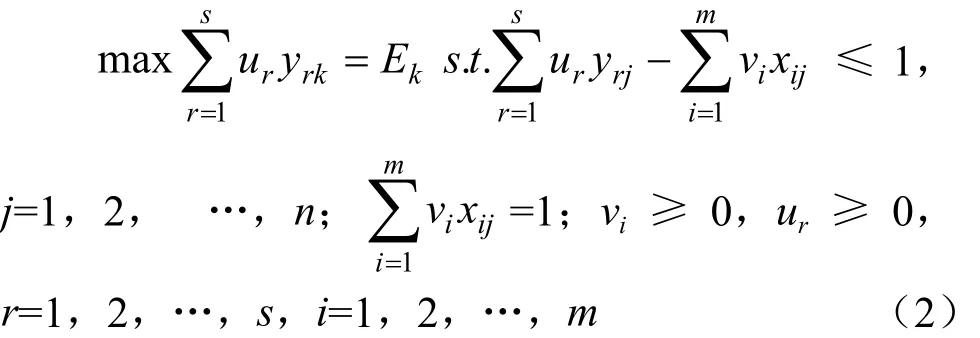
评价时一般用式（2）或式（2）的对偶模型，当最优值＜1时，则认为DMUk是非DEA有效的，当最优值=1，则认为DMUk是弱DEA有效的，当最优值1，且u*＞0，v*＞0时，则认为DMUk是DEA有效的。CCR默认采用自评权重，每个决策单元都选择对自己最有利的权重，很难满足u*＞0，v*＞0，这就会产生大量的弱有效的决策单元，使区分度变差，甚至无法排序。只有确定公共权重才能解决这一问题。根据前面的分析，在不确定信息条件下，分为三种情况讨论。

2 改进后的DEA模型

2.1 信息充分条件下的评价模型

在信息充分条件下，可以采用层次分析法（Analytic Hierarchy Process，简称AHP）确定公共权重，基本原理是将复杂的系统要素层次化，并形成阶梯层次的结构模型。通过逐层比较，建立成对比较矩阵，再对各指标赋权重，并检验结果的合理性。通过计算各层各指标的组合权重，最终确定各指标的相对权重。具体计算步骤如下：

（1）建立层次结构模型。将有关影响因素按不同属性由上而下分解成若干层次，最上层通常只有1个因素，为目标层，最下层通常为方案层，最上层与最下层之间可以有一个或多个层次，通常为指标层。

（2）构造成对比较矩阵。设某层有n个因素，用aji表示第i个因素相对于第j个因素的比较结果，令

则称为成对比较矩阵。

比较时取1～9尺度，其含义见表1。

表1 1～9尺度含义Table 1Yardstick’s meanings

（3）层次单排序及一致性检验。层次单排序即确定下层各因素对上层某因素影响程度的过程，也就是对于每一个成对比较矩阵计算最大特征根及对应特征向量，利用一致性指标、随机一致性指标和一致性比率做一致性检验。若检验通过，归一化后的特征向量即为权向量：若不通过，需重新构造成对比较矩阵。

表2 随机一致性指标 RI 的数值Table 2Values of random consistency indexes

（4）计算层次总排序并做一致性检验。层次总排序即计算最下层对目标的组合权向量，设下层B1，B2，…，Bn对上层因素Aj（j=1，2，…，m）的随机一致性指为RIj，层次单排序一致性指标为CIj，则层次总排序的一致性比率为：

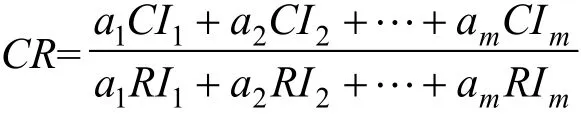
当CR＜0.1时，代表检验通过，否则需要重新构造成对比较矩阵。用vAHP表示投入指标公共权重，uAHP表示产出指标公共权重，则在信息充分条件下，可用式（3）对绩效进行评价和排序。

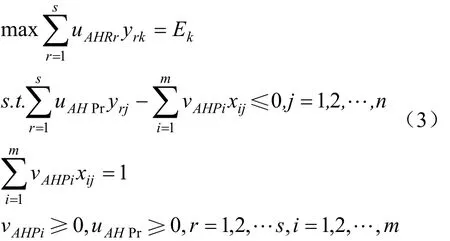
2.2 信息不充分条件下确定公共权重

在信息不充分条件下，无法根据经验对各指标重要性作出判断，这时可以采用灰色关联度（Grey Relational Analysis，简称GRA）确定权重。在一组待评的DMU中加入一个最小投入最大产出的最优DMUmax，这个最优DMUmax无疑相对于其它DMU来说是DEA有效的，以最优DMUmax的效率最大为目的确定出来的权重应该说是比较合理的，其他DMU均采用最优DMUmax的权重作为公共权重，这样就形成了统一的评价标准。

实际决策单元的投入指标、产出指标分别记为

则最优DMUmax的投入指标、产出指标分别记为且必须满足

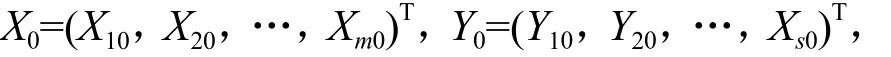
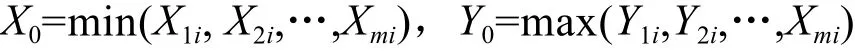
（1）投入指标公共权重

X0与Xi的关联度

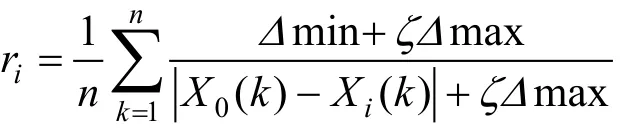
ri经归一化处理后，可得到投入指标公共权重

（2）产出指标公共权重Y0与Yi的关联度

ri经归一化处理后，可得到产出指标公共权重

则在信息不充分条件下，可用式（4）对绩效进行评价和排序。

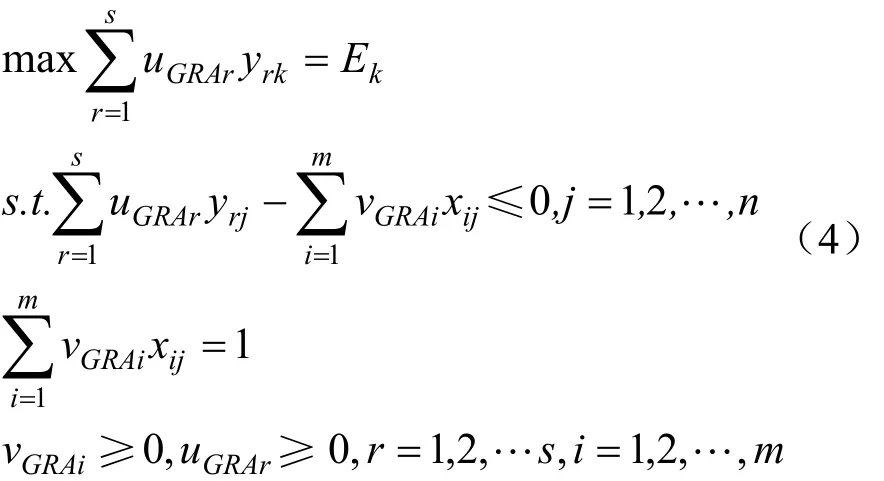
2.3 信息不完全充分条件下确定公共权重

假设1：投入指标信息是充分的，而产出指标信息是不充分的

投入指标公共权重v通过AHP法确定，产出指标公共权重u通过引入最优DMUmax的GRA法确定。则在这种条件下，可用式（5）对绩效进行评价和排序。

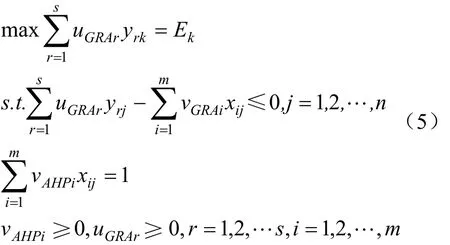
假设2：投入指标信息是不充分的，而产出指标信息是充分的

投入指标公共权重v通过引入最优DMUmax的GRA法确定，产出指标公共权重u通过AHP法确定。则在这种条件下，可用式（6）对绩效进行评价和排序。

假设3：投入指标信息是充分的，而产出指标信息部分是充分，部分是不充分的

投入指标公共权重v可以通过AHP法确定，产出指标公共权重u可以分成两部分，信息充分部分通过AHP法确定，信息不充分部分通过引入最优DMUmax的GRA法确定。则在这种条件下，可用式（7）对绩效进行评价和排序。

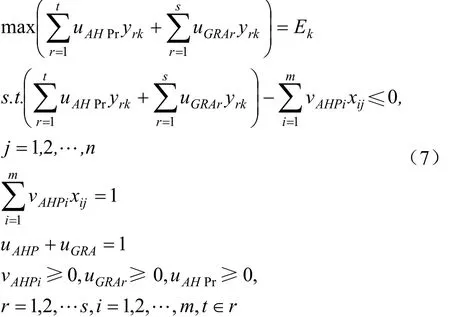
假设4：投入指标信息部分是充分，部分是不充分的，而产出指标信息是充分的

投入指标公共权重v可以分成两部分，信息充分部分通过AHP法确定，信息不充分部分通过引入最优DMUmax的GRA法确定，产出指标公共权重u通过AHP法确定。则在这种条件下，可用式（8）对绩效进行评价和排序。

假设5：投入产出指标信息都有部分是充分，部分是不充分的

投入产出指标公共权重v和u均分成两部分，信息充分部分通过AHP法确定，信息不充分部分通过引入最优DMUmax的GRA法确定。则在这种条件下，可用式（9）对绩效进行评价和排序。

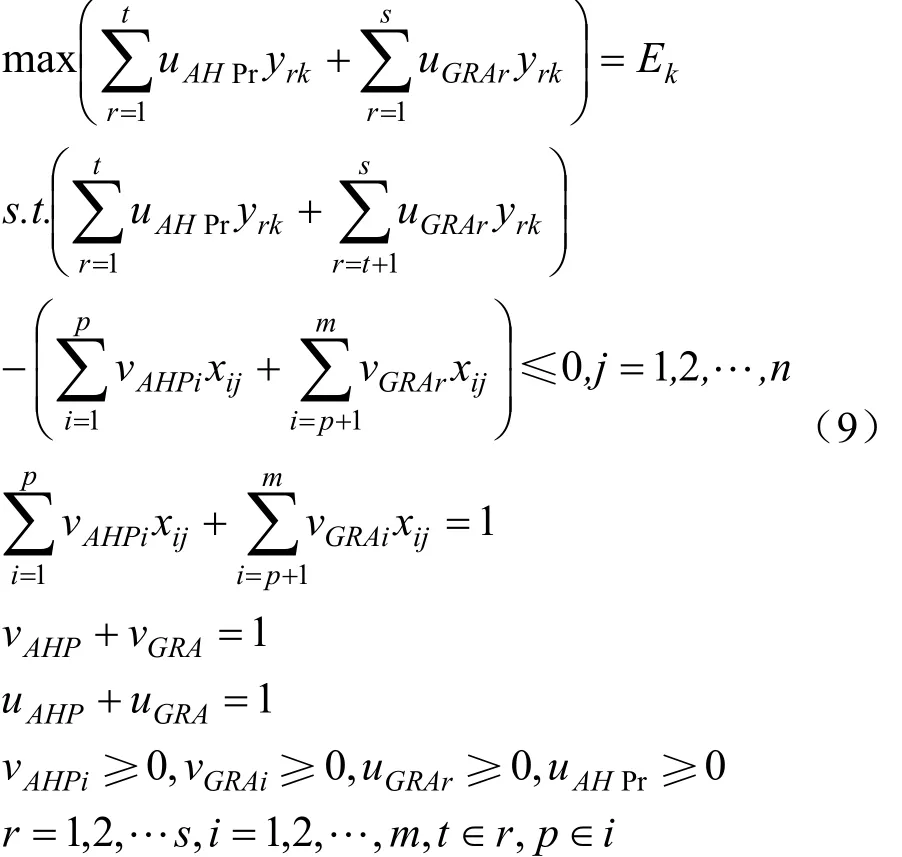
3 林业建设项目绩效评价实例

3.1 评价指标的选取

绩效是指资源配置状态，最高绩效意味着资源配置效率最大化，即用最小的投入得到最大的产出。对于林业建设项目来说，其本质是生产要素的投入，根据西方经济学理论，生产要素中最重要的就是土地、资本、劳动力和技术4种要素，因此可以将林业用地面积作为土地投入要素，固定资产投资完成额作为资本投入要素，按行业分林业从业人员年末人数作为劳动力投入要素，劳动投入率和资本投入率作为技术投入要素。不过，林业用地面积、劳动投入率和资本投入率数据不完整，最后只选取固定资产投资完成额（X1）和按行业分林业从业人员年末人数（X2）作为投入指标。

同时，林业建设项目会产生一定的经济效益、生态效益和社会效益。由于经济效益的直接表现产值最大化，因此可以用林业产业总产值来表示。社会效益体现很多方面，但比较好度量体现在改善林农生活水平方面，因此可以用林农人均收入来表示。由于生态效益的数据不易获取，最后只将林业产业总产值（Y1）和林农人均收入（Y2）作为产出指标。

3.2 绩效评价

选取中国31个省份作为决策单元，数据来源于2012年《中国统计年鉴》、2011年《中国林业统计年鉴》。假设投入指标信息是不充分的，而产出指标信息是充分的，则可用式（6）对林业建设项目绩效进行评价和排序。将原始数据标准化后得到表3数据。

投入指标公共权重v通过引入最优DMUmax的GRA法确定得到v1=0.5515，v2=0.4485，产出指标公共权重u通过AHP法确定得到v1=0.4506，v2=0.5494。计算结果见表4。

表3 中国31个省份标准化后的数据Table 3Data of China’s 31 provinces (autonomous regions) after being standardized

表4 式6和CCR模型计算结果比较Table 4Comparison of results calculated by equation 6 and CCR model

通过比较可以看出，用CCR模型进行绩效评价，区分度变差，出现8个决策单元同时有效，比例达到25.8%，造成排序困难。而采用本方法进行绩效评价，区分度良好，可以准确对所有决策单元进行排序。其中上海、江苏、浙江等地项目建设较好，效率达到或接近1，而西藏、山西、宁夏等地项目建设较差。从总体上来讲，东部和南部沿海地区要优于中部地区，西部和北部地区效率最低，与中国的经济分布区域大体相同。但像北京这样发达地区却没能进入前十，说明林业建设项目绩效并非单纯受区域经济的影响。通过进一步分析发现，北京等发达地区属规模效率递减，应该是资源利用效率不佳，而西藏、宁夏等地区属规模效率递增，应该是资源投入不足。所以像北京等发达地区应该减少资源投入，提升利用效率，青海、宁夏等欠发达地区应该增加资源投入，这样才能提高这两类地区的绩效。

4 结论

我国对林业建设项目绩效评价问题的研究比国外晚，目前相关的研究成果少，已有的成果大部分只用DEA一种方法来研究，但容易出现多个决策单元全部有效而无法排序的问题。已有的改进模型只能在信息充分和信息不充分条件下应用，在信息不完全充分条件下无法应用。本文提出改进模型，不仅可以在信息充分和信息不充分条件下应用，而且还可以在信息不完全充分条件下应用，并在林业建设项目绩效评价中实际应用。结果表明，由于确定了公共权重，评价过程更加公平，评价结果的区分度大幅提高，可以对决策单元进行有效排序。

但是，林业建设项目绩效评价的研究还处于起步阶段，这些方法和理论有待进一步深化、完善和补充。第一，本文在如何判断指标信息是否充分时只是笼统的指出根据评价者自身经验判断，实际上，可能会带来一定的盲目，在选择AHP或GRA计算公共权重时，就不可避免的带有主观评判的色彩和偏好。如何准确界定信息是否充分有待于之后继续深入探讨。第二，应进一步探讨扩展数据包络分析模型的应用范围，如分析某个林业计划的绩效，分析林业计划内各个地区、单位的林业建设绩效。从分析结果找出绩效低的原因和改进计划执行的措施。也可以用来评价林业的技术进步，地区的技术进步等。第三，由于林业用地面积、劳动投入率和资本投入率数据不完整，只选取了固定资产投资完成额和按行业分林业从业人员年末人数两个投入指标。同样，在产出指标的选取上，也只是选取了林业产业总产值和林农人均收入作为经济效益和社会效益的产出指标，没有反映出生态效益，显然，这必定对林业投入产出效率的计算带来一定偏差。因此如何解决这些不足之处将是以后研究的重点。

[1]Viitala EJ, H Janninen. Measuring the efficiency of public forestry organizations[J].Forest Science,1998, 44: 298-307.

[2]Kao C, YC Yang. Measuring the eff i ciency of forest management[J].Forest Science,1991,37(5): 1239-1252.

[3]赖作卿,张忠海.基于DEA方法的广东林业投入产出效率分析[J].林业经济问题,2008,(4):323-326.

[4]李春华,李 宁,骆华莹,等.基于DEA方法的中国林业生产效率分析及优化路径[J].中国农学通报,2011,(1)9:55-59.

[5]李 微,万志芳,郑丽娟.中国林业产业发展水平实证研究[J].商业研究,2012,(6):204-209.

[6]Golany B,Roll Y.An application procedure for DEA[J].Omega,1989,17(3):237-250.

[7]盛昭翰,朱 乔,吴广谋. DEA理论方法与应用[M].北京:科学出版社,1996:155- 312

[8]田淑英,许文立.基于DEA模型的中国林业投入产出效率评价[J].资源科学,2012,(10):1944-1950.

[9]张俊容,郭耀煌.评价指标与DEA有效的关系[J].系统工程理论方法应用,2004,(6):520-523.

[10]马生昀,王冬梅,马占新,等.多元回归在DEA方法指标降维中的应用[J].内蒙古农业大学学报:自然科学版,2012,(1):231-235.

[11]PL Brockett,A Charnes,WWCooper, et al. Data transformations in DEA cone ratio envelopment approaches for monitoring bank performances[J]. European Journal of Operational Research,1997, 98(2):250-268.

[12]Srinivas Talluri K,Paul Yoon. A cone-ratio DEA approach for AMT justification[J]. International Journal of Production Economics,2000,66(2):119-129.

[13]Zhang Songtao, Pang Haifeng, Wei Zhuangpin. Research on Partner Selection in Virtual Enterprise Based on AHP and DEA[J]. Journal of Convergence Information Technology, 2013,8(6): 1-8.

[14]李小伟,朴银玥,尹少华,等.基于层次分析法的湖南肉类企业绩效评价研究[J].中南林业科技大学学报,2011,31(4):200-204.

[15]杨晶淇,吴立潮,李春华,等.长株潭城市群土地集约利用相对效率评价的数据包络分析[J].中南林业科技大学学报,2012, 32(6):37-42.

[16]刘英平,林志贵,沈祖诒.有效区分决策单元的数据包络分析方法[J].系统工程理论与实践,2006,(3):112-116.

[17 史成东,陈菊红,张雅琪. 物流公司绩效的DEA交叉评价[J].系统工程,2010,(1):47-52.

[18]许祥鹏. 基于改进的DEA模型在效率评价中的应用[J].财会研究,2011,(6):60-62.

[19]Su-Mei Lin. Associating DEA with grey relational analysis for performance assessment of management competencies in logistic industry[J]. Journal of Statistics and Management Systems,2010,135

[20]孙 凯,鞠晓峰.基于改进DEA模型的工业企业技术创新能力评价[J].系统管理学报,2008,17(2):134-145.

[21]田淑英,许文立.基于DEA模型的中国林业投入产出效率评价[J].资源科学,2012,(10):1944-1950.

Research on forestry construction project performance evaluation based on DEA

XIONG Yue-sheng, WANG Zhong-wei
(Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

At present the DEA method is mainly employed in performance evaluation of forestry construction project. But the traditional CCR model is easy to cause multiple decision-making units being effective at the same time, thus the decision-making units can not be sorted. The reason is that each decision-making unit chooses the weight that most favourable to itself according to the maximum principle, the calculated eff i ciency values are generally on the high side, which is unreasonable and hard to sort. The improved models on this basis have some requests for the given amount of information. Therefore, the eff i ciency values should be calculated according to the unif i ed public weight, and the evaluation models are given under the conditions of suff i cient information, inadequate information and incomplete full information. Finally the model is verif i ed through performance examples that it can effectively sort the decision-making units under the condition of uncertain information and the evaluation result is more reasonable.

forestry construction project; public weight; DEA; performance evaluation

S7-9

A

1673-923X(2014)05-0118-07

2014-03-10

国家社会科学基金“农产品物流仓单质押盈利模式与风险防范研究”（11BG057）

熊跃生（1968-），男，湖南桃江人，博士研究生，研究方向：森林工程； E-mail：13786312333@163.com

王忠伟（1965-） ，男，湖南邵阳人，教授，博士生导师，研究方向：工程项目管理； E-mail：wangpmp@163.com

[本文编校：吴毅]