海河流域水质评价与预测

李亚楠，孙宝盛，张 燕

（天津大学 环境科学与工程学院，天津300072）

海河流域水质评价与预测

李亚楠，孙宝盛，张 燕

（天津大学 环境科学与工程学院，天津300072）

以海河流域为例，选择灰色关联分析法对其水质进行了评价。由于传统的灰色关联分析存在一定缺陷，故选择两种改进的灰色关联分析法进行水质评价，并比较了这两种方法的优缺点。采用对应分析法，将采样点与变量有机地结合起来进行了分析。最后使用灰色预测模型对海河流域水质情况进行了预测。结果表明：（1）将基于改进AHP法权重的灰色关联分析法与对应分析法联用可以全面认识流域水质状况，给出科学合理的评价结果；（2）海河流域污染来源主要为农业面源污染与生活污水污染。

水质评价与预测；灰色关联分析；对应分析；灰色预测模型

在近几十年里，随着经济和社会的发展，河流的纳污负荷愈来愈大。可以说河流污染已经成为当今最严重的水质问题之一。因此研究河流水质评价和预测的方法具有十分重要的意义［1］。水质评价工作开始于20世纪60年代，经过30多年的研究，水质评价的方法已是多种多样［2］。由于水质综合评价自身存在的特殊性，各水质评价方法在实际应用中各具优缺点。在水质评价中，有限的时空监测数据所提供的信息是不完全的，污染物与环境之间也存在着复杂多变的联系［3］，河流环境系统充满了灰色性。故灰色关联评价法可能具有更好的适用性。但是传统的灰色关联评价法客观性及分辨率较低，难以反映出河流水污染状态。为了克服传统灰色关联评价法的这一缺点，在以下内容中将以海河水质评价为例，采用两种改进的灰色关联评价法对海河水质进行评价分析，总结出其各自的适用性和优缺点。现有水质模型的研究大多是将水质的定性定量、空间分布及预测分开进行研究，例如水质评价模型虽然可以较好地对水质进行定性定量分析，但难以反映水质的空间分布情况。而在对水质进行定性定量及空间分布情况研究的基础上，对水质进行预测，可以了解当地水域环境质量演变趋势，进而及时发现水质恶化的原因并采取相应的治理措施。因此，本研究在对海河进行水质评价的基础上联合应用对应分析法研究海河流域样本点和变量（评价指标）之间的内在空间分布规律，最后应用灰色模型对海河水质进行预测以期对海河水质进行全面的分析，为海河流域的水质保护提供理论依据。

1 评价方法及过程

1.1 评价方法

灰色关联分析法是一种处理小样本和信息不足问题的工具［4］。它具有对数据要求较低且计算量小，便于广泛应用的优点［5］。但是传统的灰色关联分析法的计算结果分辨率低，仅能得出水质类别，难以反映出河流水污染状态［6］。

层次分析法具有简便、灵活及实用的优点［7－8］。以AHP权重代替等权，可以很好地解决传统灰色关联分析法存在的问题，同时本研究采用的改进的AHP法通过三标度比较矩阵和间接判断矩阵可以克服传统AHP法存在的主观性太强的问题，使权重确定过程趋于客观、准确。

模糊数学是一种用于研究界限不分明的问题的数学工具［9］，它是最成功的灰箱模型之一［10］。模糊灰色关联分析可以将二者的优点结合在一起，有效地避免了灰色关联分析结果分辨率低及模糊数学易造成数据丢失的缺点。

1.2 评价过程

1.2.1 基于改进AHP法权重的灰色关联分析

（1）构造A—B判断矩阵B＊ij。根据各断面所在区域的水功能区、保护类别等因素建立三标度比较矩阵。令

则三标度比较矩阵A 为（aij）m×m。

构造间接矩阵Bij，并转换为拟优一致矩阵B＊ij，计算B＊ij的最大特征根λmax及相应的最大特征向量。并进行归一化处理得到原则层B中元素i对目标层A 的相对重要性权重W（Ci），i＝1，2，…，n。

（2）构造Bi—C判断矩阵。构造单因子评价矩阵D，对D中各行元素进行两两比较，得到Bi—C判断矩阵，求最大特征值和相应的特征向量，并由矩阵的随机一致性比例CR进行一致性检验.最终求得指标层C中第k个元素对原则层B中第i个元素的相对重要性权重W（Cik），i＝1，2，…，n；k＝1，2，…，m。

（3）层次总排序及一致性检验。相对重要性权重Wk＝W（Ci）WiCik，k＝1，2，…，m。

层次总排序的一致性检验，Ic，IR应采用均值：

式中：k——阶数。

（4）确定比较数列和参考数列。以各断面各水质评价因子的监测值作为参考数列，以地表水质量分级标准值为比较数列。xj（k）表示j级水质标准中第k项评价因子的标准值；yi（k）表示第i个断面中第k项评价因子的监测值。

（5）计算差值数列，两级最大差和两极最小差。

（6）计算关联度与关联系数。

本文取ρ＝0.5。

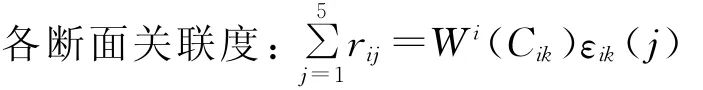
1.2.2 模糊灰色关联分析

（1）确定比较数列和参考数列。设有n种待评价因子，则对原始监测数据：

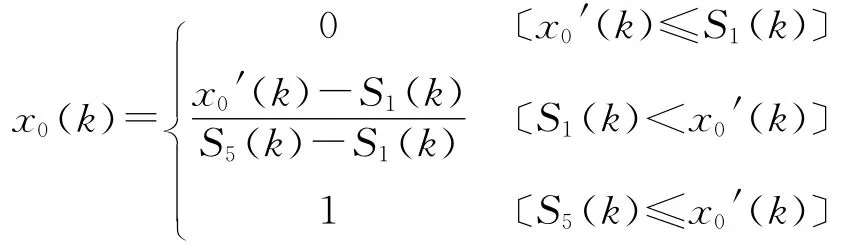
式中：k＝1，2，…，n，表示第k种污染物；

｛S0（k）｝＝｛S1（k），S2（k），…，S5（k）｝为对应的第k种污染物的水质分级标准；

｛x0′（k）｝＝｛x0′（1），x0′（2），…，x0′（n）｝表示 第k种污染物的原始监测数据序列；

｛x0（k）｝＝｛x0（1），x0（2），…，x0（n）｝为第k种污染物初值化后的监测数据数列，设为参考序列。

上述的公式适合数值愈大、污染愈重的评价因子，对于如溶解氧（DO）等数值愈大、污染程度愈轻的指标其基本表达式不变，只需改变条件中符号的方向。令：

则：｛xi（k）｝＝｛xi（1），xi（2），…，xi（n）｝为第k种污染物标准化后的水质分级标准，设为比较序列。

（2）计算关联度及关联系数。关联度与关联系数的计算方法与AHP灰色关联分析中的计算方法相似。其中评价因子的权重采用污染贡献率法来确定。

（3）加权平均计算水质等级。水质等级的确定方法与AHP灰色关联分析中的方法相同。

2 应用案例

2.1 数据来源

海河流域地跨北京、天津、河北、河南、山东、山西、内蒙古及辽宁8省（自治区、直辖市），流域总面积3.18×105km2。选取《全国主要流域重点断面水质自动监测周报》中属于海河水系的5个断面为研究对象，分别为河北省张家口市八号桥、北京市密云古北口潮河、天津市果河桥黎河、北京市门头沟沿河城永定河、天津三岔口海河，这5个断面总体反映了京津地区的水质状况。采用2004—2012年监测周报中的数据，每个监测断面选取溶解氧（DO）、高锰酸钾指数（CODMn）和氨氮（NH＋4—N）3个监测指标作为研究对象进行年平均计算处理后得132个数据进行水质评价。

2.2 评价结果与分析

2.2.1 基于改进AHP法权重的灰色关联分析 各断面所属功能区详见表1。层次结构图如图1所示，层次总排序结果详见表2，该方法的水质评价结果如图2所示。

图1 海河流域水质评价层次结构

表1 各监测断面所属功能区

表2 灰色关联分析各层次总排序

图2 基于改进AHP法权重的灰色关联分析结果

2.2.2 模糊灰色关联分析 计算得到比较数列为：COD的比较数列：｛0，0.1538，0.3077，0.6154，1｝；NH＋4—N的比较数列：｛0，0，1892，0.4595，0.7297，1｝；DO的比较数列：｛0，0.2727，0.4545，0.8182，1｝。

模糊灰色关联分析法的水质评价结果如图3所示。由图2—3知两种分析方法在断面B2，B3，B4的评价结果大致相同，这是因为两种方法都是根据样本的实际情况和重要程度，通过计算，得出相对合理的权重进行灰色关联分析得出评价结果。两种方法在断面B1，B5的评价结果有较大差距，这是因为以污染贡献率来确定权重时当某种污染物超标较为严重时该种污染物的作用会被夸大。对比两种方法，可以看出模糊灰色关联分析概念直观，计算方便，容易理解，但以污染贡献率来确定权重的方法不能考虑各种污染物的协同作用效果且当某种污染物超标较为严重时评价结果会受较大影响；基于改进AHP法权重的灰色关联分析法可以对不同性质的污染因子一致对待，对多断面的区域水环境评价进行综合评价，但其主观性较模糊灰色关联分析要强，且计算也更繁琐。

图3 模糊灰色关联分析结果

3 对应分析法在海河流域水质状况分析中的应用

水质评价方法并不能揭示样本点和变量（评价指标）之间的内在空间分布规律，为了解决这一问题，将采用对应分析法来研究海河流域水质状况的内在空间分布规律。

3.1 数据预处理与计算步骤

为了消除量纲差异对对应分析结果的影响以及满足对应分析的数据要求，采用污染贡献率法对数据进行预处理。对应分析的主要步骤为：（1）建立水质监测数据矩阵；（2）对矩阵作对应变换；（3）作R型因子分析；（4）作Q型因子分析；（5）得水质指标变量和样点的主因子平面点聚图。采用SPSS 20完成对应分析。

3.2 数据分析

以2012年数据为例，其变量和样品点的主因子载荷平面投影图如图4所示。

（1）从整体上看，5个样点被分成3个区。Ⅰ区主要受COD（C1）的影响：B4；Ⅱ区主要受 DO（C3）的影响：B1，B2；Ⅲ主要受NH＋4—N（C2）的影响：B3，B5。

（2）从变量对主因子轴的影响分析。各离子坐标（载荷）绝对值反映了其与不同主因子轴的相关性程度大小，在两个变量主因子轴上载荷绝对值最大的分别为COD（C1）和DO（C3），说明海河水质受有机物污染的影响比较大。

（3）将因子载荷平面投影图与实际区域联系起来，可以发现河北张家口八号桥（B1）的污染最严重，对主因子轴进行单独分析也可发现，该断面受NH＋4—N得影响也较大。其原因可能是此处为水库入口，水库上游城市化进程的加快，工业和城乡生活污水量及农田化肥农药使用量逐年增加，而污水处理水平较低，污水直接流入上游河道，致使是水资源污染严重，且从地形上看，入库出有一个较大的拐弯，水流入库后流速减缓使污染物大量沉积。天津三岔口（B5）水质较差，其原因可能是周围是农村地区，两岸大量施放的含氮肥料随雨水进入海河干流，同时未经处理的生活污水直接经沟渠排入干流使该断面氨氮含量较高。北京市密云古北口（B2）、天津果河桥（B3）、北京市门头沟沿河城（B4）断面的水质较好，原因可能是不断加强和完善的水资源保护措施发挥了重要作用，且北京市门头沟沿河城断面是官厅水库的出口处，经过水库水的充分混合稀释，水质可能会有提高。

（4）对应分析法的结果与基于改进AHP法权重的灰色关联分析的结果较为相近，故在有条件的情况下可优先选择该法进行水质评价。

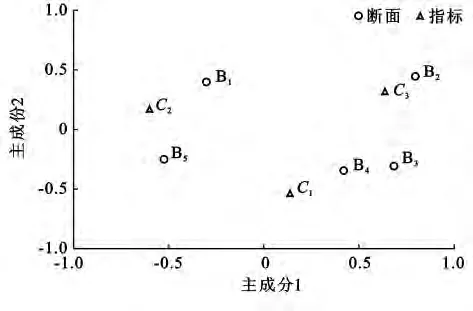
图4 对应分析因子载荷平面投影图

4 水质预测

采用GM（1，1）模型进行水质预测。灰色系统理论是中国学者邓聚龙在20世纪80年代创立的一门新兴横断学科，其实质是将一些已知的数据序列，通过一定的方法处理，使其由散乱状态转向规律化，然后利用微分方程拟合，并由外延进行预测。由于其对于信息不完整或不完全的实际情况具有良好的适用性，故其在水质预测中得到了较为广泛的运用。

4.1 分析方法

分析的步骤主要为：（1）取得累加生成数列；（2）进行光滑性检验；（3）进行指数规律检验；（4）确定数据矩阵；（5）计算参数列；（6）确定微分方程，求时间相应函数；（7）精度检验，当精度不合要求时，采用残差模型对原模型进行修正。

4.2 预测结果与分析

预测结果如图5所示。从图5可以看出，各个断面的溶解氧值都比较高处于一个较好的水平，而氨氮和高锰酸盐指数却有超标的情况发生，说明海河流域水质受这两个指标影响比较大，海河流域的主要污染物可能是生活污水和农业废水。河北省张家口市八号桥（B1）、天津市三岔口（B5）水质较差，而其它3个断面水质状况要好一些。灰色模型对于数据有异常值或波动较大情况不能准确预测，如河北省张家口市八号桥（B1）的氨氮值预测。分析结果表明，河北省张家口市八号桥的污染最严重，其原因可能是受上游污染物排放的影响。且从地形上看，入库出有一个较大的拐弯，水流入库后流速减缓使污染物大量沉积。天津市三岔口水质较差，其原因可能是受周围农业面源污染影响。

北京市密云县古北口、天津市果河桥、北京市门头沟沿河城断面的水质较好，原因可能是不断加强和完善的水资源保护措施发挥了重要作用，且北京门头沟沿河城断面是官厅水库的出口处，经过水库水的充分混合稀释，水质可能会有提高。

图5 高锰酸盐指数浓度、氨氮浓度和溶解氧浓度变化趋势

5 结论

（1）基于改进AHP法权重的灰色关联分析法与模糊灰色关联分析法都可根据样本的实际情况和重要程度，通过计算，得出相对合理的权重然后进行灰色关联分析得出评价结果。

（2）基于改进AHP法权重的灰色关联分析法可以得到各个指标对水质情况的影响程度大小，其结果与对应分析的结果较为一致，将两种方法结合在一起，可以全面认识流域水质状况，给出科学合理的评价结果。

（3）灰色预测模型对于数据有异常值或波动较大情况不能准确预测。

（4）研究结果表明，海河流域污染来源主要为农业面源污染与生活污水污染。

［1］ Zhang Ruibin，Qian Xin，Li Huiming.Selection of optimal river water quality improvement programs using QUAL2K：A case study of Taihu Lake Basin，China［J］.Science of the Total Environment，2012，431（1）：278－285.

［2］ 王肖肖，张妙仙，徐兵兵.模糊标识指数与对应分析法在水质评价中的联合应用［J］.环境科学学报，2012，32（5）：1227－1235.

［3］ 张静，孙省利.海水环境质量模糊—灰色关联评价及应用［J］.广东海洋大学学报，2011，31（6）：68－72.

［4］ lp W C，Hu B Q，Wong H.Applications of grey relational method to river environment quality evaluation in China［J］.Journal of Hydrology，2009，379（3／4）：284－290.

［5］ 王敬敏，郭继伟，连向军.两种改进的灰色关联分析法的比较研究［J］.华北电力大学学报，2005，32（6）：72－76.

［6］ 梁小俊，张庆庆，许月萍，等.层次分析法—灰关联分析法在京杭运河杭州段水质综合评价中的应用［J］.武汉大学学报：工学版2011，44（3）：312－316.

［7］ Alessio L，Ashraf L.Review of the main developments in the analytic hierarchy process ［J］.Expert Systerms with Applications，2011，38（11）：14336－14345.

［8］ 李凤伟，杜修力，张明聚，等.改进的层次分析法在明挖地铁车站施工风险辨识中的应用［J］.北京工业大学学报，2012，38（2）：167－172.

［9］ Ocampo D W，FerréH N，Domingo J L.Assessing water quality in rivers with fuzzy inference systems：A case study［J］.Environment International，2006，32（6）：733－742.

［10］ Zhou Shangming，Gan J Q.Low－level interpretability and high－level interpretability：A unified view of datadriven interpretable fuzzy system modelling［J］.Fuzzy Sets and Systems，2008，159（23）：3091－3131.

Evaluation and Prediction of Water Quality in Haihe River Basin

LI Yan－nan，SUN Bao－sheng，ZHANG Yan
（School of Environmental Science and Engineering，Tianjin University，Tianjin300072，China）

This paper used gray correlation analysis method to evaluate the water quality of Haihe River basin.However，the traditional grey correlation analysis has drawbacks due to subjectivity in calculating relatedness.To overcome this defect，this paper chosen two kinds of improved gray correlation analysis methods for the water quality evaluation，and compared the advantages and disadvantages of the two methods.The combined application of improved gray correlation analysis method and correspondence analysis method can reach to scientific and reasonable evaluation conclusions.Meanwhile，this paper predicted water quality using grey prediction model.The results showed that：（1）Combination of the improved AHP weights of gray relational analysis and correspondence analysis can provide a nice way to understand basin water quality and reach to a rational evaluation result；（2）The main sources of pollution in the Haihe River basin is agricultural nonpoint source pollution and sewage pollution.

water quality evaluation and prediction；gray correlation analysis；correspondence analysis；grey prediction model

B

1000－288X（2014）02－0177－05

X824

10.13961/j.cnki.stbctb.2014.02.038

2013－05－20

2013－06－20

天津市自然科学基金重点项目“污水处理中EPS，SMP与生物多样性技术研究”（07JCZDJC02100）

李亚楠（1989—），女（汉族），河北省邢台市人，硕士研究生，研究方向为环境评价。E－mail：Leexiao＿xiang＠126.com。

孙宝盛（1957—），男（汉族），天津市人，副教授，主要从事环境影响评价、水处理等方面的研究。E－mail：baosheng＿sun＠sina.com。