基于粒子群优化神经网络算法的深基坑变形预测方法

刘 贺，张弘强，刘 斌

1.吉林大学交通学院，长春 130022

2.吉林农业工程职业技术学院，吉林 四平 136001

3.辽宁城建设计院有限公司，辽宁 抚顺 113008

0 引言

随着地下空间的不断开发，深基坑工程呈现出规模不断扩大、深度不断加深的发展趋势，因此，确保基坑施工安全成为深基坑工程的首要任务。深基坑工程的变形不仅涉及土的力学特性，还受到土与结构相互作用、地下水位和环境温度等因素的影响，开挖过程其变形具有明显的时间和空间效应。所以，深基坑安全施工是一个动态、复杂的系统工程。深基坑变形预测是确保深基坑施工安全的一项重要措施，在施工方案调整和施工风险规避等方面具有重要的实用价值［1］。

针对深基坑变形预测方法，国内外专家学者展开了相应的研究，将数值模拟方法应用到基坑变形预测中［2－4］。该方法的基本思想是建立基坑有限元分析模型，在有限元分析模型中输入计算参数，对基坑的变形进行计算。由于深基坑工程是一个动态非线性过程，加上内部和外部参数的不确定性，导致有限元模型的输入参数难以准确计算。

由于数值模拟方法难以对基坑变形进行准确预测，系统分析方法在基坑变形预测中得以广泛应用。常用的基坑变形预测系统分析方法主要包括时间序列分析［5］、灰色系统理论［6］、模拟退火算法［7］、遗传算法［8－9］以及人工神经网络理论［10－11］等。 其中人工神经网络理论具有较强的自适应和自学习能力，对于高度复杂的非线性问题具有良好的模拟能力，能较好地模拟基坑变形的发展规律。针对复杂多因素影响系统，人工神经网络能够克服其他系统分析方法的不足，建立准确的预测模型，实现基坑变形预测。但神经网络算法存在对初始权值和阀值较为敏感、容易陷入局部极小值和收敛速度慢等缺点。利用粒子群优化算法对其进行优化，能够改善神经网络性能，提高深基坑变形预测的准确性［12］。

粒子群优化算法（particle swarm optimization，PSO）是由J.Kennedy和R.C.Eberhart［13］根据鸟群觅食过程中的迁徙和聚集现象提出的一种基于群体智能原理的非线性优化算法。它采用种群的全局搜索策略和简单位移－速度模式在解空间搜索最优解；通过粒子的不断更新，完成解空间的动态全面搜索［14］；采用粒子群优化算法改进神经网络，通过粒子迭代求出全局优化初始权值和阈值，应用于神经网络，可以提高神经网络的性能［15］。

笔者采用粒子群算法对神经网络模型中的阀值和初始权值进行优化，建立了基坑变形预测模型，提出了深基坑变形预测方法。将前期实测变形数据作为神经网络的输入参数，对神经网络进行训练，训练的神经网络能够对基坑后续变形进行准确预测。

1 基坑变形预测方法的基本理论及原理

1.1 神经网络模型的设计

三层BP网络能够模拟复杂非线性的输入输出关系［16］。笔者采用三层BP神经网络作为基坑变形预测模型进行基坑变形预测。采用的BP神经网络结构由输入层、隐含层和输出层组成。

1.1.1 输入层设计

基坑的变形受开挖形式、开挖深度、地下水位以及土压力等众多因素的影响。随着基坑的开挖，变形是一个连续动态过程，具有极强的时间效应。把影响因素直接作为神经网络输入变量，难以对基坑变形进行准确预测。综合考虑各因素对变形的影响，把前期实测变形值作为神经网络模型输入变量，预测基坑后续变形值。

1.1.2 隐含层设计

确定隐含层的节点个数是隐含层设计的主要任务。隐含层节点个数过多，会降低神经网络算法的泛化能力，增加样本训练时间；节点个数过少，则会降低神经网络算法获取训练样本有效信息的能力。笔者采用公式（1）对隐含层节点数进行估算，确定隐含层由10个节点组成，即

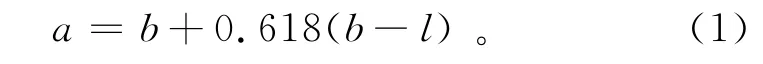
式中：a为隐含层节点数；b为输入层节点数；l为输出层节点数。

1.1.3 输出层设计

Pureline函数是一个线性函数，函数形式如图1所示。笔者采用Pureline函数作为输出层的传递函数，能够使输出层对输出值具有较好的敏感性。

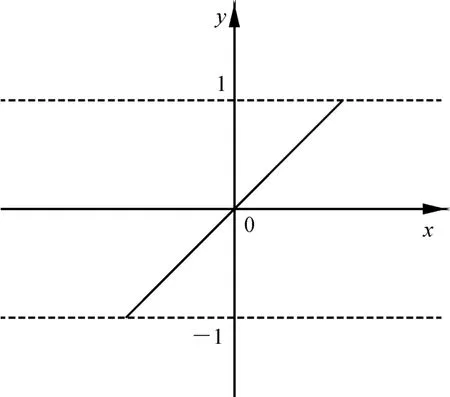
图1 Pureline函数曲线Fig.1 Pureline function curve

1.2 粒子群优化算法

粒子群优化算法［14］的基本思想为M个无质量、无体积的粒子构成一个粒子群，在D维搜索空间内以一定速度飞行，寻找全局最优解，飞行位置和速度分别由位置向量和速度向量确定。粒子在每一时刻跟踪2个极值运动，一个是粒子群的全局最优位置，另一个是粒子自身最优位置。

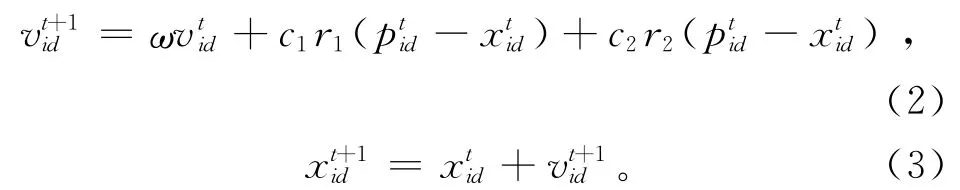
粒子群优化算法通过迭代搜寻每个粒子的当前最优解，采用适应度函数评价解的优劣程度，比较粒子的适应度函数值，确定全局最优解。

1.3 粒子群优化神经网络算法

粒子群优化神经网络算法中，粒子的个体极值点和全局最优极值点以及神经网络模型中权值和阈值的优化终止条件都是基于粒子的适应度来确定的。粒子的适应度函数为

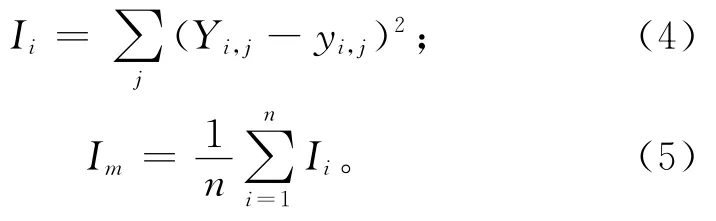
式中：Yi，j为第i个样本的第j个理想输出值；yi，j为第i个样本的第j个实际输出值；n为样本数；m＝1，2，…，M，M为粒子种群规模，即粒子数。

将粒子群优化算法的误差要求作为神经网络算法阈值和权值的优化终止条件，误差采用下式进行计算：

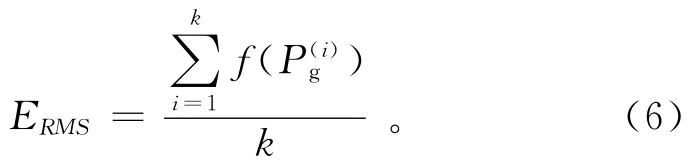
粒子群优化神经网络算法的流程如下：

1）确定神经网络结构。

2）初始化神经网络权值和阈值。

3）建立粒子群与权值和阈值的关系，对粒子群进行初始化。

4）将基坑前期实测变形值作为输入值，进行神经网络训练，通过式（4）、（5）计算适应度，对适应度进行比较和评价，按式（2）、（3）更新每个粒子的位置和速度。

5）通过式（6）计算粒子群优化算法的误差。如果误差满足要求，则终止优化，输出权值和阈值优化结果；若误差不满足要求，则继续优化，重复步骤4），直到误差满足要求。

6）在神经网络模型中，采用优化后的权值和阈值进行样本训练，形成基坑变形预测模型。

7）根据已有的实测数据，利用神经网络模型预测测点即将发生的变形。

2 实际工程应用

2.1 工程概况

选取长春市火车站综合交通换乘中心北广场为实体工程。基坑东西方向长550m，南北方向宽150 m；深度为7.45～14.00m，采用明挖施工形式。由于基坑东侧较浅，采用两级放坡开挖，网喷混凝土护面对土质边坡进行防护。其余3面开挖深度较深，采用1级放坡开挖，坡率为1∶1。同时采用钻孔灌注桩和网喷混凝土护面进行防护，围护桩径1.0m，中心间距1.2m。勘察结果表明，拟建场地地层沉积具有一定的规律性，场地地层主要由三部分组成：地表一般分布有道路结构层和人工堆积杂填土层，厚度为1.00～4.20m；中间部分为第四系冲击黏性土和冲洪积砂土，由粉质黏土、黏土和粗砂组成，其中粉质黏土的厚度为5.1～21.8m，黏土厚度为5.20～10.80m，粗砂厚度为0.70～4.00m；最下层为白垩纪泥岩。

对整个基坑开挖过程中的基坑变形进行了监测，在基坑周围共布设34个水平位移测点和32个地面沉降测点，测点布置如图2所示（其中H表示水平位移测点，V表示地面沉降测点）。由于在基坑监测过程中实际的测点数较多，为了验证本文方法的有效性，只对8号水平位移测点H8和9号地面沉降测点V9的数据进行预测。这两个位移监测点位于基坑长度的中点，即深度最深的位置。

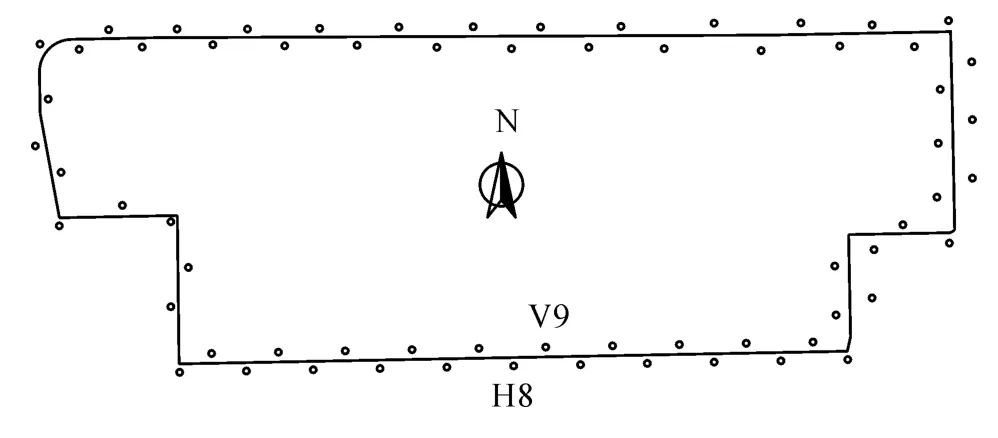
图2 测点布置示意图Fig.2 Layout of deformation measuring point

2.2 基坑变形预测模型参数选取

利用前15次的监测数据来构造训练样本。指定测点的某次监测数据为输出，测点之前的6次监测数据为输入，则该测点的6次输入数据和1次输出数据构成了1组训练样本。利用前15次的监测数据共构建了10组训练样本。

BP神经网络模型具有6个输入变量和1个输出变量，隐含层具有10个节点。根据连接权值和阈值的个数，确定粒子群的规模为20。

2.3 预测结果

利用粒子群优化神经网络预测方法对8号水平位移测点和9号地面沉降点的变形数据进行了预测，并利用均方根误差（RMSE）和平均百分比误差（MAPE）对预测结果进行评价：

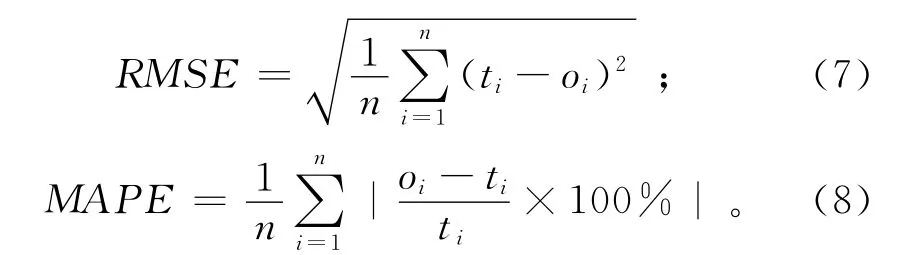
式中：ti为第i个实测值；oi为第i个预测值；n为数据数。

8号测点的水平位移预测结果如图3所示，9号地面沉降点的预测结果如图4所示。

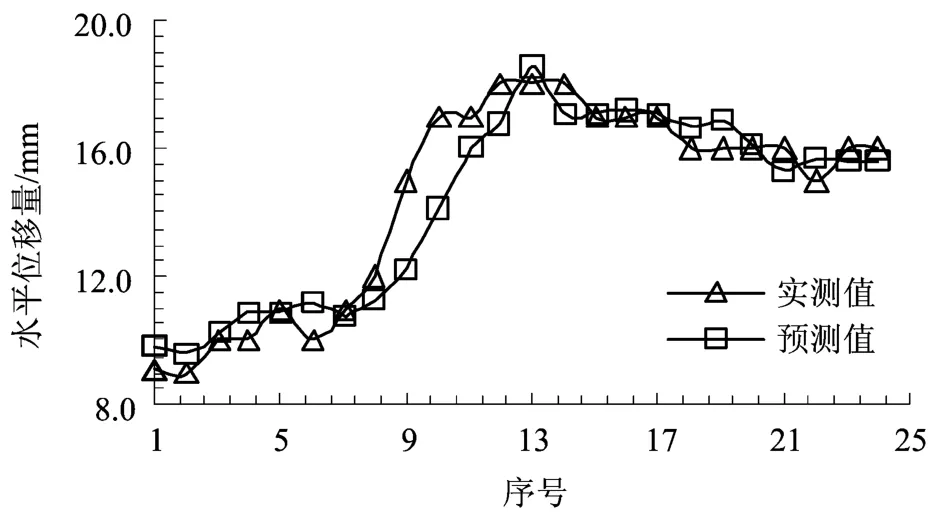
图3 8号水平位移测点的预测结果Fig.3 Prediction result of No.8horizontal displacement measuring point

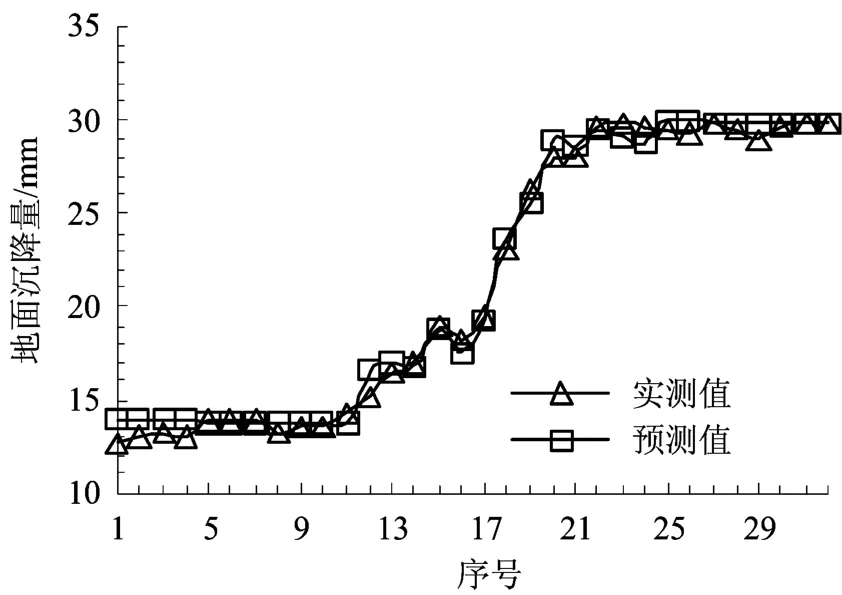
图4 9号地面沉降点的预测结果Fig.4 Prediction result of No.9land subsidence point

由预测结果可知：1）8号水平位移测点预测结果的RMSE＝3.78%，MAPE＝5.48%；9号地面沉降点预测结果的RMSE＝5.62%，MAPE＝3.23%。一般来说，在基坑监测过程中，变形监测的误差小于8%即可，本文预测误差均小于该误差限值，这说明本文提出的方法可以较为准确地预测出深基坑开挖过程中的变形。2）8号水平位移测点和9号地面沉降点的变化趋势不一致，这是由于2个测点的观测时间不同导致的，根据施工进度，9号地面沉降点的布置及观测时间要比8号水平位移测点早3个月左右。

3 结论与建议

1）针对神经网络算法在变形预测中存在的问题，采用粒子群优化算法对神经网络模型参数进行优化，从而形成了基于粒子群优化神经网络算法的深基坑变形预测方法。该方法仅利用前期的实测变形数据来预测同一测点的后续变形值。实际应用表明，变形预测误差均小于6%，满足基坑变形监测的要求，说明本方法在深基坑开挖的变形预测中可得到有效应用。

2）基坑变形是评价基坑开挖过程中安全性的一个重要参数，本方法可以预测出一个较为准确的理论参考值，在基坑监测中可以把变形实测值与该理论参考值进行比较来评价基坑的安全性。本研究为同类工程的变形监测和预测提供了一种不同的思路。

在部分监测数据失真或误差过大的情况下，该方法如何给出一个准确的预测值，还需要进行进一步的研究，以便提高该方法的实用性。

（References）：

［1］王宁，黄铭.开挖作用下的深基坑变形神经网络监测模型［J］.上海交通大学学报，2009，43（6）：990－994.Wang Ning，Huang Ming.Deformation Monitoring Artificial Neural Network Model of Deep Foundation Pit Considering the Excavation Effect［J］.Journal of Shanghai Jiaotong University，2009，43（6）：990－994.

［2］陈兴贤，骆祖江，安晓宇，等.深基坑降水三维变参数非稳定渗流与地面沉降耦合模型［J］.吉林大学学报：地球科学版，2013，43（5）：1572－1578.Chen Xingxian，Luo Zujiang，An Xiaoyu，et al.Coupling Model of Groundwater Three Dimensional Variable－Parametric Non－Steady Seepage and Land－Subsidence［J］.Journal of Jilin University：Earth Science Edition，2013，43（5）：1572－1578.

［3］刘志凯，郑毅，左广州.基坑开挖与土钉支护的数值模拟［J］.吉林大学学报：地球科学版，2004，34（增刊1）：103－106.Liu Zhikai，Zheng Yi，Zuo Guangzhou.Numerical Simulation of the Foundation Digging and the Soil Nail Protection［J］.Journal of Jilin University：Earth Science Edition，2004，34（Sup.1）：103－106.

［4］曹国金，姜弘道.信息化施工技术在地下工程中的应用［J］.岩土力学，2002，23（6）：795－799.Cao Guojin， Jiang Hongdao.Application of Information Technology in Underground Engineering［J］.Rock and Soil Mechanics，2002，23（6）：795－799.

［5］袁金荣，赵福勇.基坑变形预测的时间序列分析［J］.土木工程学报，2001，34（6）：55－59.Yuan Jinrong，Zhao Fuyong.Time Series Analysis of Foundation Pit Deformation Prediction［J］.China Civil Engineering Journal，2001，34（6）：55－59.

［6］陈晓斌，张家生，安关峰.GM（1，1）与 GM（2，1）模型在基坑工程预测中的应用［J］.岩土工程学报，2006，28（增刊）：1401－1405.Chen Xiaobin， Zhang Jiasheng， An Guanfeng.Application of GM（1，1）Model and GM（2，1）Model in Prediction of Foundation Pit［J］.Chinese Journal of Geotechnical Engineering，2006，28（Sup.）：1401－1405.

［7］张发明，庞正江，陈祖爆，等.糯扎渡电站溢洪道边坡稳定分析及系统锚固方法［J］.岩土力学，2005，（增刊1）：255－259.Zhang Faming，Pang Zhengjiang，Chen Zubao，et al.Slope Stability Analysis of Nuozhadu Power Station Spillway and System Anchoring Method［J］.Rock and Soil Mechanics，2005，（Sup.1）：255－259.

［8］周海清，陈正汉.面向对象的深度搜索遗传算法及其工程应用：I：算法与程序［J］.岩石力学与工程学报，2005，24（11）：1996－2002.Zhou Haiqing，Chen Zhenghan.Object－Oriented Depth Search Genetic Algorithm and Its Engineering Application：I：Algorithm and Program［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（11）：1996－2002.

［9］周海清，陈正汉.面向对象的深度搜索遗传算法及其工程应用：II：算法与程序［J］.岩石力学与工程学报，2005，24（12）：2194－2206.Zhou Haiqing，Chen Zhenghan.Object－Oriented Depth Search Genetic Algorithm and Its Engineering Application：II：Algorithm and Program［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（12）：2194－2206.

［10］Mayoraz F，Vulliet L.Neural Networks for Slope Movement Prediction［J］.The International Journal of Geotechnics，2002（2）：153－174.

［11］贺志勇，郑伟.基于BP神经网络的深基坑变形预测［J］.华南理工大学学报：自然科学版，2008，36（10）：92－96.He Zhiyong，Zheng Wei.Deformation Prediction of Deep Foundation Pit Based on BP Neural Network［J］.Journal of South China University of Technology：Natural Science Edition，2008，36（10）：92－96.

［12］周蕾.粒子群算法的改进及其在人工神经网络中的应用［D］.西安：西安电子科技大学，2010.Zhou Lei.Improved Particle Swarm Optimization Algorithm and the Application of Artificial Neural Network［D］.Xi’an：Xi’an University of Electronic Science and Technology，2010.

［13］Kennedy J，Eberhart R C.Particle Swarm Optimization［J］.Proceedings of the IEEE International Joint Conference on Neural Networks，1995，4：1942－1948.

［14］纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京：科学出版社，2009.Ji Zhen，Liao Huilian，Wu Qinghua.Particle Swarm Optimization and Application［M］.Beijing：Science Press，2009.

［15］韩月娇.粒子群算法的改进及其在BP神经网络中的应用［D］.南昌：南昌航空大学，2012.Han Yuejiao.Improvement on Particle Swarm Algorithm and Its Application in BP Neural Network［D］.Nanchang：Nanchang Aeronautical University，2012.

［16］Mehrjoo M，Khaji N，Moharrami H，et al.Damage Detection of Truss Bridge Joints Using Artificial Neural Networks［J］.Expert Systems with Applications，2008，35：1122－1131.