基于虚拟线圈假设的涡流制动器制动力矩计算

胡东海，何 仁

(江苏大学汽车与交通工程学院，江苏镇江212013)

涡流制动器［1］在交通运输行业上应用十分广泛，商用汽车和高速列车上都装备有不同形式的涡流制动器.同时，涡流制动器还应用在国民经济的其他领域，它主要与系列电动机配套.广泛应用于冶金、建筑、化工、食品、机床、电梯、轮船等行业.高速列车上使用的涡流制动器有直线型涡流制动器与旋转型涡流制动器.直线型涡流制动器［2］安装在转向架上而旋转型涡流制动器安装在列车车轮两侧［3］.在卡车和客车上应用的主要是旋转型涡流制动器，又称之为“电涡流缓速器”.该涡流制动器主要安装在传动轴上或变速器后端，是对摩擦制动系统的补充，防止在下坡行驶摩擦制动器过热而失效［4］.制动力矩作为涡流制动器的重要设计指标，对涡流制动器的新产品设计和改型优化有重要的意义.笔者针对现有的涡流制动器制动力矩计算方法存在的问题，提出基于虚拟线圈假设的涡流制动器制动力矩计算方法并利用某型电涡流缓速器验证该计算方法的正确性.

1 国内外研究现状及问题的提出

国外对于涡流制动器制动力矩的计算方法研究一脉相承，偏向于求解麦克斯韦方程组进行制动力矩的计算.C.Stoica等［5］根据麦克斯韦方程组利用有限元方法分析了旋转型涡流制动器的磁感应强度与涡电流的大小和分布情况;K.K.Tan等［6］根据麦克斯韦方程组对直线涡流制动器的磁场、涡流的大小与分布进行了分析，推导了制动力矩的计算公式;S.Anwar［7］采用最小二乘法拟合试验曲线，在假设温度一定的条件下拟合制动力矩与激励电流和转速的关系，通过参数识别，建立制动力矩与转速的数学模型作为电涡流缓速器控制器的控制模型.

国内使用涡流制动器制动力矩的计算方法根据对涡流作用区域的简化方法分为2种:①将转子盘制动区域简化方式分为一根根铁棒，即铁棒式;②将转子盘上的制动区域划分为一个个圆形，即圆盘式.何仁等［8］提出了铁棒假设的计算方法，该方法假设转子盘是由无数根长度为转子盘半径且过圆心的铁棒组成，转子盘转动时，铁棒切割磁感应线而产生涡流，根据法拉利电磁感应定律带电导体在磁场运动，产生了作用于铁棒上的制动力;何仁［4］提出了基于圆盘假设的电涡流缓速器制动力矩的计算方法，该方法假设在旋转转子盘上与磁极相对的位置存在有限个半径与铁芯半径相等，厚度为透入深度的圆盘，当励磁线圈通电后，旋转的圆盘中的磁通量呈余弦变化，根据法拉利电磁感应定律在圆盘中产生感应电流阻碍圆盘的运动，即产生制动力矩;郭其一等［9］将该方法引入直线型涡流制动器制动力矩计算中;杨效军等［10］将该方法运用在转筒式和自励式缓速器上取得了很好的效果.

以上2种对于涡流制动器制动力矩的简化计算模型相比于国外的计算模型具有推导清晰、计算简便等优点，更加适合于工程计算，但是这些涡流制动器制动力矩的计算公式中引入经验参数，因为涡流制动器在高速区域存在去磁现象.文献［4］中在进行磁路计算时利用涡流折算系数Ke来等效涡流去磁效应的影响，取Ke=2.文中没有给出Ke的具体计算方法以及Ke的影响因素，这就影响了对于涡流制动器制动力矩的精确计算与优化设计.

笔者在圆盘假设的基础上，提出一种新的涡流制动器制动力矩的计算方法，将圆盘涡流作用区域的涡流假设为并螺线管线圈，推导涡流制动器的气隙磁感应强度、制动功率和制动力的计算公式.

2 基于虚拟线圈假设的制动力矩推导

以旋转型涡流制动器为例，介绍基于虚拟线圈假设的制动力矩计算方法.在推导涡流制动器制动力矩过程中所做的假设:①线圈绕组产生的磁通量分布在铁芯直径内，忽略漏磁现象;②转子盘简化为一定厚度的环形金属圆环;③ 转子盘的电阻率、相对磁导率为常数，其值不随温度变化;④ 不考虑磁路的磁饱和以及磁滞损耗的影响，且忽略磁极之间的相互影响［4］.

2.1 圆盘假设

在涡流制动器中，转子盘在励磁线圈的磁场中旋转会感应出涡电流，由于肌肤效应涡电流主要分布在转子盘靠近磁极两侧的表层中，且随透入深度变大按指数规律衰减，透入深度随涡电流频率的提高而减小.计算中透入深度［11］为

式中:δ为等效透入深度，m;ρ为运动导体的电阻率，Ω·m;μ0为真空磁导率，H·m-1;μ1为转子盘的相对磁导率;ω为磁场变化角速度，rad·s-1.

圆盘假设示意图如图1所示.根据圆盘式涡流制动器的计算理论［4］，在旋转转子盘上与磁极相对的位置，存在个数为k、直径为D、厚度为δ的圆盘.

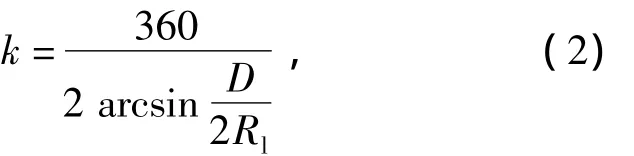
式中Rl为转子盘中心半径，m.

当转子盘与磁极有相对运动时，通过圆盘的磁通量发生变化，从而产生感应电动势和感应电流.

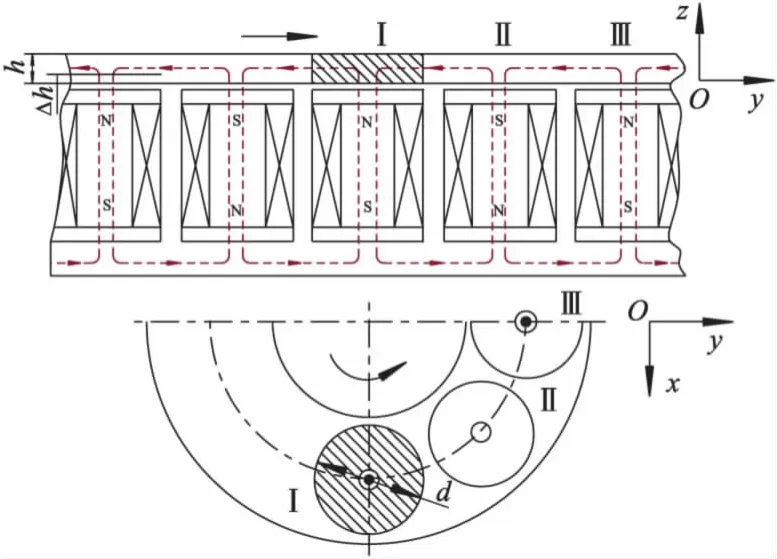
图1 圆盘假设示意图

2.2 涡流密度计算

当转子盘以一定转速旋转时，每个圆环所包围的圆形区域的磁通量是不断变化的，变化过程为Φ→0→-Φ→0→Φ，可以把这个变化规律看成是按余弦变化，磁通量变化表示为

式中:B为气隙磁感应强度，T;S为圆环面积，m2.

式中:Np为励磁线圈磁极对数;n为转子盘转速，r·min-1.

为了计算涡流制动器的计算功率，把圆盘看成由无数个半径大小不同的，宽度为dr且厚度为涡流肌肤深度的闭合圆环组成的，由此可知在由闭合圆环内磁通量变化而产生的感应电动势为

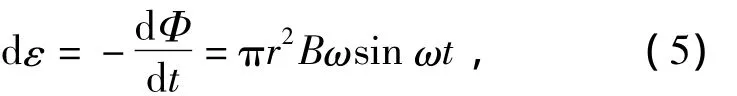
该闭合圆环的等效电阻为

则该闭合圆环上的涡电流有效值为

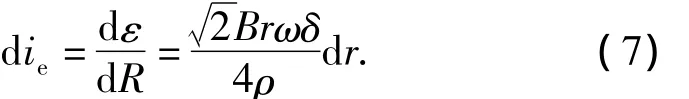
2.3 磁路分析

涡流制动器的磁路示意图如图2所示.图2a为磁路的基本结构，忽略漏磁的影响可以将图2a简化为图2b的简化磁路图形式.

由图2b可以得到整个磁路回路所通过的总磁阻为

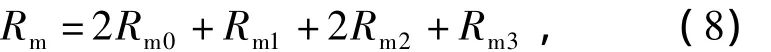
式中:Rm0为气隙的磁阻，H-1;Rm1为圆环的磁阻，H-1;Rm2为1个定子磁轭的磁阻，H-1;Rm3为1个定子磁芯的磁阻，H-1.

因为圆环、定子磁轭和定子磁芯都是用软磁材料制成，它们的磁阻相对于气隙磁阻来说很小，可以忽略不计，所以整个磁路回路的总磁阻近似为

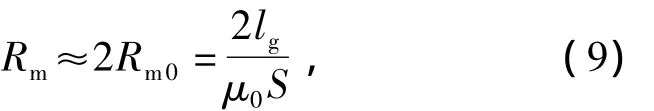
式中lg为气隙长度，m.

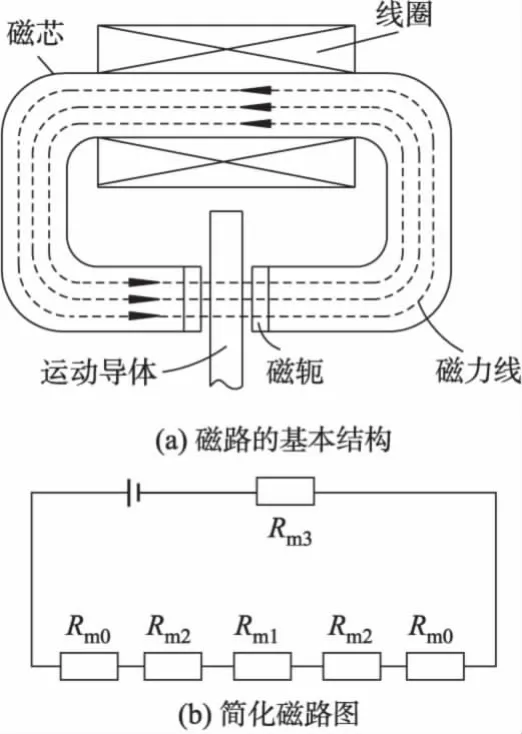
图2 磁路示意图

2.4 气隙磁场感应强度计算

计算涡流制动器的制动力矩时，主要考虑气隙磁场的磁感应强度.涡流制动器工作时，圆环内会产生涡旋状电流，这些涡流产生磁场与励磁线圈产生的磁场始终相反，对励磁线圈产生的磁场有不同程度的削弱作用，这就是通常所说的去磁效应.由式(7)可以看出圆环中的涡流有效值的大小与转子盘转速成正比.当转子盘转速较低时，产生的涡流不大，去磁效应对电磁线圈产生的磁场的影响也不大.但是当转子盘转速不断升高时，转子盘中的涡流强度越来越大，去磁效应对励磁线圈产生的磁场的影响也随之增强.

气隙磁场的磁场感应强度B有励磁线圈和涡流共同激励而成，其中由励磁线圈产生的磁感应强度为B1、圆环内涡流产生的磁感应强度为B2.气隙磁场的磁场感应强度为

励磁线圈产生的磁动势F1由线圈匝数和通入线圈的励磁电流确定:

式中:N为电磁线圈的线圈匝数，匝;I为通入励磁线圈的励磁电流，A.

得出励磁线圈在气隙中产生的磁感应强度为

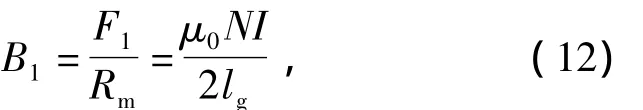
根据毕奥-萨法尔定律，励磁线圈在定子铁芯中产生的磁场为

由于气隙的影响励磁线圈在铁芯中产生的磁场由B'1衰减为B1，其比值为

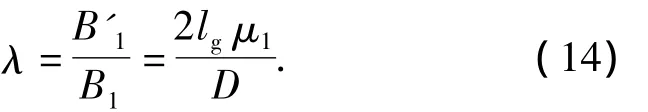
为了在计算过程中避免出现经验系数，根据上文对于励磁线圈产生磁场的分析比较，提出涡流作用区域的涡流圆环等效成绕有线圈的铁芯，假设虚拟线圈中通过的电流为die，匝数为1，铁芯直径为D.根据毕奥-萨法尔定律得到该虚拟线圈在虚拟铁芯中产生的磁感应强度为

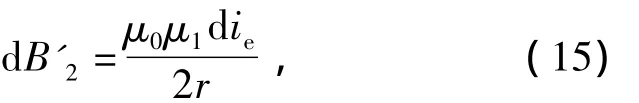
可得虚拟线圈产生的气隙磁感应强度为

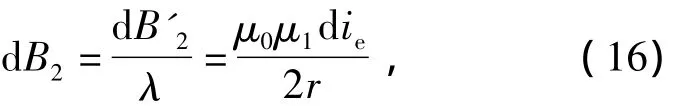
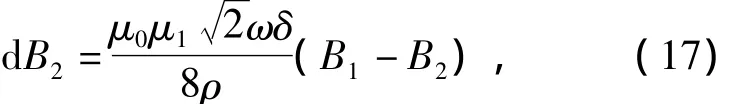
其中该微分方程的初值条件为r(0)=0，B2(0)=0，化简可得虚拟线圈产生的气隙磁感应强度为

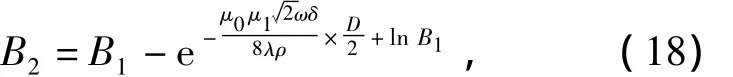
根据式(7)，(10)，(16)得出计算虚拟线圈产生的气隙磁感应强度的微分方程为

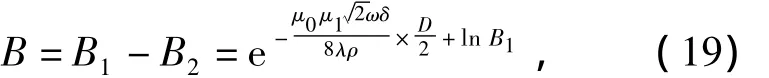
整个气隙磁感应强度的推导过程中没有对铁芯的形状和运动导体(这里的转子盘)的运动方式做任何限制，所以该推导过程同样适合直线型涡流制动器、转筒式涡流制动器以及其他形式的涡流制动器.

2.5 制动力矩的计算

由式(5)和(6)可以求出该闭合圆环上所产生的瞬时涡流热功率为

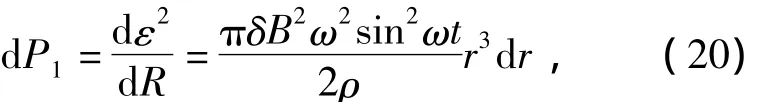
综合式(10)-(18)计算得到转子盘内的磁感应强度为

积分可得转子盘上每个圆盘上所产生的瞬时涡流热功率为

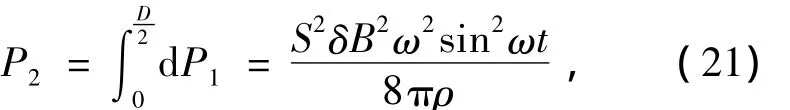
每个圆盘上所产生的有效功率为

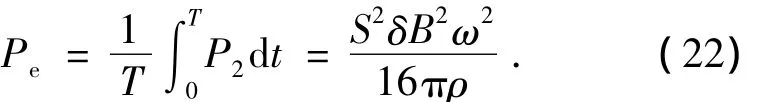
涡流制动器的能量转化也遵循能量守恒定律的.转子盘中涡电流所产生的热能总量与转子盘的动能变化量是相等的，即涡电流产生的热功率等于涡流制动器的制动功率.由此可知涡流制动器的总制动功率为

根据P=Tωn，ωn为转子盘角速度，rad·s-1.由式(19)，(23)得到涡流制动器的制动力矩为

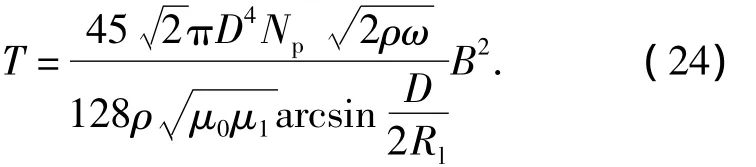
3 计算实例与分析

以江苏大学江苏省汽车工程重点实验室与江苏永亚汽车零部件制造有限公司合作开发的电涡流缓速器为例，进行计算分析与试验验证.分析的电涡流缓速器的基本结构参数如下:转子盘的中心半径Rl=210 mm;磁芯直径D=87 mm;气隙lg=3 mm;8个电磁线圈，构成4组励磁，每个线圈匝数N=340匝;电压U=24 V;线圈励磁最大电流I=125 A.缓速器制动力矩的理论计算与试验曲线比较如图3所示.

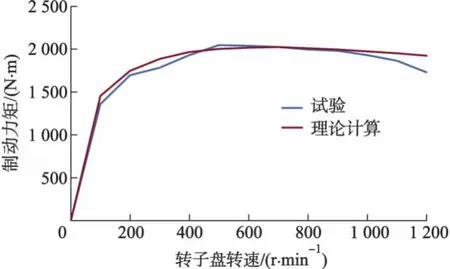
图3 理论计算与试验曲线

从图3可以看出:当转子盘转速小于500 r·min-1时，制动力矩随转子盘转速的增大而增大;当转子盘转速达到500 r·min-1时，制动力矩达到峰值，当转速超过500 r·min-1时，由于涡流去磁效应的影响，制动力矩随转子盘转速的增加而减小.只有在转速超过1 200 r·min-1时，理论制动力矩与试验值才开始出现较大误差，说明基于虚拟线圈假设的制动力矩计算方法克服了经验参数的限制，能够很好地模拟涡流制动器的制动力矩随转子盘转速的变化情况.

4 结论

提出了将闭合圆环虚拟线圈化的方法，推导了气隙磁感应强度、制动功率和制动力的计算公式，该计算公式能够清楚表达涡流制动器制动功率与各个参数之间的关系;采用理论推导的计算公式对电涡流缓速器的制动力矩进行计算分析，能够很好地模拟涡流制动器的制动力矩随转子盘转速的变化规律;该涡流制动器制动力矩的计算公式中不含有经验系数，可以用来作为涡流制动器的优化设计.

References)

［1］Gay S E，Ehsani M.Parametric analysis of eddy-current brake performance by 3-D finite-element analysis ［J］.IEEE Transactions on Magnetics，2006，42(2):319-328.

［2］Edwards J D，Jayawant B V，Dawson W R C，et al.Permanent-magnet linear eddy-current brake with a nonmagnetic reaction plate［J］.IEE Proc Electr Power Appl，1999，146(6):627-631.

［3］应之丁.涡流制动技术在高速列车上的应用［J］.电力机车与城轨车辆，2004，27(5):19-22.Ying Zhiding.Application of eddy current brake technology on high-speed trains［J］.Electric Locomotives＆Mass Transit Vehicles，2004，27(5):19-22.(in Chinese)

［4］何 仁.汽车辅助制动装置［M］.北京:化学工业出版社，2005.

［5］Stoica C，Melcescu L，Lefter E，et al.Computation of the characteristics eddy current electromagnetic brake for a bicycle，by the finite element method 3D［C］∥12th International Conference on Optimization of Electrical and Electronic Equipment.Piscataway，USA:IEEE，2010:436-440.

［6］Tan K K，Huang S N，Teo C S，et al.Damping estimation and control of a contactless brake system using an eddy current［C］∥2010 8th IEEE International Conference on Control and Automation.Piscataway，USA:IEEE，2010:2224-2228.

［7］Anwar S.A parametric model of an eddy current electric machine for automotive braking application［J］.IEEE Transactions on Control Systems Technology，2004，12(3):422-427.

［8］何 仁，衣丰艳，何建清.电涡流缓速器制动力矩的计算方法［J］.汽车工程，2004，26(2):197-200.He Ren，Yi Fengyan，He Jianqing.A computation method for braking torque of eddy current retarder［J］.Automotive Engineering，2004，26(2):197-200.(in Chinese)

［9］郭其一，黄世哲，吴伟银，等.磁浮列车涡流制动热效应研究［J］.铁道学报，2012，34(1):29-33.Guo Qiyi，Huang Shizhe，Wu Weiyin，et al.Research on pyrometric effect on eddy current brake for meglev train［J］.Journal of the China Railway Society，2012，34(1):29-33.(in Chinese)

［10］杨效军，何 仁.自励式缓速器制动力矩控制方法［J］.江苏大学学报:自然科学版，2009，30(3):256-260.Yang Xiaojun，He Ren.Control method of braking torque for self-excited retarder［J］.Journal of Jiangsu University:Natural Science Edition，2009，30(3):256-260.(in Chinese)

［11］刘存香，何 仁，胡春花.轿车电磁制动与摩擦制动集成系统的性能试验［J］.江苏大学学报:自然科学版，2012，33(5):508-512.Liu Cunxiang，He Ren，Hu Chunhua.Performance experiment of integrated system electromagnetic and frictional brakes with car［J］.Journal of Jiangsu University:Natural Science Edition，2012，33(5):508-512.(in Chinese)