对流密码Helix的代数故障攻击

陈 浩，王 韬，刘会英，周 平，冯晓云（.军械工程学院 信息工程系，河北 石家庄050003；.南京理工大学 计算机科学与技术学院，江苏 南京0094）

0 引 言

模加运算［1］广泛地应用在流密码，轻型分组密码，哈希函数等设计中，对采用模加运算的密码算法安全性分析近年来已成为密码分析学的研究热点。Helix作为一种典型模加运算结构的流密码，采用轮函数迭代，交叉使用逐位异或，模232加和循环移位3种运算来提供复杂的非线性，增强算法安全性，对其安全性的研究对其他具有模加运算结构的密码有很大的借鉴意义。

代数故障攻击［2］由Courtois在eSmart 2010会议上首次提出，它用代数分析方法建立密码算法代数方程组，利用注入故障获取错误密文，将故障差分转化为等效方程组，然后通过求解方程组进行密钥恢复。目前代数故障攻击处于起步阶段，相关研究较少，主要有Mohamed等于2011年对流密码Trivium 提出的代数故障攻击［3］，攻击仅需2个故障和420个密钥流比特即可恢复Trivium 全部的内部状态，显著的提高了故障信息的利用率。由于该方法仅针对Trivium 算法结构，对具有模加运算结构的流密码并不适用。

本文对Helix首次提出一种代数故障攻击。针对算法中模232加运算，提出一种通用的代数故障攻击模型，并通过选择明文和故障注入，建立Helix在该模型下的代数方程组，使用CryptoMiniSAT 解析器求解方程组恢复密钥信息。实验结果表明，580次故障注入即可恢复Helix工作密钥除最高位外的248比特信息，剩余8比特密钥信息可以通过穷举得到。

1 Helix算法简介

Helix面向软件实现，支持可变的密钥长度 （最长256比特），使用长度为128 比特初始向量，以字为单位进行运算。

1.1 符号说明

为论述方便起见，基本符号见表1。

表1 基本符号及说明

1.2 Helix轮函数

Helix算法轮函数如图1所示，由图1可知轮函数交叉使用异或，模232加，循环移位运算操作。

图1 Helix轮函数结构

1.3 Helix密钥扩展

Helix使用工作密钥（K0，…，K7），初始向量（N0，…，N3），轮编号i和用户密钥U 的长度（U） （0≤（U）≤32）来进行密钥扩展。整个密钥扩展分为两步，第一步将用户密钥U 转换为工作密钥；第二步将工作密钥转换成轮子密钥。

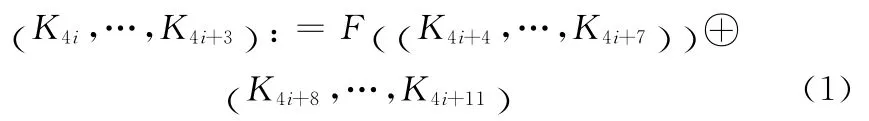
其中，i＝7，…，0。在第二步中，首先将初始向量扩展成8个字Nk：＝（k mod 4）－Nk－4（mod 232），其中K＝4，…，7，则轮子密钥由式（2）－式（4）产生

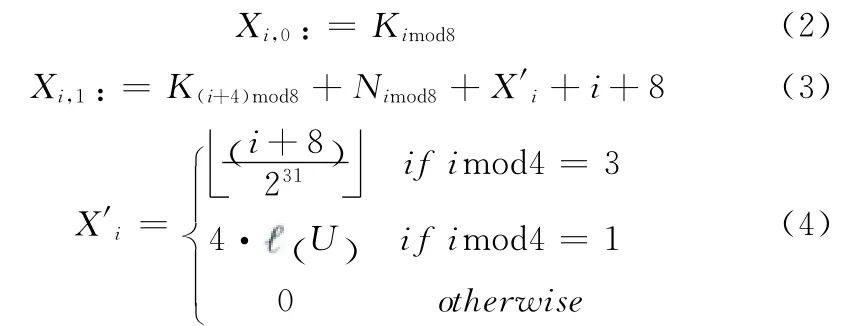
1.4 算法初始化

Helix在加密第一个明文P0前，从i＝－8开始运行8轮轮函数，运行到i＝－1时，完成初始化。初始值的设定是依照式 （5）－式 （7）来设定的

1.5 算法加密过程

2 模2n 加代数故障攻击模型

分析流密码Helix算法结构可知，Helix的安全性主要依赖模加运算，因此对Helix的代数故障攻击实质就是对模加运算的代数故障攻击。本节对模加运算提出了一种通用的代数故障攻击模型，并给出了该模型下代数方程组的构建。

2.1 代数故障攻击一般过程

如图2所示，对流密码代数故障攻击主要可分为3步：第一步，利用流密码加密算法结构建立关于内部状态或者密钥的代数方程组；第二步，向流密码加密算法引入随机故障使中间状态产生差分以获取有关内部状态或者密钥的额外信息，利用这些额外信息构建新的关于内部状态或者密钥的代数方程组；第三步，利用基于可满足性问题［4］，基于伪随机化问题［5］，基于Grbner［6］基等方法求解第一步和第二步构建的方程组，进而恢复内部状态或者初始密钥信息。本文使用CryptoMiniSAT 解析器进行密钥求解，使用方法见文献 ［7］。

图2 代数故障攻击一般过程

2.2 故障模型

本文采用随机单比特翻转故障模型，即假设攻击者具有下列能力：

（1）能够正确运行密码算法，对明文信息P 进行加密得到正确的密文C；

（2）能够向密码任意位置注入随机单比特故障使密码内部状态某个比特发生翻转 （0→1或1→0），并对明文信息P 加密得到错误密文C′；

（3）能够反复多次向密码注入故障，并且能够重启密码设备恢复初始状态。

2.3 代数方程组构建

由2.1节可知，对模加运算的代数故障攻击方程组构建可分为两步：根据模加运算特点构造代数方程组；注入随机单比特故障，利用故障信息建立额外代数方程组；为了更好的说明代数方程组的构建，首先给出模加运算的定义。

定义 设X，Y，Z∈GF （2n），X＝ （xn－1，xn－2，…，x0），Y ＝ （yn－1，yn－2，…，y0），Z＝ （zn－1，zn－2，…，z0），x0，y0，z0分别表示X，Y，Z 的最低位，则GF （2n）上的模加运算可表示为

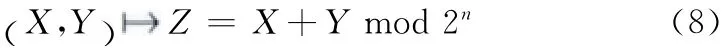
（1）利用模加运算特点构造代数方程组；

根据文献 ［8］，可以将式 （8）等价转换成GF（2）上的如式 （9）、式 （10）所示的方程组

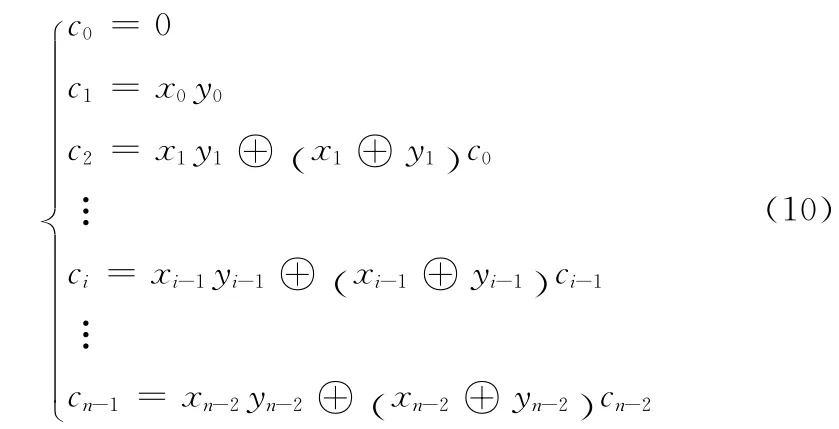
其中，ci表示进位，且有c0＝0，所以根据式 （9）、式（10）可以将GF（2n）上的模加运算转换成GF（2）上的代数方程组。

（2）利用故障信息构建代数方程组；

一般而言，由于模加运算在密码算法结构中的位置不同，向模2n加运算结构注入随机单比特故障α∈GF（2n），α＝ （εn－1，εn－2，…，ε0），存在下列两种情况：

1）已知注入的随机故障α，正确输出Z 和错误输出Z′；

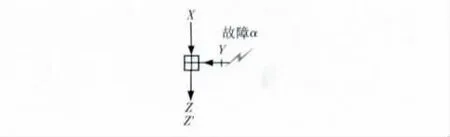
图3 第一种情况

如图3所示，故障值α和正确和错误输出Z 和Z′均已知，则根据故障信息可以得到如式 （11）所示的方成组

同式 （8），我们可以将式 （11）转化成GF（2）上的代数方程组，如式 （12）所示

2）已知注入的随机故障α，正确输出和错误输出差分ΔZ；

设ΔZ＝β，β＝ （δn－1，δn－2，…，δ0），如图4 所示，已知正确输出和错误输出的差分β则可以得到如式 （13）

图4 第二种情况

同式 （8），将式 （14）等价转化成GF（2）上的代数方程组，得到如下式 （15）－式 （17）

综合上述两种情况可以构建模加运算在GF（2）上的代数方程组，通过多次故障注入，可以构建足够多的代数方程组，对方程组进行求解可以恢复X，Y 的值。值得指出的是，由文献 ［9］知，虽然式 （11）所对应的方程组系统包含了全部X，Y 的比特信息，但由于方程中的最高位不提供任何解的信息，因此通过求解式 （11）可以恢复X，Y全部的前n－1比特信息，式 （13）所对应的方程组系统只包含了X，Y 的前n－1比特信息，因此同样只能恢复X，Y 的前n－1比特信息。

3 Helix代数故障攻击

对Helix的代数故障攻击可分为3步，第一步在Helix第i（i＞8）轮，选择不同明文Pi的值得到不同的密钥流，使用本文2.3节提出的方法构建代数方程组求解出C 值；第二步通过在指定位置注入随机故障求取D 的值，进而求出密钥Xi，1的值；第三步，根据密钥扩展算法，重复第一步第二步恢复出全部的密钥信息；下面将详细论述上面的攻击过程。

3.1 恢复C 值

步骤1 随机选择明文Pi，运行密码设备得到相应的密钥流，则有式 （18）成立

步骤2 重启密码设备，改变明文Pi使新的明文满足P′i＝PiΔ得到新的密钥流 （）′，则有式 （19）成立

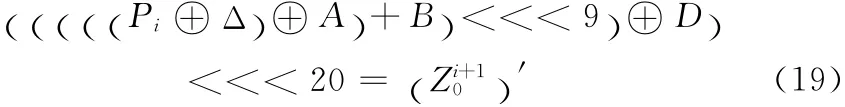
对式 （18）和式 （19）求差分可以得到式 （20）

在式 （20）中令φ＝PiA 则可将式 （20）转换为式（21）

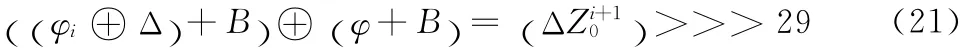
显然式 （21）与2.3节中的式 （9）对应，采用2.3节中的方法将式 （21）转换成二元域上的方程组。

步骤3 改变步骤2中的Δ值并重新执行步骤2，构建足够多的代数方程组；

步骤4 对步骤1～步骤3构建的代数方程系统进行求解，恢复φ，B，C；

3.2 恢复密钥Xi，1

步骤1 使用3.1节明文Pi，运行密码设备得到密钥流Zi＋10，则有

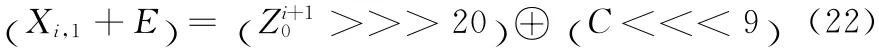
步骤2 如图5 所示，保持明文不变，在E 处注入随机比特故障m，得到新的密钥流 （）′，则有

因为Z，Z′和C 均已知，且根据文献 ［10］可以得到定理：

定理［10］对于本文2.3节中式 （8），若在X 上发生的单比特故障α，则α＝2l成立的充要条件为

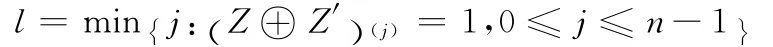
由定理1可以得到故障值m，显然式 （22）、式 （23）对应2.3节中的第一种情况，采用2.3节中的方法将其传换成二元域上代数方程组；

步骤3 重启密码设备，并保持明文不变，重新执行步骤1和步骤2，构建足够多的代数方程组；

图5 对Helix的代数故障攻击

步骤4 对步骤1～步骤3构建的代数方程系统进行求解，恢复Xi，1；

3.3 恢复密钥Xi，0

步骤1 使用3.1节明文Pi，运行密码设备得到相应的密钥流Zi＋10

步骤2 如图5 所示，保持明文不变，在G 处注入随机比特故障n，得到新的密钥流 （）′

因为由式 （19）可以计算出B 和B′，根据定理可以计算得到故障n，所以式 （24）和式 （25）同样对应于2.3节中的第一种情况，将其转换成二元域上的方程组。

步骤3 重启密码设备，并保持明文不变，重新执行步骤1和步骤2，构建足够多的代数方程组；

步骤4 对步骤1～步骤3 构建的代数方程组进行求解，恢复Xi，0；

3.4 恢复其余密钥信息

由本文1.3节Helix密钥扩展算法可知，可以对连续八轮i，i＋1，i＋2，i＋3，i＋4，i＋5，i＋6，i＋7 （其中i满足i mod8＝0）轮加密进行攻击，由于用户密钥长度（U）未知，因此由3.1节方法只能恢复工作密钥K0，K2，K3，K4，K6，K7共6个密钥，采用3.2节方法可以恢复剩下两个工作密钥K1，K5，至此恢复了Helix的全部工作密钥K0，K1，K2，K3，K4，K6，K5，K7。

4 仿真实验结果及分析

在普通PC 机 （CPU 为AMD Athlon （tm）64Processor 3000＋，内存为1G）上，使用C＋＋语言、CryptoMin－iSAT 软件实现了Helix的代数故障攻击仿真实验，其中故障诱导得到错误密文采用计算机软件模拟完成。下面给出某次Helix代数故障攻击过程：

（1）产生一个随机明文P＝21646C726F77202C6F6C6C6 54816，初始向量N＝6665646362613938373635343332313016，用户密钥U＝78696C654816，则正常运行密码设备生成的正确密文C＝0DF2232C80C5A0827AB9274C6C16；生成的工作密钥K＝39113251F5857A359FB69B734A2803F4DA15F16D20 D61C8FD2A1A3CB7AD71E6C16。

（2）根据3.1节中方法，通过选择明文P 恢复C 值；

（3）根据3.2节中方法，注入随机故障恢复Xi，1；

（4）根据3.3节中方法，注入随机故障恢复密钥Xi，0

（5）根据密钥扩展算法恢复其余密钥信息，结果见表2。

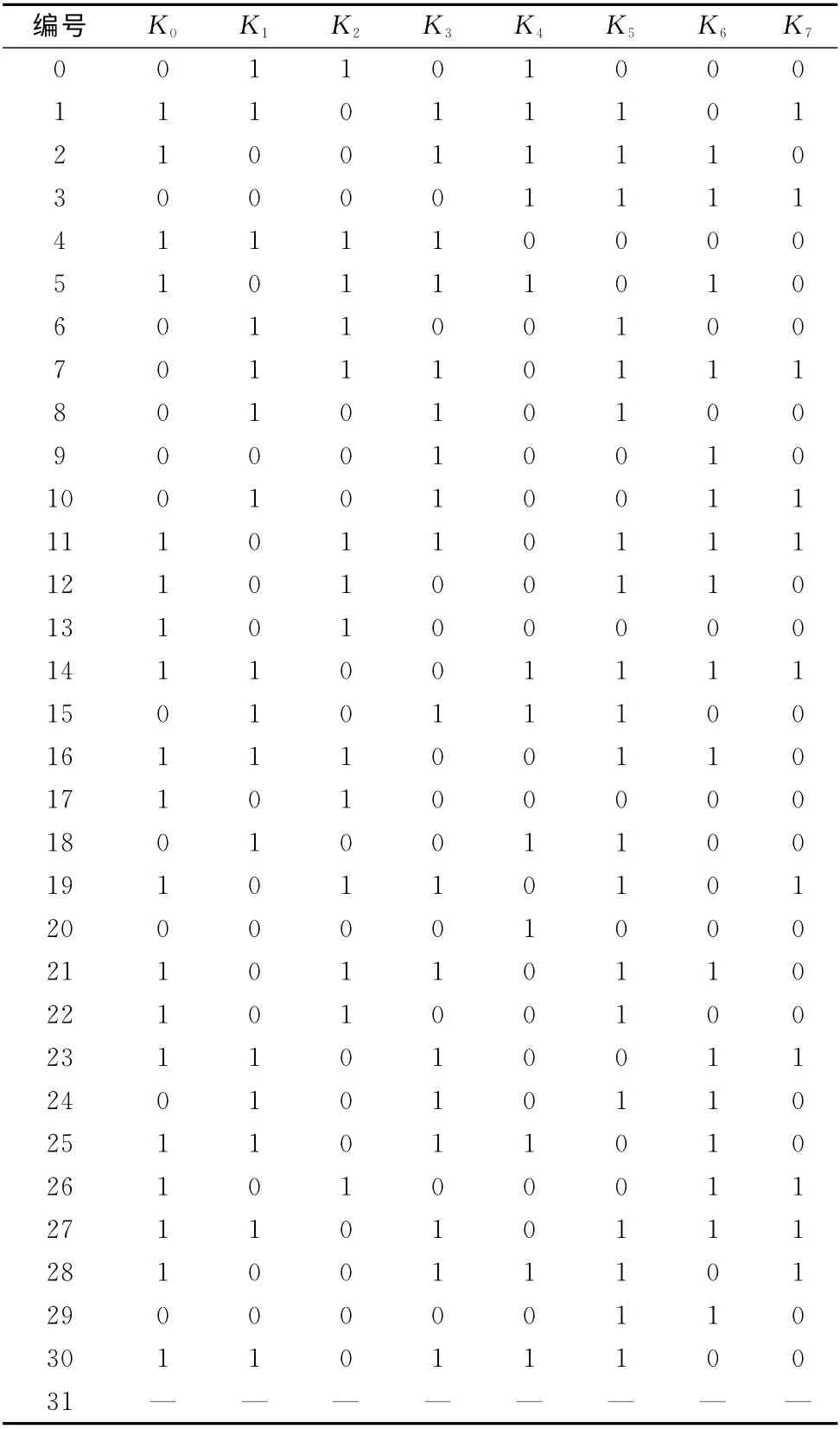
表2 Helix代数故障攻击结果

如表2所示，攻击可以恢复工作密钥K0～K7除最高1位的所有248比特，且实验结果同真实密钥一致，攻击成功，剩下的8比特密钥信息可以通过穷举得到。

图6表示恢复C 值，Xi，1，Xi，0所需选择明文次数和故障注入次数。结果表明，攻击恢复密钥Xi，1所需的故障注入次数较多约为260次，恢复Xi，1所需的故障注入次数较少仅需10次，而恢复C 值所需明文选择次数为100次，所以总的故障注入总数为580 （10×6＋260×2）次。

图6 实验恢复C 值，Xi，1，Xi，0结果

5 结束语

本文首次将代数故障攻击应用在Helix流密码上，提出了一种对模加运算通用的代数故障攻击模型，详细介绍了该模型下代数方程组的构建，给出了整个攻击过程。

实验结果表明，580次故障注入可以恢复Helix工作密钥除最高位的248比特信息，剩余8比特信息可以通过穷举得到。本文所提出的对模加方程的代数故障攻击模型具有通用性强，求解方便等优点，可以为其他具有模加运算结构的流密码和分组密码的代数故障攻击提供一定的参考。

［1］ZHENG B，GUAN J.Differential characteristic probability of added Key on modulo 2noperation ［J］.Journal of Electronics＆Information Technology，2009，31 （11）：2708－2712 （in Chinese）.［郑斌，关杰.“与密钥模2n加运算”的差分性质研究 ［J］.电子信息学报，2009，26 （2）：132－136.］

［2］Courtois N，Ware D，Jackson K.Fault－algebraic attacks on inner rounds of DES ［C］／／eSmart，2010：22－24.

［3］Mohamed M，Bulygin S.Using SAT solving to improve differential fault analysis of trivium［J］.International Journal Security and Its Applications，2012，6 （1）：29－37.

［4］Faure G，Nieuwenhuis R，Oliveras A，et al.SAT modulo the theory of linear arithmetic：Extract，inexact and commercial solvers［G］.LNCS 4996：SAT，2008：77－90.

［5］Yossed O，Mario K，Thomas P，et al.Side－channel analysis in the presence of errors［C］／／CHES.USA：California，2010：428－442.

［6］Sugita M，Kawazoe M，Imai H.Relation between XL algorithm and Grbner basis algorithms ［EB／OL］.http：／／eprint.iacr.org／112，2010.

［7］LI Junru，GU Dawu.Differential fault analysis on PRESENT［C］／／China Crypt，2009：3－13 （in Chinese）.［李卷孺，谷大武.PRESENT 算法的差分故障攻击 ［C］／／中国密码学会，2009：3－13.］

［8］Courtois N，Debraize B.Algebraic description and simultaneous linear approximations of addition in snow 2.0 ［C］／／ICICS，2008：328－344.

［9］LI Shenhua.Cryptanalysis of two symmetric encryption algorithms ARIA and Salsa20 ［D］.Jinan：Shandong University Doctoral Dissertation，2008：42－50 （in Chinese）.［李 申 华.对称密码算法ARIA 和Salsa20的安全性分析 ［D］.济南：山东大学博士学位论文，2008：42－50.］

［10］ZHANG Zhongya.Security analysis on block－like type stream ciphers［D］.Zhengzhou：PLA Information Engineering University Master Dissertation，2011：47－49 （in Chinese）.［张中亚.类分组型序列密码算法的安全性分析 ［D］.郑州：解放军信息工程大学硕士论文，2011：47－49.］