三铁柱磁饱和电抗器的建模与特性研究

赫志远，李光友，赵庆春

（1. 山东大学 电气工程学院，山东 济南 250061；2. 济南银河电气有限公司，山东 济南 250061）

随着现代工业的发展，电力系统的稳定、电能质量等越来越重要[1]。可控电抗器作为电压控制和无功补偿的主要元件，合理使用可以提高系统稳定、改善电能质量[2]。可控电抗器不仅在高压电网中起到抑制过电压的作用，而且在配电网中可以作为可调消弧线圈来动态补偿接地的容性电流[3]。另外，可控电抗器在电机起动等冲击电流的场合有抑制电压波动的作用，因而有着广阔的应用前景[4]。

国内外许多学者和科研机构都对可控电抗器进行了深入的研究，取得了一系列成果。但是目前关于磁饱和电抗器仿真建模的参考文献比较少。文献[5]所介绍的方法是通过磁控电抗器的电压方程和磁路方程，把复杂的耦合磁路分解为独立的5个磁路，这种思想非常值得提倡，但由于该模型针对的是四铁芯柱电抗器，其他类型电抗器不能直接使用。文献[6]中通过搭建Matlab/Simulink模型建立饱和电抗器的仿真模型，并未对磁路进行精确分解与计算，所以仿真精度不高，工程实用价值不大。文献[7]建立了三铁芯柱可控电抗器的数学和仿真模型，但仿真模型的正确性有待进一步商榷。

本文首先介绍了三铁芯柱磁饱和电抗器的本体结构和工作原理，其次利用磁路和电路的基本定律，列出了三铁芯柱磁饱和电抗器的电压方程和磁路方程，然后利用磁路分段法建立了三铁芯柱磁饱和电抗器的三段磁路仿真模型。最后在Matlab/Simulink环境下，对一台11 kV/400 kV·A的单相三铁芯柱磁饱和电抗器进行了仿真，仿真结果验证了仿真模型的正确性。

1 结构和工作原理

1.1 本体结构及接线方式

如图1所示，三铁柱磁饱和电抗器铁芯有3个铁芯柱，在左右2个铁芯柱上绕有工作绕组和控制绕组，控制绕组在内侧，工作绕组在外侧。中间铁芯柱绕组仅有工作绕组。这种结构的特点是直流控制磁通经2个边柱和上下轭构成回路。交流工作磁通则是经2个边柱、上下轭汇集到中柱构成回路[8-9]。

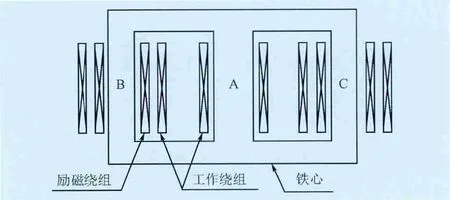
图1 电抗器铁芯结构及绕组布置Fig. 1 Iron core structure and coils arrangement of the magnetically controlled shunt reactor

如图2所示，交流工作绕组接线方式为2个边柱工作绕组并联，再与中柱工作绕组串联后与电源相接。直流控制绕组接线方式为反向串联后与控制电源相接，直流控制绕组接线反向串联可使得两绕组的工频感应电压互相抵消。对工作绕组及控制绕组电流进行傅里叶分析可知：在控制绕组中除直流电流外，还含有由交流侧感应出的一系列偶次谐波电流分量；在交流工作绕组中，除基波电流外，还含有一系列奇次谐波电流。中柱交流绕组的作用一是减少中柱上的漏磁，二是减缓控制侧对交流侧的影响。另外控制绕组所在回路中有限流电阻R和限流电抗L，限流电抗主要是为了抑制交流感应电压产生的偶次感应电流[10]。

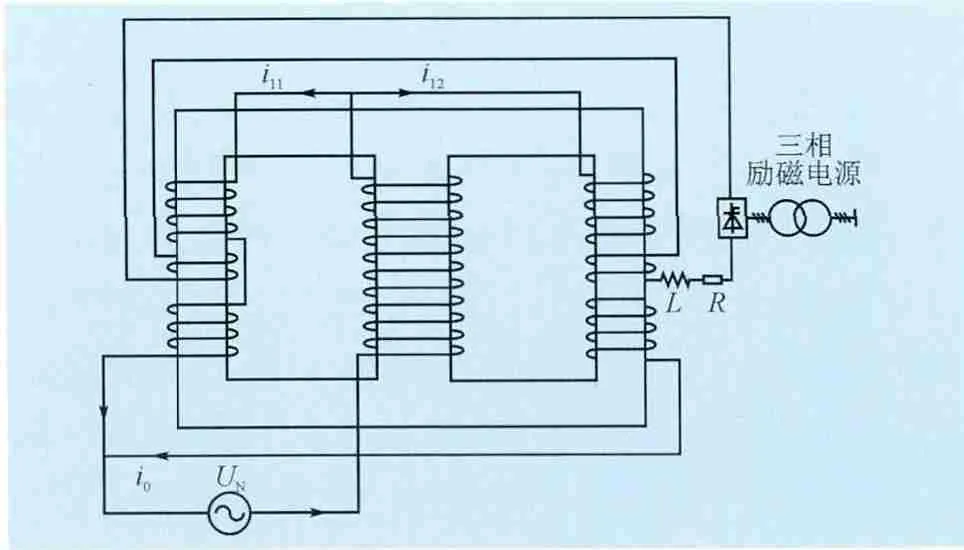
图2 电抗器的接线方式Fig. 2 Connection of the magnetically controlled shunt reactor

1.2 工作原理

铁芯电抗器的电抗为ΧL=ωΝ2Αμ/L，其中ω为角频率；Ν为绕组匝数；Α为磁路的截面积；μ为铁芯磁导率；L为磁路长度。改变直流电流可以改变铁芯的磁饱和程度，即改变铁芯的磁导率μ，从而平滑地改变电抗值[11-15]。

如图3（a），当控制电流为0时，铁芯在整个工作周期中不会饱和，铁芯等效磁导率最大，电抗器电抗值最大；如图3（b）所示，当控制电流大于0时，随着控制电流的增大，由于铁芯的非线性，在整个工作周期中一部分时间铁芯处于饱和状态，所以铁芯等效磁导率变小，电抗器电抗值变小[16]。

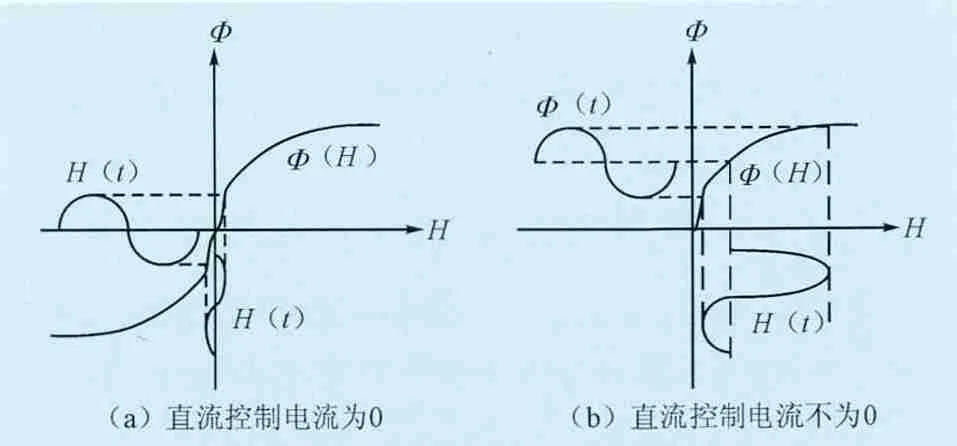
图3 铁芯Φ～H曲线Fig. 3 Relation between Φ and H in coil

2 仿真模型

2.1 数学模型

如图4所示，u1、u2分别为2个并联工作绕组的电压；u0为中柱绕组的电压；u11、u21分别为并联工作绕组电压和中柱绕组电压之和。u12、u22分别为2个控制绕组的电压。i11、i21分别为左、右边柱工作绕组电流；i12、i22分别为左、右边柱控制绕组电流；i0为中柱绕组电流。N11、N21分别为左、右边柱工作绕组匝数；N12、N22分别为左、右边柱控制绕组匝数；N0为中柱绕组匝数。对于主磁路可分为3段，其主磁通分别为Φ1、Φ2、Φ0。L11、L21分别为左、右边柱工作绕组漏电感；L12、L22分别为左、右边柱控制绕组漏电感；L0为中柱绕组的漏电感。这里需要指出的是为了便于分析，假定漏电感不随电流的变化而变化。r11、r21分别为左、右边柱工作绕组电阻；r12、r22分别为左、右边柱控制绕组电阻；r0为中柱绕组绕组的电阻。磁场强度分别为H1、H2、H0。等效磁路长度分别为l1、l2、l0。

根据电磁感应定律与基尔霍夫电压定律，可列出4个电路的电压方程：

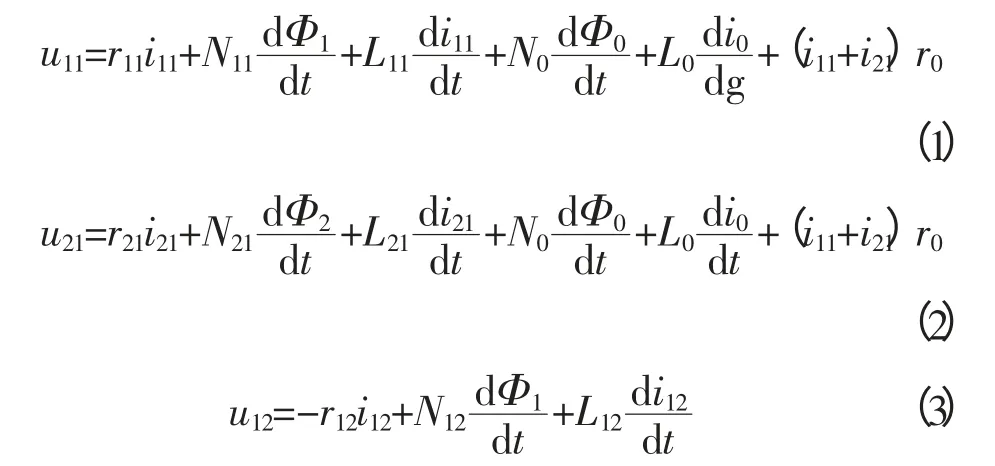
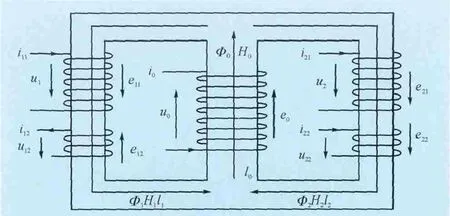
图4 电抗器各物理量及参考方向Fig. 4 Physical quantities and reference direction in themagnetically controlled shunt reactor

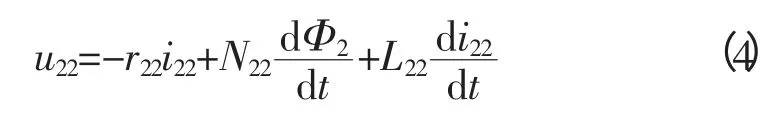
由基尔霍夫第一定律：

由基尔霍夫第二定律：

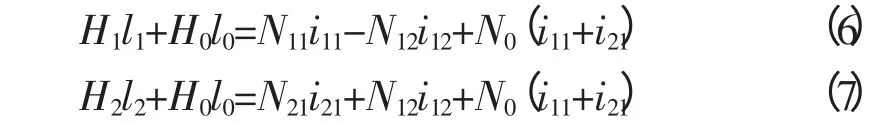
2.2 仿真模型

常规的电力仿真软件中没有电抗器的模型，本文基于磁路分解的建模方法，建立三铁芯柱磁饱和电抗器的仿真模型：

且满足以下约束条件：

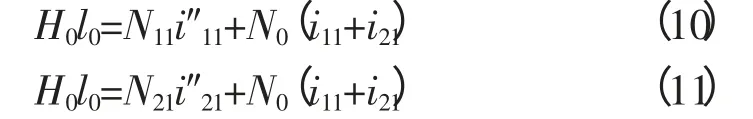
由此可以导出：

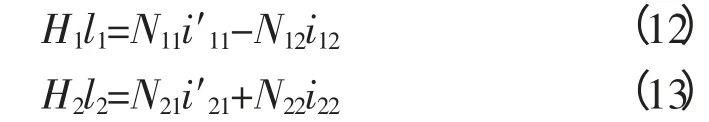
由以上电路和磁路方程，可以得到三分段磁路等效模型如图5所示。其中A、B 2个变压器是分别模磁路1、磁路2和对应的绕组；C、D、E模拟磁路0和对应的绕组，C、D为理想变压器，原副边的电流和电压相等，使E变压器铁芯中的磁通为Φ1+Φ2。因为变压器A、B、E的漏磁和绕组电阻的作用已经体现在外电路中，所以在各段铁芯磁路中只需要考虑铁芯饱和及铁损。这样将三铁芯柱磁饱和电抗器原来复杂的磁路完全由几个变压器模型进行等效，变成3个独立的磁路。

由图5可知：

式中，e11、e21、e0分别为变压器A、B、E上绕组匝数为N11时工作绕组的感应电动势。

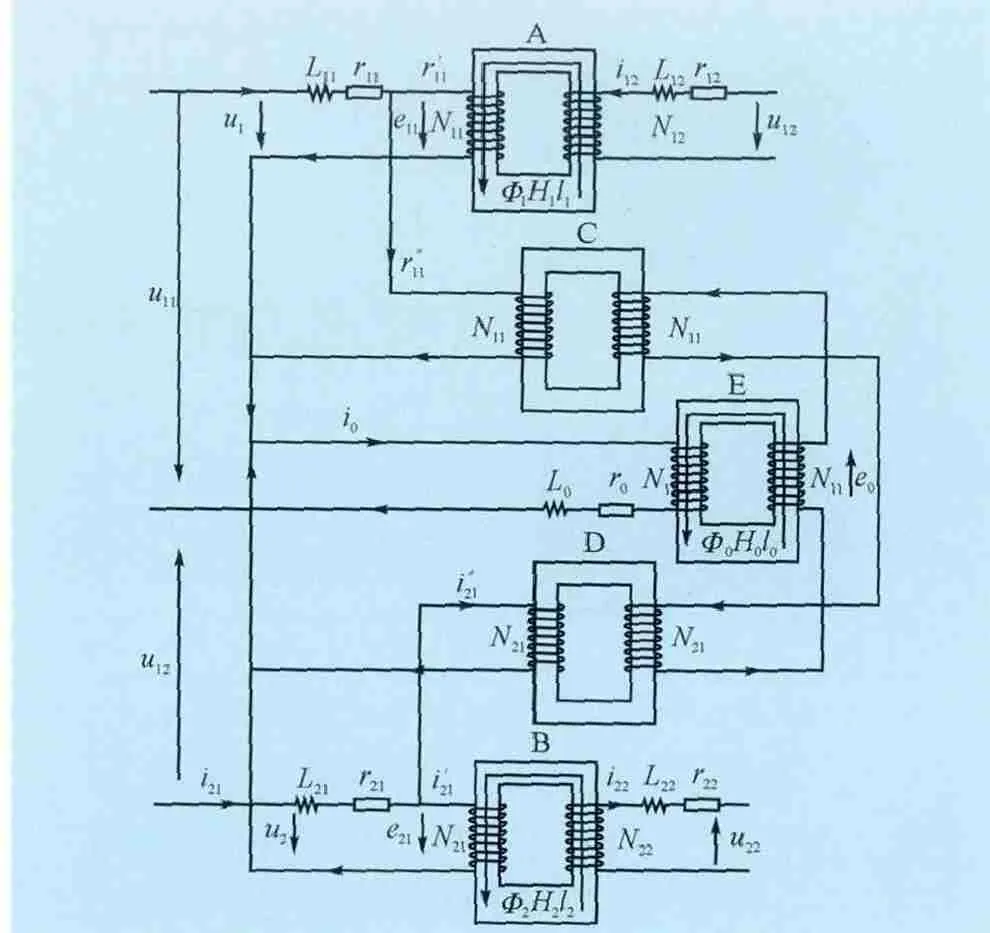
图5 电抗器三分段磁路模型Fig. 5 Three-segment magnetic path model of the magnetically controlled shunt reactor

故

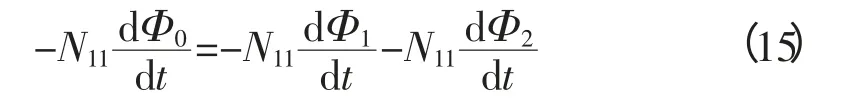
积分可得：

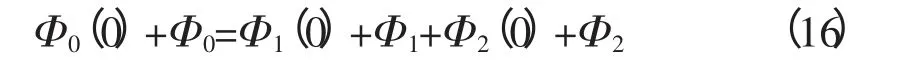
若初始磁通满足，这种磁路分段法所得到的模型就可以模拟三铁芯柱磁饱和电抗器。

3 仿真实例

样机参数如下：额定容量SN=400 kV·A，额定电压UN=11 kV，工作绕组匝数为1 040匝，控制绕组匝数为364匝，中柱绕组匝数为0匝。每柱工作绕组电阻为2.592 Ω，漏电抗为53.95 Ω。每柱控制绕组电阻为1.198 5 Ω，漏电抗为1.95 Ω。磁路l1、l2的长度为1 498 mm，磁路l0的长度为834 mm。铁芯所用材料为DQ133-30。采用Matlab/Simulink中的电力系统工具箱建立仿真模型。

3.1 电流的仿真

当控制电压为30 V时，工作绕组和控制电流的变化规率如图6所示。其中，图6（a）为工作电流的包络线，图6（b）为工作电流的有效值，图6（c）为控制电流的包络线，图6（d）为控制电流的平均值。图7为控制电压分别为10 V、20 V、30 V、40 V下，电抗器稳态工作电流随控制电压变化规律。

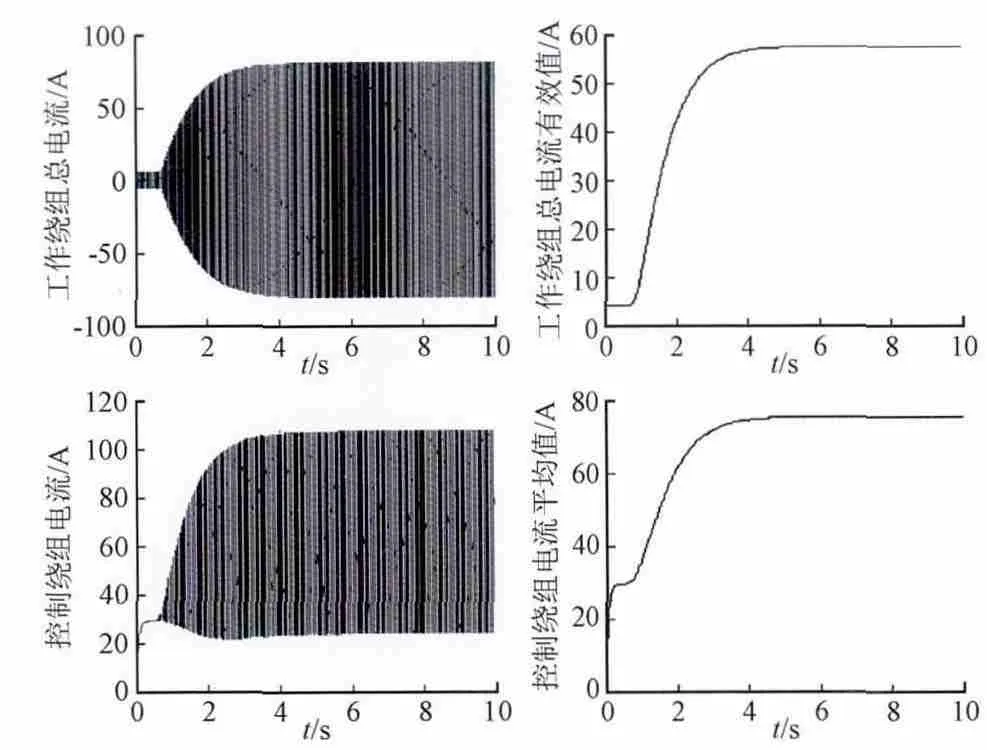
图6 控制电压30 V时的工作电流和控制电流Fig. 6 Operating current and control current under 30 V of control voltage

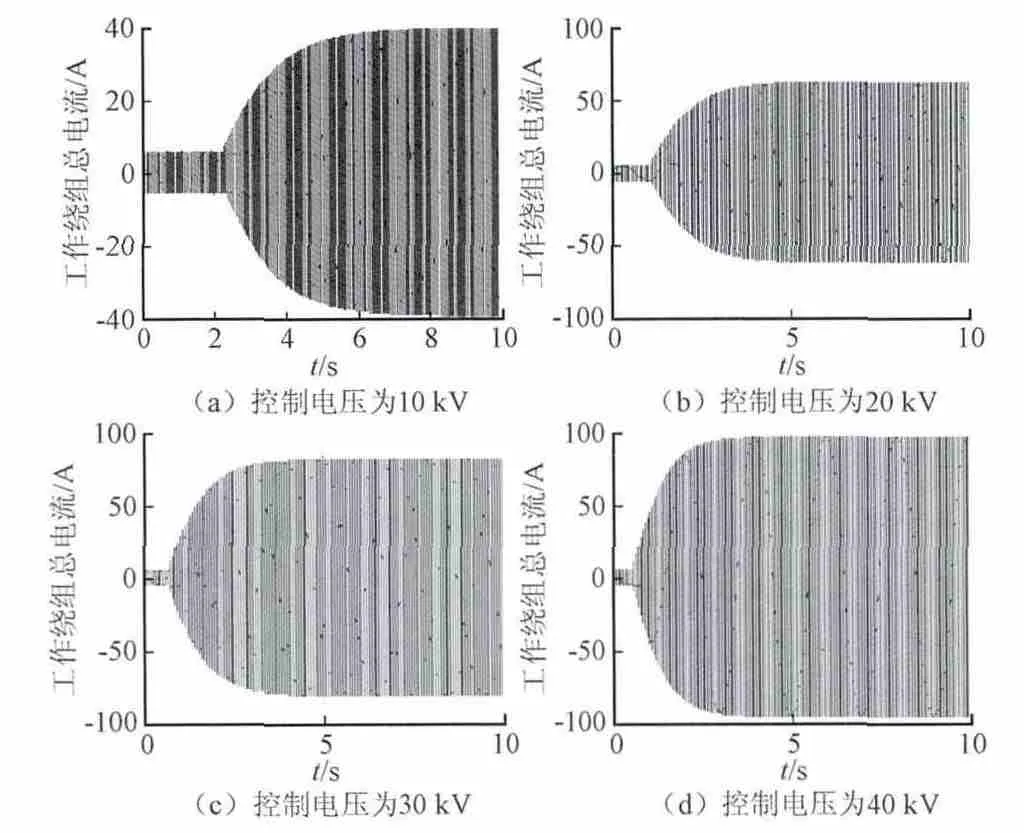
图7 工作电流随控制电压变化关系Fig. 7 Relation between operating current and control voltage

3.2 谐波特性

对不同控制电压下，电抗器稳态工作电流进行傅里叶分解，得到图8所示的5、7、11次电流谐波含量随控制电压变化规律。由此可见，5次谐波电流的最大值约为额定值的5.28%，7、11电流谐波含量小于2%额定电流。

3.3 控制特性

工作电流与控制电压的关系如图9所示，当控制电压较小时，工作电流与控制电压近似为线性关系，随着控制电压的增加，磁路饱和程度增加，当磁路完全饱和时，控制电压增加，工作电流基本不变。

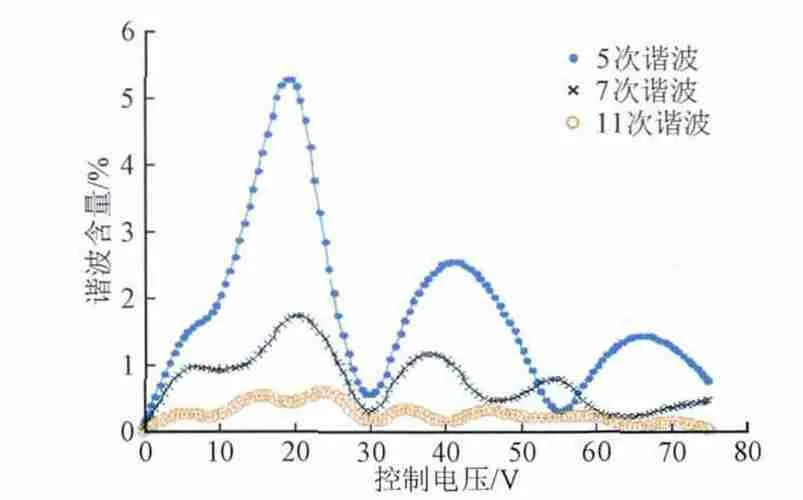
图8 谐波含量随控制电压变化关系Fig. 8 Relation between harmonic content and control voltage

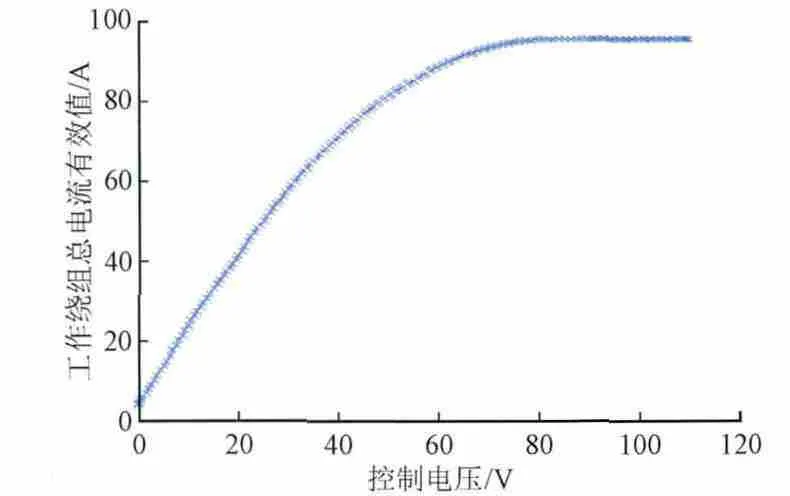
图9 电抗器的控制特性Fig. 9 Control characteristics of the magnetically controlled shunt reactor

3.4 响应时间

响应时间随控制电压的变化规律如图10所示，随着控制绕组电压的增加，响应时间逐渐变小，当控制电压增大到一定程度时，响应时间减小的速率变缓。

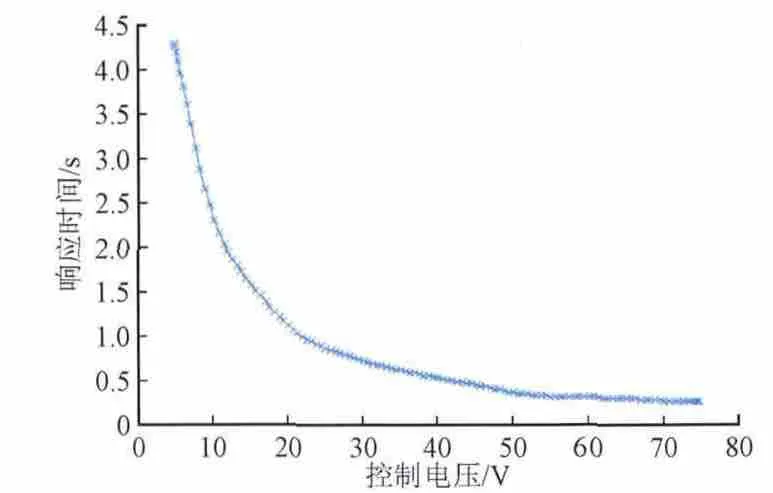
图10 电抗器的响应时间Fig. 10 Response time of the magnetically controlled shunt reactor

4 结语

针对三铁芯柱磁饱和电抗器，在建立数学模型的基础上，引入新的电流变量，将原来复杂的磁路关系分解成3个独立的磁路，建立了三铁芯柱磁饱和电抗器的三分段磁路模型。在Matlab/Simulink环境下完成了样机的仿真，仿真结果与预期相符。

利用磁路分段法建模，具有原理清晰，建模合理，仿真精确等特点，适用于电力系统电磁暂态计算，为三铁芯柱磁饱和电抗器的分析提供了必要的仿真手段。

[1] 印永华. 特高压大电网发展规划研究[J]. 电网与清洁能源，2009，25（10）：1-3.YIN Yonghua. A study of large UHV electric power grid development planning[J]. Power System and Clean Energy，2009，25（10）：1-3（in Chinese）.

[2] 周腊吾，徐勇，朱青，等. 新型可控电抗器的工作原理与选型分析[J]. 变压器，2003，40（8）：1-5.ZHOU Lawu，XU Yong，ZHU Qing，et al. Type selection analysis and principle of new controllable reactor[J]. Transfomer，2003，40（8）：1-5（in Chinese）.

[3] 陈湘，童泽，欧阳广. 磁饱和式可控电抗器的工作特性及其仿真研究[J]. 高压电器，2009，45（2）: 53-56.CHEN Xiang，TONG Ze，OUYANG Guang. Operational characteristics and simulation of the magnetic-saturated controllable reactor[J]. High Voltage Apparatus，2009，45（2）: 53-56（in Chinese）.

[4] 平孝香，刘菁. 无功补偿装置中串联电抗器的作用[J].电力电容器与无功补偿，2009，30（2）：21-24.PING Xiaoxiang， LIU Jing. The effect of series section reactor in reactive power compensation equipment[J]. Power Capacitor & Reactive Power Compensation，2009，30（2）:21-24（in Chinese）.

[5] 邓占峰，王轩，周飞，等. 超高压磁控式并联电抗器仿真模型建模方法[J]. 中国电机工程学报，2008，28（36）:108-113.DENG Zhanfeng，WANG Xuan，ZHOU Fei，et al. Modeling of extra-high voltage magnetically controlled shunt reactor[J]. Proceedings of the CSEE，2008，28（36）: 108-113（in Chinese）.

[6] 张芳，梁艳萍，章海庭，等. 磁饱和式可控电抗器的建模和仿真分析[J]. 变压器，2010，47（5）：26-29.ZHANG Fang，LIANG Yanping，ZHANG Haiting，et al.Modeling and simulation analysis of magnetic controllable saturation reactor[J].Transformer，2010，47（5）：26-29（in Chinese）.

[7] 赵世硕，尹忠东. 磁控电抗器仿真模型与实验研究[J].电气应用，2013，32（1）：52-55.ZHAO Shishuo，YIN Zhongdong. Modeling and experiment of magnetically controlled shunt reactor[J]. Electric Technology，2013，32（1）：52-55（in Chinese）.

[8] 雷园园，赵现平. ±800 kV云广直流输电工程平波电抗器参数选择和布置方案[J]. 高压电器，2012，48（6）:75-78.LEI Yuanyuan，ZHAO Xianping. Parameters selection and arrangement of smoothing reactors for ±800 kV Yunnan-Guangzhou UHVDC transmission project[J]. High Voltage Apparatus，2012，48（6）: 75-78（in Chinese）.

[9] 沈琪，汲胜昌. 合成回路用高压电抗器过电压分析及电场仿真[J]. 高压电器，2012，48（7）：31-34.SHEN Qi，JI Shengchang. Overvoltage analysis and electric field simulation of high voltage reactor in synthetic circuit[J]. High Voltage Apparatus，2012，48（7）：31-34（in Chinese）.

[10] 欧阳璋，刘全峰，梁艺超，等.干式空心电抗器工频磁场屏蔽方法的研究[J]. 电力电容器与无无功补偿，2013，34（6）: 66-73.OUYANG Zhang，LIU Quanfeng，LIANG Yichao，et al.Study on power frequency magnetic field shielding method of dry air-core reactor[J]. Power Capacitor ＆ Reactive Power Compensation，2013，34（6）: 66-73（in Chinese）.

[11] 陈柏超. 新型可控饱和电抗器理论及应用[M]. 武汉：武汉水利电力大学出版社，1999：10-18.

[12] 蔡宣三，高越农. 可控饱和电抗器原理、设计与应用[M].北京: 中国水利水电出版社，2008：1-18.

[13] 蒋琳，贺应华，王波. 磁控电抗器在调节电网电压中的应用[J]. 电力电容器与无功补偿，2013，34（1）: 36-43.JIANG Lin，HE Yinghua，WANG Bo. Application of magnetically controlled reactor to the grid voltage regulation[J].Power Capacitor ＆ Reactive Power Compensation，2013，34（1）: 36-43（in Chinese）.

[14] 程汉湘，何绍洋，黄超宪. 磁控电抗器的电磁特性分析[J]. 变压器，2013，50（8）: 16-20.CHENG Hanxiang，HE Shaoyang，HUANG Chaoxian.Electromagnetic characteristic analysis of magnetically controlled reactor[J]. Transformer，2013，50（8）: 16-20（in Chinese）.

[15] 雷娟，郭洁，高媛，等. 铁磁谐振仿真模型的探讨[J]. 电瓷避雷器，2007，4（218）：33-37.LEI Juan，GUO Jie，GAO Yuan，et al. Approach to simulation model of ferroresonance[J]. Insulators and Surge Arresters，2007，4（218）：33-37（in Chinese）.

[16] 丁冬冬. 磁控式饱和电抗器的漏电感数值计算与性能研究[D]. 哈尔滨：哈尔滨理工大学（硕士学位论文），2011:6-13.