小型化高平坦度窄步进梳状谱源研究

舒安刚，秦巍巍

(电子科技大学微电子与固体电子学院，四川成都 610054)

梳状谱发生器在现代微波系统中有着广泛的应用，通过其倍频作用可制成毫米波频率源，在仪器设备中也是展宽频带的关键，常应用于微波通信、EMC(Electro Magnetic Compatibility)测试、微波电子战等方面［1］。近年来通信行业的快速发展，高性能的接收机对高平坦度，窄频率步进的优质梳状谱的需求愈加明显。

经典的梳状谱发生器通常是以电容或电阻等非线性器件为基础，电容非线性是利用金属—半导体结电容的非线性特征，对输入信号进行非线性变换得到倍频脉冲，典型的如变容二极管等。由于电容非线性器件的结电容有较大的温度系数并对偏置电压敏感，故需要提供恒温、恒压工作条件。电阻非线性是指器件电压与电流之间具有非线性关系，双结型晶体管(BJT)、场效应管(FET)、二极管等倍频器就是利用它们的非线性电阻效应，将正弦波变成电流脉冲，产生梳状谱［2］。然而高平坦度，窄步进这些指标是常规的模拟器件所难以实现的，且模拟器件一旦确定了输入输出参数，就不易修改，而数字器件可通过编写新的程序方便灵活地进行操作，基于此，提出了基于数字器件产生梳状波的新思路。

1 数字器件产生梳状波机理

以传统的SRD倍频器件为例，SRD的工作依赖于电荷复合。如果储存的电荷在器件内保持一段比射频周期长的时间，则将产生复合，且降低器件效率。此因素决定频率的下限，在该频率，预期给定器件工作于一个令人满意的模式。频率下限以电荷寿命的倒数来定义［3］

由于电荷寿命的限制，SRD等模拟器件不适于产生低频的倍频信号。

和倍频器类似，梳状谱是由基频的谐波构成的等间隔频率信号。不管模拟器件或是数字器件，要产生具有丰富谐波的信号，就需要得到优质的周期性脉冲信号。由于文中所研究的梳状脉冲信号由脉冲电流产生，故先分析脉冲信号。

假设周期矩形脉冲信号f(t)的脉冲宽度为τ;脉冲幅度为E;重复周期为T，如图1所示。

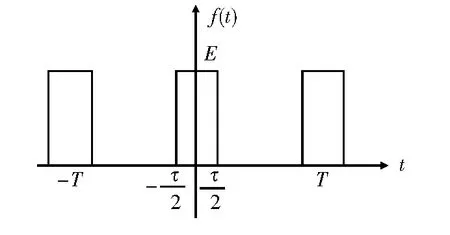
图1 周期方波信号

这种脉冲信号可表示为

对其进行傅里叶级数展开得到

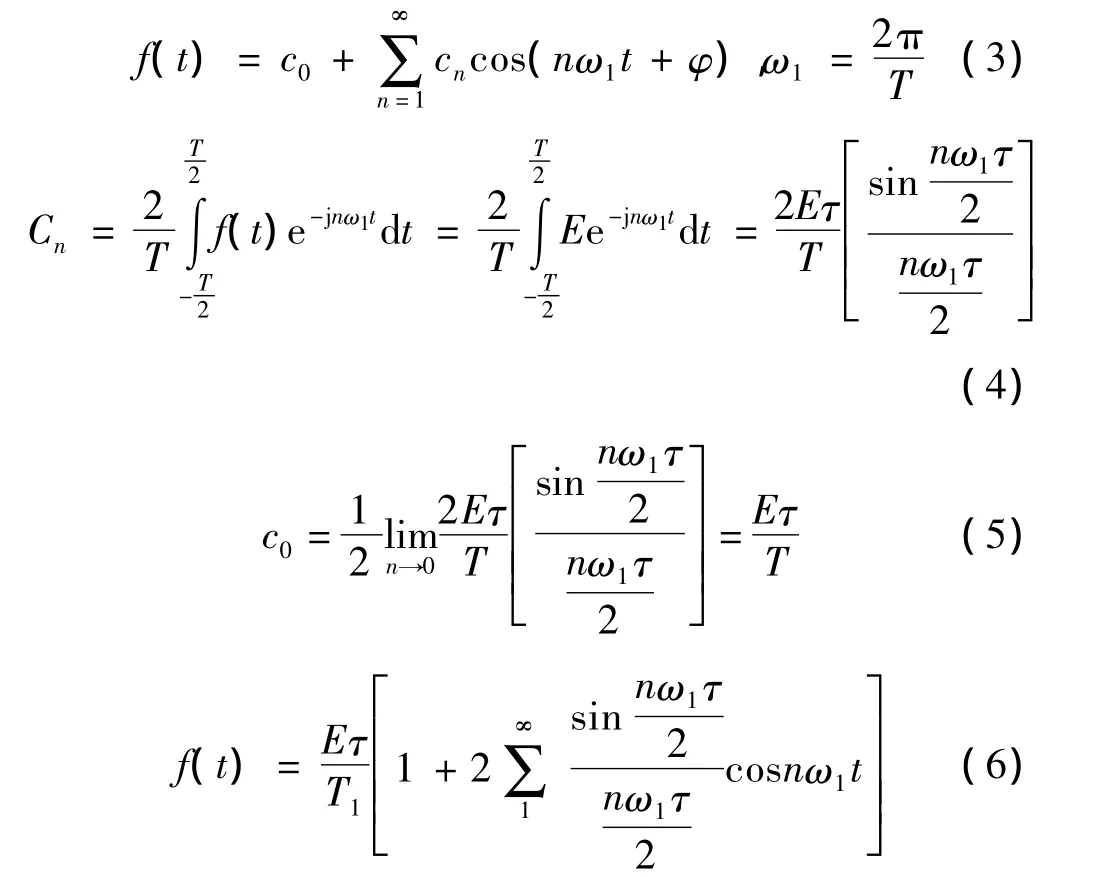
此等式是三角傅里叶级数展开式［4］，由此作出单边谱。

由复振幅的表达式可知，频谱谱线顶点的连线所构成的包络是抽样函数。根据傅里叶展开式可得频谱图如图2所示。

图2 周期方波信号频谱图像

周期方波信号频谱特点分析:(1)频谱是离散的，两谱线间的距离为基波频率ω=脉冲周期越大，谱1线越密。(2)各分量的大小与脉幅成正比，与脉宽成正比，与周期成反比。当E变大时，τ变大，则各次谐波的幅度越大;T变大，则谐波幅度越小。(3)各谱线的幅度按sin包络线变化。(4)主要能量在第一过零点内，主带宽度为

2 实验方案

实验采用Altera的一款CPLD(Complex Programmable Logic Device)作 为 计 数 器，该 CPLD 型 号 为EPM240T100C5，具有低功耗、低成本的特点，属于瞬时接通，非易失性器件，具有掉电保存功能，待机电流低至25 μA，支持高达300 MHz的内部时钟，通用IO支持 3.3 V，2.5 V，1.8 V，1.5 V 等多种电平标准［5］，是理想的计数器选择。

集成锁相环作为计数器输入时钟，锁相环和计数器的控制均由单片机进行操作。在末端用了中心频率140 MHz，带宽20 MHz的带通滤波器截取了所需的梳状谱带宽。实验方案如图3所示。

图3 实验电路方案框图

用数字计数器产生周期性方波脉冲的原理是利用计数器对输入时钟进行计数，当计数达到文中所需时间时，就产生一个时钟周期的高电平，即方波信号，然后计数器归零，进行重新计数。如图4所示，输入时钟信号200 MHz，但时钟周期为5 ns，要产生500 kHz的周期性方波信号需计数200次，且在计数器计数到200时，将输出端口置为高电平，同时将计数器清零，这样就产生了周期性方波信号［6－7］。

图4 周期方波信号产生原理

经过对周期性方波信号的分析，周期性方波信号的能量主要集中在频谱的第一个零点以内，而第一个零点取决于周期性方波信号的τ，即脉宽间隔，针对文中采用的计数器方案，就是锁相环输出给计数器的时钟信号。要得到140 MHz的高平坦度梳状波信号源，选取输入时钟应＞140 MHz，才能有更富余的频段选取空间。

在本次试验中分别选取了300 MHz，200 MHz的时钟频率进行了实验。输出频率间隔为500 kHz的梳状谱信号。在CPLD中写入如下计数器的核心代码，其中300 MHz计数次数为600次，200 MHz计数次数为400次。

always@(posedge clk_200MHz or posedge rst_n)

if(rst_n)cnt＜ =31＇b0;

else if(cnt==31＇d400)cnt＜ =31＇b0;

else cnt＜ =cnt+1＇b1;

always@(posedge clk_200MHz or posedge rst_n)

if(rst_n)fout_r＜ =1＇b0;

else if(cnt==31＇d400)fout_r＜ =1＇b1;

else fout_r＜ =1＇b0;

3 实验结果分析

按照实验方案连接好电路，在N9010频谱仪测得两组实验图像如图5和图6所示。

图5 300 MHz时钟信号，500 kHz频率步进实验图像

图5展示了输入时钟为300 MHz，计数产生频率为500 kHz方波信号的频谱图像。图5(a)为带宽设置为400 MHz，可看出频谱包络的第一个零点为300 MHz，符合理论推导谱线的幅度按包络线变化，主带宽度为。图5(b)的测试带宽为20 MHz，即图5(a)的放大，可看出频率间隔为500 kHz，与文中理论推导结果相比频谱是离散的，两谱线间的距离为基波频率相一致。

图6展示了输入时钟为200 MHz时的图像，同样图6(a)为带宽400 MHz，图6(b)为20 MHz。可以看出，谱线包络的第一零点为200 MHz，频率间隔为500 kHz。同样较好地验证了理论推导。

图6 200 MHz时钟信号，500 kHz频率步进实验图像

从以上实验结果可看到，周期性方波信号的频域谱线和经傅里叶变换求解得到单边谱一致，由于频谱仪只显示了幅度特性，因此第一个零点和第二个零点之间第二能量区的负相位不能得到体现，所有频点均为正值。文中在300 MHz和200 MHz的时钟条件下均输出了500 kHz步进的梳状频谱，表1为对比平坦度结果。

表1 实验数据平坦度

从表1中可发现，同样产生500 kHz的情况下较高的参考频率在第一零点范围内具有更高的倍频阶数，300 MHz的参考输入在第一零点内有600次基波倍频，200 MHz的参考频率在第一零点内只有400次基波倍频。可见更高的参考频率能提供更好的梳状谱选取空间，具有更好的平坦度。实际工程使用过程中，应在数字器件的工作频率范围内尽可能地选取较大的参考频率值。

4 结束语

设计了一种新型实用化的梳状谱发生器，该频率源的核心为数字计数器。产生了140 MHz中心频率，20 MHz带宽，频率步进500 kHz，通带平坦度≤1.8 dB的优质梳状谱频信号。在实际工程中作为信号源可通过混频等方式将其搬移到更高的频段，应用前景广阔。

［1］ 张清．微波全频段低功耗梳状谱发生器研制［D］．成都:电子科技大学，2009．

［2］ 费元春．固态倍频器［M］．北京:高等教育出版社，1985．

［3］ 张广显，白锡巍．阶跃二极管高阶倍频器研制［J］．半导体情报，2000，37(2):50 －52．

［4］ 何子述．信号与系统［M］．北京:高等教育出版社，2007．

［5］ Altera公司．MAX II device handbook［M］．Sanjose:Altera公司，2009．

［6］ 聂杨，喻志远．基于阶跃二极管的平面结构梳状谱发生器设计［J］．电子测量技术，2009，32(12):7 －9．

［7］ 夏莹，周勃．非线性传输线梳状谱发生器的设计［J］．科学技术与工程，2010，10(36):9094 －9098．