斜坡堤越浪量影响因素的数值研究

郭立栋，孙大鹏，黄明汉，左卫广

（1.中交第一航务工程局有限公司，天津 300461；2.大连理工大学海岸和近海工程国家重点实验室，辽宁 大连116024；3.中交天津港湾工程研究院有限公司，中国交建海岸工程水动力重点实验室，天津 300222）

0 引言

斜坡堤作为一种近岸防护型结构物在近海工程中得到了普遍应用。当波浪传播到斜坡堤时会产生显著变形，并在斜坡上破碎，给斜坡带来局部集中的动水压力和底流，当波浪较大时，堤顶还会出现越浪现象。越浪通常采用越浪量作为评价、计量及控制的参数。

越浪时波浪会不断地冲击堤顶，使得防波堤遭受破坏，严重时会形成溃堤，对堤后居民的生命财产及工农业设施造成无法估量的损失。因此，越浪量是衡量斜坡堤安全性及有效性的重要指标。同时，越浪也是波浪水动力问题的一个难点，原因在于其形成过程受到多种强非线性现象的作用，例如，波浪翻卷、破碎、冲击等。此外，对越浪量有影响的物理因素也非常多。因此，开展斜坡堤越浪研究具有非常重要的学术意义与工程价值。

最初，学者们使用模型实验对近海工程中出现的越浪进行研究，并给出相应的越浪量公式，例如：Van der Meer和 Jenssen[1]、Hebsgaard 等[2]。通过物模实验，可以获得直观、可靠的结果，但是这种方式投资大，周期长，并受到工况的限制以及模型比尺效应的影响。

目前，越浪的理论研究成果还比较少，且大部分数值计算是依托Fluent平台，例如：王鹏等[3]、刘亚男等[4]。对于越浪的数值模拟结果，大多关注的是越浪过程中波面和越浪量变化，而对越浪量影响因素尚没有形成系统研究。因此，本文采用0-1BEM+VOF[5]耦合模型对越浪量进行系统分析，具体研究了斜坡堤断面形式（胸墙高度、平台超高、平台宽度、外堤坡度）与波浪要素（波陡、相对水深）等因素对越浪量的影响。

1 数值模型

0-1BEM+VOF模型[5]是一种新型的波浪耦合数值模型。该模型是以BEM方法与VOF方法的数值特点为基础，前域采用0-1BEM模型模拟造波以及波浪的传播、变形，后域模拟波浪与结构物的相互作用则采用的是雷诺时均VOF湍流模型。0-1BEM+VOF模型的计算精度、计算效率、存储效率以及模型适用性均要优于VOF方法，同时发挥了VOF方法在自由表面追踪上的优势，并且特别适用于大范围波动场的计算。

由图1所示，模型中与越浪量有关的物理因素为：堤前水深d、波长L、波高H、堤顶到静水位高度（胸墙高度）Hc、平台标高Hr、平台宽度B，外侧坡度m。

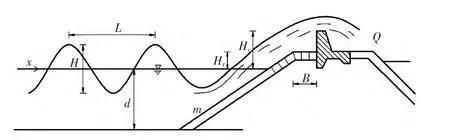
入射波采用规则波，越浪量的关系式为：

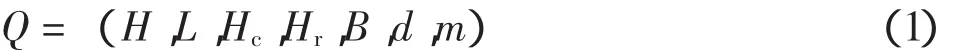
式中：Q是单个波通过单宽堤顶的流量。

为便于统计分析单宽越浪量，计算单个波浪的波峰体积A：

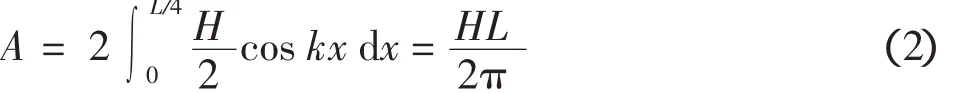
那么，越浪量可由下式表示：

式中：μ是越浪量系数。

以物模实验的经验公式[6]为依据，通过式（1）和（3）的联立，进而得到越浪量系数的无因次关系式：

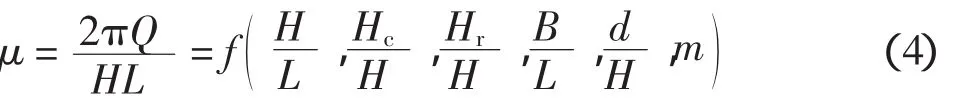
探讨公式（4）括号中的6个无因次变量，这里应用二变量关系式法，以Hc/H作为基本变量（考虑到胸墙高度的重要性），其它变量作为次变量，关系式为：

式中：x是式（4）的其它变量中的任一变量。

由文献 [5]所得结论：较合理的耦合域位置是距离结构物0.8 L~1.2 L处；较合理的耦合域长度为LTD=0.1 L~0.25 L。所以，本文在越浪计算时，将耦合域取在距离斜坡堤堤脚0.8 L处，耦合域的长度取为0.2 L。将贺朝敖[6]的实验结果作为本文计算结果的比对分析对象，并以此为基础，探讨上述各物理因素对越浪量的影响。

2 越浪量影响因素的数值分析

2.1 胸墙高度

胸墙高度是越浪量的关键影响因素，所以首先分析胸墙高度与越浪量之间的关系。具体方法为其它变量条件固定，计算不同Hc/H时的越浪量。其它变量条件：H/L=1/20，d/H=3.1，B/L=0.05，Hr/H=0，m=1.5。由于此时的H/L，d/H，B/L，Hr/H，m均为常数，故式（5） 中的越浪量系数仅是关于Hc/H的函数，即：

图2是μ-Hc/H关系曲线。虚线是由实验所拟合的经验公式值。

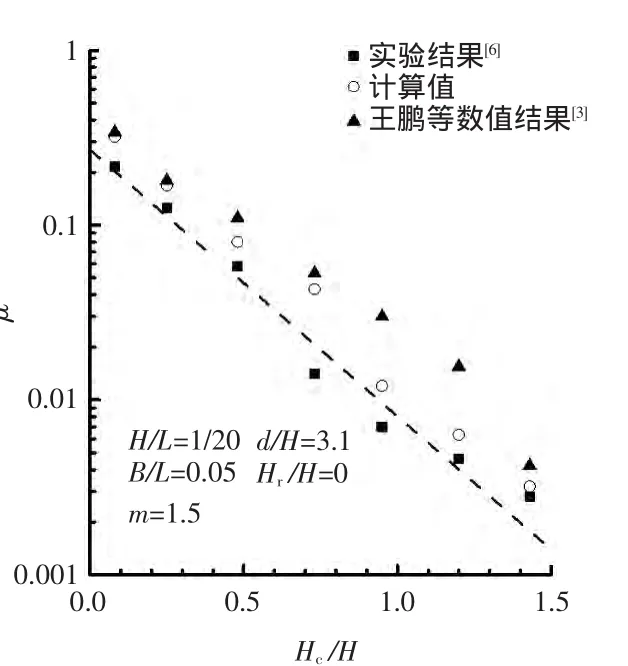
图2 μ-H c/H关系曲线Fig.2 μ-H c/H relation curve

由图2可知：所有点都位于对数坐标的1条直线附近，且离散性比较小；计算结果较实验结果略大，整体吻合度比较高；相比王鹏等[3]的计算值，本文的计算值更接近实验值，尤其在相对胸墙高度Hc/H较大时；μ和Hc/H存在指数反比关系，随着Hc/H加大，越浪量系数逐渐减小。

2.2 平台超高

分析平台超高与越浪量之间的关系。具体方法为其它变量固定，计算不同Hr/H时的越浪量。3组平台超高Hr/H=-0.5，0，0.5，负号代表在水面以下。其它变量条件：H/L=1/20，d/H=3.1，B/L=0.05，m=1.5。将实验值（实心）、实验拟合经验公式（虚线）与本文计算值（空心）绘制在图3中。由图3可见，计算结果较实验结果略大，整体吻合度比较高；Hr/H不同时，越浪量同Hc/H存在半对数的线性关系，其斜率k（参考图中虚线）与Hr/H成正比，Hr/H较大时，斜率k也较大；随着相对平台超高Hr/H加大，越浪量系数减小。

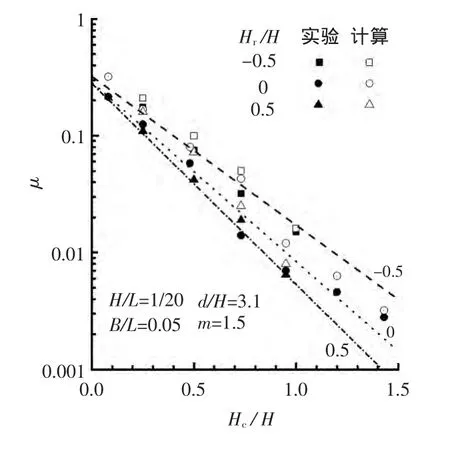
图3 μ-H r/H关系曲线Fig.3 μ-H r/H relation curve

2.3 平台宽度

分析平台宽度与越浪量之间的关系。具体方法为其它变量固定，计算不同B/L时的越浪量。4组平台宽度为B/L=0，0.05，0.11，0.16。其它变量条件：H/L=1/20，d/H=3.1，Hr/H=0，m=1.5。将实验值（实心）、实验拟合的经验公式值（虚线）与本文计算值（空心）绘制在图4中。由图4可见，计算结果较实验结果略大，整体吻合度比较高；B/L不同时，越浪量同Hc/H也存在半对数的线性关系，其斜率k（参考图中虚线）与B/L成正比，B/L较大时，斜率k也较大；随着相对平台宽度B/L加大，越浪量系数减小。

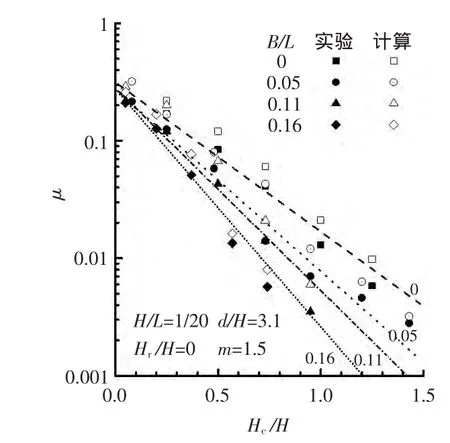
图4 μ-B/L关系曲线Fig.4 μ-B/L relation curve

2.4 波陡

分析波陡与越浪量之间的关系。具体方法为其它变量固定，计算不同H/L时的越浪量。3组波陡为H/L=1/30，1/20，1/15。其它变量条件：B/L=0.05，d/H=3.1，Hr/H=0，m=1.5。将实验值（实心）、实验拟合的经验公式值（虚线）与本文计算值（空心）绘制在图5中。由图5可见，计算结果较实验值略大，整体吻合度比较高；H/L不同时，越浪量同Hc/H也存在半对数的线性关系，其斜率k（参考图中虚线）与H/L成正比，H/L较大时，斜率k也较大；随着H/L加大，越浪量系数减小。

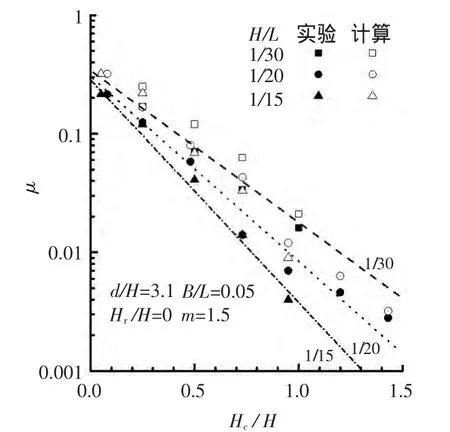
图5 μ-H/L关系曲线Fig.5 μ-H/L relation curve

2.5 相对水深

分析相对水深与越浪量之间的关系。具体方法为其它变量固定，计算不同d/H时的越浪量。3组相对水深为d/H=2.4，3.4，4.4。其它变量条件：H/L=1/20，B/L=0.04，Hr/H=0，m=1.5。将实验值（实心）、实验拟合的经验公式值（虚线）与本文计算值（空心）绘制在图6中。由图6可见，计算结果较实验值略大，整体吻合度比较高；d/H不同时，越浪量同d/H也存在半对数的线性关系，其斜率k（参考图中虚线）与d/H成正比，d/H较大时，斜率k也较大；随着d/H加大，越浪量系数减小。

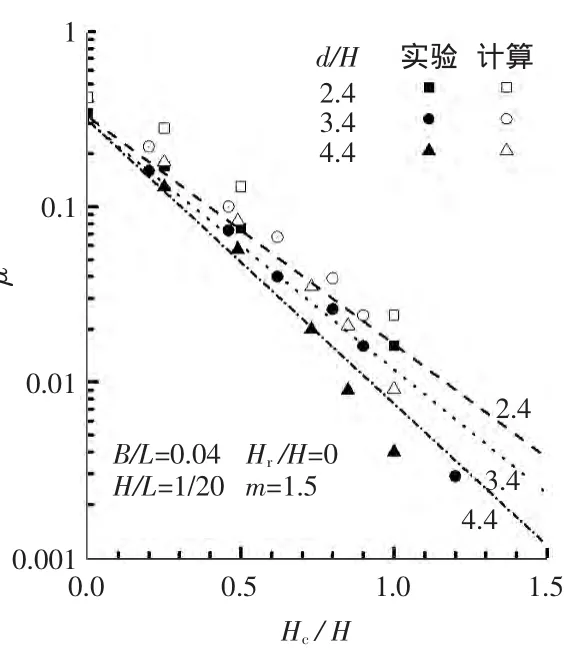
图6 μ-d/H关系曲线Fig.6 μ-d/H relation curve

2.6 外堤坡度

分析外堤坡度m与越浪量系数之间的关系。具体方法为其它变量固定，计算不同m时的越浪量。其它变量条件：d/H=3.2，B/L=0.01，Hr/H=0，Hc/H=1，2 组波陡 H/L=1/20，1/30。故式（5） 中的越浪量系数仅是关于坡度m的函数。图7是上述工况下的越浪量实验值与计算结果，可知μ与m具有线性关系。

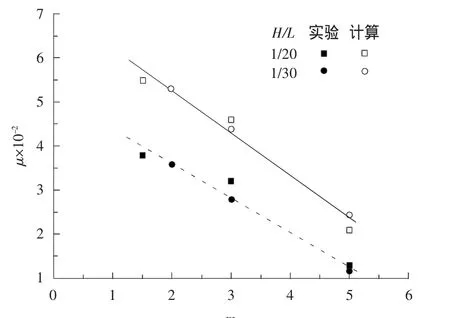
图7 μ-m关系曲线Fig.7 μ-m relation curve

3 越浪量系数的控制分析

统计分析越浪量系数的实验结果与计算结果，并将相同工况下的计算值与实验值的比值（计算值/实验值）绘制在图8中，图中两条线分别为y=1.3x和y=x。由图可见，大多数点均包含在两条线内，这表明了计算结果较实验值偏大，且偏差是可控的（30%）。本文分析计算结果偏大的原因为：1）差分格式的VOF。网格划分时，差分格式VOF方法在斜坡上进行了简化处理，它不具备强大的地形适应能力；2）越浪机理的复杂性。实际上VOF方法对破碎、水汽掺混等强非线性现象的模拟也仅是简化的处理，而相当部分的波浪在上述作用中损耗，目前该损耗值在数值计算中仍无法准确衡量，所以爬高距离、越浪量大小等数值结果均会被高估，Hsiao与Lin[7]也有类似看法；3）物理实验比尺效应。

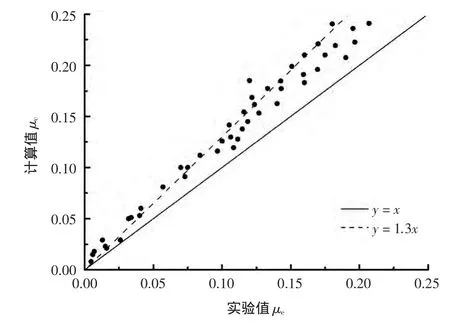
图8 实验与计算值的对比Fig.8 Comparison of fitted valuebetween measuresand calculated values

4 结语

本文采用一种新型的波浪耦合数值模型（0-1BEM+VOF模型）对斜坡堤越浪进行模拟。为了深入研究越浪量的影响因素，数据处理时应用二变量关系式的方法，选取Hc/H作为基本变量（考虑到胸墙高度的重要性），其它变量作为次变量。通过与他人实验结果的对比分析得出结论：相对胸墙高度Hc/H对越浪量系数具有十分显著的影响，它们之间存在指数反比关系；其它变量对越浪量也有一定影响，随着Hc/H的变化，变量与越浪量之间也具有指数线性关系。本文计算结果较实验值偏大但可控。

[1]VANDERMEERJW，JANSSENJPFM.Waverun-up and wave overtopping at dikes and revetments[R].Netherlands：Delft Hydraulics，1994.

[2]HEBSGAARD M，SLOTH P，JUHL J.Wave overtopping of rubble mound breakwaters[C]//Proceedingsof theinternational conference on coastal engineering.2011，1（26）：2 235-2 248.

[3] 王鹏，孙大鹏.基于FLUENT的海堤越浪数值模拟[J].中国水运：下半月，2011（7）：73-75.WANG Peng，SUN Da-peng.Numerical simulation of wave overtopping over seawalls based on FLUENT[J].China Water Transport：thesecond half of themonth，2011（7）：73-75.

[4] 刘亚男，郭晓宇，王本龙，等.基于RANS方程的海堤越浪数值模拟[J].水动力学研究与进展：A 辑，2007，22（6）：682-688.LIU Ya-nan，GUOXiao-yu，WANGBen-long，et al.Numerical simulation of wave overtopping over seawalls using the RANS equations[J].Journal of Hydrodynamics：series A，2007，22（6）：682-688.

[5] GUO Li-dong，SUN Da-peng，WU Hao.A new numerical wave flume combiningthe 0-1 type BEM and the VOF method[J].Journal of Hydrodynamics，2012，24（4）：506-517.

[6] 贺朝敖，任佐皋.带胸墙斜坡堤越波量的试验研究[J].海洋工程，1995，13（2）：62-70.HE Chao-ao，RENZuo-gao.Experimental study on wave overtopping of rubble mound breakwater with vertical wall[J].The Ocean Engineering，1995，13（2）：62-70.

[7] HSIAO SC，LIN T C.Tsunami-like solitary waves impinging and overtopping an impermeable seawall：experiment and RANSmodeling[J].Coastal Engineering，2010，57（1）：1-18.