基于Simulink的风机控制系统仿真平台的设计

王思铱，赵蒙莉，陈昆明

(上海电气风电设备有限公司，上海 200241)

0 引言

随着气候问题日益受到关注，风力发电技术作为可操作性最强的可再生能源技术，引起了越来越多的重视。然而和很多其他产业类似，井喷式发展更加关注生产制造而相对忽略了技术发展，这也导致了目前绝大多数的核心技术还是掌握在国外厂家的手中，风机控制系统就是其中之一。

控制系统作为整个风力发电机组运行的大脑，优秀的控制策略和控制参数能够在很大程度上降低机组的载荷，提高机组的效率和寿命。因此国外风电厂家对于控制技术都是采取封闭的措施。国内厂家也慢慢地开始开展控制系统方面的研究工作，但是和国外厂家的差距依然非常明显。因此早日掌握风机控制技术也显得越来越迫切。而对于这点，一套能够确切反映控制系统实际运行情况的仿真平台就显得尤为重要了。通过这个平台，技术人员能够设计和优化风机的控制系统，并通过该平台了解这些设计和改动对于实际机组所产生的影响，对于掌握控制的核心技术有着非常重要的意义。

1 仿真平台结构

根据风机控制系统的主要工作原理[1]，仿真平台可以分成4个模块，其结构如图1所示。风速模块用来模拟实际的风速和风向信号，叶片气动模块根据风速模块的输出，模拟叶片从风中获取能量的过程。驱动链模块主要包含了齿轮箱、发电机等主要驱动链部件。控制系统模块从其他模块获取机组仿真的数据，并通过执行机构调节机组的运行[2]。下面就根据不同的模块对整个仿真平台进行介绍。

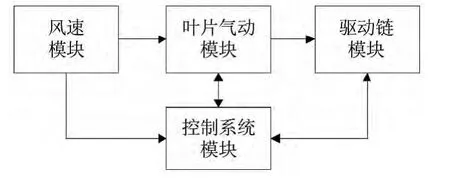
图1 仿真平台结构

1.1 风速模块

风速是风力发电系统最主要的输入条件。正确的风速模型不仅能更真实的反应实际风速变化情况，而且能够给整机的设计研究提供正确的依据。而在风速中，最重要的一个模型就是湍流。

湍流的常用模型有很多种，目前主流的载荷计算平台中，使用最多的还是Kaimal模型。参考 GL和IEC的注释[3]，Kaimal模型下，湍流的谱密度函数可通过公式(1)表示:

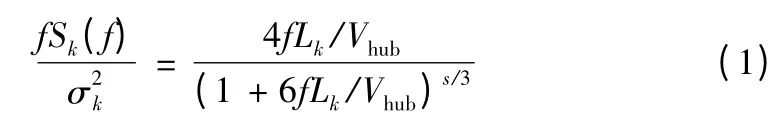
其中，f为频率，Sk(f)为湍流的普密度函数，Vhub为轮毂中心高度处的风速，σk为位于轮毂中心高度处的风速的标准差;Lk为湍流尺度参数。

图2所示的图形为根据Kaimal模型所仿真出的风速波形，其中设置平均风速 Vhub=15m/s，Iref=0.14。

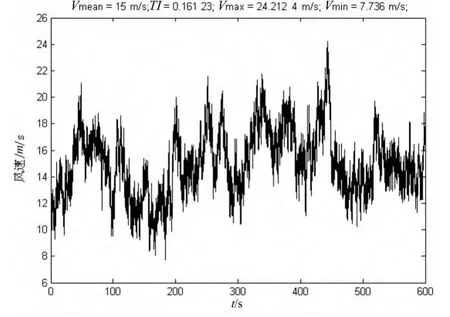
图2 通过Kaimal模型所仿真出来的风速

1.2 叶片气动模型

叶片是风力发电机的核心部件，从风中获取能量并传递给驱动链。设定机组叶片的扫风面积为A，风速为V，空气密度为ρ，则叶片可以获取的机械能量如公式(2)所示:

公式(2)中，Cp称之为风能利用系数，它用以描述叶片能够从风轮中获取到能量的多少。根据贝兹理论，理论上Cp可以达到16/27，不过对于目前的技术而言，在实际中通常只能达到0.47左右。Cp是风机设计中最重要的参数之一。对于变桨距的风机而言，Cp和叶尖速比λ和桨距角β有关系，即Cp=f(λ，β)。一个标准的Cp(λ，β)关系曲线如图3所示。

从图3中可以看出，对于不同的λ和β，Cp的值都有所不同。对于每一个固定的桨距角β值，在不同的叶尖速比下，都能对应找到一个最大值Cpmax。风机控制系统的主要工作之一，就是在最大程度上保证机组能够工作在Cpmax，从而使得机组的发电效率达到最高。

1.3 驱动链模型

驱动链包括了齿轮箱、发电机等等核心部件。主要起到传递转速和转矩的作用。在研究控制系统的响应时，只考虑其控制意义上的传递模型，一个常规的齿轮箱模型如公式(3)所示:

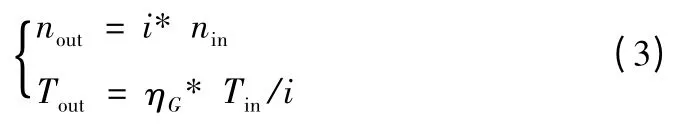
其中nin，nout为输入和输出转速，Tin，Tout为输入和输出转矩，i为传动比。ηG为传动效率。

发电机是驱动链中最重要的一个部件，控制系统通过变流器对发电机的电磁转矩进行控制，实现对发电机转速的控制。其控制模型可以通过公式 (4)表示:

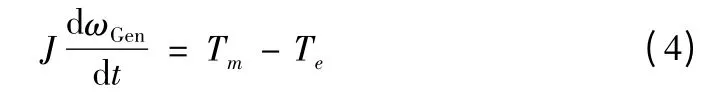
其中Tm为发电机的输入转矩;Te为发电机制动转矩;J为系统的转动惯量;ωGen为发电机转速。

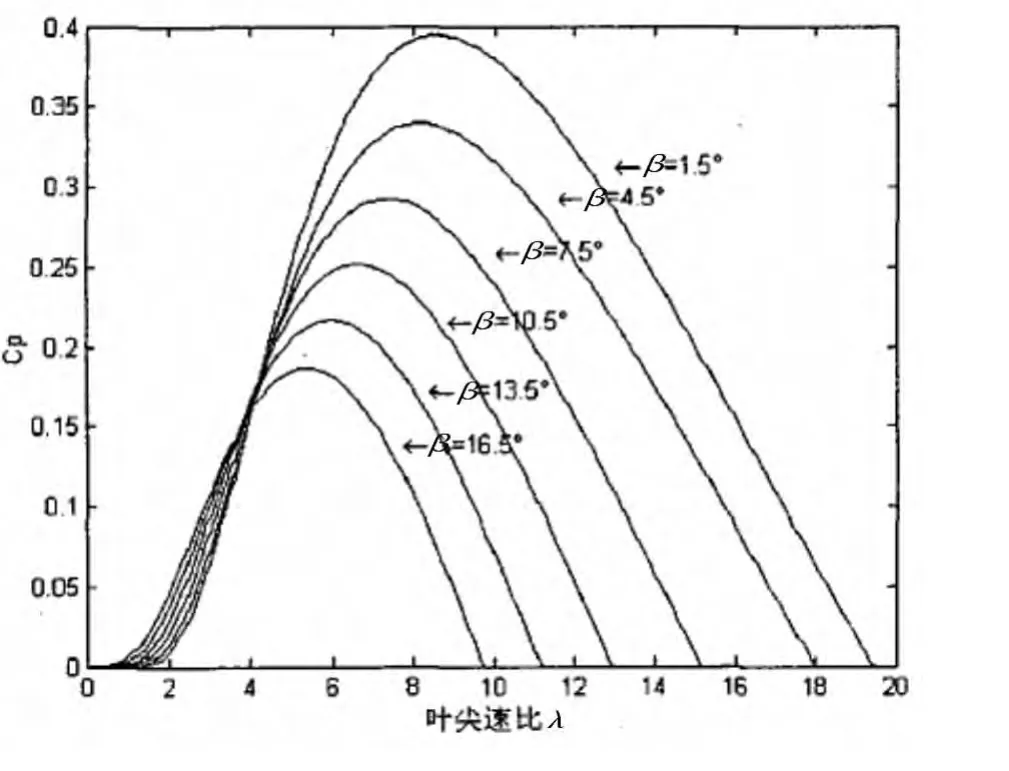
图3 Cpmax关系曲线

1.4 控制系统模型

对于变速变桨式的风力发电机组，控制系统从功能角度区分，可以分为:数据采集、控制器、执行机构这3个主要部分。其结构如图4所示。

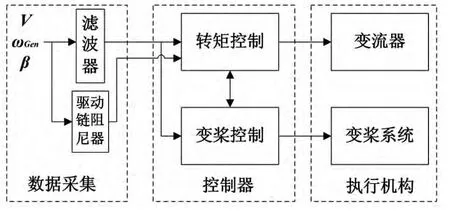
图4 控制系统结构

1.4.1 数据采集

除了常规的滤波器外，风力发电机组增加了一个特殊的滤波器，称之为驱动链阻尼器。它的主要功能是为驱动链提供额外的阻尼，用于降低驱动链的振动。驱动链阻尼器[4]的模型如公式(5)所示，其中ω为驱动链共振频率，ξ为驱动链阻尼，τ为时间常数

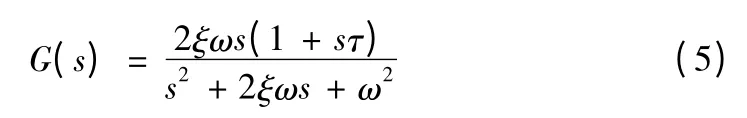
1.4.2 控制器

控制器是控制系统的主体，要实现一个风机控制器，明确其控制需求是必不可少的，一般主要包括控制策略和控制算法两个主要部分。

(1)控制策略

对于变速变桨式机组，根据发电机转速的不同，其控制策略可分成3个控制区间，如图5所示。

区间Ⅰ:在这个区间，变桨系统不启动。通过转矩控制使风机工作在最佳Cp值之下。

区间Ⅱ:在这个区间，当发电机转速低于额定转速时，通过转矩控制维持最佳Cp值的工作状态。当转速达到额定转矩之后，就需要通过控制转矩来维持转速的恒定，必要的时候需要启动变桨系统。

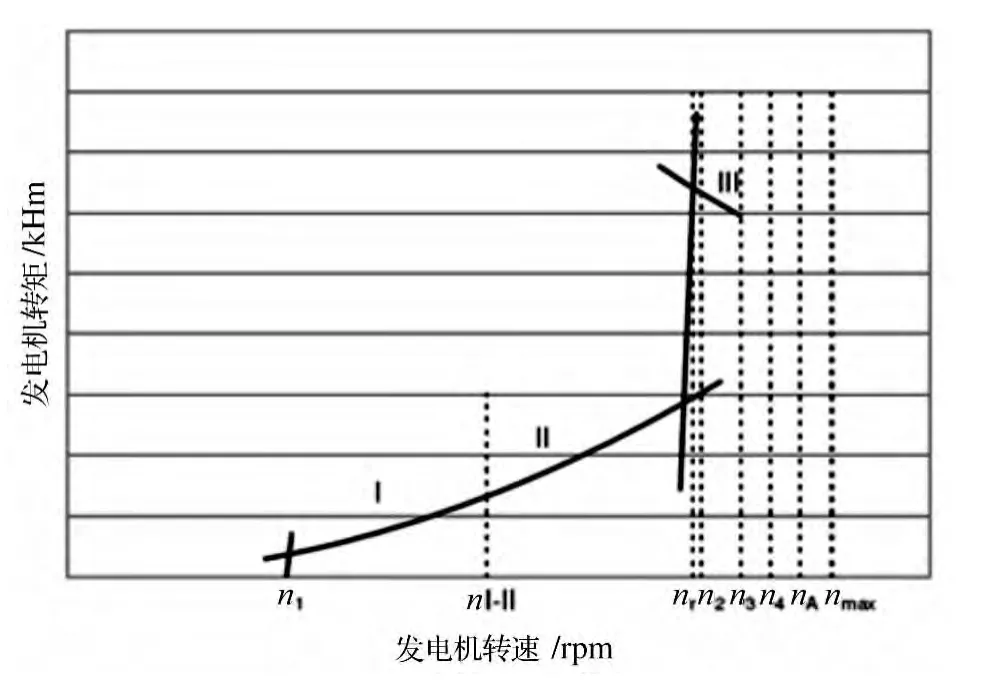
图5 变速变桨式机组控制策略图

区间Ⅲ:在这个区间，通过变桨控制维持机组的转速，通过转矩控制维持发电机的额定功率输出。

(2)控制算法

风机的控制对象和控制目标都比较明确，因此在仿真平台中选用了相对最适合的增量式PID算法[5－6]，其优点就在于每次计算的结果只是一个变化量Δy(n)，即使计算出现失误，也不会对于整体的y(n)造成严重的影响。其标准如公式(6)所示。

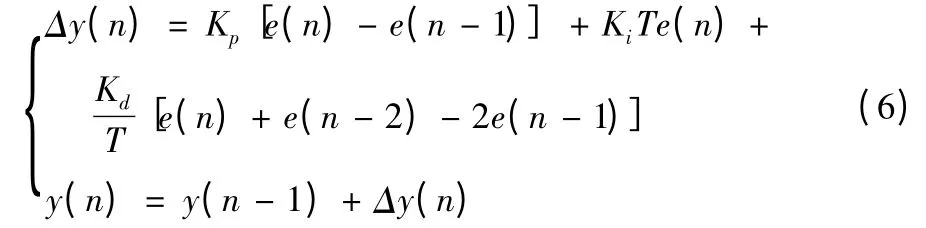
1.4.3 执行机构

执行结构主要指的就是变流器和变桨系统。对于仿真系统来说，为了简化计算过程，这两个系统可以通过一个二阶传递函数来表示，如公式(7)所示。

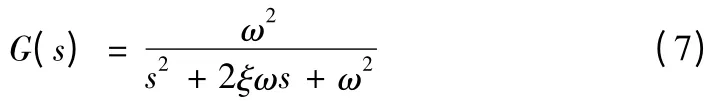
2 仿真结果比对

为了分析仿真平台的运行结果及其可行性，将仿真平台的运行结果和Bladed软件进行比较。Bladed软件是目前风电行业是使用最为广泛的设计软件之一[7]，因此具有很强的参考意义。比对结果如图6和图7所示。Bladed软件所考虑的内容更全面，采用的数学模型更加复杂，因此两者在计算结果方面不可能做到完全一致。但是对比结果分析，可以看到计算结果非常接近。表明仿真平台能够很好的反映出风机控制系统的特性。

3 结束语

仿真平台的搭建能够为以后更加深入地研究和设计控制系统提供一个相当便利的平台，不过由于国内在风机控制系统方面的技术还相对不成熟，许多技术难点还没有掌握，例如独立变桨、塔架频率控制等等。这就需要技术人员投入更多的时间和精力来攻克。而风机的仿真技术也在不断的更新，如何能够更好地为设计人员提供技术上的支持，例如增加机械载荷计算等等，也需要在未来的工作中进一步进行研究。

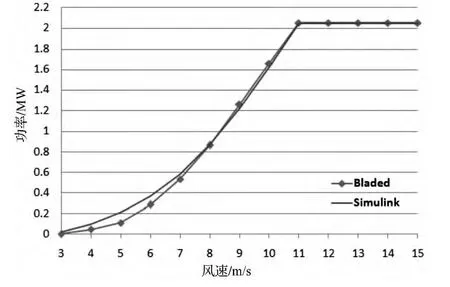
图6 静态功率曲线比对

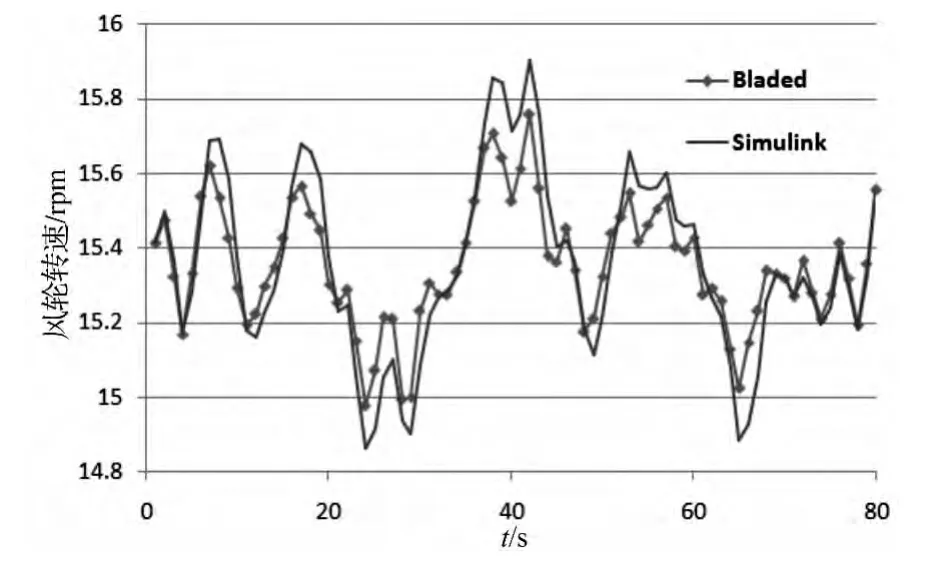
图7 动态控制响应

[1]Tony Burton，David Sharpe，Nick Jenkins.Wind Energy Handbook[M].England.JOHN WILEY ＆ SONS，LTD.，2001.

[2]D.A.J.Wouters，T.G.van Engelen.Modern wind turbine controller design[R].Netherlands.The Energy Research Center of the Netherlands ECN.2008

[3]IEC 61400 － 1，Wind turbines-Part 1:Design requirements[S].IEC，2010.

[4]E.Muljadi，C.P.Butterfield.Pitch-Controlled Variable Speed Wind Turbine Generation[R].USA.National Renewable Energy Laboratory.2000

[5]谢赐戬.基于 Bladed的大型风力发电机组控制器优化设计[D].沈阳.沈阳工业大学，2008:17－27.

[6]卢奭瑄.风力发电机组动力模型及循环变桨控制策略研究[D].沈阳.沈阳工业大学，2012:42－46.

[7]Garrad Hassan.Bladed Theory Manual[M].England.Garrad Hassan ＆ Partners Ltd.2010