网纹红土分级加载与分别加载蠕变试验研究

何玉荣，李建中

(中南大学地球科学与物理信息学院，湖南长沙 410083)

网纹红土是在第四纪更新世湿热气候下原地表浅层粘土经过风化成壤作用而产生的堆积物，它具有红白相间的网纹结构。网纹红土在我国南方特别是长江中下游地区的低缓丘陵、阶地、山间盆地和部分山麓地带分布广泛。

有学者已对网纹红土的工程地质特性进行了研究［1～3］，研究表明网纹红土具有土质坚实致密、压缩性低，抗水性强、土体强度高等特性。近期的研究则表明网纹红土具有明显的蠕变特性，是一种弹、粘、塑性的综合体［4～7］。这种特性直接影响以网纹红土为持力层的各类构筑物的长期稳定性。因此，对网纹红土的蠕变特性进行系统深入地研究是预测和控制构筑物基础的长期沉降、维护构筑物的稳定以确保构筑物长期安全的关键所在［8］。

粘性土的蠕变特性可以通过蠕变试验进行研究［9～11］。蠕变试验加载方式有分级加载和分别加载［12］。分级加载是采用一个土样，逐级施加不同的荷载。分别加载是采用一组土样，施加恒定的荷载，不同土样可以施加不同的荷载。分级加载试验要求的时间长，由于土样硬化，上一级荷载对下一级荷载产生影响。由于一组土样的性质很难完全相同、试验设备以及试验环境很难完全一致，分别加载的试验结果具有较大的离散性，但因它不受加载状态的影响，其试验结果较分级加载更符合工程实际情况。

目前，国内外学者大多是采用分级加载的方式进行蠕变研究。为了利用分级加载蠕变推算分别加载蠕变，本文对网纹红土未扰动样分别进行了分级加载条件下与分别加载条件下的单向固结蠕变试验，对两种加载条件下的试验结果进行了分析，并将两种加载条件下的蠕变特性进行了对比研究，进一步得出了它们之间的相关性。

1 叠加原理

图1是两种加载条件下的蠕变曲线。分级加载蠕变曲线呈梯级发展，分别加载蠕变曲线是以0时刻为起点的一簇曲线。基于应用叠加原理［13］(图2)，可以将分级加载蠕变曲线进行水平平移，得到与分别加载条件下相似的蠕变曲线簇，这时可以对两者的蠕变特性进行对比分析，研究它们之间的相关性。

根据叠加原理(假定土样均质、各向同性)，随时间变化的荷载引起的蠕变变形等于各级应力增量的变形之和。土样在应力差σn-σ1作用的时间Tj=t-tj内变形的增量总和为:

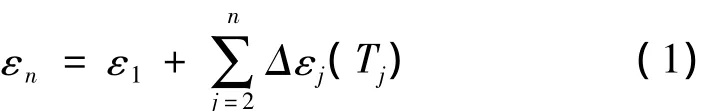
如在应力σ4作用下的变形总和为ε4=ε1+△ε2+△ε3+△ε4。

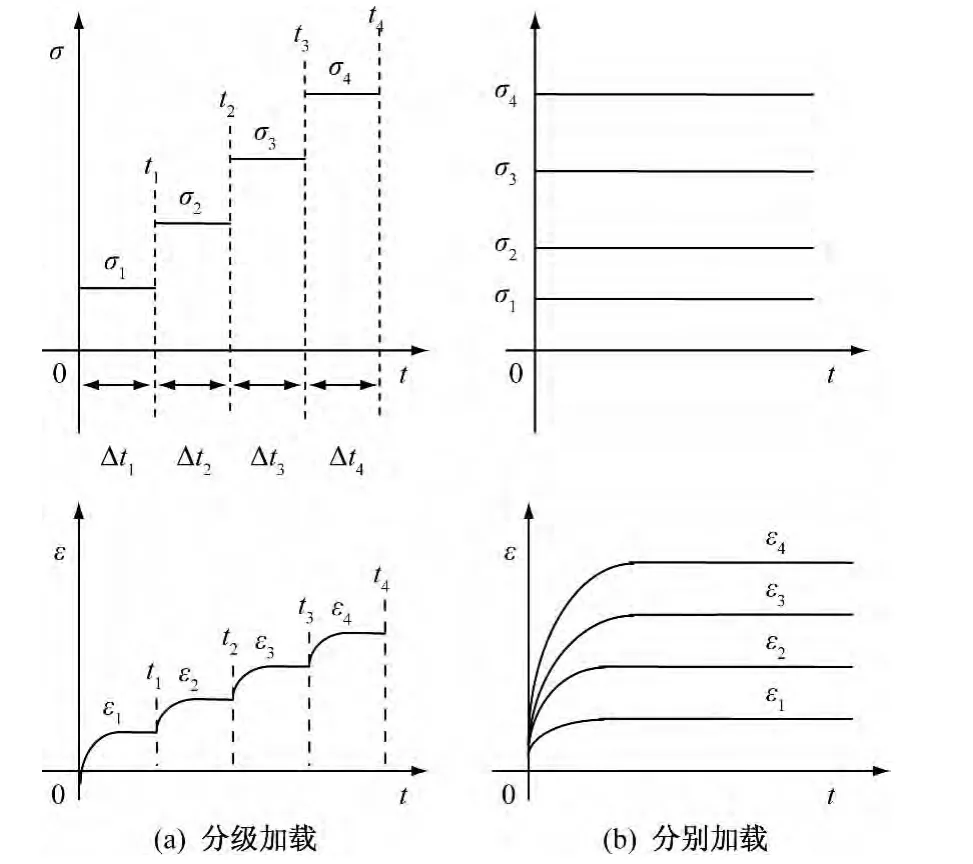
图1 蠕变曲线Fig．1 Creep curves

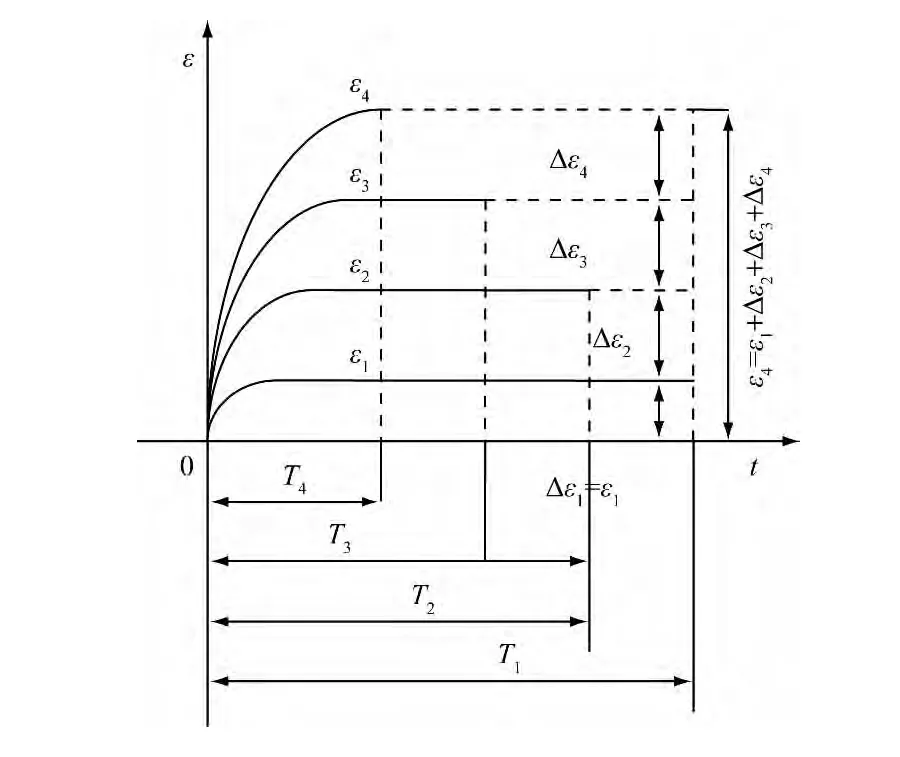
图2 叠加规律Fig．2 Superposition principle

2 试验方案

试验共采集18个网纹红土未扰动样。土样是横截面积为30cm2、高度为2cm的圆柱体，物理性质参数为:比重为2.71，天然含水率23.83% ～26.88%，天然密度1.90～1.95g/cm3。蠕变试验仪器是采用双面排水侧限的WG型三联低压固结蠕变仪(图3)。

分级加载条件下蠕变试验是指将试样装入水平台中间的固结容器后，对3个土样平行进行了初始加载—卸载—重复加载过程的单向固结蠕变试验。初始加载序列为 50kPa—100kPa—200kPa—400kPa—800kPa，卸载序列为 400kPa—200kPa—100kPa—50kPa—0kPa，重复 加 载 序 列 为 50kPa—100kPa—200kPa—400kPa—800ka。分别加载条件下蠕变试验是指将将试样装入水平台中间的固结容器后，对5组土样进行了不同应力水平(50kPa，100kPa，200kPa，400kPa，800kPa)下初始加载—卸载—重复加载过程的单向固结蠕变试验，同一组的3个试样进行平行试验。

图3 固结蠕变仪Fig．3 Oedometer

本文以变形小于0.005mm/24h为变形达到稳定的标准。两种蠕变试验都是土样在上一级荷载作用下变形达到稳定以后，再对其施加下一级的荷载。为了降低偶然误差，将3个土样进行了平行试验，试验结果取3个土样的算术平均值。

3 蠕变试验结果与分析

图4是分级加载条件下与分别加载条件下蠕变应变与试验时间的关系。从图4中可以看出:①分级加载条件下的初始加载、卸载、重复加载过程中，变形随试验时间增加呈现梯级变化;②分别加载条件下，初始加载、卸载、重复加载每个过程的荷载施加后变形会迅速增加并随试验时间最终趋于稳定。

基于叠加原理，以每级荷载加载起始时刻为该级荷载蠕变初始时间，图4可以分别转化为图5、图6。

从图5、图6中可以看出:土样在初始加载、卸载、重复加载过程中的每级荷载下都有明显蠕变变形发生，变形随蠕变时间t增加而明显增加;初始加载过程中，除第一级荷载情况外，其他各级荷载下分级加载蠕变明显小于分别加载蠕变;卸载过程中，在卸下每级荷载后土样都会保留不可恢复的变形;重复加载过程中的蠕变较初始加载过程中的蠕变明显要小。

为了研究网纹红土蠕变规律，将图5与图6中的曲线进行转化。以蠕变时间t与应变ε*的比值为纵坐标，蠕变时间t为横坐标，得到分级加载条件下和分别加载条件下t/ε*-t的关系(图7、图8)。

从图7和图8中可以看出，无论是在分级加载条件下还是在分别加载条件下，初始加载、卸载、重复加载过程中的每级荷载作用下的t/ε*-t的关系曲线都近似一条直线。即:

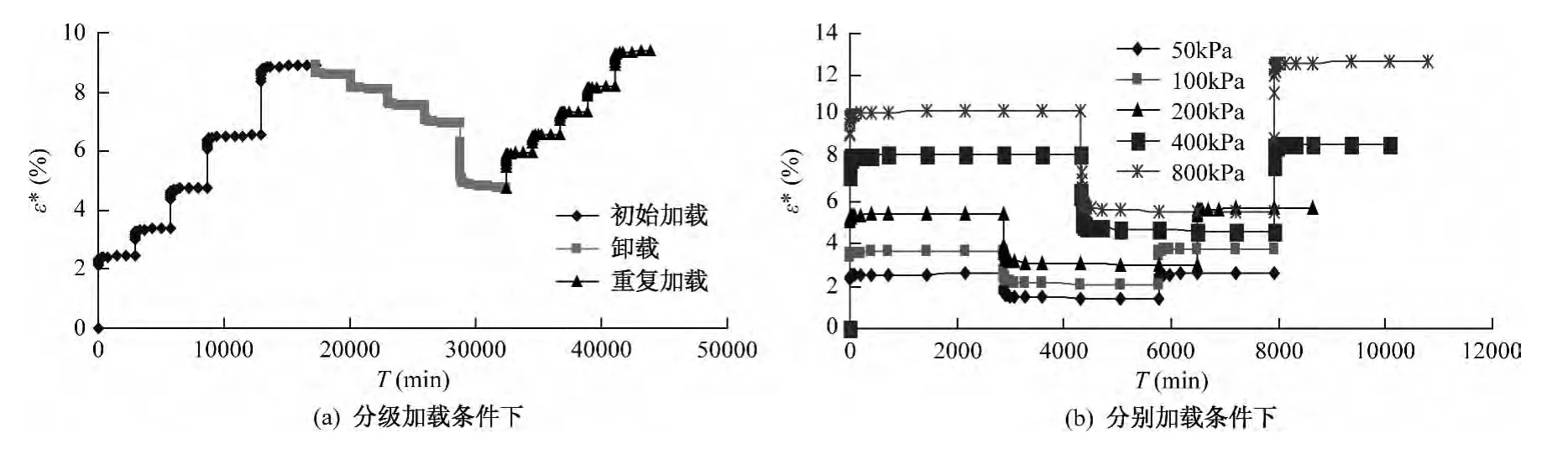
图4 不同加载条件下的蠕变应变-试验时间曲线Fig．4 Curves of creep strain-test time under different load conditions

图5 分级加载条件下蠕变曲线Fig．5 Creep curves under stepped-load

图6 分别加载条件下蠕变曲线Fig．6 Creep curves under constant-load

图7 分级加载条件下t/ε*-t的关系Fig．7 Relationships between t/ε*and t under stepped-load

图8 分别加载条件下t/ε*-t的关系Fig．8 Relationships between t/ε*and t under constant-load

式中:ε*——试样的蠕变应变算术平均值，即 ε*=(ε1+ε2+ε3)/3;

t——以每级荷载加载起始时刻为该级荷载蠕变初始时间而计算时间;

a，b——t/ε*-t线性关系的斜率和截距。

计算公式(2)的线性相关系数，发现两种加载条件下t/ε*-t线性相关系数均大于0.99，表明两种加载条件下t/ε*-t的线性关系都非常密切。将公式(2)进行转化，可以得到网纹红土的蠕变经验方程:

根据公式(3)可以计算网纹红土在任意时刻的蠕变变形。

当t→∞时，公式(3)可以转化为:

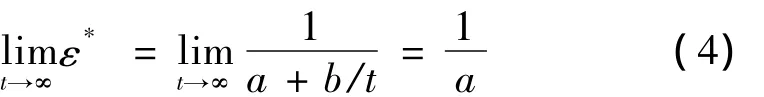
式(4)表明通过t/ε*-t线性关系的斜率可以预测各级荷载作用下蠕变的最终稳定值。表1、表2中分别列出了分级加载条件下与分别加载条件下t/ε*-t线性关系的a、b以及最终应变预测值1/a。

从表1、表2中可以发现，在分级加载条件下与分级加载条件下的各级应力水平下，根据蠕变经验方程计算得到的蠕变最终稳定值与蠕变试验测得的最终稳定值非常接近。

以分级加载条件下的t/ε*-t线性关系式的斜率(ac)为纵坐标，以分别加载条件下t/ε*-t线性关系式的斜率(as)为横坐标，得到图9中的各散点。

表1 分级加载条件下各参数值Table 1 Parameters of stepped-load

表2 分别加载条件下各参数值Table 2 Parameters of constant-load

图9 不同试验过程中as-ac关系理论计算值与拟合值Fig．9 Comparison of theoretical calculated and fitted as-acin different test stages

图9中各点几乎排列在一条倾斜的直线上，即:

式中:ac，as——分别加载和分级加载条件下 t/ε*-t线性关系的斜率;

c，d——ac与as线性关系的斜率和截距。

计算得到的ac与as的线性相关系数均大于0.9，表明ac与as线性关系密切。线性回归得到的c，d如表3所示。

将表3中的c，d值代入公式(5)中，绘出ac与as关系的拟合直线，如图9中的直线所示。从图9中可以看出在初始加载、卸载、重复加载的每个过程中，ac与as的线性关系都拟合得较好。

表3 公式(5)中的斜率和截距Table 3 Slope and intercept of Equation(5)

根据公式(4)，当t→∞时，

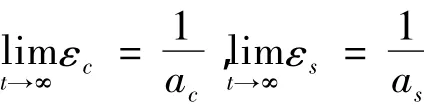
联合公式(5)可以得到:

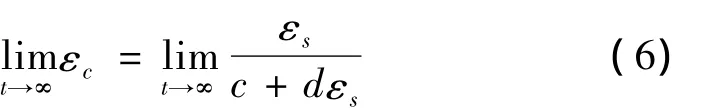
式中:εc，εs——分别加载和分级加载下的蠕变应变。

根据公式(6)可以由分级加载蠕变的最终稳定值推算分别加载的最终稳定应变值。

图10是分别加载条件下，初始加载、卸载、重复加载过程中不同蠕变应力下的实测蠕变最终变形稳定值与根据式(6)计算得到的最终变形稳定值的对比图。

图10 分级加载条件下的不同应力水平下最终应变实测值与推测值的对比Fig．10 Comparison of theoretical and calculated ultimate strain under different stress under constant-load

从图10中可以看出分别加载条件下的不同蠕变应力下的最终应变的计算值与实测值很接近。因此，可以根据分级加载条件下的最终蠕变值推算出分别加载条件下的最终蠕变值。

4 结论及展望

(1)分析网纹红土在分级加载和分别加载条件下的蠕变曲线，发现网纹红土未扰动样在分级加载与分别加载条件下的初始加载、卸载、重复加载每个过程中的每级应力作用下都有明显蠕变变形发生，蠕变随应力的增加而明显增加，蠕变与应力水平有关。

(2)网纹红土未扰动样的蠕变时间与蠕变应变的比值跟蠕变时间(t/ε*-t)存在线性关系，通过网纹红土蠕变经验方程可以预测蠕变变形的发展。

(3)对比分析网纹红土在分级加载和分别加载条件下的蠕变试验结果，发现分级加载条件下t/ε*-t线性关系的斜率与分别加载条件下t/ε*-t线性关系的斜率(ac与as)也存在线性关系。

(4)研究表明利用分级加载的蠕变变形稳定值可以较好地推算出分别加载的蠕变变形稳定值。

本文中研究的方法还处于初步阶段，还有以下几个方面需进一步的研究:

(1)要推算出网纹红土在分别加载条件下任一时刻的蠕变，还需要研究出分级加载蠕变经验方程中的b值与分别加载蠕变经验方程中的b值之间的关系式，即 bc=f(bs)。

(2)为了提高推算方法可靠度和实用性，需要考虑应力因素，研究应力水平对这种推算影响，即得出ac=f(as，σ)。

［1］ 谢俊文.湖南网纹红土的工程地质特性［J］.环境化学，1982(2):5-7.［XIE J W.Geological characteristics of reticulate red clay of Hunan［J］.Environmental Chemistry，1982(2):5-7.(in Chinese)］

［2］ 向春尧.网纹红土的工程地质特性和地基评价［J］. 水文地质工程地质，1985，12(3):1-8.［XIANG C R. Geological characteristics and foundation evaluation of reticulate red clay［J］.Hydrogeology＆ Engineering Geology，1985，12(3):1-8.(in Chinese)］

［3］ 王清，唐大雄.我国南方中更新世网纹红土的工程地质评价［J］.工程地质学报，2000，8(增 1):330-333.［WANG Q，TANG D X.Foundation evaluation of reticulate red clay of the Middle Pleistocene in south China［J］.Journal of Engineering Geology，2000，8(s1):330-333.(in Chinese)］

［4］ 唐喜青，李建中，晏露超，网纹红土剪切试验研究［J］，山西建筑，2009，35(22):3-5.［The shear experimental study of reticulated red clay［J］.Shanxi Architecture，2009，35(22):3-5.(in Chinese)］

［5］ 晏露超，李建中，唐喜青.洞庭湖地区典型网纹红土的单轴固结实验研究［J］.岩土工程技术，2009(6):276-283.［YAN L C，LI J Z，TANG X Q.Research on uniaxial consolidation test of the typical reticulate red clay around Dongting Lake area［J］.Geotechnical engineering technique，2009(6):276-283.(in Chinese)］

［6］ LI J Z，YAN L C，TANG X Q.Simulation on the onedimensional consolidating deformation of reticulate red clay［C］.The 2nd InternationalSymposium on Information Engineering and Electronic Commerce，Ternopil，Ukraine，2010:86-89.

［7］ LI J Z，TANG X Q，YAN L C.Simulation on triaxial compression creep deformation of reticulate red clay［J］.Advanced Materials Research，2011，261(4):1414-1418.

［8］ 李建中，彭芳乐.黏土的蠕变特性试验研究［J］.岩土力学，2006，27(2):214-218.［LI J Z，PENG F L.Research on creep property of clay［J］.Rock and Soil Mechanics，2006，27(2):214-218.(in Chinese)］

［9］ 王松鹤，骆亚生，杨静敬.原状黄土固结蠕变特性试验研究［J］.水文地质工程地质，2009，36(6):72-75.［WANG H S，LUO Y S，YANG J J.Experimental study on creep consolidation behavior of intact loess［J］.Hydrogeology ＆ Engineering Geology，2009，36(6):72-75.(in Chinese)］

［10］ 何利军，孔令伟，张先伟. 湛江软粘土蠕变特性及经验模型［J］. 水文地质工程地质， 2011， 38( 1) : 59 -64. ［HE L J，KONG L W，ZHANG X W. Creep properties and empirical model of soft clay in Zhanjiang［J］. Hydrogeology ＆ Engineering Geology，2011， 38( 1) : 59 - 64. ( in Chinese) ］

［11］ 李鹏，刘建.不同含水率软弱结构面剪切蠕变试验及模型研究［J］.水文地质工程地质，2009，36(6):49-53.［LI P，LIU J.Experimental and theoretical studies on the effects of water content on shear creep behavior of weak structural plane of sandstone［J］.Hydrogeology ＆ Engineering Geology，2009，36(6):49-53.(in Chinese)］

［12］ C.C.维亚洛夫.土力学的流变原理［M］.北京:科学 出 版 社，1987.［Vyalov S S. Rheological fundamentals of soil mechanics［M］.Beijing:Science Press，1987.(in Chinese)］

［13］ 范广勤.岩土工程流变力学［M］.北京:煤炭工业出版社，1993.［FAN G Q.Rheological mechanics in geotechnical engineering［M］.Beijing:China Coal Industry Publishing House，1993.(in Chinese)］