基于同步大地电磁时间序列依赖关系的噪声处理
王辉,魏文博,3,金胜,3,叶高峰,3,景建恩,张乐天,董浩,李波,谢成良
1 中国地质大学(北京)地球物理与信息技术学院,北京 100083
2 地质过程与矿产资源国家重点实验室,北京 100083
3 地下信息探测技术与仪器教育部重点实验室,北京 100083
1 引言
大地电磁测深(Magnetotellurics,简称 MT)是一种通过研究天然电磁场的传播规律来探测地下介质电性结构的勘探方法(Cagniard,1953).方法提出之初,由于受微弱天然场信号高精度采集技术的限制,发展缓慢.20世纪90年代随着科技的快速发展,MT仪器设备有了很大发展(魏文博,2002),如今,MT已经成为研究区域断裂构造(谢成良等,2012)、流体运动(Wei et al.,2001;Bai et al.,2010),以及板块构造和大陆动力学(金胜等,2012;张乐天等,2012)等问题的重要地球物理方法之一.
通常认为大地电磁测深的高频信号主要来自于雷电等中高空天气活动,低频则来自太阳风与地球磁层的相互作用,这些场源距地球很远;当它传播到达地球表面时,可以认为基本满足平面波场的理论条件,而其他不满足平面波场条件的电磁场信号,则是MT的干扰噪声(Junge,1996).实际上,大地电磁测深(MT)的实测数据必然包含了大地电磁场信号和噪声.因此,如何从受干扰的信号中求取精确的MT阻抗张量是通过大地电磁测深数据反演获取较准确的地下介质电性结构模型的关键.尽管最小二乘法可以有效去除高斯随机噪声;但对于实测数据而言,噪声却往往是非高斯分布的情况,因而利用常规的最小二乘算法通常很难得到理想的结果.为此,1986年Egbert和Booker在最小二乘法的基础上提出了Robust估计.Robust的实质是离差加权估计,在统计过程中对离差大的数据给予较小的权,离差小的数据给予较大的权,从而使曲线连续圆滑,剔除“飞点”,但对输入端的磁场噪声无能为力.1978年Gamble等提出远参考技术,基于一定距离内同步信号相关而噪声不相关的原理,抑制不相关噪声,得到阻抗的无偏估计.随着卫星同步采集技术的成熟,远参考技术得到了广泛应用,该方法对不相关的磁场噪声抑制效果明显,但会增大误差棒(Gamble et al.,1979b);实际应用中我们发现,对于电场噪声和低频噪声的处理效果不佳,还存在参考距的影响等问题(Shalivahan and Bhattacharya,2002).加拿大PHEONIX公司的处理系统,通过人工挑选,删除受干扰时段的功率谱,提高MT响应数据的质量,但处理过程非常耗时,处理人员须具有一定经验.随着我国工业化进程日益加快,人文电磁噪声对大地电磁场的干扰日趋严重;在某些经济发达地区,微弱的MT信号几乎被强干扰噪声淹没(汤井田等,2012b),尤其当MT电场信号受到强相关噪声的干扰时,传统的MT数据处理方法得不到令人满意的处理结果.
在传统MT信号处理方法中,时频转换是以傅里叶变换(FFT)为基础的技术,而FFT主要用于对“平稳信号”的变换;但MT信号具有较强的“非平稳性”,针对MT信号非平稳性的特点(王书明和王家映,2004),近些年来,更多处理“非平稳”信号的方法被引入到MT数据处理中,如小波变换(Wavelet)、希尔伯特-黄变换(HHT)和广义S变换.小波变换的优点在于对信号局部特征的分析,可以有效抑制随机噪声和局部相关噪声,但小波变换的处理效果依赖于母波的选取(徐义贤和王家映,2000;Daniel and Travassos,2000).HHT的优点是自适应性和时频分析能力,其最小二乘法处理结果与FFT经Robust估计的结果相当,显示出了优越的噪声处理潜力(Chen et al.,2012),缺点在于对信号进行经验模态分解时,窗口的首尾端会引入误差,而且分解速度慢,实用性不强(蔡剑华,2010).广义S变换是一种优于小波变换的时频分析方法,在时频谱中分析噪声,可以改善低频段数据质量,但窗函数易引起边缘效应(景建恩等,2012).
在时域中对时间序列进行预处理,直接滤除强干扰噪声,可以防止短时间的强干扰噪声影响到频域中的多个频点甚至整个频带的信号质量.时域大地电磁场的噪声处理方法主要有:人工神经网络滤波、Kalman滤波、经验模态分解(EMD)、形态滤波以及IARWR.人工神经网络滤波利用神经网络的学习和自适应功能,对数据进行分类,区分噪声与信号,分类的正确性与训练网络时的输入信号和噪声特征息息相关,该方法只能去除特征固定的噪声(Manoj and Nagarajan,2003).Kalman滤波的优点是可以去除不相关的脉冲噪声(Andrzej et al.,2009),实践过程中我们发现,过程噪声和测量噪声的协方差难以确定.EMD可以按频率高低自适应地分解复杂的非平稳信号,去除频率固定的噪声,如工频干扰,但对于频率成分复杂的噪声,阀值的设定往往难以把握,分解速度慢,实用性不强(蔡剑华,2010).形态滤波可以有效提取MT信号中的基线漂移和大尺度强干扰噪声,计算速度快,但依赖于结构元素形态和大小的选取(汤井田等,2012a).IARWR方法通过方差比识别噪声,利用维纳滤波去除突变噪声,提高低频数据质量,但对滤波后数据精确度缺乏有效验证,还会引入阶跃噪声(Kappler,2012).有学者把时域中的MT噪声处理比喻为给原始观测数据“动手术”,用以说明时域去噪的必要性和需要注意的问题.一则,对于强干扰噪声,如矿区的方波噪声和脉冲噪声,目前频域的去噪方法很难消除,只能在时域中进行预处理;二则,在时域去除噪声必须十分谨慎,确保有效信号不被滤除,否则即使得到了光滑的MT测深曲线,其正确性也无法保证.总而言之,对强干扰噪声,尤其是电场噪声,目前还缺少有效的抑制方法,从时域或时频域去噪将是MT噪声处理的主要发展方向.
随着我国“深部探测技术与实验研究(SinoProbe)”专项的启动,在全国范围内开展了阵列式大地电磁测深数据的观测(董树文等,2012;叶高峰等,2010),在对实测资料的处理中我们发现,山西和华南某些地区的数据受到严重的人文噪声干扰,干扰源主要有:高压线、铁路、公路、发电站、采矿区等;这些噪声最主要的特点是能级高、频带宽、噪声波形复杂多变(汤井田,2012b),采用传统处理方法得到的测深曲线具有明显的近场源效应,甚至全频段的数据都无法使用;如何在强干扰地区提高MT资料的信噪比是一项具有重要实际意义的工作.
本文从多道同步的MT时间序列出发,讨论了多道信号之间的依赖关系,通过对多站同步实测数据的分析验证了依赖关系的稳定性;同时,通过压制仿真噪声的试算,验证了基于多道时间序列依赖关系噪声处理的可行性和正确性;最后,处理了实测含噪声数据.结果表明,该方法可以有效去除脉冲、方波和充放电等强干扰噪声,抑制近场源噪声对MT测深曲线的影响,提高数据质量.
2 基本原理
可以把MT工作的基本原理看成一个线性系统(Jones et al.,1989),磁场为输入信号,通过地球这个特殊的系统,输出电场,通过测量电磁场就可以估算系统的传递函数,即阻抗,阻抗是稳定的,通常情况下与时间无关,这是我们利用MT方法探测地下介质电性结构的物理基础.因此,虽然电磁场信号的随机性很强(Luciano et al.,2011),但同一测点磁场与电场是互相依赖的,不同测点同步的磁场信号具有较强的相关性(图1),电场信号之间的差异主要是由测点间地下介质的电性结构差异引起的,但这种差异是稳定的,如同两个具有强相关的输入信号,分别通过稳定的系统后,得到的输出信号应具有某种相关性,因此不同测点的电场信号之间也应具有相对稳定的关系,总而言之,同步多道电磁场信号之间应具有相对稳定的依赖关系.当本地点电场或磁场信号在某些时刻受到噪声干扰时,利用这种依赖关系和参考点的数据,合成本地道受干扰时段的数据,用合成数据代替噪声段数据,组成新数据,就可以达到去除噪声的目的.
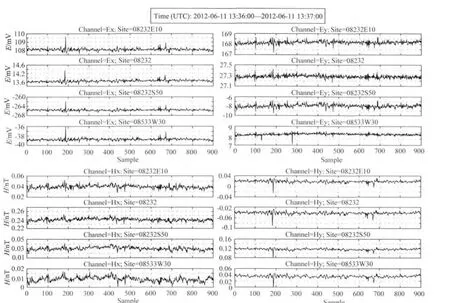
图1 同步大地电磁时间序列信号Fig.1 Time series of synchronous MT signals
实现这种方法需要解决两个基本问题,一是依赖关系的求取方法,二是依赖关系的稳定性.我们选取四个同步测点的高信噪比数据作为理想信号,用来讨论这两个基本问题,测点的点位分布如图2所示.测点位于西藏无人区,远离人文噪声干扰,其测深曲线如图3所示,曲线连续光滑,误差棒很小,忽略仪器噪声,可以将此数据作为理想信号.
2.1 依赖关系的求取
不失一般性,我们选取08232E10(参考点)的数据合成一段08232(本地点)的数据,具体计算方法如下,首先在本地道(如Ex)t0时刻,取出长度为T的数据段,记为d,M为此时参考点K道(RREx,RREy,RRHx,RRHy,K=4)数据组成的矩阵,假定d与M之间关系为φ,则有:

展开有:

将(2)式改写成矩阵表示为
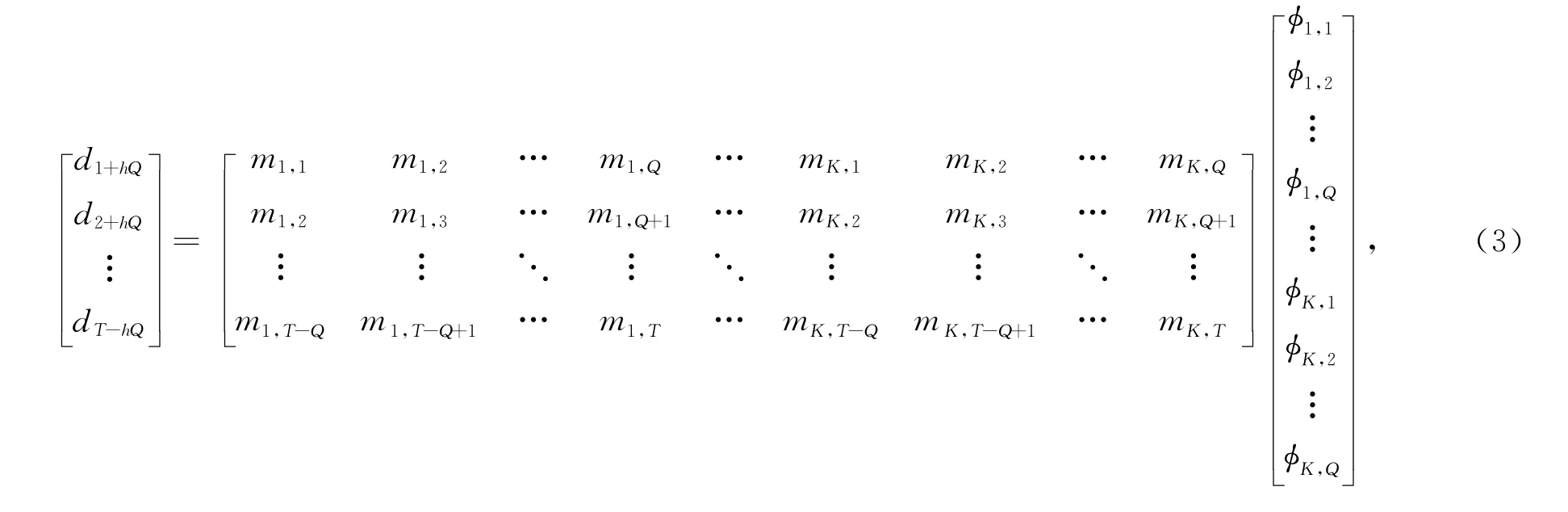
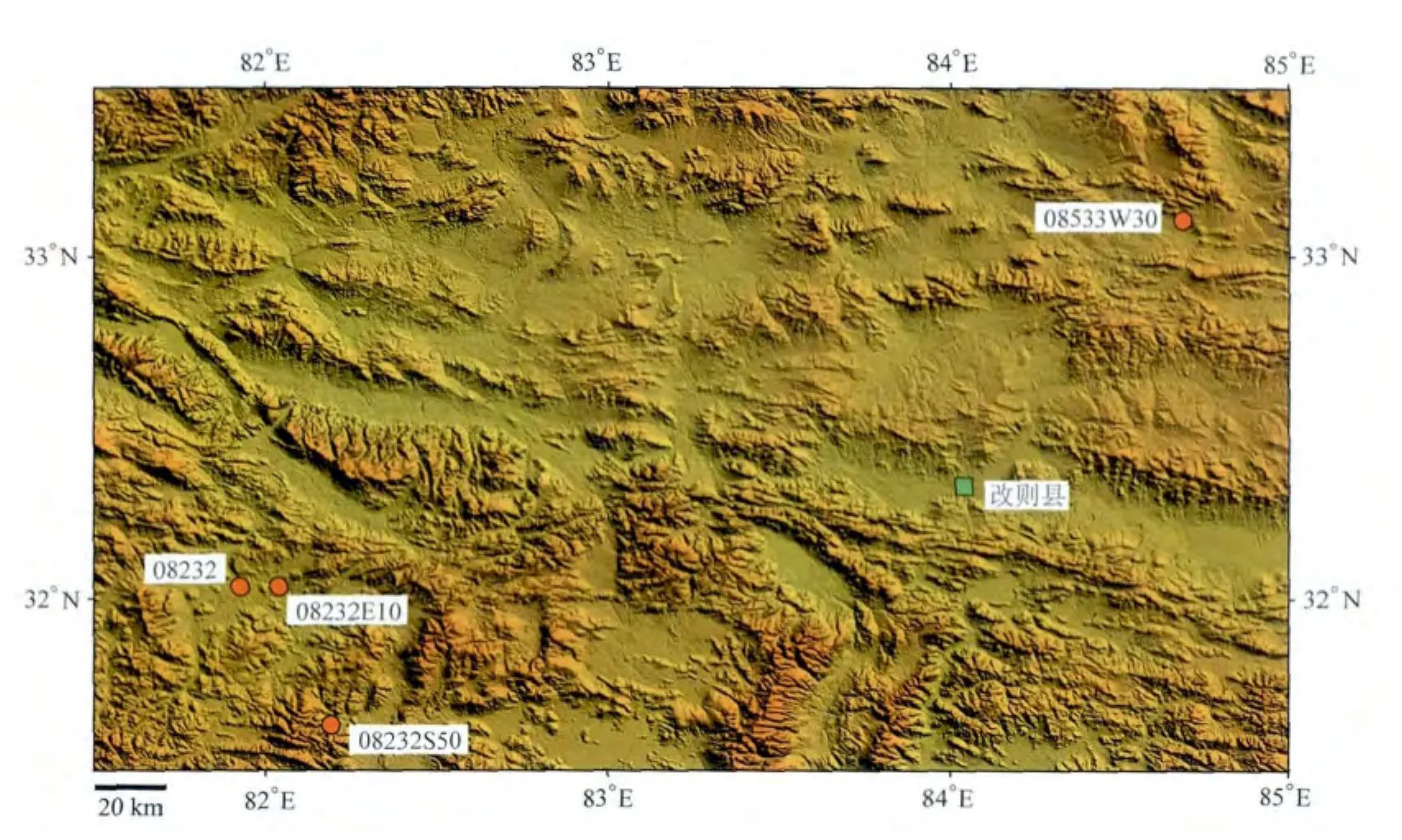
图2 MT测点点位分布图Fig.2 Topography map showing MT stations layout
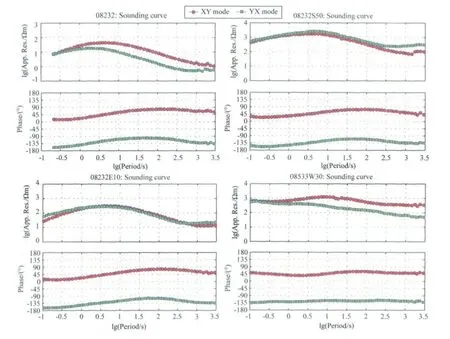
图3 高信噪比实测数据测深曲线Fig.3 MT sounding curves of practical data with high SNR
其中:mi,j表示第i个道的第j个数据,φi,j是mi,j对应的滤波系数.
由(3)式可以看出,d中的第n个值是由K个道的第(n-hQ)~(n+hQ)数据加权求和得到的,φ的本质是加权系数或滤波系数.
为了求解滤波系数矩阵φ,假定φ不随时间变化,因此可以选取另一时段t1,长度为Tp的数据重新组成M和d,求解t1时段的φ,注意此时M和d数据必须是高信噪比的,代表的是天然大地电磁场信号的特征,称为先验数据,这相当于利用理想的输入输出信号求解系统响应,基于最小均方误差准则,类似于最小二乘法估算阻抗,容易得到:
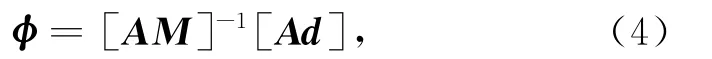
其中:
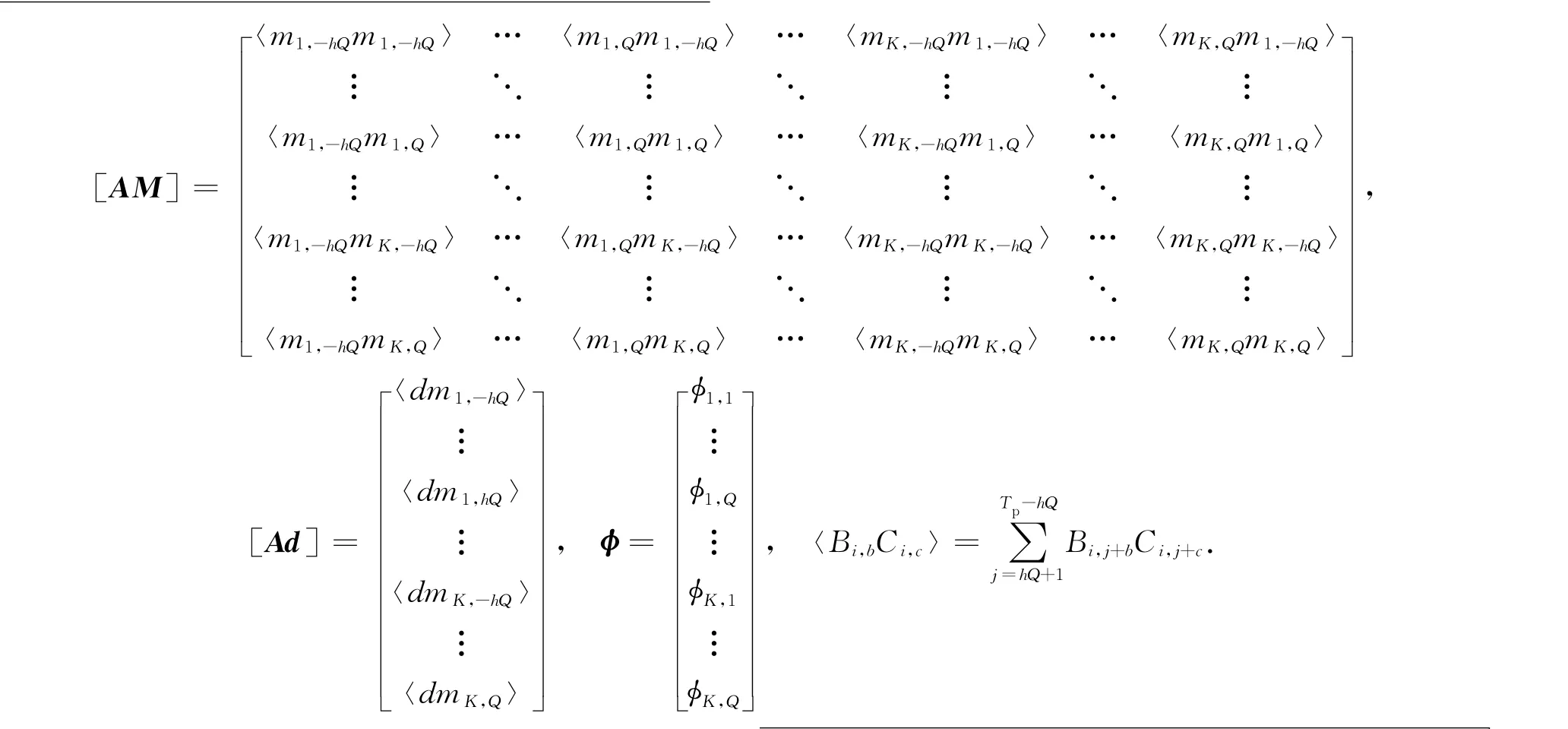
由于先验数据噪声水平低,因此用(4)式求得的滤波系数φ表示的是信号之间的依赖关系,再由(1)式就可以求得t0时段本地道(Ex)的合成数据,注意(1)式中的M是t0时段的.
2.2 依赖关系稳定性测试
从图3中不难看出,08232S50和08232E10测点的两个模式视电阻率曲线基本重合,说明两者一维性较强,但两者视电阻率值相差较大,08232和08533W30测点高频部分XY模式和YX模式电阻率曲线重合,两种模式电阻率曲线在中低频分开,说明浅部介质一维性较强,深部可能存在二维或三维的电性构造,但08232视电阻率值较小,08533W30视电阻率值较大.表1是四个测点视电阻率值和相位值的统计结果,从表中也不难发现四个测点视电阻率值具有明显差异,因此,四个测点地下介质的电性构造存在明显差异,从图1中也可以看出,四者的电场信号存在一定差异,但磁场信号仍具有很强的相关性.
测试方法如下:选择与本地点具有不同参考距离,且存在明显电性结构差异的三个参考点,再从中选取不同时段、不同长度的先验数据求取信号间的依赖关系,最后合成本地点(08232)的同一段数据.用合成数据与原始理想数据的相干度,衡量合成数据的精确度,以此验证φ的稳定性.如图4所示,从08232选取一道长度为30的原始数据(如Ey),记为dori,在dori的后方分别选取30段长度不同的先验数据dpriori,先验数据的长度按对数等分,原始数据和先验数据的时段分别为t0、tp,另外对不同参考点而言,选取的先验数据时段是不同的,如图中tps,最后合成t0时段的Ey道数据记为dsyn,合成数据和原始数据相干度与先验数据长度的关系如图5所示.
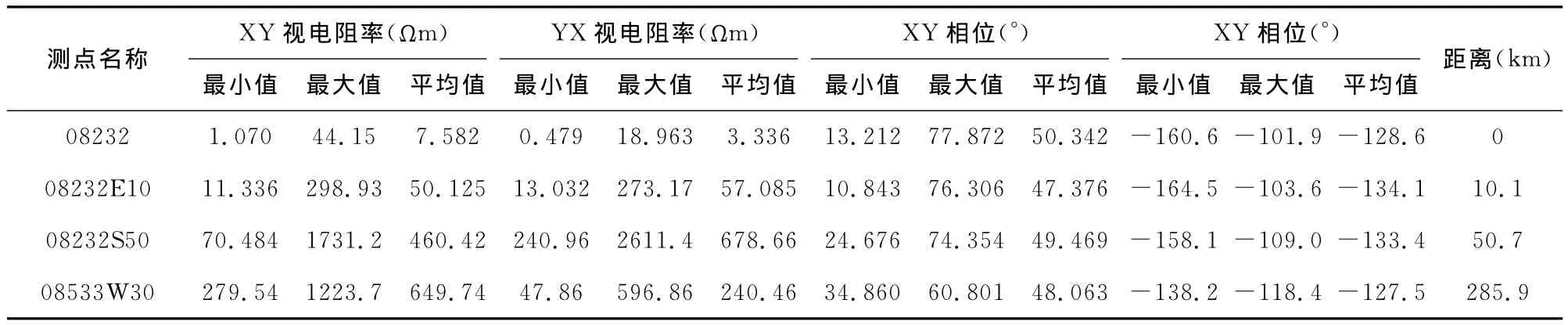
表1 图2中测点视电阻率值和相位值的统计Table 1 Statistics of apparent resistivity and phase values calculated from the sounding sites in Fig.2

图4 先验数据的选取示意图Fig.4 Selecting scheme of priori data

图5 参考点和先验数据长度对合成数据精度的影响Fig.5 Influence on accuracy of synthetic data by altering reference sites and length of priori data
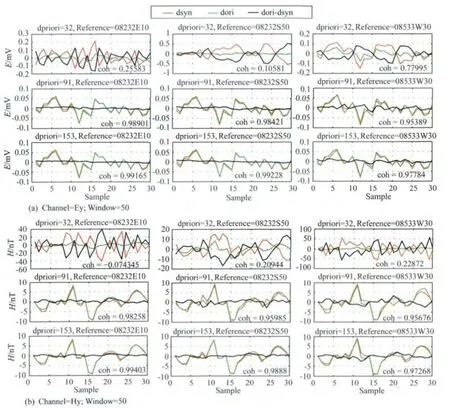
图6 不同参考点和先验数据长度的合成数据Fig.6 Synthetic data of different reference sites and lengths of priori data
由图5可知:①利用不同参考点求得的依赖关系即使是不同的,却都可以精确地合成同一段本地点的数据;②无论磁场或电场信号,都可以通过参考点数据合成,且精度都较高;③在对数坐标下,当先验数据长度与合成数据长度的比值小于0.5时,合成数据与原始数据的相干度小于0.8,且不稳定,当两者比值大于0.5(先验数据长度约为合成数据长度的3倍)时,合成数据与原始数据的相干度接近于1,两者基本一致.图6是不同先验数据长度下,合成数据与原始数据的对比图.
由图6可知,当先验数据长度为91和153时,合成数据与原始数据基本一致,两者的相干度在0.95以上,当先验数据长度为32时,两者相干度小于0.8,说明选择较长时段信号求得的依赖关系包含了短时段信号之间的关系,从大地电磁信号特征的角度也不难理解,即短时段信号的频谱信息包含在长时段信号当中.
上述试算结果表明,选择不同参考距离、不同电性结构参考点的不同时段的先验数据,都可以精确地合成同一段本地点的数据,说明多道同步大地电磁信号之间的依赖关系是稳定的,其一,对同一参考点而言,依赖关系与先验数据的时段无关,只与先验数据的长度有关;其二,即使不同参考点信号存在差异,依赖关系不同,但只要选择足够长高信噪比的先验数据,就可以精确合成同一段本地点的数据.因此,选择较长的、低噪声的先验数据(大于3倍噪声段数据长度)尤为重要,在实际应用过程中,需要人为挑选先验数据.
3 仿真试算
天然大地电磁信号微弱,频带宽,与复杂的人文噪声耦合在一起,难以区分.时域中处理噪声的难点在于,去除强干扰噪声的同时要保留微弱的有效信号成分,过分追求连续光滑的测深曲线,而忽略微弱的信号,可能会导致对地下介质电性结构的错误认识.为了试验本文方法的有效性和正确性,进行如下仿真试算.
(1)仿真噪声
对08232(本地点)测点四个水平分量加入仿真噪声,以08232E10测点作为参考点,两点相距10.1km.仿真噪声由方波、三角波和脉冲这三种常见的强干扰噪声(汤井田,2012a)随机组合而成,其形态和幅值也是随机的,对每个信号道,随机选择20%的窗口加入噪声;加入噪声后的数据如图8中dnoise所示.
(2)噪声识别
利用本地道与参考道时间序列的方差比识别噪声(Kappler,2012).首先对同步后的数据加窗,用wk,n表示 第k道 第n个 窗 口 的 数 据,var(wk,n)和rrvar(wk,n)分别表示为本地道数据和参考道数据的方差,当var(wk,n)/rrvar(wk,n)>th时,th为阀值,则认为本地点第k道第n个窗口的数据含有噪声.这种方法基于强噪声具有突变性从而引起方差变化的特点,从时域中定位本地点噪声所在的通道和时段.图7是对仿真噪声的识别结果,识别率达到99.8%.
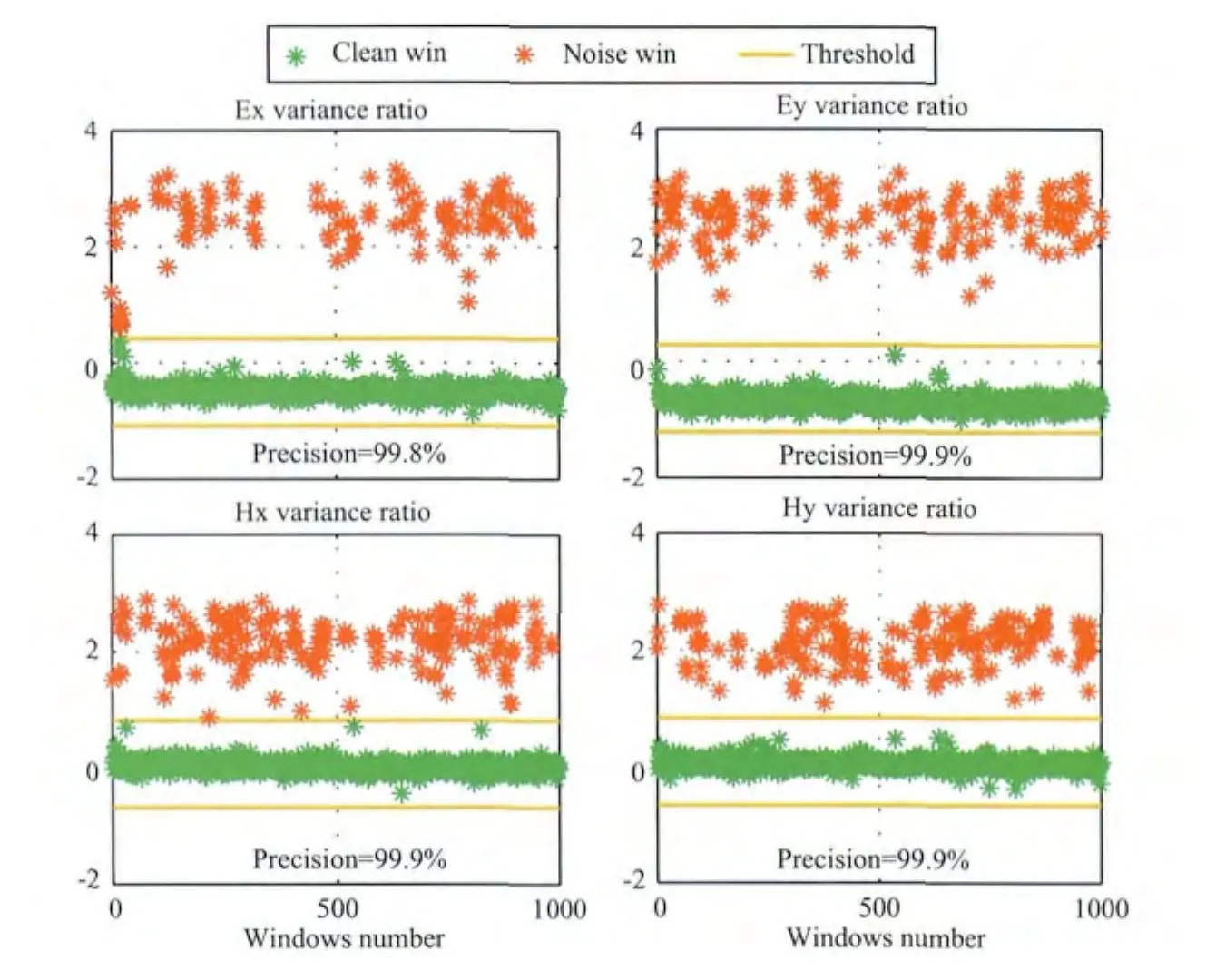
图7 方差比对仿真噪声的识别Fig.7 Identification of simulation noise by variance ratio method
(3)合成数据
选择一段未加入噪声的本地点数据和参考点数据作为先验数据,为了保证先验数据长度大于噪声段数据长度的3倍,先验数据长度为2min(time=2012-06-1114∶06∶02—14∶08∶02),共1800个采样点,窗口长度为30个采样点,按2.1节所述,用本文方法对识别后的噪声进行时域处理,用合成数据替换噪声数据得到新数据.图8是原始数据、噪声数据和合成数据的对比图.
从图8中可以看出合成数据成功去除了仿真噪声,与原始信号数据一致,两者的相干度高达0.99.
(4)测深曲线对比
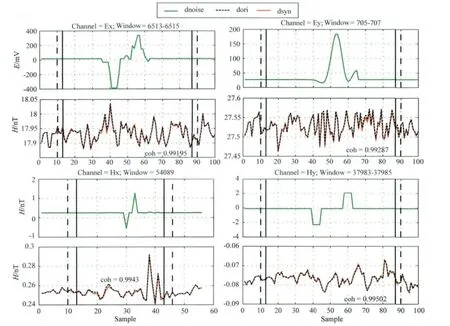
图8 原始数据、人工噪声数据和合成数据的对比Fig.8 Comparison of original signals,artificial noisy data and synthetic data
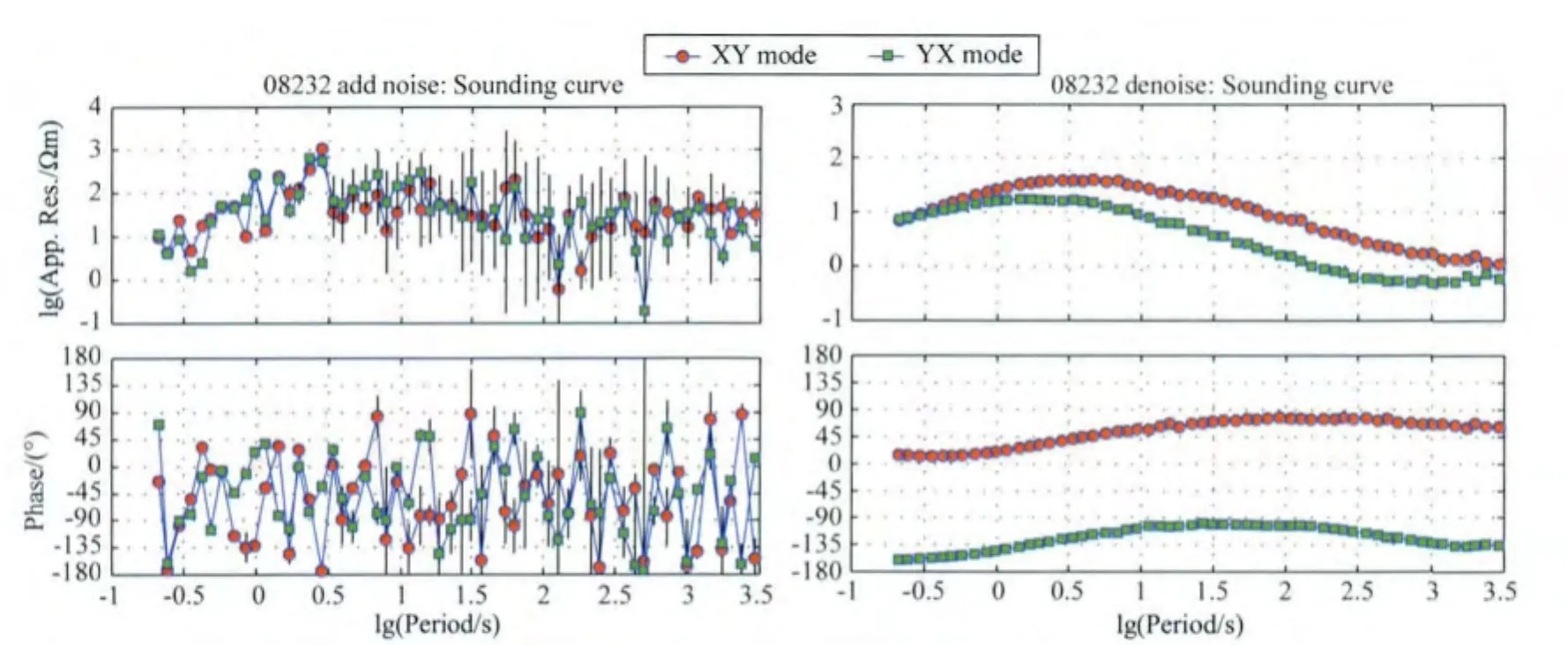
图9 人工噪声数据和新数据测深曲线的对比Fig.9 Comparison of MT sounding curves between artificial noisy data and new data
仿真噪声数据和去噪后数据的测深曲线如图9所示,可以看出,加入噪声后,视电阻率和相位曲线出现了很多“飞点”,难以分辨曲线形态,无法用于后续反演计算,新数据的测深曲线与原始曲线(图3中08232)一致.仿真噪声试验结果表明,用方差比方法可以精确识别方波、脉冲和三角波等典型的干扰噪声,利用本文方法得到的合成数据去除了噪声,保留了微弱的有效信号,提高了大地电磁测深资料的数据质量和可信度.
4 参考点噪声测试
为了研究参考点数据噪声水平对合成数据精度的影响,进行如下试算,对08232E10号测点(参考点)四道所有时段的数据,加入不同信噪比的高斯噪声,再对上述仿真噪声数据进行处理,处理步骤与第3节相同.选择图8中的Ey数据,考察合成数据精度与参考点信噪比之间的关系,如图10所示,随着参考点数据信噪比的提高,合成数据与原始数据的相干度也随之增大,当信噪比大于等于40dB时,两者的相干度大于0.94,当信噪比小于30dB时,相干度急剧下降,说明当参考点噪声较强时,合成数据的误差较大,这是因为参考点噪声较强时,求得的本地点与参考点数据之间的关系并不完全表征信号间的依赖关系,而且用于计算合成数据的参考点数据含有噪声,也会增大合成数据的误差.
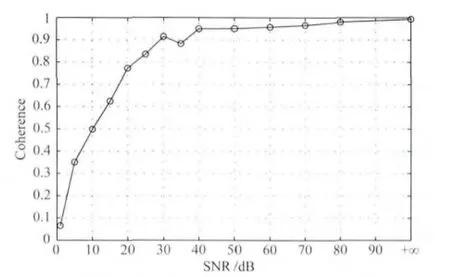
图10 合成数据精度与参考点数据信噪比的关系Fig.10 Relationship between the accuracy of synthetic data and SNR of reference data
图11 是参考点加入信噪比分别为10dB、20 dB、40dB和80dB的噪声后,合成数据与原始数据的对比图.从图中容易看出,当参考点信噪比增大时,合成数据越接近于原始数据,当信噪比较低时,合成数据与原始数据的变化趋势基本一致,幅值相差较大,合成数据的精度较低,但与仿真噪声数据(图8)相比,合成数据的误差比噪声要小得多.
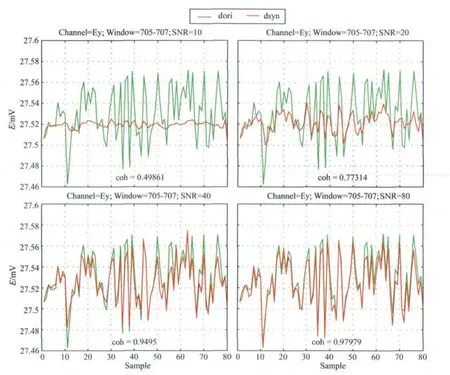
图11 参考点信噪比不同时的合成数据Fig.11 Variation of synthetic data with reference data for different SNR

图12 参考点信噪比不同时08232测点的测深曲线Fig.12 MT sounding curves of site 08232with reference data for different SNR

图13 3005(本地点)和1605(参考点)测点的先验数据Fig.13 Priori data of 3005(local)and 1605(reference)sites
图12 是参考点信噪比分别为20dB和40dB时,用本文方法处理仿真噪声数据后得到的测深曲线图.与图9对比易知,即使参考点数据含有噪声,也可以得到正确且较光滑的测深曲线,当参考点数据信噪比增大时,测深曲线越接近于原始测深曲线.在基本理论部分,已经论证了合成数据的精度与参考点的距离及电性结构无关,因此实际应用中,首先要考虑将参考点布设在没有人文噪声干扰的“安静”环境中,从而保证合成数据的精度.
5 实测数据试算
3005(本地点)和1605(参考点)大地电磁测点位于江西赣州,两点相距112km,1605号点位于稻田中,周围1km内无明显干扰源,数据质量较高,3005号测点距一个大型火力发电站约2km,周围有很多高压线.从其测深曲线(图15a)上可以发现,中高频段数据受到明显的近场源噪声干扰,视电阻率曲线呈约45°直线上升,相位接近于0°或180°.从时间序列信号中,我们发现很多类似方波、脉冲、三角波等突变噪声,噪声强度大,分布广,部分时间序列如图14中dori所示.经本文方法处理后得到的合成数据如图14中dsyn,新数据测深曲线如图15b所示.本例中选择的先验数据如图13所示,长度为2min,共1800个采样点,窗口长度为30个采样点,先验数据不含明显噪声,其中Hx和Hy相关性较好,Ex和Ey相差较大,但这并不影响去噪的结果.
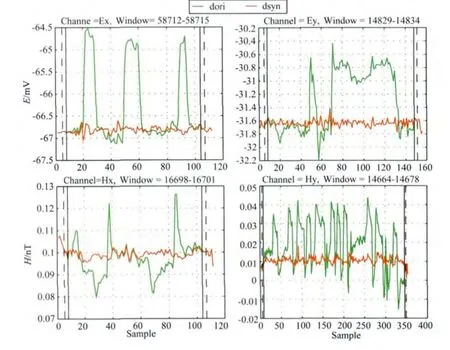
图14 3005测点原始数据与合成数据的对比Fig.14 Comparison of original data and synthetic signal of site 3005
从图14中容易看出,合成数据去除了原始数据中的强干扰噪声,保留了微弱变化的有效信号.从图15中不难看出,新数据有效抑制了中高频段的近场源效应,提高了视电阻率和相位曲线数据质量,只是在1Hz附近几个频点上还存在“跳点”.
6 存在的问题及改进方法
当时间序列中含有阶跃噪声时,单用方差比方法是无法识别的,如图16中椭圆标出区域所示,方差代表的是数据的波动情况,整体抬升或下降的噪声数据,其方差是不变的,因此单用方差比无法识别阶跃噪声,所以新数据中仍保留了阶跃噪声,如图16中dnew所示.
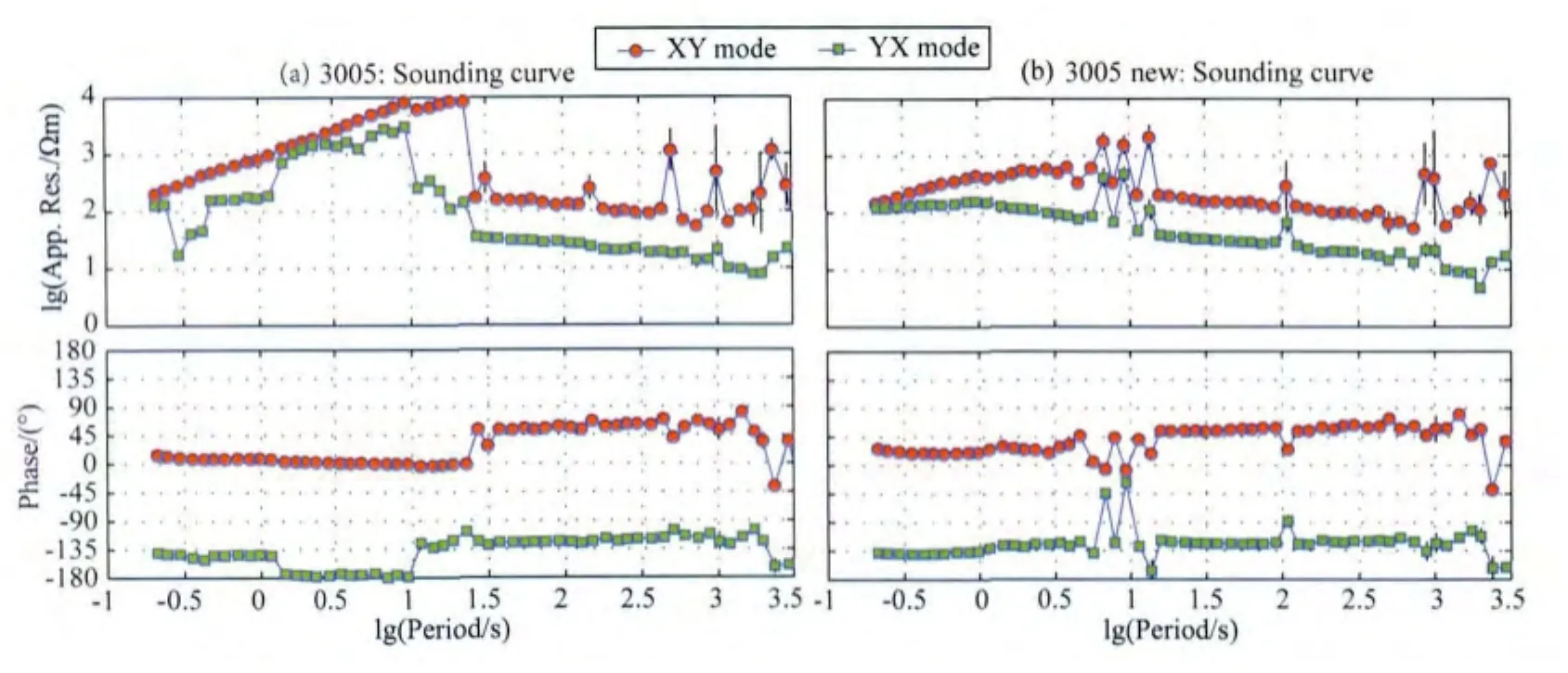
图15 3005号点测深曲线(a)原始数据测深曲线;(b)新数据测深曲线.Fig.15 MT sounding curves of site 3005(a)Original data;(b)New data.
(1)平移法去除方波噪声
方波噪声可以看成一种特殊的阶跃噪声,识别方波噪声最直接的方法是延长窗口长度,如图16a所示,当窗口长度大于c2时,仍用方差比方法就能识别c2段的噪声数据.但是在试算的过程中我们发现,为了保证合成数据的精度,延长窗口长度的同时必须增大先验数据的长度,而在强干扰地区,很难找到持续时间较长的高信噪比数据作为先验数据,因为窗口长度太长,先验数据含有明显噪声或长度不够,将导致合成数据的精度大大降低,甚至引入“假信号”,正如图6中先验数据长度为32时的情况,因此延长窗口长度的方法不适用于强干扰地区去除方波噪声.
根据阶跃噪声具有突变性和突变前后信号变化不大的特点,如图16a中c1至c2有突变,但两者本身变化不大,因此可以用(5)式进行识别.
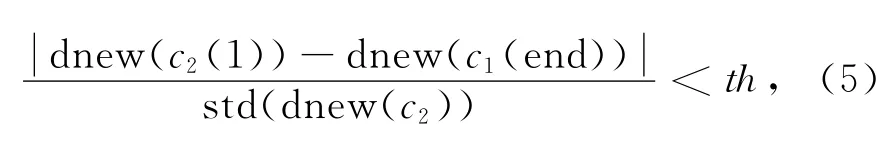
std为求标准差,th为阀值,c2(1)为c2段第一个数据,c1(end)为c1段最后一个数据,为了避免将信号误判为噪声,th的值不易太小,试算发现电场阀值th=5~10,磁场阀值th=10~20时,可以识别幅值较大的阶跃噪声.定位噪声后,对c2段数据按(6)式平移,就可以去除方波噪声,记为ddesquare.
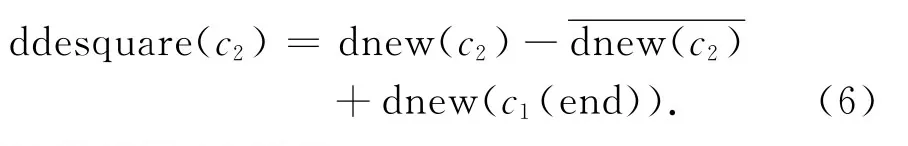
试算结果如图16所示.
图16表明,结合(5)式和(6)式可以有效识别和去除幅值较大的方波噪声,保留了微弱的有效信号.图17是3005号测点去除方波噪声后,单点处理和远参考处理得到的测深曲线图,对比图17a与图15b可知,去除方波噪声后的测深曲线基本消除了中高频近场源效应的影响和个别频点“跳点”的情况,再经远参考处理后,测深曲线更加光滑.因此,通过本文时域噪声处理方法和频域远参考技术的综合处理,可以有效抑制近场源干扰,提高强干扰地区MT资料的信噪比.
(2)人为噪声
平移法只能去除较理想的方波噪声,真实噪声是复杂的,平移后的数据看似消除了方波噪声,实则引入了人为噪声,但人为噪声相对于原始方波噪声是较小的,通过Robust估计和远参考处理可以抑制人为噪声的影响,如图17所示.为了确保去噪后数据的正确性,阀值的选择不易太大,以免去除有效信号,另外,(5)式也可以识别阶跃噪声,但(6)式不能去除阶跃噪声,其难点在于信号“基准线”难以确定.
7 结论
本文从理论上探讨了多道同步大地电磁时间序列信号之间的依赖关系φ,选择一段低噪声的数据作为先验数据,用最小二乘法估算φ,再结合参考道的数据,合成本地道含噪声时段的数据,用合成数据代替噪声数据得到新数据,就可以在时域处理大地电磁噪声.该方法避免了传统方法中信噪分离的思路,直接利用参考道的信号合成本地道信号,无需考虑复杂的人文噪声,且合成数据的精度较高.
对西藏无人区高信噪比实测数据的试算结果表明,φ是相对稳定的,对同一参考点而言,与选择的先验数据时段无关,只与先验数据的长度有关;对不同参考点而言,即使φ不相同,但结合各参考点的数据,都可以精确合成本地点的同一段信号,与参考点地下电性结构和参考距离无关.
仿真噪声的试算结果表明,方差比方法可以有效定位方波、脉冲和三角波等强干扰噪声,合成数据与原始数据一致,对应的测深曲线也一致;对参考点数据加入随机噪声的试算结果表明,合成数据的精度会随着参考点数据信噪比的减小而降低,但与强噪声相比,合成数据的影响要小得多.实测数据的处理结果表明,该方法可以有效抑制近场源强干扰噪声,保留微弱的有效信号,提高测深曲线光滑性和连续性的同时保证了其正确性.针对方差比无法识别持续时间较长的方波噪声的问题,提出了一种简单的改进方法,对实测数据的处理结果表明,该方法可以有效识别和去除方波噪声.将本文方法与远参考技术相结合,可以有效抑制MT资料的近场源效应,提高强干扰地区MT资料的利用率.
实际应用本文方法时,要尽可能选择没有人文噪声干扰的环境布设参考点,提高参考点的信噪比;先验数据的选择非常关键,需要人为手动挑选没有明显噪声干扰时段的数据,保证先验数据求得的φ,表征的是天然场信号间的依赖关系,先验数据的长度至少要大于噪声段数据长度的3倍.
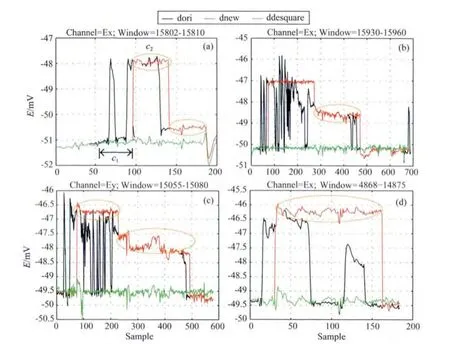
图16 方波噪声的识别及去除Fig.16 Identification and removal of square wave noise
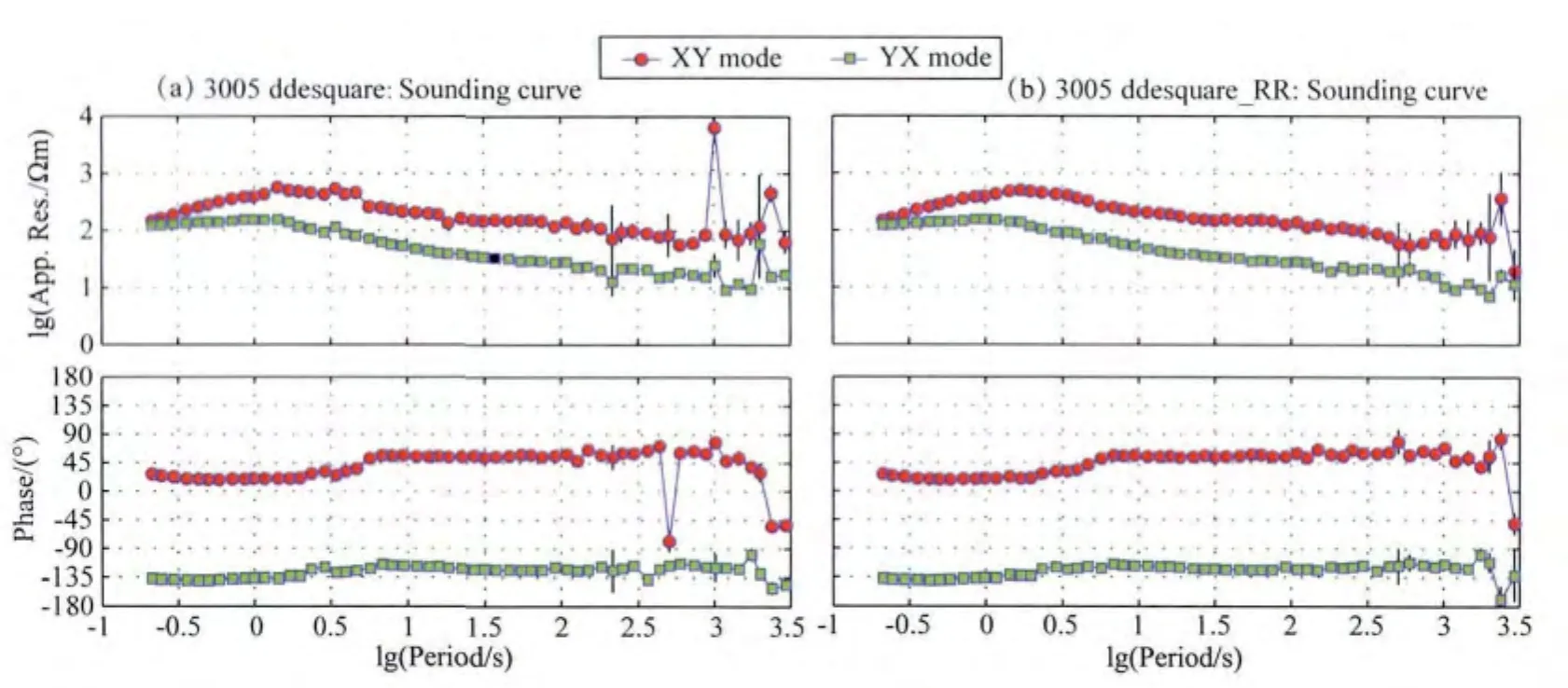
图17 3005测点测深曲线(a)去除方波噪声+单点处理;(b)去除方波噪声+远参考处理.Fig.17 MT sounding curves of site 3005(a)Square wave removed with standard procedure;(b)Square wave removed with remote reference technique.
虽然强干扰地区噪声强度大、成分复杂,但只要能够找到一段没有明显噪声的数据,就可以利用该方法去噪,而且处理过程中没有改变时间序列数据格式,后续数据处理采用成熟的商业软件即可完成,实用性较强.
致谢 非常感谢魏文博教授在研究过程中细心的教导和帮助,以及对文章初稿的审阅和给出的宝贵意见,还要感谢张乐天师兄提供最新的文献资料和董浩师兄在编写代码时给予的帮助.
Andrzej L,Danek T,Wojdyla M.2009.Application of kalman filter to noise reduction in multichannel data.SchedaeInformaticae,17(1):63-73.
Bai D H,Unsworth M J,Meju M A,et al.2010.Crustal deformation of the eastern Tibetan plateau revealed by magnetotelluric imaging.NatureGeoscience,3(5):358-362.
Cagniard L.1953.Basic theory of the magnetotelluric method of geophysical prospecting.Geophysics,18(3):605-635.
Cai J H.2010.Study on processing of method of magnetotelluric signal and its application based on Hilbert-Huang transform[Ph.D.thesis](in Chinese).Changsha:Central South University.Chen J,Heincke B,Jegen M,et al.2012.Using empirical mode decomposition to process marine magnetotelluric data.Geophysical JournalInternational,190(1):293-309.
Daniel O T,Travassos J M.2000.Wavelet filtering of magnetotelluric data.Geophysics,65(2):482-491.
Dong S W,Li T D,Chen X H,et al.2012.Progress of deep exploration in mainland China:A review.ChineseJournalof Geophysics(in Chinese),55(12):3884-3901.
Egbert G D,Booker J R.1986.Robust estimation of geomagnetic transfer functions.GeophysicalJournalInternational,87(1):173-194.
Egbert G D.1997.Robust multiple-station magnetotelluric data processing.GeophysicalJournalInternational,130(2):475-496.
Gamble T D,Goubau W M,Clarke J.1979a.Magnetotellurics with a remote magnetic reference.Geophysics,44(1):53-68.
Gamble T D,Goubau W M,Clarke J.1979b.Error analysis for remote reference magnetotellurics.Geophysics,44(5):959-968.
Jin S,Zhang L T,Jin Y J,et al.2012.Crustal electrical structure along the Hezuo-Dajing profile across the northeastern margin of the Tibetan Plateau.ChineseJournalofGeophysics(in Chinese),55(12):3979-3990.
Jing J E,Wei W B,Chen H Y,et al.2012.Magnetotelluric sounding data processing based on generalized S transformation.ChineseJournalofGeophysics(in Chinese),55(12):4015-4022.
Jones A G,Chave A D,Egbert G,et al.1989.A comparison of techniques for magnetotelluric response function estimation.JournalofGeophysicalResearch,94(10):201-213.
Junge A.1996.Characterization of and correction for cultural noise.SurveysinGeophysics,17(4):361-391.
Kappler K N.2012.A data variance technique for automated despiking of magnetotelluric data with a remote reference.GeophysicalProspecting,60(1):179-191.
Luciano T,Lovallo M,Han-Lun H,et al.2011.Analysis of dynamics in magnetotelluric data by using the Fisher-Shannon method.PhysicaA:StatisticalMechanicsandItsApplications,390(7):1350-1355.
Manoj C,Nagarajan N.2003.The application of artificial neural networks to magnetotelluric time-series analysis.Geophysical JournalInternational,153(2):409-423.
Shalivahan,Bhattacharya B B.2002.How remote can the far remote reference site for magnetotelluric measurements be?JournalofGeophysicalResearch,107(6):119-126.
Tang J T,Li J,Xiao X,et al.2012a.Mathematical morphology filtering and noise suppression of magnetotelluric sounding data.ChineseJournalofGeophysics(in Chinese),55(5):1784-1793.
Tang J T,Xu Z M,Xiao X,et al.2012b.Effect rules of strong noise on magnetotelluric sounding in the Luzong ore cluster area.ChineseJournalofGeophysics(in Chinese),55(12):4147-4159.
Wang S M,Wang G Y.2004.Statistical analysis of magnetotelluric signal.ActaSeismologicaSinica(in Chinese),26(6):669-674.
Wei W B.2002.Progress and prospects of magnetotelluric sounding in China.ProgressinGeophysics(in Chinese),17(2):245-254.
Wei W B,Unsworth M,Jones A G,et al.2001.Detection of widespread fluids in the Tibetan crust by magnetotelluric studies.Science,292(5517):716-719.
Xie C L,Ye G F,Wei W B,et al.2012.Electrical features of the main faults beneath northern Tibetan Plateau.ChineseJournal ofGeophysics(in Chinese),55(12):3991-4002.
Xu Y X,Wang G Y.2000.Power spectrum estimation for magnetotelluric signal based on continuous wavelet transform.ChineseJournalofGeophysics(in Chinese),43(5):677-683.Ye G F,Wei W B,Deng M,et al.2010.Construction methods and experiments for magnetotelluric standard network at the Tibetan Plateau and North China.ActaGeologicaSinica(in Chinese),84(6):801-807.
Zhang L T,Jin S,Wei W B,et al.2012.Electrical structure of crust and upper mantle beneath the eastern margin of Tibetan plateau and the Sichuan basin.ChineseJournalofGeophysics(in Chinese),55(12):4126-4137.
附中文参考文献
蔡剑华.2010.基于Hilbert-Huang变换的大地电磁信号处理方法与应用研究[博士论文].长沙:中南大学.
董树文,李廷栋,陈宣华等.2012.我国深部探测技术与实验研究进展综述.地球物理学报,55(12):3884-3901.
金胜,张乐天,金永吉等.2012.青藏高原东北缘合作—大井剖面地壳电性结构研究.地球物理学报,55(12):3979-3990.
景建恩,魏文博,陈海燕等.2012.基于广义S变换的大地电磁测深数据处理.地球物理学报,55(12):4015-4022.
汤井田,李晋,肖晓等.2012a.数学形态滤波与大地电磁噪声压制.地球物理学报,55(5):1784-1793.
汤井田,徐志敏,肖晓等.2012b.庐枞矿集区大地电磁测深强噪声的影响规律.地球物理学报,55(12):4147-4159.
王书明,王家映.2004.大地电磁信号统计特征分析.地震学报,26(6):669-674.
魏文博.2002.我国大地电磁测深新进展及瞻望.地球物理学进展,17(2):245-254.
谢成良,叶高峰,魏文博等.2012.藏北高原主要断裂带电性结构特征.地球物理学报,55(12):3991-4002.
徐义贤,王家映.2000.基于连续小波变换的大地电磁信号谱估计方法.地球物理学报,43(5):677-683.
叶高峰,魏文博,邓明等.2010.青藏及华北阵列式区域大地电磁场标准观测网建设方法与实验.地质学报,84(6):801-807.
张乐天,金胜,魏文博等.2012.青藏高原东缘及四川盆地的壳幔导电性结构研究.地球物理学报,55(12):4126-4137.

