弹性回跳模型:从经典走向未来

刘力强

(中国地震局地质研究所，地震动力学国家重点实验室 100029)

美国旧金山1906年大地震之后4年，数学物理博士、冰川学家Harry Fielding Reid发表了文章《地震力学》(The Mechanics of the Earthquake)(Reid，1910)。他利用旧金山地震后的现场调查资料与USGS的地震数据，清晰明确地阐述了断层与浅源地震之间的相关性，首次提出用弹性回跳模型来解释浅源地震的力学机制。弹性回跳理论使Reid作为地震学家声名鹊起，文章发表的第2年Reid被约翰·霍普金斯大学晋升为地质与地貌动力学教授，同年被选为美国科学院院士，1924—1926年担任了美国地球物理学会(AGU)主席，后人称之为美国地球物理第一人。

弹性回跳模型包含3个基本要点:1)地震来自于断层的运动;2)断层运动导致其两侧的岩石弹性变形，积累巨大的能量，这个能量在地震中得以释放;3)在断层带的各个点上积累能量的过程是缓慢而不均匀的。

然而，弹性回跳面临一个难以回答的问题:震前的变形量到底有多大?Reid所绘制的震前栏杆式变形位错现象(图1)能被看到吗?USGS在介绍弹性回跳理论网页的最后，特别附加了一句:“这张图极大地夸张了变形量。实际上，变形分布在很宽阔的范围上，只有用精确的仪器才可能看到，例如GPS。”。这一句表面上是提醒读者的话，实际上把问题指向了Reid:1910年还没有GPS这样的高精度仪器，您是怎么看到震前变形的?Reid得到这个模型所依据的还真的不是栏杆式的变形，他只是画了一个示意图来解释弹性回跳模型，后人找到了Bolinas的照片放这里，恰好配成了一对。他所依据的是地震前后的大地三角测量。通过三角测量数据，他观测到了震前变形，并且注意到，变形强度随着远离断层带逐步变小。然而，没有全面给出变形量依旧是一个遗留问题。

弹性回跳理论留下的这个问题成了Reid的软肋，他在77岁高龄时遇到了来自 Jeffreys(1936)的挑战，其后的质疑声持续了近30年(Griggs et al.，1960;Orowan，1960)。他们主要的问题就是，震前滑动大变形必然带来断层的破裂，对于深部地震来说，高压高温环境下不能容许这样的滑动大变形。断层滑动不是必要的，岩石变形破裂就可以直接形成地震，这个方面的典型代表是基于扩容效应的所谓干湿模式(IPE与DD模式)。扩容模型解释了许多与地震相伴随的前兆现象，同时回避了震前沿断层带看不到滑动大变形的问题，作为震源模型曾经几乎替代了弹性回跳理论。但是扩容模型也遇到了无法解释的问题，例如地震分布确实与断层相关，地震应力降远远小于岩石破裂应力降等等。

Brace(1966)重新复活了Reid的模型，提出弹性回跳的物理机制应当用摩擦滑动过程中出现的不平稳滑动(jerky sliding motion)来解释，因为工程界有一个常用词汇——粘滑(stick-slip)所描述的现象与此类似，他借用来代替不平稳滑动。这篇文章对粘滑的概念阐述如下:“在室内地质材料实验中，摩擦滑动常常伴随有粘滑。地球上的浅源地震可以表述为新老断层滑动过程中的粘滑。在这种情形下，观测到的应力降代表了来自震源周围岩石中应力的一小部分释放。”有趣的是Brace的粘滑概念是指摩擦滑动过程中的一个伴随现象或者事件，他没有像一些后来者把粘与滑分开解释为滑动过程的2个阶段(Scholz，1998)，他还特别强调产生地震应力降的能量来自震源区的围岩。

粘滑概念的引入，统一了浅源地震与深源地震的物理解释，将变形问题转化为摩擦问题的研究，由此引发了20世纪70—90年代的摩擦研究热潮。12年后，Byerlee发表了其研究论文——岩石的摩擦(Friction of rock)(Byerlee，1978)。这篇论文影响很大，以至于被后人尊为拜尔利定律(Byerlee's Law)，他本人对这个定律的表述是:当正应力＜2kb时，引起断层滑动的剪应力近似为τ=0.85σn;正应力＞2kb时，剪应力近似为τ=0.5+0.65σn。给出这个结论之前，Byerlee有一段特别陈述:“实验结果表明，如同在大多数民用工程所遇到的，在低应力下岩石摩擦能够在非常大的范围与变差(variation)之间变化，这是由于低应力摩擦强烈地依赖于表面粗糙度。中等压力条件下，如采矿工程，高压条件下，如深部地壳断层滑动，原始表面粗糙度对摩擦就只有很小的、甚至没有影响。”从这一段陈述中，逻辑上读者应当期待一个低压情况下数据散点分布较宽，随着压力加大逐步收窄，以0.85为渐近线收敛的形态。有些令人不解的是，从Byerlee所给出的图中读者看不到这个趋势，甚至反而有可能是相反的情况(图2)。另外一个遗憾是，尽管Byerlee论文中多次提到数据的变差，但是对于这个重要的经验方程他自己却没有给出变差的范围，读者也就无从计算或者评价其可信度。进一步地，以分段函数表达的摩擦本构关系分界点取为2kb，这有何物理意义或者统计依据，也没有见到任何解释。

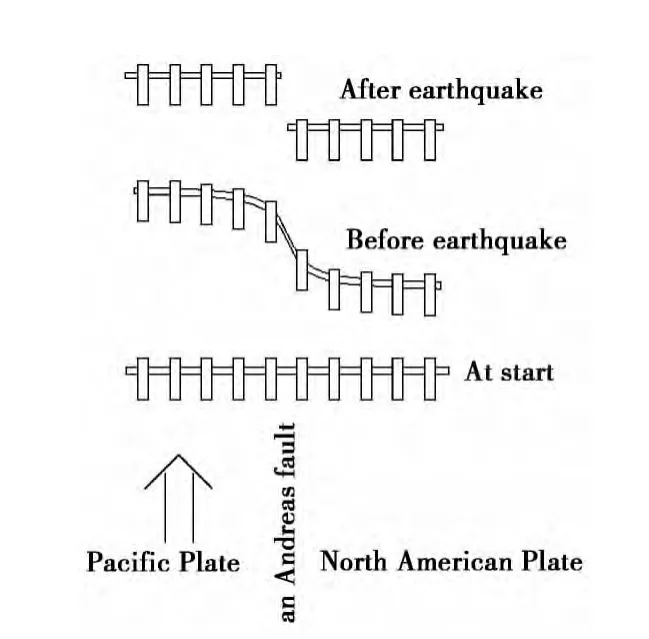
图1 弹性回跳示意图Fig.1 Sketch of elastic rebound model.引自 http://earthquake.usgs.gov/regional/nca/1906/18april/reid.php

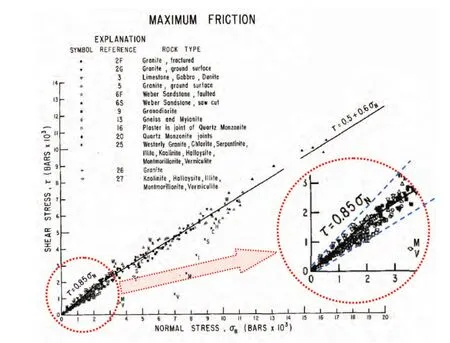
图2 Byerlee显示摩擦定律的数据散点图Fig.2 Scatter plot of data from Byerlee's Law.

摩擦概念的引入把沿着断层带的变形转换为了滑动，但是地震需要弹性能的释放，弹性变形依旧是必要的。在Byerlee摩擦理论框架里面，用弹簧滑块模型比拟粘滑，断层位移被设定为刚性块体的摩擦运动，变形被设定为弹簧的伸缩。Byerlee简单化地认定弹簧变形等同于实验加载机的机械框架的变形。这不但明显违背了Reid的原意与Brace的阐述，至少还没有论证各种加载设备之间的差异。Byerlee却仅仅用一段文字把它轻轻带过了:“幸运的是所有类型的仪器都给出了类似的结果，尽管在每一个仪器中构成弹簧的并不总是明确的。”于是，明确的沿断层带的变形被不明确的“远程”弹簧取代了。实验样品滑动面两侧围岩的变形被忽略，滑动面上的应力直接用载荷的投影来代替。

影响参数很多、离散很大的摩擦本构关系能够用一个常数来描述，断层面两侧复杂的变形可以不去考虑，直接用所施加的载荷投影变换就能得到，这实在是一件令人兴奋的简化，它似乎铺平了理解地震过程的大道。仅在Byerlee发表了岩石摩擦论文1年之后，就出现了基于这个简化假设之上的数学模型(Dieterich，1979)。这个模型建立了弹簧滑块与滑动速度之间的联系，用一个方程表达出来:

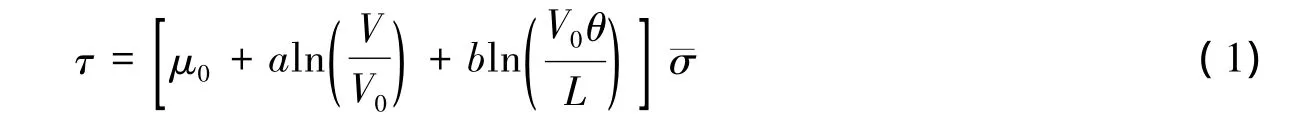
式(1)中:τ为剪应力，¯σ是有效正应力，它们都是来自于载荷的几何投影变换;a与b代表材料性质;V为滑动速度;V0为参考速度;μ0为当V=V0时的稳态摩擦系数;L为临界滑动距离;θ为状态变量。其中θ的物理意义似乎总是含混不清，经常被解释为与粗糙度、材料、滑动历史有关的变量。从量纲分析上看，这似乎应当是一个时间量。但是，它的存在对拟合实验数据显然是非常有利的。其后，这个方程被进一步推演为更为简单的形式(Ruina，1983):

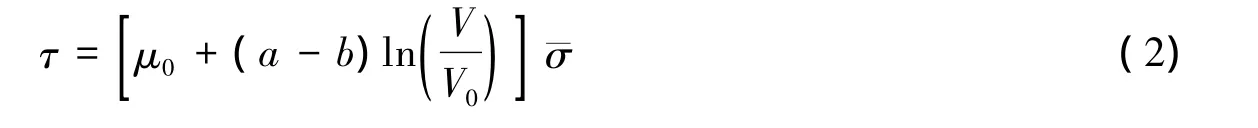
式(2)中:L与θ被简化掉了，摩擦仅仅与滑动速度相关，因此被称为速率依赖性方程。从本质上看，选择这个方程主要是因为它较好地拟合了实验数据，并非来自理论推导(Scholz，1998)。a，b及(a－b)都是来自轴向载荷与围压的测量。

几十年来，关于粘滑稳定性问题，人们已经用(a－b)的正负做过无数的讨论，发表了大量的文章。然而，我们是否注意到，如果μ0不是常数，事情会变得多么的复杂?从形式上看，当(a－b)＜0时，式(2)的速度项贡献为负，导致摩擦角变小，按照速度依赖性的理论这倾向于失稳滑动。但是实验结果表明，(a－b)的数值量级往往在千分位上(常见0.001～0.004)，而即使同种岩石在不同条件或不同滑动阶段的摩擦系数变化量也在十分位上(例如，花岗岩 0.5～0.7，辉长岩0.2～0.7)。因此，如果考虑稳态摩擦系数μ0的波动，(a－b)对摩擦角变化的贡献或者影响几乎可以忽略不计。对于一个特定的实验系统，当加载条件与样品确定之后，是否产生失稳粘滑现象已经确定，但很可能与(a－b)正负无关。这也解释了一些实验出现(a－b)明显小于零，却呈现稳滑状态的原因。事实上，Byerlee自己也多次强调，在低压情况下，受控于表面粗糙度与材料性质等因素，μ0变化很大。摩擦系数0.85对应的2kb围压所代表的低压区间大约是指地表下10km左右的范围，这里是很多活断层的运动深度，也是浅源地震的频发层位，即使是深部地震断层发生失稳错动，释放能量，也要经过这个层位到达地表。至少在这个范围上，μ0会有剧烈的变化，不仅仅在断层面的各个部位上差距悬殊，在同一部位上也会随时间发生剧烈波动。假如摩擦滑动准则真是足以判定失稳的条件，那么主导的因素只能是随时空变化的μ0。假如Byerlee给出了他的摩擦本构参数的变差值，滑动速度变化的影响将被淹没在μ0起伏的“巨浪”之中。

问题还不止于此，按照速率依赖性方程的定义，¯σ与τ是断层面的应力值，它来自实验数据，这些数据都是把轴向有效载荷用三角函数投影到预制切面的法线或者走向线方向获得的。很多实验没有在容器内部直接测量滑动带两侧的变形，地震或者粘滑释放的弹性应力被简单地认为来自加载机框架的弹性变形。这个投影能够成立的缺省假设是:岩石滑块是刚性的，沿着滑动面岩石没有变形。这在本质上已经违反了弹性回跳模型所描述的基本事实，也与多年来的地震现场考察结果不相符合。

无论数据分布有多么离散，总能获得一条趋势线来定量描述它。在工程力学问题中，出于一级近似的简单解决方法，假定滑块为刚性，可以用加载力折算断层面应力状态。如果在工程规范上必须用摩擦本构关系来表达材料的力学特性，求一个保险系数足够的近似稳定数值供工程设计使用，以估算在预期载荷作用下某种结构的稳定性，无可厚非。但是，以此为出发点建立地震预测模型，疑点甚多。首先地震断层被如何加载还是一个有待确定的学术问题，其次产生摩擦数据离散的本质原因尚未确定，离散度是多少，它带来的误差如何计算目前还不清楚。在现场观测中，实际能观测到的是局部滑动引起的断层两侧变形数据与位移数据。接受这个数据，就意味着放弃刚性块体假定;不接受这个数据就失去了推论的起点。事实上，很多场合下是在利用变形数据来推测刚性块体的加载方向，或者反之。因此，在预测模型中至少要知道这种自相矛盾的处理带来的偏差是多少。在实验中，利用速率依赖性方程计算本构参数时，往往是从刚性假定出发，计算摩擦面上的与τ，而变形却被放在远离摩擦面的压机框架上。

Brace用粘滑机制将Reid的弹性回跳理论重新焕发了生命，Byerlee用2个常数来表达地壳岩石的摩擦本构关系，用弹簧加刚性滑块模型诠释了粘滑机制。这些对后来的研究者造成了深远的影响。但是，也许我们误解了Byerlee，他在论文中强调的是摩擦问题的复杂性，特别强调低压情况下的不确定性。例如，在表示低压情况下摩擦系数分散度很大的图中，他专门标注:这里的0.85线不是平均值，不是最佳拟合数，仅仅是为了与中高压数据比较而画出的参考线。所以，Byerlee定律的准确表述应当是在低压情况下，在200MPa对应的十几km以上地壳中，μ0不是常数，不能用1条直线表达摩擦定律。如果是这样，他不给出0.85的变差量当然是合理的。事实上，Byerlee本人所建立的粘滑震源物理模型中不但没有将μ0取做常数，反而在滑动过程中设定其为波动起伏的变数(Byerlee，1970)。刚性滑块假设恐怕也是受时代技术局限的结果。30年前很少有人能够沿岩石切面对变形带进行详细的观测，对比分析与加载力之间的异同。Byerlee及那时的所有研究者都不能从围压容器内部直接测量岩石的变形，也就无从讨论断层带变形与载荷的关系。假如沿断层带的弹性变形是均匀不变的，忽略弹性回跳模型的第三要点，那么刚性假设所造成的误差是稳定的系统偏差。在缺少实验参数的情况下，刚性假设也是无奈之举。

实际测量证明，即使平滑断层滑动带两侧也具有复杂的变形模式，各个部位上都有不同的变形过程(郭玲莉，2014)。这与Reid早年所强调的完全一致。即使把各个近断层部位测量到的应力值平均，也与压机施加的载荷方向大小都不相同。这使我们不得不努力去直接获得断层摩擦滑动产生的周边变形场。深入的实验表明，粘滑的期间，断层不是仅仅完成一次简单平滑的单向错动，而是经历了复杂的多次多点震颤(李普春，2013)。我们不得不感叹，Brace早期所使用的jerky sliding motion(抽筋似的滑动)一词有多么的形象与准确。这种震源演化表现出来的时空复杂性，到高温高压的深部震源环境会加强还是减弱，有待容器内变形场的实验观测。基于震源物理过程的预报模型，应当详细地描述断层的滑动失稳时空过程，特别是由此过程中能否识别出变形进入了不可逆转的亚失稳态(卓燕群，2013)。地震的物理过程是复杂的，其预报模型必然是多参数的复杂结构，目前看不到能用一个公式表达出来的可能性。

今年是Harry Fielding Reid逝世70周年，距离他提出弹性回跳学说过去104年了。回顾历史，我们不知道该为百年来震源理论似乎没有长足的进步而惭愧，还是为Reid那穿越时空的深邃目光而折服。科学的灵魂永远是实践，弹性回跳模型的生命在于它来自对旧金山的地震考察，特别是变形场的详细测量分析(Lawson，1908)。

今年还是马瑾先生寿辰80周年，中国地震局地质研究所构造物理研究室致力于震源物理实验研究也走过了将近40年的路程。在以马瑾先生为代表的老一辈科学家带领下，研究团队坚持以中国大陆地震问题为研究方向，坚持走实验模拟与现场观测相结合的道路，获得了对震源过程的大量的新认识，同时知道了更多的未知。通过与国际上平行研究方向的历史回顾，我们汲取了经验与教训。回到经典就是回归对地震现场问题的研究，这才是正确的未来之路。

郭玲莉，刘力强.2014.区域加载过程与发震断层变形演化的实验研究［J］.地震地质，36(1):243—252.doi:10.3969/j.issn.0253－4967.2014.01.020.

GUO Ling-li，LIU Li-qiang.2014.Experimental research on regional loading process and local deformation of the seismogenic fault［J］.Seismology and Geology，36(1):243—252(in Chinese).

李普春，刘力强，郭玲莉，等.2013.粘滑过程中的多点错动［J］.地震地质，35(1):125—137.doi:10.3969/j.issn.0253－4967.2013.01.011.

LI Pu-chun，LIU Li-qiang，GUO ling-li，et al.2013.Multi-point dislocation in stick-slip process［J］.Seismology and Geology，35(1):125—137(in Chinese).

卓燕群，郭彦双，汲云涛，等.2013.平直走滑断层亚失稳状态的位移协同化特征:基于数字图像相关方法的实验研究［J］.中国科学(D 辑)，43(10):1643—1650.doi:10.1007/s11430－013－4623－4.

ZHUO Yan-qun，GUO Yan-shuang，JI Yun-tao，et al.2013.Slip synergism of planar strike-slip fault during metainstable state:Experimental research based on digital image correlation analysis［J］.Science in China(Ser D)，56:1881—1887.

Brace W F，Byerlee J D.1966.Stick slip as a mechanism for earthquakes［J］.Science，153:990—992.

Byerlee J D.1970.The mechanics of stick-slip［J］.Tectonophysics，9:475—486.

Byerlee J D.1978.Friction of rock［J］.Pure Appl Geophys，116:615—626.

Dieterich J.1979.Modeling of rock friction:Experimental results and constitutive equations［J］.J Geophys Res，84:2161—2168.

Griggs D T，Handin J.1960.Observation on fracture and a hypothesis of earthquake［A］.In:Rock deformation.Geol Soc Amer Memoir，79:347—364.

Jeffreys H.1936.Note on Fracture［A］.In:Royal Society of Edinburgh Proceedings 56，158—163.

Lawson A C.1908.The California earthquake of April 18，1906:Report of the State Earthquake Investigation Commission［R］.Carnegie Institution of Washington Publication，87(2).

Orowan E.1960.Mechanism of seismic faulting［A］.In:Rock Deformation.Geol Soc Amer Memoir 79:323—345.

Reid H F.1910.The California earthquake of April 18，1906.Volume Ⅱ.The Mechanics of the Earthquake［R］.Washington D C:Carnegie Institution of Washington Publication，87:192.

Ruina A L.1983.Slip instability and state variable friction laws［J］.J Geophys Res，88:10359—10370.

Scholz C H.1998.Earthquakes and friction laws［J］.Nature，391(1).