围压对砂砾石地基管涌影响的试验研究

杨加智，刘星星，盛金昌

(1．中国电建集团 华东勘测设计研究院有限公司，浙江 杭州 310014;2．河海大学 水利水电学院，江苏 南京 210098)

在汛期，江河堤防最常见的险情就是管涌．管涌发生时水流将携带土体颗粒不断流失，逐渐形成渗漏通道，而渗漏通道的不断发展将引起堤身下陷、不均匀沉降和整体失稳．因此，加强对管涌的研究有着十分重要的理论和现实意义．

众多学者对管涌现象做了大量的理论研究和试验验证，对管涌机理进行了深入广泛的探讨．如丁留谦等［1］通过三层堤基的管涌砂槽模型试验，分析了不同堤基结构中管涌发生、发展并导致溃堤的机理．郭书亮等［2］通过砂槽模型分析管涌发生的渗流特性并提出管涌治理方法． 但这些研究仍然主要从渗流的角度切入，很少考虑土体所处的应力状态对管涌发展的影响．近些年来，有些学者开始重视对土体应力状态的研究，如Bendahmane 等［3］设计了试验装置对罗亚尔砂和高岭土混合料在不同渗透坡降及围压的作用下的潜蚀及向后侵蚀的发展过程进行了试验研究．罗玉龙等［4］建立了渗流－侵蚀－应力耦合管涌模型，并研制了耦合装置开展试验研究．

笔者利用渗流－侵蚀－应力耦合试验装置［5］，对处于三向受压状态下的砂砾土料进行管涌研究，通过研究管涌发展过程中土体渗透系数变化、细颗粒流失情况等来揭示不同应力状态对砂砾石地基管涌的渗透变形发展过程的影响，同时也为今后考虑耦合的管涌理论研究提供一定的依据．

1 试验仪器及流程简介

试验所使用的试验装置构造如图1 所示．

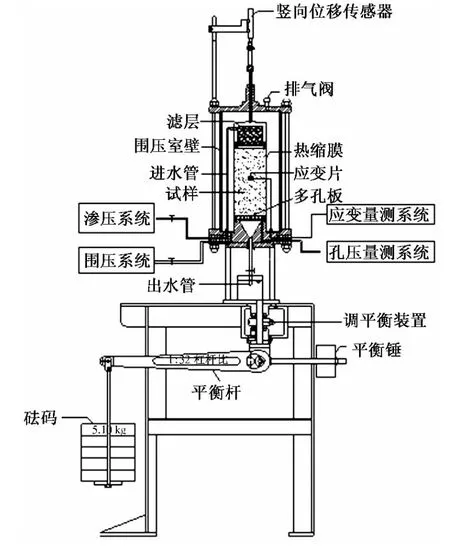
图1 渗流－侵蚀－应力耦合试验装置构造示意图

围压及轴压系统模拟土样承受三向受压状态，渗透压力系统模拟土体承受的渗流作用，数据采集系统能够实时监测土体沉降、环向应变及孔隙水压力消散等信息．

试验采用的土料级配参考Skempton 等［6］研究所用的管涌型砂砾石料A，具体试样参数见表1．试样为圆柱体，其直径(D)×高度(H)为10 cm ×10 cm．在试样制备过程中严格遵循制备流程及填筑标准．

表1 试样的物理性质指标

试验操作流程:①按规程填筑好试样，向试样中缓慢注水，待其饱和后，分级缓慢施加围压，并打开排水管固结排水;②分级施加既定渗透压力，观察渗水出口无颗粒流出及流量稳定后，测定流量，记录时间及流量，称量滤网中收集的细颗粒并记录;③试验结束后，对土样进行颗分试验，以分析土样中细颗粒的流失情况．

2 管涌试验

开展4 组试验来探究围压对管涌现象发生及发展的影响．围压分别为0．0，0．2，0．4，0．6 MPa．

2．1 不同围压作用下的试验结果

在4 组试验中，尽管渗透坡降逐渐增至足以影响大堤安全的渗流临界坡降平均值，但试样却没有出现坍塌现象．笔者选择在某次出砂持续时间较长且质量较多(占总出砂量的80%以上)时作为试验的结束，认为此时试样细颗粒流失严重，试样内部形成了渗漏通道，达到管涌破坏．

试验过程中记录了不同围压作用下的管涌临界坡降、细颗粒长时间流出时的渗透坡降、细颗粒流出的持续时间与质量、流出的细颗粒的总量及流失细颗粒的最大粒径等数据，见表2．

表2 试验数据汇总表

2．2 管涌临界坡降

经分析，发现管涌临界渗透坡降与围压呈明显线性关系，如图2 所示．由此得到不同围压状态下的管涌临界坡降icr的经验公式为

式中:P 为围压，MPa;α 与β 为拟合参数，这里α =0．71，β=0．147，其相关系数为0．984．

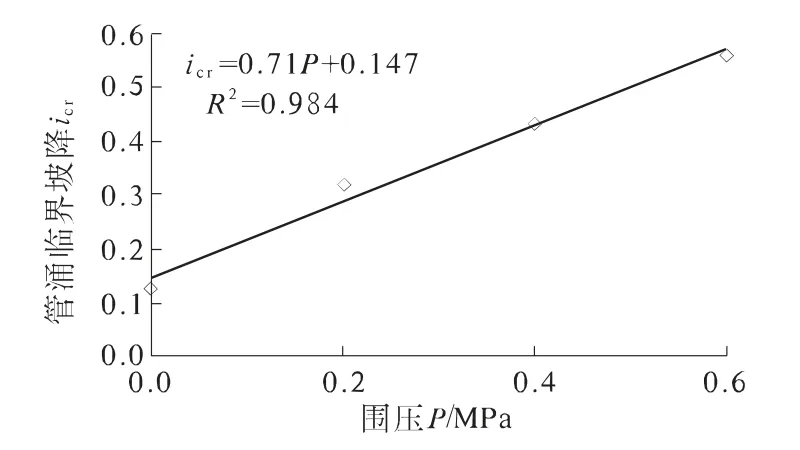
图2 围压与管涌临界渗透坡降的关系

由图2 可知，围压越大，砂砾石土体的临界渗透坡降越大，即越不容易发生渗透破坏．

2．3 围压对渗透系数的影响分析

4 组试验过程中记录的渗流速度v 与渗透坡降i 的关系如图3 所示．由图3 可以看出，随着围压的增大，v－i 曲线的斜率逐渐减小，即试样处于相同渗透坡降时，其渗透系数变小．

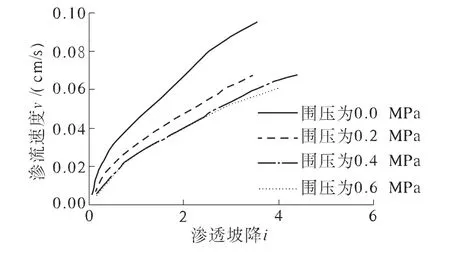
图3 不同围压状态下渗流速度与渗透坡降的关系

罗玉龙等［7］认为，在围压作用下试验得到的v－i 曲线不再满足线性Darcy 定律．土体内的颗粒可以分为骨架颗粒与可动颗粒两种，其中只有骨架颗粒能够传递有效应力．饱和向下渗流过程中，流体作用于骨架颗粒上的力包括重力、浮力和渗透力，其合力Ff方向向下，同时该骨架颗粒也会受到其他颗粒向上的作用力Fs．随着渗透坡降增加，渗透力变大，Ff值变大，当Ff＞Fs时骨架颗粒从骨架剥离后转化为可动颗粒，随着水流向下运动，此种转变反过来会影响土体应力状态，土体骨架会调整收缩，这就是渗流－侵蚀－应力耦合机制． 在骨架颗粒不断转化为可动颗粒及土体内部不断调整过程中，土体的渗透系数无法保持不变，图3 中渗流速度与渗透坡降之间的非线性趋势也证明了这一点．

在渗透坡降增加、细颗粒流失的过程中，土体内部颗粒不断调整，其渗透性时刻受到影响．这里假设在微小时段内，土体渗透性变化很小，渗流速度v 与渗透坡降i 仍满足线性Darcy 定律，即

式中k 为渗透系数．

分析处理试验数据，分别得出各围压状态下k随i 的变化曲线，如图4 所示． 由图4 可知，在试样中有细颗粒流失即管涌发生后，渗透系数急剧变低，约降为管涌开始前的1/2，而无围压施加的试样渗透系数约降为管涌开始前的1/3．同时还可以看出，围压越大，管涌发生前的土体渗透系数越小，渗透性能越低，管涌发展过程中土体的渗透性变化也越小，反映出土体越稳定．

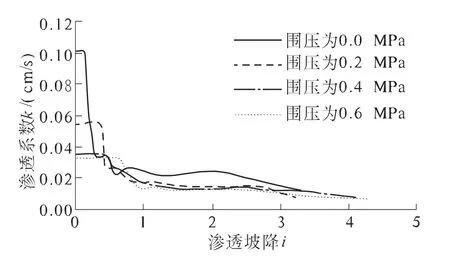
图4 不同围压作用下渗透系数与渗透坡降的关系

2．4 细颗粒流失情况

4 组试验中总的细颗粒流失情况如图5 所示．

图5 不同围压状态下出砂量与渗透坡降的关系

由图5 可知:在水力坡降达到2．5 时，4 组试样的出砂均在1．0 g 以下;当水力坡降达到3．0 以后，4 组试样出砂量都大幅增大，但是围压越大，其增幅越小．同时可以发现，施加围压的土样出砂量急剧增大时的渗透坡降较大，无围压时为3．1，而有围压状态下为4．0 左右．

对应前文k－i 图(图4)可知，在管涌发展过程中，虽然细颗粒流失量在不断增大，但渗透系数的变化速度却没有管涌开始发生时那么明显． 当每组试验结束时，出砂量均显著增加，渗透系数也明显下降，这与管涌发生时的情况相似．当可动细颗粒在水流作用下开始运移时，土体试样已经开始进行内部结构调整的过程．但是当调整很少或局部调整的时候，并不会从根本上影响反映试样宏观整体性质的渗透系数，只有当土体内的细颗粒发生大范围的颗粒调整或顺着孔隙大量涌出的时候，渗透系数才会有明显的变化，所以本试验中管涌发生及试验结束时渗透系数发生了明显的变化．

笔者认为，能随水流动的颗粒为可动颗粒，其余颗粒均视为骨架颗粒．初始渗透坡降较小时，所有颗粒均为骨架颗粒． 随着渗透坡降增大，渗透压力变大，出现Ff＞Fs，部分骨架颗粒变为可动颗粒，随着水流向下迁移．由于土体内部颗粒排布存在随机性，导致同样颗粒在不同位置受到的Fs不等，可动颗粒迁移到下游某处时很有可能出现Ff＜Fs，该颗粒又重新变回骨架颗粒． 骨架颗粒与可动颗粒的相互转化机制导致了细颗粒流失的随机性，解释了渗透坡降增大过程中细颗粒流失时快时慢、时有时无的现象．另外，随着土体的围压增大，对于处于试样内部同样位置的同一颗粒，其Fs越大，骨架颗粒越不容易转化为可动颗粒，流失的颗粒粒径上限越小．

3 结 语

1)围压对砂砾石地基的管涌临界坡降影响较为明显．管涌临界坡降icr与围压P 之间存在着显著的线性关系，具体关系见式(1)． 该公式适用于:①围压小于等于0．6 MPa;②缺乏中间级配的管涌型砂砾石地基．对于较高的土石坝工程而言，地基土体均处于较高压力状态，该经验公式不再适用，但可以推断，管涌临界坡降必将在高应力作用下显著提高．

2)围压对砂砾石土体的渗透特性影响较大:①围压越大，土体的渗透性越低． 试验中，围压为0．6 MPa时管涌发生前渗透系数仅为无围压状态下的1/3．②围压越大，管涌过程中土体渗透性的变动幅度越小，土体越稳定．

3)管涌的发生发展过程伴随着骨架颗粒与可动颗粒相互转化机制，具有一定的随机性．

4)围压对砂砾石土体管涌过程中细颗粒总流失量影响较大，围压越大，在一定的渗透坡降时，土体内细颗粒流失量越少，表明围压具有明显的遏制管涌发展的效果，且围压越大，遏制效果越明显．

［1］丁留谦，姚秋玲，孙东亚，等．三层堤基管涌砂槽模型试验研究［J］．水利水电技术，2007，38(2):19 －22．

［2］郭书亮，宿辉，张玲刚．堤基管涌模型试验研究［J］． 华北水利水电学院学报，2011，32(6):107 －109．

［3］Bendahmane F，Marot D，Alexis A．Experimental parametric study of suffusion and back erosion［J］．Journal of Geotechnical and Geoenvironmental Engineering，2008，134(1):57 －67．

［4］罗玉龙，速宝玉，盛金昌，等．对管涌机理的新认识［J］．岩土工程学报，2011，33(12):1895 －1902．

［5］罗玉龙，詹美礼，盛金昌，等．一种渗流侵蚀应力耦合管涌试验装置［P］． 中国专利:CN102411042A，2012 －04 －11．

［6］Skempton A W，Brogan J M．Experiments on piping internal stability of granular filters［J］．Canadian Geotechnical Journal，1985，22(2):215 －225．

［7］罗玉龙，吴强，詹美礼，等．考虑应力状态的悬挂式防渗墙－砂砾石地基管涌临界坡降试验研究［J］． 岩土力学，2012(S1):73 －78．