外部轴向磁场对聚能金属射流增强作用的仿真研究*

罗又天，李治源，郭春龙

(解放军军械工程学院，石家庄 050003)

0 引言

进入21世纪以来，电磁作用在战场上的运用日益增多，涉及范围也逐渐拓宽，从电磁炮到电磁装甲等各种电磁毁伤及防御的研究正在各国开展，并已取得了可观的进展，相信不久的将来，电磁武器及弹药就会装备部队。

通过研究发现，在射流外部施加轴向磁场，利用射流感应电流与外部磁场之间的电磁作用对金属射流的增强作用效果十分显著［1］。已经证实轴向外磁场作用可增长聚能射流的有效长度，从而增强其侵彻能力。

文中通过有限元软件LS-DYNA，对射流的产生过程进行了分析。而后在ANSOFT软件中建立线圈及射流的3D模型并对外磁场对射流的增强作用进行了仿真计算。通过得到的数据和结果，对这一现象进行了深入的分析，在仿真结果中得到了感应电流密度及线圈内磁场的矢量分布，并在软件中计算得到电磁力密度分布情况。通过对电磁力密度分布的分析，验证了射流在高频外磁场中增强作用，为下一步试验研究作出理论铺垫。

1 聚能金属射流的仿真计算

利用LS-DYNA对金属射流的形成及其后的拉伸进行了仿真模拟计算。由于文中并非对破甲弹射流进行具体分析研究，只需要得到射流在颈缩过程的形态及参数，所以只对破甲弹射流产生过程进行了简易的仿真。简易模型如图1所示。其中破甲弹直径设置为50 mm，药型罩的厚度为2.5 mm，顶角度数为80°。起爆方式设置为线性起爆。

图1 简易射流发生装置模型

通过仿真，得到了聚能射流的产生及拉伸的整个过程。通过对结果的分析可以得到，射流在3 μs之前并没有成型，而起初的若干微秒内，射流的拉伸及长度也增长缓慢。射流正式进入颈缩过程发生在10 μs左右，之后射流的颈缩过程逐步发展。为了使外磁场对射流的增强作用能够更加明显和有效，用于施加外磁场的驱动线圈应放置于颈缩开始后的射流颈缩部分，射流的直径大小变化显著。根据这个条件，选择在第16 μs时的射流形态为后续仿真原型，其中射流的直径1～5 mm。如图2所示。

图2 16 μs时射流形态

可以看到射流颈缩正在进行，已产生3股凸起与凹陷，粗的部分直径大致在5 mm，细的部分直径在1 mm。将驱动线圈放置于射流颈缩部分，对射流进行加强，颈缩部分长度大致为100 mm，由此可设定线圈长度为80 mm，满足覆盖颈缩部分条件，并将线圈内径大于射流凸起处半径即可。

2 金属射流轴向高频外磁场增强理论分析

2.1 射流拉伸数值模型分析

对于任何施加在射流上的基于其自然拉伸不稳定性基础上的电磁作用，都以假设出射流的物理数学模型为基础。在这个模型中，射流各部分被看成由不同半径的轴对称不可压缩的塑性圆柱体组成［2］。这个模型是基于在平截面假定的基础上:假设在任意时刻，每个延伸的圆柱体的横截面的各部分都有着相同的轴向速度。这种适当的假设可以用来解释射流在一维情况下射流表面不稳定的问题。下面列出了圆柱体的横截面轴向运动方程:

其中:z和r表示了轴向和径向的坐标;t表示时间;ρ0表示射流材料的密度;R表示圆柱体的一个截面半径;vz为给定截面的轴向速度;σz表示应力张量的轴向分量;pe表示圆柱体的表面所受压力。

根据所用材料的不可压缩性可以用来解释圆柱体在其拉伸过程中的横截面的半径变化，其公式为:

包括在式(1)中的轴向应力 σz= σz(r，z，t)是通过物理学中考虑了圆柱体的各部分轴向运动的不可压缩的刚塑性介质而被确定［3］，这时外部压力作用于圆柱体的表面。

这里介绍的简易模型可以充分的描述聚能射流的延伸。对于自然情况下，射流拉伸时的表面扰动等问题，相关文献中利用更加复杂的模型给出了类似的结果［4-6］。

2.2 高频磁场对射流增强作用原理分析

由于高频外部磁场频率较高，所以并没有穿过射流的内部。由于集肤效应的存在，感应电流以涡流的形式存在于射流的表面。对于射流来说，射流直径只有几毫米，如果磁场周期在105～106s－1甚至更小的情况下，集肤层的厚度比射流半径要低的多。则感应电流与磁场作用而产生的电磁压力，也将存在于表面层。

由于作用在射流上的电磁力可以简化为作用于射流表面的磁压力［7］，则有:

式中:Be是外部磁场对射流表面的磁感应强度;μ0是真空磁导率为1.256×10－6H/m。可以看出这里磁压力取决于射流内部磁场分布B(r，t)。在上式的基础上，由于高频情况下，内部磁场可被忽略，压力公式可被简化成:

所以射流拉伸状态下的塑性不稳定性的发展，在磁感应强度Be作用下，沿射流变形单元的长度相应的重新分配。在这种情况下，射流的突起位置受到的压力更强，而“颈缩”过程中凹陷的部分所受压力较弱，进而推迟了已形成颈缩的各单元的发展，使射流更晚的瓦解为五速度梯度的个别单元。根据计算，这种磁场作用的结果不仅增大了射流的有效长度，而且还可能改变断裂为个别单元后的射流的单元的数量。

3 有限元仿真分析

3.1 结构及仿真参数设置

由于电磁场仿真软件Ansoft可以自动考虑部件形状、相对位置及材料特性对电感等参数计算的影响，解决直接计算参数的难题。因此，文中借助电磁场有限元仿真软件Ansoft中的3D瞬态场求解器，对射流受高频外磁场作用效果进行了仿真分析。

图3 射流及线圈仿真模型

图3给出了Ansoft中建立的聚能金属射流及双层圆柱线圈的模型，其中射流形态为模拟直径为50 mm破甲弹在LS-DYNA中的仿真模型建立，材料设为铝质材料，其中颈缩部分直径为2～5 mm;双层线圈直径为20 mm和24 mm，长度为80 mm，每层线圈厚度1 mm，每层设置匝数为80;在整体外部建立空气层(图中并未体现)。网格划分过程中，对空气区域网格划分较稀疏，根据长度划分，最大长度为10 mm;双层线圈根据长度划分采取最大长度为5 mm划分;对于关键求解对象聚能金属射流采用长度划分，最大长度设为2 mm。对于仿真中全部对象在负载中考虑涡流的效果。

图4 仿真外接电路图

仿真过程中，通过外接电路的方式为驱动线圈加载，外接电路如图4。脉冲储能电容器的电压值和容量值可以根据需要设置，这里将电容器容量设为2 000 μF，电压值设为 50 000 V，线路电感设置为4 nH，等效电阻设为15 mΩ，线圈之间的连接方式为串联，仿真的起始时间为0 ms，终止时间为20 μs，仿真时间步长为1 μs。

3.2 仿真结果及分析

电流波形如图5所示。

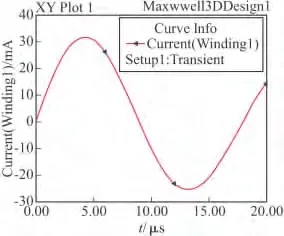
图5 电流波形图

可以看出，电流震荡单个周期为18 μs左右，电流在4.5 ～5 μs之间达到峰值，约为 3.2 ×107A。为了更好的观察高频轴向外磁场对聚能射流的增强效果，取4.8 μs时间点来分析磁场分布、射流感应电流密度分布和所受的体电磁力密度分布情况。

图6 双层圆柱线圈磁场分布矢量图

4.8 μs时的磁场分布情况如图6所示，双层圆柱线圈内部磁场分布较均匀，其中红色区域为10 T及大于10 T的磁场，橙色区域为9.2～10 T之间，在圆柱线圈两端磁场开始发散，磁感应强度较弱，最大不超过0.8 T。磁力线分布与真实螺线管产生的轴向磁场类似。

由射流外部轴向磁场分布情况及电流波形图可以看出，磁场周期在20 μs以内，双层圆柱线圈内磁场可以保证在8 T以上，满足了作为高频轴向磁场的要求。此时射流表面产生感应涡流，其电流密度分布如图7所示。

由电流密度分布矢量图可以看出，在射流颈缩开始后的凸起部分电流密度较大，局部可以达到2×1010～2.4 ×1010A/m2，而在射流凹陷部分，电流密度明显低于凸起处，只有3×109～8×109A/m2。电流的方向如局部放大图所示，设磁场正方向Z轴，则方向在XY平面上的投影为顺时针方向。由安培力计算公式:

式中:f为射流表面所受的电磁力密度分布;J为电流密度分布;B为磁感应强度。在Ansoft求解计算器中建立电磁力密度计算方程，并求解矢量图可得到射流电磁力密度分布矢量图，如图8。

图7 射流感应电流密度分布矢量图及局部放大图

图8 电磁力密度分布矢量图及局部放大图

由矢量图可以看出，电磁力密度方向沿径向向内，且分布特点与电流密度分布类似，在射流凸起部分最大，可以达到3.15×1011N/m3，而在凹陷部分，电磁力密度不超过2×1011N/m3。可以看出在高频轴向磁场的作用下，射流受到电磁力的压缩，在凸起处的压力大于凹陷处，从而使得已进入颈缩阶段的射流的颈缩发展减缓，从而有效增长射流的有效长度。

通过仿真可以看出，在当前设定条件下，电磁力集中于表面层，其作用等价于分布于射流表面的磁压力pm，使得在颈缩已经发展的部分磁压力降低，而在射流侧面凸起的区域使磁压力增大，即由强度足够大的高频磁场在射流表面凸起处对其进行压制，而在表面凹陷处则阻止其颈缩的发展。

在磁场强度10 T的情况下，得到的电磁力密度量级可达到1011量级，由于射流本身可视为半流体状态，则增强效果显著，下一步将对具体磁场对射流增强效果进行量化仿真分析，得到射流长度增长与磁场强度的关系。

4 结论

在文献［8］中，利用仿真软件通过在射流行进路径方向设置轴向磁场的方法分析了射流受外磁场作用而置稳的现象，得出了相应的射流有效长度增加的比值及磁场强度对射流的增强效果的影响等结论。

文中在国外学者研究的基础上，利用软件Ansoft对射流在高频磁场中的置稳效果进行了仿真分析。利用电容器对双层圆柱线圈脉冲放电产生轴向磁场，清晰看到了双层圆柱线圈内部磁场的分布情况，并得到了在磁场变化周期20 μs以内，场强10 T左右时，射流的电流密度分布以及计算得出的电磁力密度分布图。对射流在轴向高频磁场作用下的置稳效果进行了验证，为之后进一步分析不同场强及频率的磁场对不同形态及材料的射流的增强作用分析奠定基础。

由于破甲弹原理为爆炸压塌药型罩的方式，在炸药部分外部安装线圈，与炸药构成磁通压缩脉冲发电装置，并将用于产生轴向磁场的线圈作为负载串联于磁通压缩发电装置，由于爆炸磁通压缩装置可脉冲产生强电流，则对破甲弹射流产生增强效果的磁场电源及功率的要求被满足，具体匹配条件及参数将作为下一步研究重点。

［1］(俄)Л.П.奥尔连科.爆炸物理学［M］.孙承纬，译.北京:科学出版社，2011:1048-1060.

［2］S V Fedorov，A V Babkin，S V Ladov.Development of the magnetohydrodynamic instability of a shaped-charge jet under electrodynamics action［J］.Oboron.Tekh.，1998(1/2):49-56.

［3］A V Babkin，S V Ladov，V M Marinin，et al.Regularities of inertial stretching of shaped-charge jets in free flight［J］.Prikl Mekh Tekh Fiz，1997，38(2):3-9.

［4］P C Chou，J Carleone.The stability of shaped-charge jets［J］.Appl.Phys.，1997，48(10):4187-4194.

［5］L A Romero.The instability of rapidly stretching plastic jets［J］.Appl.Phys.，1989，65(8):3006-3016.

［6］A V Babkin，S V Ladov，V M Marinin，et al.Regularities of stretching and plastic fracture of metal shaped-charge jets［J］.Prikl.Mekh.Tekh.Fiz.，1999，40(4):25-35.

［7］S V Fedorov，A V Babkin，S V Ladov，et al.Possibilities of controlling the shaped-charge effect by electromagnetic actions［J］.Combustion，Explosion，and Shock Waves，2000，36(6):126-145.

［8］S V Fedorov.Magnetic stabilization of elongation of metal shaped charge jets［C］∥ 25th International Symposium on Ballistics Beijing，China，2010.