基于ANSOFT有限元软件的旋转磁场的仿真研究

李毓川

(中国人民大学附属中学,北京 100080)

基于ANSOFT有限元软件的旋转磁场的仿真研究

李毓川

(中国人民大学附属中学,北京 100080)

通过对“磁场”一章中恒定磁场的学习,利用磁场的数学推导和ANSOFT有限元软件,对空间中的一根导体、相互垂直的两根导体和均匀放置的三根导体中分别通入交流电流时产生的合成磁场进行了仿真计算,并对“旋转磁场”进行了模拟仿真演示,得出了一些有趣的结论。

磁场 恒定电流 恒定磁场 运动磁场 交流电 电磁场软件

ANSOFT有限元软件是一款用计算机数值模拟替代模型试验的仿真软件，它主要用于分析二维和三维的电磁部件、电气和机电设备等。它是基于麦克斯韦微分方程，采用有限元离散形式，将工程中的电磁场计算转变为矩阵求解，该分析软件已成为工程设计人员在电子产品设计中不可缺少的工具。

在人教版高中物理选修3-1课本的第3章中讲述了“磁场”的概念[1]，其中主要介绍了3种常见的磁场：通电直线导体周围的磁场、通电环形导体(环形线圈)周围的磁场和通电螺线管周围的磁场。利用右手螺旋定则和磁感线的描绘，就可以直观地表示出上述三种磁场的分布情况。总结这部分内容发现：1)课本中讲述的三种常见的磁场，均是在导体中通入恒定的直流电流产生的磁场。2)由于导体中通入的是大小恒定的直流电流，因而在任何时刻，所产生磁场中各点的磁场强度恒定不变，是不随时间改变的恒定磁场。3)课本中讲述的3种磁场在空间中是静止的、不运动的。

在现实生活中，通常使用的都是单相(或三相)交流电，如果在环形导体(环形线圈)和螺线管中通入交流电，其周围的磁场会是怎样的呢？另外，如果同时给空间排列位置不同的多个环形线圈都通入交流电，会产生怎样的磁场呢？以及如何才能产生出运动的磁场呢？

带着这些疑问和猜想，去向老师和书本请教，老师推荐了几本参考书[2，3]，建议学习和利用ANSOFT有限元电磁场分析软件[4]来仿真计算所研究磁场的分布情况。

1 一个通电环形线圈的磁场

1.1 环形线圈通直流电时的磁场

在如(图1)所示的半径为r的环形线圈中通入大小、方向都不随时间变化的恒定直流电流I，根据右手螺旋定则，线圈电流产生磁场的磁感应强度的方向垂直于线圈平面，如图1(a)所示。若磁场中材料的磁导率为μ，磁感应强度的幅值可表示为：Bm=μIm/2r。可见，此时磁场的磁感应强度幅值与线圈中电流I的大小成正比，与线圈半径r成反比。

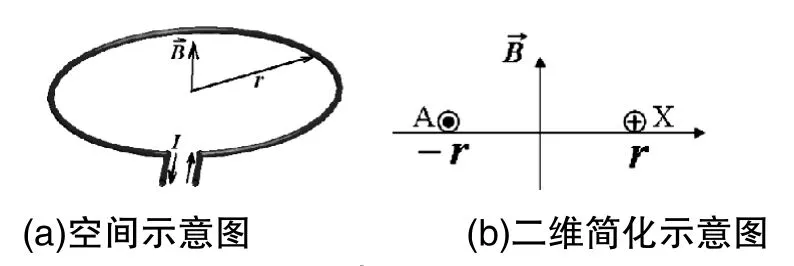
图1 通电环形线圈

对图1(a)所示环形线圈的空间示意图进行二维简化，选择横坐标轴平行于线圈平面，轴垂直于线圈平面，可得到图1(b)所示的简化示意图，其中线圈的两个横截面分别用A(线圈的首端)和X(线圈的尾端)表示，其电流方向相反，分别用○·和○+表示。

1.2 环形线圈通交流电时的磁场

如果在图1所示的半径为r的环形线圈中通入按余弦规律变化的交流电iA=Imcos(ωt)时，将产生随电流变化的磁场，其磁感应强度的幅值可表示为：

其中：Bm=μIm/2r。

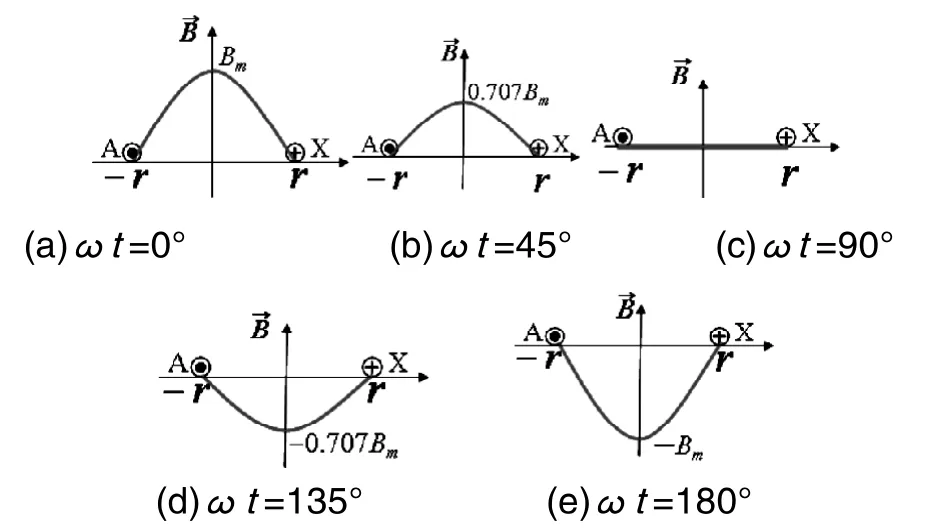
图2 通交流电的环形线圈其磁感应强度随时间变化的波形

2 通交流电的两个环形线圈的磁场

如图3(a)所示，两个完全相同的环形线圈A、B在空间中相互垂直(互差90°)，两个线圈的二维简化示意如图3(b)所示。当线圈A、B中通入幅值为Im，初相位角相差90°，角频率为ω的交流电，即iA=Imcos(ωt)，iB=Imcos(ωt 900°)时，两个线圈电流产生磁场的磁感应强度的轴线位置在空间上互差90°，各线圈磁感应强度的幅值随时间按余弦规律变化。两个线圈的磁感应强度可分别表示为：

图3 两个空间正交的通电环形线圈

两线圈合成磁场的磁感应强度为：

对式(3)，选择ωt=0°，90°，180°，270°四个时刻分别进行分析。利用图3(b)的二维简化示意图，规定线圈电流为正时，电流从线圈的首端(A、B)流出(用○·表示)，尾端(X、Y)流入(用○+表示)，反之亦然。

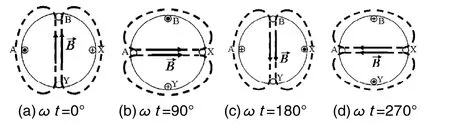
图4 两个环形线圈产生的合成磁场

当ωt=0°时，iA=Im，iB=0，将线圈电流的实际方向表示在各线圈的导体中，根据右手螺旋定则，此时两个线圈中的电流产生的合成磁场将如图4(a)所示。同理，考察ωt=90°(iA=Im，iB=0)、180°(iA=0，iB=Im)、ωt=270°(iA=Im，iB=0)时的两个线圈电流方向，可分别得到如图4(b)、4(c)和图4(d)所示的磁场分布。由图可见，当两个线圈中电流随时间连续变化时，两个线圈产生的合成磁场的轴线位置将按顺时针方向移动，即此时的合成磁场是按顺时针方向“旋转”的磁场。

利用ANSOFT有限元电磁场仿真软件对空间垂直的两个环形线圈进行建模，线圈中通入初相位互差90°、幅值为100A、频率为50Hz的交流电，在一个周期(0.02秒)内，选择不同时刻(t=0s，0.002s，0.006s，0.01s，0.012s，0.016s)绘出如图5所示的合成磁场的磁感线分布示意图，连续观察各图，可见合成磁场按顺时针方向旋转。

图5 两个环形线圈合成磁场磁感线分布示意图

3 通交流电的三个环形线圈的磁场

如(图6)所示，当空间中均匀放置三个环形线圈A、B、C，它们在空间上互差120°，假设线圈A的空间初相位为0°，则线圈B的空间初相位为-120°，线圈C的空间初相位为-240°。如果给三个线圈分别通入幅值为Im，角频率为ω，初相位互差120°的交流电，即iA=Imcos(ωt)，iB=Imcos(ωt 120°)，iC=Imcos(ωt 240°)时，三个线圈电流产生磁场的磁感应强度可分别表示为：

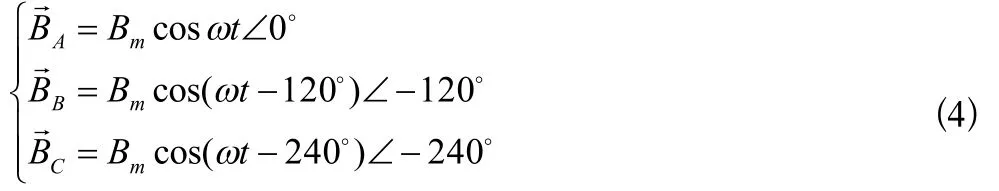
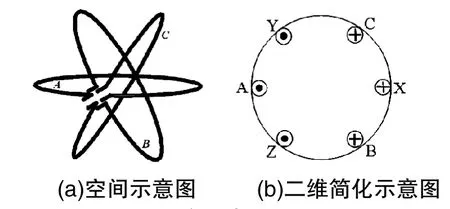
图6 三个通电环形线圈

三个线圈合成磁场的磁感应强度为：

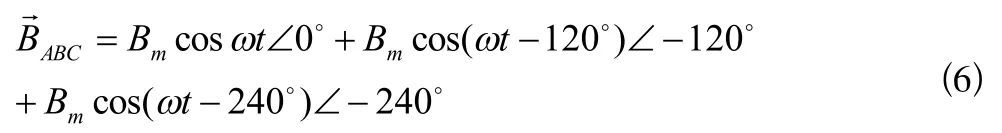
对式(6)，选择ωt=0°，ωt=120°，ωt=240°，ωt=360°四个时刻分别进行分析。利用图6(b)的二维简化示意图，按前述规定，当ωt=0°时，iA=Im，iB=iC=-0.5Im，将线圈电流的实际方向表示在各线圈的导体中，根据右手螺旋定则，三个线圈中的电流产生的合成磁场将如图7(a)所示。同理，考察ωt=120°(iA=iC=-0.5Im，iB=Im)、240°(iA=iB=-0.5Im，iC=Im)、ωt=360°(iA=Im，iB=iC=-0.5Im)时的三个线圈电流方向，可分别得到如图7(b)、7(c)和图7(a)所示的磁场分布。由图可见，当三个线圈中电流随时间连续变化时，三个线圈产生的合成磁场的轴线位置将按逆时针方向移动，即此时的合成磁场是按逆时针方向“旋转”的磁场。

图7三个环形线圈产生的旋转磁场

为了进一步验证上述合成磁场是“旋转”磁场，利用ANSOFT有限元电磁场仿真软件对空间三个环形线圈进行建模，线圈中通入初相位互差120°、幅值为100A、频率为50Hz的交流电，在一个周期(0.02秒)内，选择不同时刻(t=0s，0.004s，0.008s，0.012s，0.016s，0.02s)绘出如图8所示的合成磁场的磁感线分布示意图，连续观察图8中的各图，合成磁场按逆时针方向旋转。

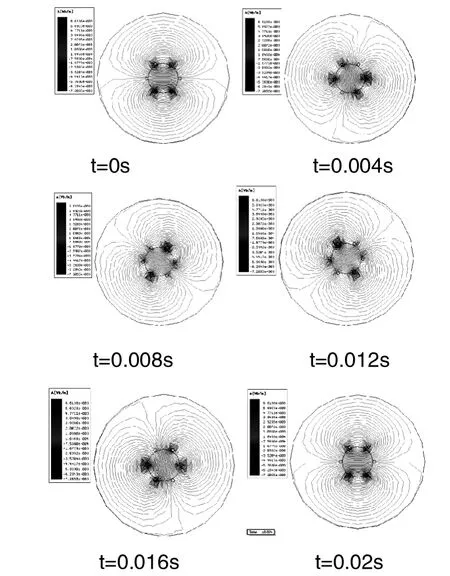
图8 三个环形线圈合成磁场的磁感线分布示意图

4 结语

本文利用磁场分布的物理表达和ANSOFT有限元电磁场软件的仿真计算两种方法，分别对一个环形线圈、空间相互垂直的两个环形线圈、空间互差120°的三个环形线圈中通入交流电流产生的磁场进行了分析，得出如下结论：

(1)当一个环形线圈中通入不随时间变化的直流电流时，磁场中各点磁感应强度的幅值恒定。

(2)当一个环形线圈中通入随时间按余弦规律变化的交流电流时，磁场中各点磁感应强度的幅值随时间按余弦规律变化，磁感应强度的方向也随电流方向的改变而变化。

(3)当给空间互差90°的两个相同的环形线圈通入幅值相同、频率相同、初相位互差90°的交流电时，两线圈的合成磁场是旋转磁场。

(4)当给空间互差120°的三个相同的环形线圈通入幅值相同、频率相同、初相位互差120°的交流电时，三个线圈的合成磁场是旋转磁场。

[1]黄恕伯,唐果南,张维善．普通高中课程标准实验教科书.物理选修3-1(第3版)[M].人民教育出版社,2012．

[2]李发海,朱东起.电机学[M],北京：科学出版社,2013．

[3]李光中,周定颐.电机及电力拖动[M].北京：机械工业出版社,2013．

[4]赵博,张洪亮.ANSOFT 12在工程电磁场中的应用[M].北京：中国水力水电出版社,2013．