The calculation method of AGN γ-ray emission flux
YANG JiangHe ,NIE JianJunYANG RuShu
(1.Department of Physics and Electronics Science,Hunan University of Arts and Science,Changde 415000,China;2.Center for Astrophysics,Guangzhou University,Guangzhou 510405,China)
The integral photons flux of celestial body emission is measured[1—7],while the emission flux density and luminosity etc.are usually adopted in a lot of investigations[8—20].Therefore,transforms the integral photons flux into other quantitative model is important to research γ-ray emissions.The conversion method will be presented in this paper.The units as cm,s,Hz,Mpc,erg,Jy and GeV are adopted,and some constants are adopted as Planck constant,h=6.626 07 × 10-34J·s,circumference ratio,π=3.141 59,luminosity distance,1 Mpc=3.085 68 × 1024cm,electron volt,1 eV=1.602 18×10-19J,and light velocity,c=2.997 92×108m/s.
1 Emission model
We assume the γ-ray photon flux associated with γ-ray photon spectrum index by a power-low spectrum[14—15,21](Fig.1),namely,

here,N is the observation γ-ray integral photon flux in units of photons·cm-2·s-1in the energy range of EL~EU(GeV),Γ the γ-ray photon spectrum index and N0the initial flux.In Figure 1,d N is the photon flux in the energy range of E~E+d E,d F is the emission total flux density in the range of E~E+d E.
From Equation(1)and Figure 1,we haveSo,N0can be expressed as
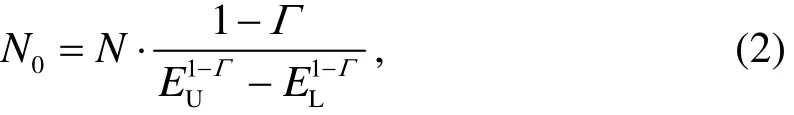
ifΓ=2,then
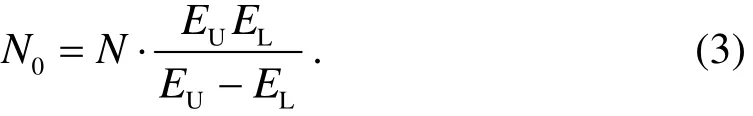
Owing to photon energy E=hv,therefore,the transform relation between photon energy(E GeV)and photon frequency(ν Hz)can be expressed as
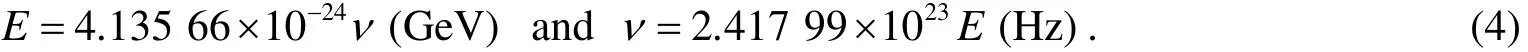
Here,the units of GeV and Hz are for photon energy E and photon frequency ν respecteviley.
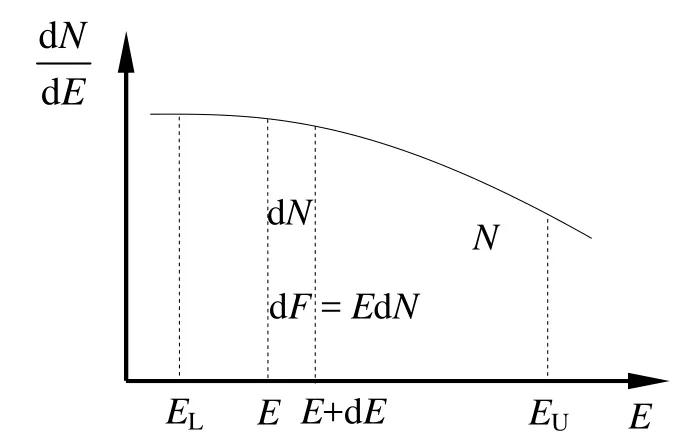
Figure 1 Emission spectrum of γ photon
2 Calculation method
2.1 γ-ray total flux,F t
From Figure 1,the emission flux in the energy range of E~E+d E is d F=E d N.So,the γ-ray total flux in range of EE d N,take into account Equation(1)
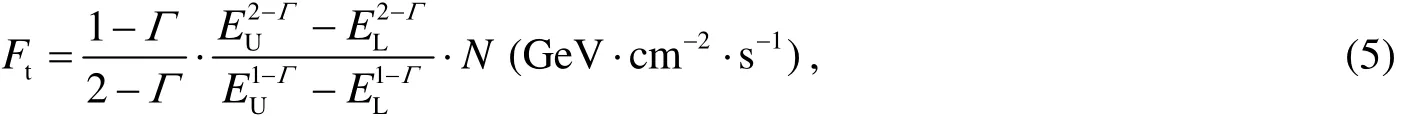
or


or
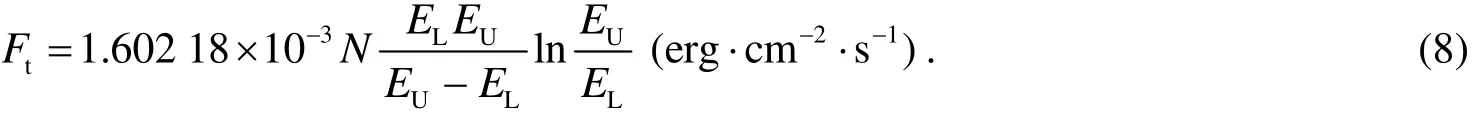
The units of N and E are photons·cm-2·s-1and GeV respectively.
2.2 Average energy of γ-photon,E a,ph
Because the γ-ray total flux(Ft)in range of EL~EUGeV is presented by Equations(5)and(7)in units of GeV·cm-2·s-1,and the observation γ-ray integral photons in the energy range of EL~EUGeV is N photons·cm-2·s-1.Therefore,the average energy of γ-photon(Ea,ph)can be calculated by Ft/N.
If 2Γ≠,then

If 2Γ=,then

2.3 Flux density at E GeV,f(E)
From Fig.1,the γ-ray flux density at E GeV(or 2.417 99×1023E Hz)can be calculated by formula,d F=E d N,and according Eq.(1),(GeV· cm-2·s-1·G e V-1).Considering 1 GeV=1.602 18× 1 0-3erg,1 Jy=1 0-23erg· cm-2·s-1·H z-1and 1 GeV⇔ 2.417 99 Hz,so,the γ-ray flux density at E GeV in units of Jy can be obtained by formula,
When Equation(2)is considered,then the flux density at E GeV is
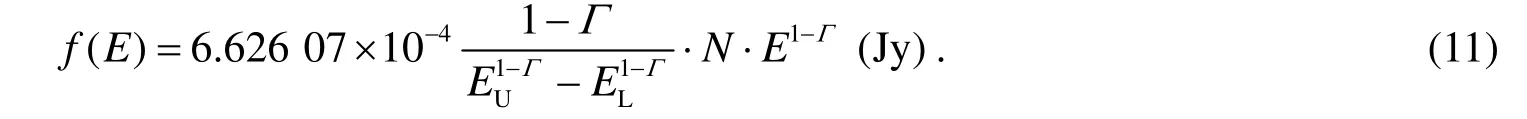
where,the units of N and E are photons·cm-2·s-1and GeV respectively.
2.4 Average flux density and its corresponding energy
2.4.1 Average flux density,fa
According to integral mean value theorem and base equation(11),we can obtained the average flux density(fa)in the energy range of EL~EUGeV by formula
If 2Γ≠,then
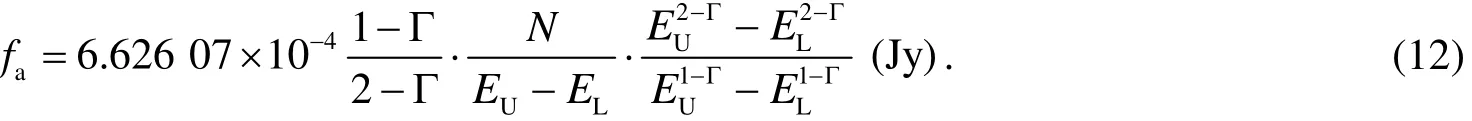
If 2Γ=,then
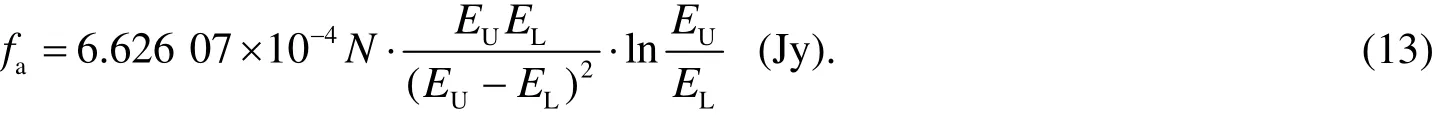
2.4.2 The corresponding energy(afE)for average flux density
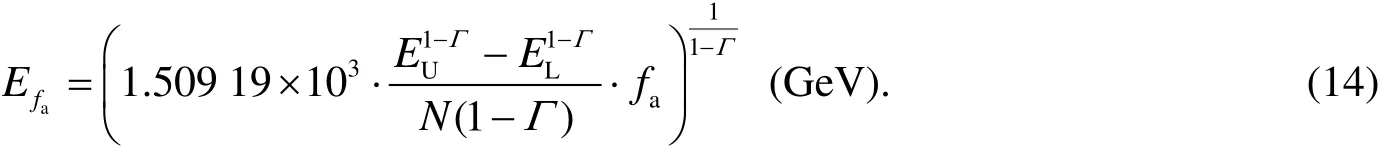
Take Equation(12)into Eq.(14),then
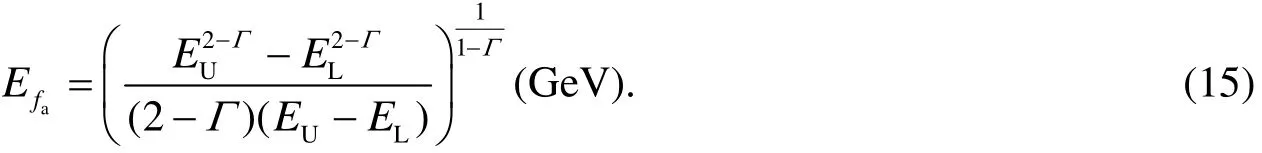
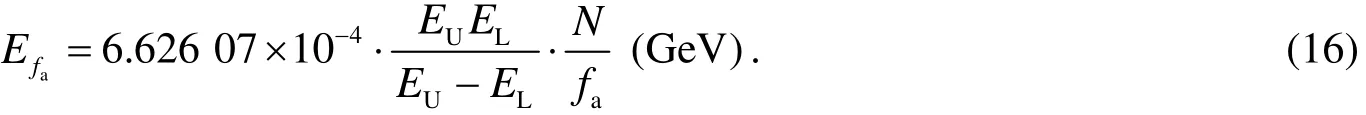
Take Equation(13)into Eq.(16),then

2.5 Luminosity
2.5.1 Total luminosity Lt
The γ-ray total luminosity in the range of EL~EUGeV is calculated by following formula,

Here,dLis luminosity distance,Ftis total flux.The units in Eq.(18)are considered,then

where,the units as Mpc is forLd,and
ifΓ≠2,and take Eq.(6)into Eq.(19),then we have,
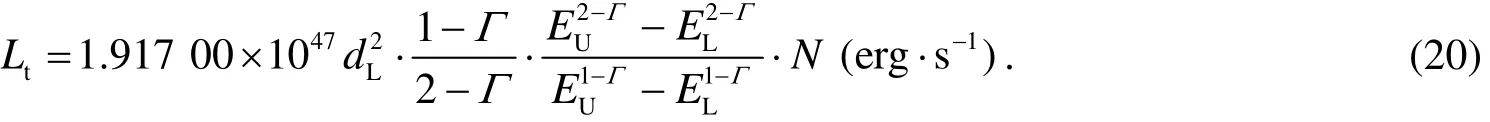
ifΓ=2,and take Eq.(8)into Eq.(19),then we have,
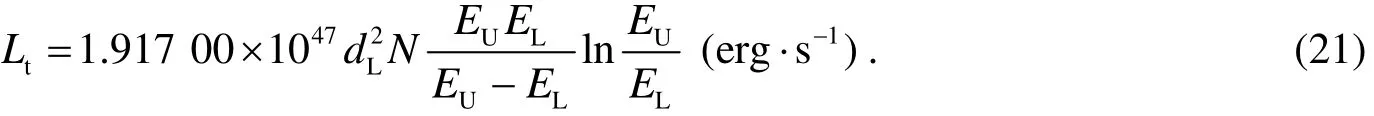
2.5.2 The luminosity at E GeV,L(E)

The γ-ray luminosity at E GeV is calculated by following formula,Here,dLis luminosity distance,f(E)is the flux density at E GeV.The units in Eq.(22)are considered,then

In which,the units of Mpc is forLd,Jy for f(E)and GeV for E.
Take Eq.(11)into Eq.(23),then we have,

2.5.3 The average luminosity,La
The γ-ray average luminosity is calculated by formula,thereinto,ν is the corresponding frequency for the average flux density,andEafis presented by Eqs.(14)~(17).When we take into account the units in the formula,
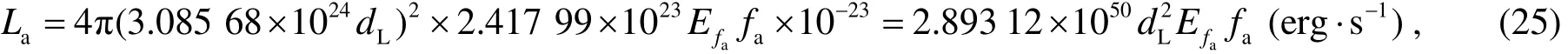
Here,the units of Mpc is forLd,Jy for faand GeV forafE .
IfΓ≠2,and take Eq.(14)into Eq.(25),then we have,
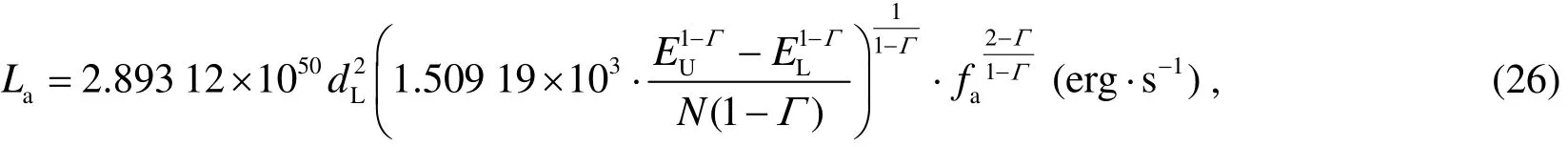
Take Eq.(12)into Eq.(26),then
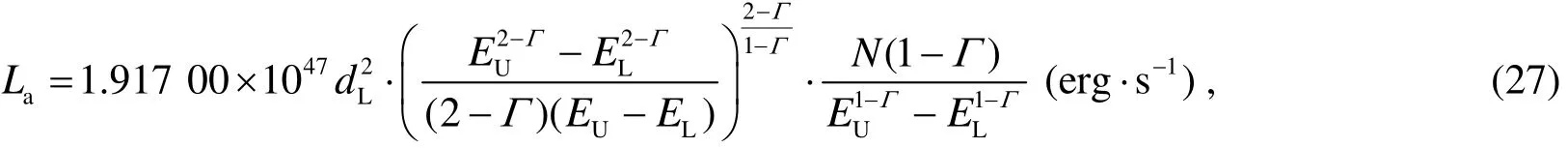
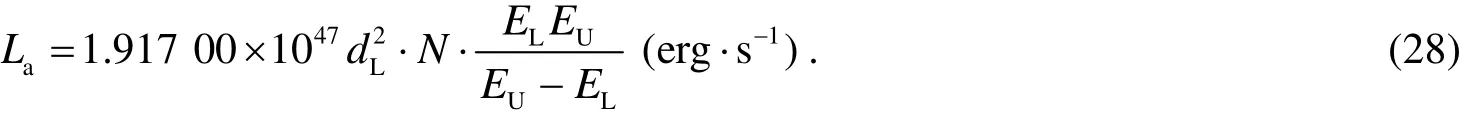
3 Example
In this paper,four blazars are selected from Femri LAT 2FGL[5—6],and listed in Table 1.In the table,z is redshift,dLis luminosity distance(Mpc)calculated by formulais the observation integral photon flux(photons·cm-2·s-1)in the energy range of 1~100 GeV,Γ is the γ-ray photon spectrum index.
The calculation results for 4 blazars are listed in Table 2.However,the results calculated in the example are not K-corrected.
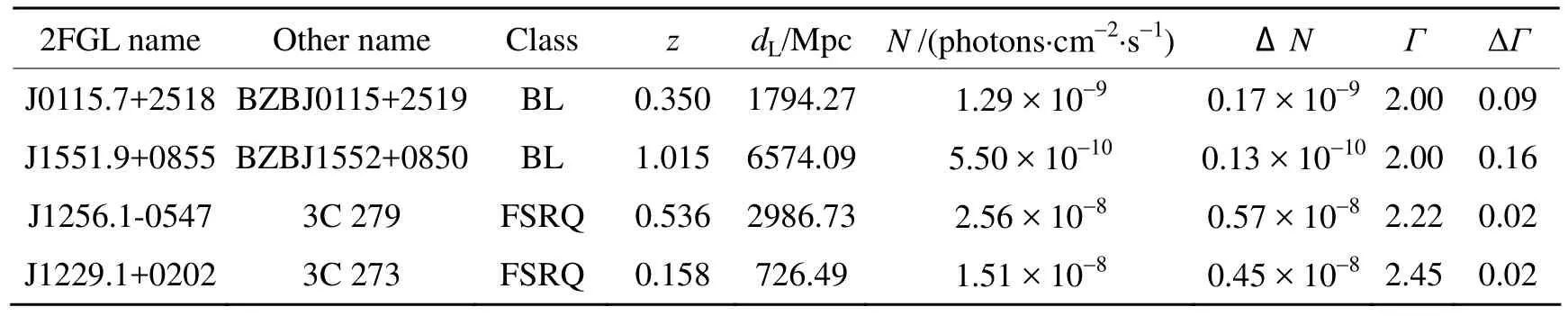
Table 1 Sample of Blazars
In Table 2,the descriptions of all columns are as follows.
Col.1,2FGL name.Col.2,Γ≠2,the γ-ray total flux(Ft/erg·cm-2·s-1)in 1~100 GeV calculated by Eq.(6).Col.3,Γ=2,the γ-ray total flux(Ft/erg·cm-2·s-1)in 1~100 GeV calculated by Eq.(8).Col.4,Γ≠2,the average energy of γ-photon(Ea,ph/GeV)calculated by Eq.(9).Col.5,Γ=2,the average energy of γ-photon(Ea,ph/GeV)calculated by Eq.(10).Col.6,the γ-ray flux density at 50 GeV in units of Jy obtained by Eq.(11).Col.7,Γ≠2,the average flux density(fa/Jy)in the energy range of 1~100 GeV obtained by Eq.(12).Col.8,Γ=2,the av er age f lux density(fa/Jy)in the energy range of 1~100 GeV obtained by Eq.(13).Col.9,2FGL name.Col.10,Γ≠2,the corresponding energy(Efa/GeV)for average flux density(fa/Jy)obtained by Eqs.(14)or(15).Col.11,Γ=2,the corresponding energy(Efa/GeV)for average flux density(fa/Jy)obtained by Eqs.(16)or(17).Col.12,Γ≠2,the γ-ray total luminosity(Lt/erg·s-1)in the range of 1~100 GeV calculated by Eq.(20).Col.13,Γ=2,the γ-ray total luminosity(Lt/erg·s-1)in the range of 1~100 GeV calculated by Eq.(21).Col.14,the γ-ray luminosity(L(50)/erg·s-1)at 50 GeV calculated by Eqs.(23)or(24).Col.15,Γ≠2,the γ-ray average luminosity(La/ erg·s-1)calculated by Eqs.(26)or(27).Col.16,Γ=2,the γ-ray average luminosity(La/ erg·s-1)calculated by Eq.(28).

Table 2 Calculation results
4 Summary
In this paper,we have discussed the calculation method of γ-ray emissions flux density,γ-ray luminosity,and average energy of γ-photons etc.using γ-ray emissions integral photons flux.The relevant volumes of the Fermi blazars emissions in a given example are calculated by the method presented in this paper.The method is also suitable in other bands such as radio,X-ray etc.,if their emissions are power-low.
[1]Abdo A A,Ackermann,M,Ajello M,et al.Fermi/Large Area Telescope Bright Gamma-Ray Source List [J].Astrophys J Sup Ser,2009,183:46—66.
[2]Abdo A A,Ackermann M,Ajello M,et al.Bright Active Galactic Nuclei Source List from the First Three Months of the Fermi Large Area Telescope All-Sky Survey [J].Astrophys J,2009,700:597—622.
[3]Abdo A A,Ackermann M,Ajello M.et al.The first catalog of active galactic nuclei detected by the Fermi large area telescope [J].Astrophys J,2010,715:429—457.
[4]Abdo A A,Ackermann M,Ajello M,et al.Fermi Large Area Telescope First Source Catalog [J].Astrophys J Sup Ser,2010,188:405—436.
[5]Ackermann M,Ajello M,Allafort A,et al.The Second Catalog of Active Galactic Nuclei Detected by the Fermi Large Area Telescope [J].Astrophys J,2011,743:171—207.
[6]Nolan P L,Abdo A A,Ackermann M,et al.Fermi Large Area Telescope Second Source Catalog [J].Astrophys J Sup Ser,2012,199:31—76.
[7]Hartman R C,Bertsch D L,Bloom S D,et al.The Third EGRET Catalog of High-Energy Gamma-Ray Sources [J].Astrophys J Sup Ser,1999,123:79—202.
[8]Dermer C D,Finke J D,Krug H,et al.Gamma-ray studies of blazars:Synchro-compton analysis of flat spectrum radio quasars [J].Astrophys J,2009,692:32—46.
[9]Fan J H,Adam G,Xie G Z,et al.Correlation between the gamma-ray and the radio emissions [J].Astron.& Astrophys,1998,338:27—30.
[10]Fan J H.Relation between BL Lacertae objects and flat-spectrum radio quasars [J].Astronphys J,2003,585:23—24.
[11]Fan J H,Yang J H,Liu Y,et al.The gamma-ray Doppler factor determinations for a Fermi blazar sample [J].Research in Astron Astrophys,2013,13:259—269.
[12]Fan J H,Yang J H,Yuan Y H,et al.The Spectral Index Properties of Fermi Blazars [J].Astrophys J,2012,761:125—136.
[13]Fan X L,Bai J M,Liu H T,et al.The connection between radio and γ-ray emission in Fermi/LAT blazers [J].Research in Astron Astrophys,2012,12:1475—1485.
[14]Fan J H,Cheng K S,Zhang L.Multi-Wavelength Variation Properties of γ-Ray-Loud Blazars [J].Publ Astron Soc Japan,2002,54:533—539.
[15]Fan J H,Yang J H,Zhang J Y,et al.Beaming Effect in Fermi Blazars [J].Publ Astron Soc Japan,2013,65:25—33.
[16]Gao X Y,Wang J C,Zhou M.External photon fields in Fermi bright blazers [J].Research in Astron Astrophys,2011,11:902—908.
[17]Singal J,Petrosian V,Ajello M.Flux and Photon Spectral Index Distributions of Fermi-LAT Blazars and Contribution to the Extragalactic Gamma-Ray Background [J].Astrophys J,2012,753:45—55.
[18]Yang J H,Fan J H,Nie J J,et al.The gamma-ray spectral index changes for blazers [J].Science China:Physics,Mechanics & Astronomy,2012,55(11):2179—2185.
[19]Yang J H,Fan J H.The correlation between gamma-ray and radio emissions in γ-ray loud blazers [J].Chin J Astron Astrophys,2005,5:229—237.
[20]Zeng H D,Yan D H,Sun Y Q,et al.γ-Ray Luminosity Function and the Contribution to Extragalactic γ-Ray Background for Fermi-detected Blazars [J].Astrophys J,2012,749:151—158.
[21]Abdo A A,Ackermann M,Ajello M,et al.Gamma-ray Light Curves and Variability of Bright Fermi-detected Blazars [J].Astrophys J,2010,722:520—542.
[22]Pedro R Capelo,Priyamvada Natarajan.How robust are the constraints on cosmology and galaxy evolution from the lens-redshift test? [J].New Journal of Physics,2007,9:445(1—30).

