批量复杂结构毛坯的快速逆向建模技术研究
王海舟 张丽艳 周良明 刘胜兰
1.南京航空航天大学,南京,210016 2.成都飞机工业(集团)有限责任公司,成都,610000
0 引言
为了提高性能、减轻重量,新型飞机中越来越多地采用钛合金整体结构件。整体结构件通常采用热等静压铸造方法获得接近设计模型的毛坯,然后对关键型面的小余量进行数控精加工以获得最终成品。然而目前飞机复杂钛合金整体铸造结构件毛坯加工定位基准的精度很难保证,且薄壁结构常常有较大变形,同一结构件的每件毛坯的实际外形均有较大的不同,从而导致后续机械加工过程中定位基准确定困难、容易出现局部加工余量不足的问题。而且,对于差异化的毛坯采用同一套数控刀轨加工,可能会产生过多空行程、加工干涉或者局部超切削深度等问题,因此需要对每件毛坯进行三维数据测量和CAD模型重建,从而针对具体毛坯进行余量分析、适应性数控编程以及加工仿真。而对批量的复杂整体结构毛坯逐件进行逆向重建,需要对每一件毛坯的测量数据都进行测量数据分块、曲面拟合、曲面处理,这些工作虽然可以通过人工交互的方法在现有的逆向工程软件中完成,但这样的重复操作会浪费大量的人力,制约生产周期。因此就提出了如何针对结构上相同、几何上彼此有一定偏差的批量实物毛坯进行高效自动化模型重建的问题。
根据实物测量数据重建CAD模型的逆向工程技术已经有了很多研究成果[1-4]。本文主要针对批量的复杂结构毛坯逆向重建中的数据分割和曲面重建开展自动化、智能化方法的研究。已有研究中对于点云的分块算法主要有基于边的方法[5]、基于面的方法[6]和将二者结合的方法[7],近年来也有一些基于八叉树空间拓扑结构的分块方法[8],文献[9]提出了在被测对象的线框模型引导下进行测量数据分割的方法。然而,对复杂的包含多种曲面类型的测量数据,上述方法均很难自动完成与设计意图相符的分割。
本文针对复杂整体结构毛坯测量数据的结构特点,结合基于面的分割方法,提出了一种结构特征模板引导下的点云分割方法,有效解决了基于面的分割方法对于“种子点”难以获取的问题,能够在实物具有较大程度变形的情况下完成不同类型特征的数据自动分块。在点云分割好的基础上,通过读取和解析基于开放式知识表示的逆向设计表,达到曲面快速重建的目的。该方法已在CATIA/CAA平台上实现,并进行了实验验证。
1 批量毛坯快速逆向建模的方法策略
对于单个毛坯测量数据的CAD模型重建,常规的方法流程如图1所示,整个过程需要大量的人工参与,对于批量毛坯则需要不断重复类似的重建过程。本文根据批量毛坯具有相同结构特征的特点,设计了一条基于毛坯结构特征模板和逆向设计表的快速逆向建模技术路线,如图2所示。

图1 单件毛坯逆向建模流程图
该方法通过事先一次性定义的结构特征模板引导自动化处理程序对每一件毛坯的测量数据完成结构分割,得到相同拓扑结构的分块数据。创建的逆向设计表通过开放式的知识表达语言固化了批量毛坯的逆向建模流程,通过对这一固化流程的自动解析,自动重建算法根据每件具体毛坯的分块数据自动完成其模型的重建,重建出的毛坯模型既具有相同拓扑结构又忠实于实测数据几何形状。上述思路已经利用CATIA/CAA二次开发技术,在CATIA环境下编程实现。
2 结构特征模板与逆向设计表
2.1 结构特征模板的创建

图2 批量毛坯快速建模流程图
一般来说,工程实际中的毛坯都有对应的设计数模,如图3所示。毛坯设计数模和需要重建的毛坯CAD模型在外观上是相似的,只是由于工艺因素不同,外形上会有一定的偏差。将毛坯设计数模与实时模型对齐,则设计数模上的每个面对应点云数据的一部分。在已有的相关研究中,对齐可以通过简单的“321”法、选取对应的三点法、PCA(主分量分析)法等来实现。本文主要参考文献[10]的方法应用遗传算法寻最优解,从而实现毛坯结构数模与实测模型的精确对齐。
设计数模中的面按结构类型可分为:平面、二次曲面、规则型扫掠曲面、自由曲面、过渡曲面等。图3所示毛坯就包括平面、圆柱面、规则型扫掠曲面和过渡曲面4个类型,这些面即是在逆向建模中需要重建的面,分别代表了毛坯每一部分的结构特征。根据不同曲面的类型,选取其上的一个或多个点作为对该面进行分块的引导点,经过曲面分类的设计数模和这些引导点以及用于后续自动模型重建的一些交互生成的辅助点、辅助面等共同构成结构特征模板文件,结构模板上的引导点对应于毛坯测量数据上的一片区域,也就是重建后模型的每个型面。

图3 毛坯测量模型与设计数模
2.2 基于开放式知识表示的逆向设计表
本文根据知识的开放式表示方法创建逆向设计表,这种方式方便用户理解和维护表中的知识,使用户能够根据不同的毛坯结构和重建过程灵活编写可以被程序自动解析的逆向设计表。设计表的BNF(backus-naur form)范式表示如下:

从表达式可以看出,输入变量可以为一个或多个,输出结果为一个变量。操作子集合包含系统提供的所有面向用户的逆向建模函数功能。每个操作子均隐含了相应的变量个数,变量的具体内容(如点的坐标)来自于结构特征模板。这样的设计规范方便逆向模型的设计和操作人员自行完成设计表的理解与编写工作,而且可以根据不同的毛坯模型不断地改进完善,达到预期的效果,如图4所示。
3 点云数据分块
数据分块就是将整体外形数据分解为若干对应实物样件上不同曲面的分块数据集,它是特征分解重建的基础。本文主要采取基于面的方法进行数据分块,首先计算整个点云数据中所有点的法矢,然后通过结构特征模板中代表不同点云数据区域的引导点寻找其对应区域的最近点作为“种子点”,再以“种子点”为中心,向外搜索周围点法矢与种子点法矢的偏差在一定阈值范围内的点,完成区域生长过程,从而实现对点云数据的分割,分割算法基本流程如图5所示。

图5 点云分割算法流程图
3.1 平面类型点云分块
平面类型点云分块是最简单也是最基础的点云分块类型,本文采取判断“种子点”与周围点的法矢是否接近平行的方法来分块。该方法对应设计表中的操作子为“PlaneCloudDevide”,由“引导点”按照图5所示的流程进行生长,直到将所有满足法矢向量与种子点法矢向量之间夹角小于一定阈值(即接近平行)要求的点全部分割完毕,得到分割结果如图6所示。

图6 平面点云分块示例
3.2 圆柱面类型点云分块
文献[11]提出了一种判断点的法矢与圆柱轴线是否接近垂直的参数化方法,该方法成功地在测量数据中提取出了圆柱点云。本文则在此方法基础上附加半径阈值条件,使得圆柱面点云分块更加准确、可靠,对应逆向设计表中的操作子为“CylinderCloudDevide”。
首先根据两个引导点分别寻找毛坯测量数据上距离它们最近的两点A和B,计算这两个点的法矢na和nb并做叉积no=na×nb,向量no即为圆柱的大致轴线方向。过点A作垂直于向量no的平面Pa,将另一点B的法矢向量nb投影到平面Pa上,将投影之后的向量n′b与点A 的法矢na延伸并相交于一点O。该交点O到A的距离OA就大致为圆柱的半径长度,点O和向量no就确定了圆柱轴线OC的大致位置,如图7a所示。再由种子点A向外进行生长,将生长点I的法矢ni与垂直向量no作点积n′i=ni·no,如果n′i小于一定的阈值要求(即ni和no接近垂直),且生长点I到圆柱的大致轴线OC 的距离O′I满足O′I≤(OA+n),其中,n为设定的阈值,则将点I加入到当前的圆柱点云分割数据集当中,直至完成整个圆柱面点云的分割,如图7b所示。

图7 圆柱面点云分块示例
3.3 其他曲面类型点云分块
毛坯中的自由曲面一般都包含尖锐边界,在同一数据域的点云范围内,相邻点之间的法矢夹角较小,而在不同数据域上的相邻点之间法矢夹角较大,因此计算出相邻点的法矢夹角,通过比较法矢夹角就能够检测出数据边界,确定自由曲面对应的点云数据。
过渡曲面部分对应的点云区域常常是面与面之间的倒角部分,这部分点云数据曲率变化较大,相邻点之间的法矢夹角变化缓慢,通过法矢准则很难将其正确地识别出来。因此本文将基本类型的曲面点云数据分割完毕后,不对此部分点云数据进行划分,过渡部分的曲面重建则是在对各基本曲面重建之后通过计算倒角半径在已有模型上正向创建。
4 不同曲面特征的自动重建
4.1 不同曲面特征的拟合
本文对于平面和圆柱面的拟合主要采取最小二乘法,这种方法在文献[12-13]中已经介绍得很详细,对应逆向设计表中的操作子分别为“Fit-Plane”、“FitCylinder”。对于自由曲面的重建,借助于CATIA/CAA平台上拉伸或者扫掠等曲面生成方法的接口函数构造自由曲面。以基于多截面线的曲面自动重建方法“Mul_SectionSurface”为例,首先得到在结构上与网格数据相垂直的已经拟合完成的平面,将该平面沿法线方向偏移一段距离,用偏移后的平面作为截平面去和点云数据的三角网格求交,获得三角网格数据上的任意一个三角网格与截平面的两个交点,并将该两个交点作为起点,再以这个三角网格为起始三角网格逐次判断相邻的三角网格是否与截平面相交,如果相交则将交点加入交点集合,如不相交则结束。最后获得了一组排序好的点集合,利用这组点拟合样条曲线。同理生成多条截面线,再利用这组样条截面线拟合生成满足条件的样条曲面。
4.2 曲面特征的后处理

图8 未进行后处理的曲面模型
前面的点云分块与曲面特征拟合操作之后得到的是一个个单独的曲面特征,如图8所示。为了得到最终完整的CAD模型,需要对这些单独的曲面特征做进一步处理操作。例如:将曲面提取边界线并进行延伸“Extend”、曲面之间的结合“Join”、曲面求交“Intersect”、依据轮廓线裁剪曲面“Splite”、用基准平面裁剪曲面“Trim”、曲面之间的桥接“Blend”等。以图9所示的裁剪曲面为例,首先将待处理平面以及与其相邻的4个平面分别进行延伸,其次将相邻的4个平面分别依据基准平面相互进行裁剪,并将裁剪后的4个平面结合,然后将结合曲面与待处理的平面进行求交,获得裁剪所需的轮廓曲线,最后将待处理平面依据轮廓曲线进行裁剪,得到最终的裁剪平面,如图10所示。

图9 毛坯模型中待裁剪的曲面示例

图10 重建后的曲面处理示例
对于模型中的倒角、圆角等过渡特征部分的重建,本文采用的方法是在重建主要特征之后,通过提取过渡特征的关键参数(如圆角半径),在已有的曲面模型上正向创建。例如在两平面特征之间创建倒角,对应逆向设计表中的操作子为“Fillet”,通过法平面和过渡部分的点云测量数据求交,提取这些交线圆弧部分的曲率半径并求平均值,通过得到的半径平均值对两平面进行倒圆角,如图11所示。
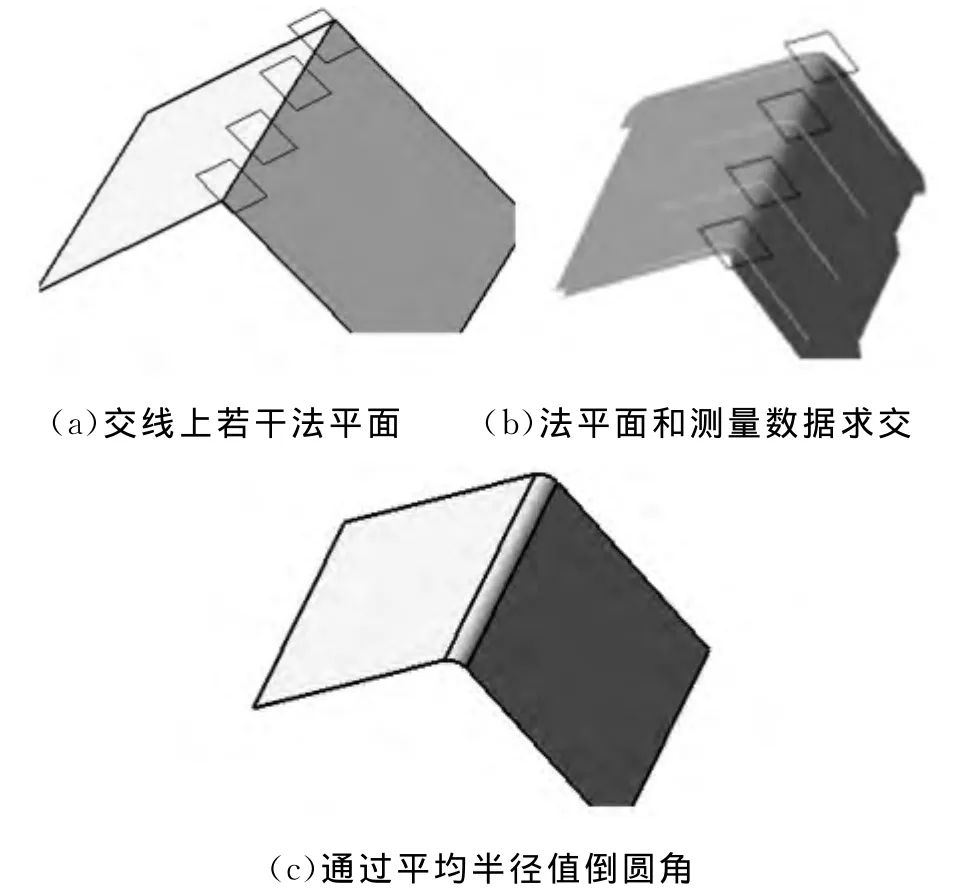
图11 两平面间倒圆角示例
4.3 曲面重建结果与精度分析

图12 重建后的CAD模型与测量数据
图12给出了应用本文方法得到的两个毛坯重建模型与各自原始测量点云的重叠显示结果。图12a中的测量数据不是实际测量所得的,而是根据设计数模在CATIA系统中模拟创建毛坯数模,再将该毛坯数模离散为三角网格模型来模拟实际测量得到的毛坯数据,得到的网格数据较为光滑。用Imageware软件对该模拟毛坯模型的曲面重建偏差进行分析,结果显示偏差在0.2mm以内,而倒角处由于采取通过对点云数据的分析和过渡半径提取创建而成,所以重建偏差较大,达到了0.4mm,整个重建CAD模型与模拟测量三角网格模型之间的平均偏差在0.05mm左右。图12b中结构件毛坯的测量数据由ATOSII流动式光学测量系统实际测量所得,由于是待加工毛坯件,因此表面粗糙度较大。精度分析的结果显示的是在边界处偏差较大,这是由于毛坯样件棱角处受到摩擦而产生了不均匀的变形,而重建后的CAD模型棱角处较为尖锐。重建后的整体曲面模型与毛坯测量数据之间的平均偏差为0.65mm,能够较好地满足工程实际应用要求。
5 结语
针对批量复杂结构毛坯的快速逆向建模问题,本文提出了一种基于结构特征模板和逆向设计表的快速逆向建模方法。该方法用一次创建的结构特征模板代替人工逆向建模过程中针对每一件毛坯测量数据的人工规划,并用逆向设计表来表达逆向建模流程。本文提出的方法应用于工程实例中取得了良好的模型重建效果,且相比于传统方法大大提高了批量毛坯的模型重建效率。
[1]Varady T,Martin R,Cox J.Reverse Engineering of Geometric Models-an Introduction[J].Computer-aided Design,1997,29(4):255-268.
[2]金涛,陈建良,童水光.逆向工程技术研究进展[J].中国机械工程,2002,13(16):1430-1436.Jin Tao,Chen Jianliang,Tong Shuiguang.A Review of Reverse Engineering Technology[J].China Mechanical Engineering,2002,13(16):1430-1436.
[3]Paolo T,Marco T,Bart D B,et al.Empirical Studies in Reverse Engineering:State of the Art and Future Trends[J].Empirical Software Engineering,2007,12(5):551-571.
[4]Maura M,Michele G.Reverse Engineering and Restyling of Aesthetic Products Based on Sketches Interpretation[J].Research in Engineering Design,2009,20(2):79-96.
[5]刘胜兰,周儒荣,张丽艳.三角网格模型的特征线提取[J].计算机辅助设计与图形学学报,2003,15(4):444-448.Liu Shenglan,Zhou Rurong,Zhang Liyan.Feature Line Extraction from Triangular Mesh Model[J].Journal of Computer Aided Design &Computer Graphics,2003,15(4):444-448.
[6]Besl P J,Jain R C.Segmentation Through Variableorder Surface Fitting[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1988,10(2):167-192.
[7]Yokoya N,Levine M D.Range Image Segmentation Based on Differential Geometry:a Hybrid Approach[J].IEEE Transcation on Pattern Analysis and Machine Interlligence,1989,11(6):644-649.
[8]Miao Wang,Yi Hsing Tseng.Incremental Segmentation of Lidar Point Clouds with An Octree-structured Voxel Space[J].Photogrammetric Record,2011,26:32-57.
[9]程云勇,张定华,张顺利,等.CAD模型引导的涡轮叶片密集测量数据分割[J].中国机械工程,2009,20(18):2214-2218.Cheng Yunyong,Zhang Dinghua,Zhang Shunli,et al.A CAD Model Directing Method for Turbine Blade Density Measurement Data Segmentation[J].China Mechanical Engineering,2009,20(18):2214-2218.
[10]严思杰,周云飞,彭芳瑜,等.大型复杂曲面加工工件定位问题研究[J].中国机械工程,2003,14(9):737-740.Yan Sijie,Zhou Yunfei,Peng Fangyu,et al.Research on Localization of the Workpieces with Large Sculptured Surfaces[J].China Mechanical Engineering,2003,14(9):737-740.
[11]Schnabel R,Wahl R,Klein R.Efficient RANSAC for Point-cloud Shape Detection[J].Computer Graphics Forum,2007,26(2):214-226.
[12]官云兰,程效军,施贵刚.一种稳健的点云数据平面拟合方法[J].同济大学学报(自然科学版),2008,36(7):981-984.Guan Yunlan,Cheng Xiaojun,Shi Guigang.A Robust Method for Fitting a Plane to Point Clouds[J].Journal of Tongji University(Natural Science),2008,36(7):981-984.
[13]曲学军,杨亚文,韩志仁.基于散乱数据表面法矢的二次曲面拟合[J].航空学报,2007,28(4):1018-1024.Qu Xuejun,Yang Yawen,Han Zhiren.Quadric Surface Direct Fitting Based on Normal Vectors of Random Data[J].Acta Aeronautica et Astronautica Sinica,2007,28(4):1018-1024.

