丘陵和平原地区表孔水工闸门波浪要素计算方法

祝凤山，杜培文，房金贤

(1.山东省水利勘测设计院水工机械设计室，济南 250013;2.山东水总机械工程有限公司研发部，济南 250100)

1 研究背景

《水利水电工程钢闸门设计规范》中规定设计水头下、校核水头下的波浪压力是水工金属结构设计中必须考虑的荷载之一［1］，波浪要素的计算正确与否，将直接影响着波浪压力的计算结果和工程运行安全。波浪要素主要包括平均波长、平均波高、波周期、波浪压力等。据统计，国内外波浪要素的计算方法有官厅水库公式、史蒂文生公式、安德烈扬诺夫公式、西晓夫公式、莆田试验站公式、鹤地水库公式等［2］几十种，因各种计算公式考虑因素的差异，使得它们的适用范围和计算精度出入很大。《水利水电工程钢闸门设计规范》中指出波浪压力的计算“按现行《混凝土重力坝设计规范》所列公式或按浅水波计算方法进行计算。”［1］目前国内多采用莆田试验站公式、鹤地水库公式和官厅水库公式计算波浪要素。针对丘陵和平原地区的水闸，《混凝土重力坝设计规范》(SL319)推荐采用鹤地水库公式计算波浪要素［3］。

程兴奇等［4］对水工建筑物波浪要素的计算进行了探讨，提出了计算简单方便的简化公式，并给出了某丘陵地区水库的算例;苗兴皓等［5］利用 Visual C++对莆田试验站公式进行了程序计算，并通过工程实例进行了验证。上述方法多采用假设、逐步逼近法、迭代法等，计算繁琐且存在误差。传统的闸门荷载计算，通常将波浪压力与静水压力等荷载叠加，其作用点位置采用静水压力作用点位置，计算不准确，误差大。围绕水工闸门波浪要素计算存在的问题，本文利用MathCAD Prime 2.0软件［2］给出了计算简便、结果准确的丘陵和平原地区表孔水工闸门波浪要素中的平均波高hm的计算方法，并给出了表孔水工闸门波浪压力、作用点位置的计算公式，该方法同样适用于相同工况下的其它水工建筑物的波浪要素计算。

2 鹤地水库公式

对于丘陵、平原地区水库，库水较深、计算风速v0＜26.5 m/s及风区长度(有效吹程)D ＜7.5 km时，采用鹤地水库公式，即

式中:g为重力加速度，g=9.81 m/s2;h2%为累积频率2%的波高(m);D为风区长度(m);v0为计算风速(m/s);Lm为平均波长(m)。

3 波浪压力公式

根据混凝土重力坝设计规范(SL319)的计算方法，作用在水工闸门上的波浪压力，应根据闸门前水头(水域平均深度)Hm与使波浪破碎的临界水深Hcr、平均波长Lm的关系，按以下2种波态分别计算。

(1)当Hm≥Hcr且Hm≥Lm/2时，波浪压力计算公式为

式中:Hm为闸门前水头(m);Hcr为使波浪破碎的临界水深(m);Pwk为单位长度迎水面的波浪压力(kN/m);h1%为累积频率1%的波高(m);γ为水的重度(kN/m3);hz为波浪中心线至计算水位(闸前水头)的高度(m)，计算公式如下:

(2)当Hm≥Hcr且Hm＜Lm/2时，波浪压力计算公式为

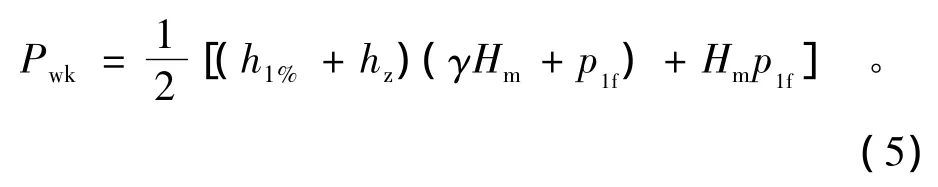
式中:p1f为水工闸门底面处的剩余浪压力强度(kN/m2)，其计算公式为

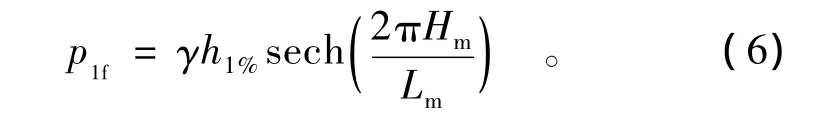
4 波浪要素的计算

已知闸门前水头Hm，且通过鹤地水库公式，可计算出累积频率为2%的波高，通过表1“不同累积频率为P(%)的波高hp与平均波高hm的比值”进行换算平均波高hm，进而求得累积频率1%的波高h1%。

从表1可知，累积频率为2%的波高h2%与平均波高 hm的比值 h2%/hm∈［1.56，2.23］，则能得出平均波高 hm∈［h2%/2.23，h2%/1.56］。本文以 Math-CAD为计算工具，求出准确的平均波高。

以表1的第1列、第3列、第4列建立计算矩阵M。

以待求的平均波高 hm为自变量 x，令 y=h2%/x，在矩阵 M 中，利用 MathCAD自定义函数f(y)对矩阵第2列插值(对应表1的第3列)，下面程序显示的MathCAD自定义函数f(y)所示，求得其对应的hm/Hm的值，即函数f(y)的返回值。

令:g(x)=f(h2%/x)－x/Hm，可以得出:以 x为变量，包含累积频率为2%的波高h2%、闸门前水头Hm等已知条件的函数曲线。当 g(x)=0时，f(h2%/x)=x/Hm，即函数曲线与横坐标的交点坐标为平均波高hm的值，如图1所示。

函数 g(x)可通过MathCAD内置函数［6］求得其与横坐标的交点坐标，即解出平均波高hm，其表达式为:hm=root(g(x)，x， h2%/2.23，h2%/1.56)。

图1 累积频率为2%的波高h2%、平均水深 Hm和平均波高x的函数曲线Fig.1 Functional curve of wave height h2%(cumulative frequency 2%)，average water depth Hm，and mean wave height x

在矩阵M中，对第1列(对应表1的第3列)插值求得累积频率为1%的波高h1%，代入式(3)或式(4)后，求得波浪压力。

5 闸门波浪压力及作用点位置的计算

依据《水利水电工程钢闸门设计规范》，表孔闸门顶部应有0.3 ～0.5 m的超高［1］，对于风浪下挡水闸门来讲，超过闸门高度的波浪越过门顶，闸门荷载计算时超过门顶的波浪压力不予考虑。以水压方向为x轴、表孔闸门铅垂方向为y轴建立直角坐标系，假设门顶超高为0.5 m。

表1 不同累积频率P的波高hp与平均波高hm的比值Table 1 Ratio of wave height hpto mean wave height hmin the presence of different cumulative frequencies P

令:

静水压力线 j1(x)=Hm－x;

闸门门顶高度线 j2(x)=Hm+0.5;

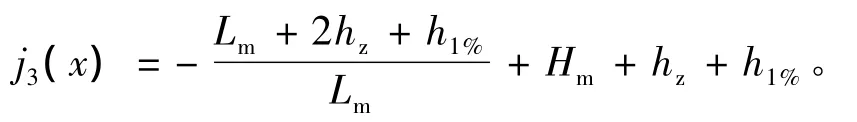
波浪作用线静水压力线、闸门门顶高度线、波浪作用线在坐标系中的图形如图2所示。超过闸门门顶高度线j2(x)的波浪压力不予考虑，则单位长度作用在闸门上的波浪压力为 j1(x)与 j2(x)，j3(x)，y轴围成的四边形图形的面积。

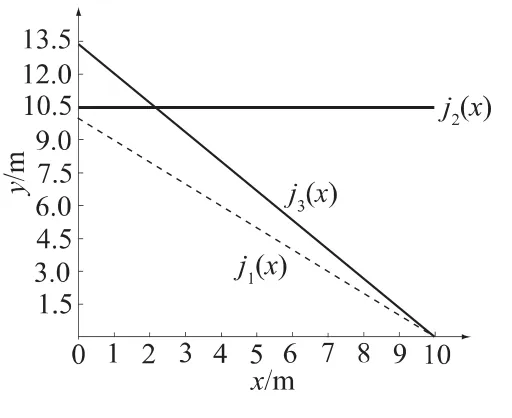
图2 单位长度内闸门波浪压力的几何表示Fig.2 Geometric figure of wave pressure in unit length

求得:j2(x)，j3(x)交点坐标为(x1，y1);j1(x)，j3(x)交点坐标为(x2，y2)，可求出单位长度作用在闸门上的波浪压力为

该四边形为均质四边形，其质心即为波浪压力的中心位置，利用双重积分［7］可求得其质心的位置坐标(x3，y3)，其数学计算结果如下。

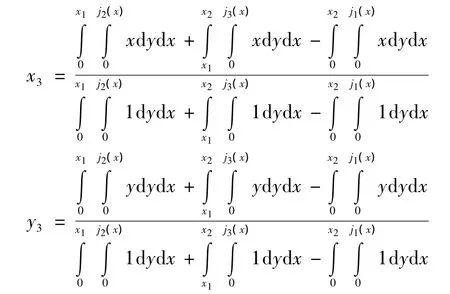
将波浪压力列入闸门荷载时，其作用点距闸室底板的高度hwz为质心纵坐标y3的值。

6 算例

以程兴奇［4］在《水工建筑物波浪要素计算探讨》中的某水库为例，水域平均深度为10 m，计算风速为20 m/s，风区长度为6 000 m，采用鹤地水库公式计算，计算结果见表2。

(1)按照式(2)进行计算，Lm=19.096 m;按照式(1)进行计算，h2%=2.217 m。

(2)按照本文给出的计算方法，得到 hm=1.065 m，与文献［4］提出的《土石坝规范》方法、《荷载规范》方法分别计算得出的hm=0.99 m和hm=1.074 m相比，计算绝对精度分别提高了75，10 mm，相对精度分别提高了7.5%，1%;累积频率为1%的波高 h1%=2.395 m。

(3)水库设表孔闸门，按照闸门挡水高度为10 m、闸门超高0.5 m计算，其单位宽度的波浪压力pwk=129.63 kN/m，波浪压力作用点位置距闸室底板高度 hwz=7.12 m。

表2 波浪要素计算结果Table 2 Calculated results of wave factor

7 结论

(1)本文利用MathCAD软件给出了方便简单、结果准确的求解丘陵和平原地区表孔闸门平均波高hm的计算方法、波浪压力作用点位置的计算公式，可适用于相同工况下的水工建筑物的波浪要素计算。

(2)计算丘陵和平原地区表孔闸门的波浪压力时，除依据《混凝土重力坝设计规范》规定的波浪要素与闸门前水头Hm的关系分2种波态进行计算之外，还应依据闸门高度进行综合计算。

(3)计算闸门包含波浪压力在内的各荷载组合时，要综合计算波浪压力的大小和作用点位置，设计时应引起重视。

［1］SL74—95，水利水电工程钢闸门设计规范［S］.北京:中国水利水电出版社，1995.(SL74—95，Hydraulic and Hydroelectric Engineering Specification for Design of Steel Gate［S］.Beijing:China Water Power Press，1995.(in Chinese))

［2］水电站机电设计手册编写组.水电站机电设计手册［M］.北京:水利电力出版社，1986.(The Compilation Group.Manual of Mechanical Design of Hydropower Station［M］.Beijing:China Water Power Press，1986.(in Chinese))

［3］SL319—2005，混凝土重力坝设计规范［S］.北京:中国水利水电出版社，2005.(SL319—2005，Concrete Gravity Dam Design Specification［S］.Beijing:China Water Power Press，2005.(in Chinese))

［4］程兴奇，刘福臣，李凌霄.水工建筑物波浪要素计算探讨［J］.长江科学院院报，2009，(7):21 －24.(CHENG Xing-qi，LIU Fu-chen， LI Ling-xiao.Discussion on Wave Factor Calculation of Hydraulic Structure［J］.Journal of Yangtze Scientific Research Institute，2009，(7):21－24.(in Chinese))

［5］苗兴皓，于翠松，王艳玲.水闸波浪要素计算的探讨［J］.山东大学学报(工学版)，2002，(4):369 －371.(MIAO Xing-hao，YU Cui-song，WANG Yan-ling.The Study for Wave Element of Sluices［J］.Journal of Shandong University，2002，(4):360－371.(in Chinese))

［6］张培忠.MathCAD学步随笔［M］.北京:中国水利水电出版社，2013.(ZHANG Pei-zhong.Learning of Math-CAD of Step by Step［M］.Beijing:China Water Power Press，2013.(in Chinese))

［7］同济大学.高等数学［M］.北京:中国高等教育出版社，1999.(Tongji University.Higher Mathematics［M］.Beijing:China Higher Education Press，1999.(in Chinese ))