一种新型的组合赋权方法及在水闸安全评价中的应用

闫 滨，孙友良，闫胜利，郭 超，刘桐渤

(1.沈阳农业大学 水利学院，沈阳 110866;2.辽宁水利职业学院，沈阳 110122;3.辽宁省朝阳县水利水保局，辽宁 朝阳 122000;4.辽宁省防汛抗旱指挥部，沈阳 110003;5.大连庄河市水务局，辽宁 庄河 116400)

在水闸安全评价中，指标权重具有举足轻重的地位，指标权重的精确度与合理程度直接影响水闸安全等级的判断。根据数据来源不同，权重的确定方法大致可分为3类:一类是主观赋权法，其数据主要由专家根据经验主观判断得到，如Delphi法、模糊二元比较法和层次分析法(Analytic Hierarchy Process，简称AHP)等;第二类为客观赋权法，其数据由各被评价单位的实测数据得到，如离差最大化法、均方差法和主成分分析法等;第三类为组合及交错式赋权法，其数据是以主、客观赋权法确定的权重值为基础，再按照一定的方法进行优化。目前水闸安全评价体系尚不规范，指标权重计算方法往往单一、粗略。为减小主观随意性，使对指标的赋权达到主观与客观的统一，本文提出一种新型组合赋权方法，并应用于水闸安全评价指标赋权中。

1 水闸安全评价研究现状

在水闸安全综合评价中，常用的指标赋权方法有:Delphi法、模糊二元比较法、AHP法和熵权法等。其中，Delphi法可以有效反映专家意见的离散程度，但是其专家调查表设计比较粗糙，评分结果多采用简单的累计相加，忽视了各专家评判尺度的差异，且随意性较大;模糊二元比较法采用两两比较后再排序的方式，克服了专家对指标的评分尺度存在差异的弊端，但是指标比较标准往往难以把握;AHP法的指标两两比较更能有效体现指标间的重要度差异，使权重计算结果更加合理，但是一致性校验不容易一次性满足，必须由专家反复调整比较值，工作程序比较繁琐，且具有一定的主观性;熵权法确定的指标权重更具客观性，但忽视了指标的重要度差异。由于指标权重确定方法各有利弊，若能采用组合赋权方式，选取主、客观多种赋权方法进行水闸安全评价指标权重计算，并加权融合，必将有效发挥各种赋权方法的优点，使评价结果更趋合理。

组合赋权法［1］和交互式赋权法在其他领域已有应用，但水闸安全评价领域尚未借鉴。近年来一些学者将主、客观2种权重以相乘的方式融合，但这种办法不但没能体现主、客观赋权法的优越性，反而放大了权重间的差异，导致部分指标权重被过分放大或缩小甚至失真。国内外对于水闸安全评价的权重问题还鲜有研究，徐兴中等［2］、朱琳等［3］提出一种基于群决策和变权法的水闸老化模糊综合评判法，强调了资料信息对权重的作用;何鲜锋［4］提出了变权模糊综合评估和基于人工神经网络评估的方法，对水闸各指标的安全评分做了网络训练，并用变权法计算其指标权重，使评价指标的评分和权重排除了一定的主观因素干扰;曹邱林等［5］分析了水闸健康综合诊断权重确定方法，在改进AHP法基础上，根据分权重相差欲小欲优的准则，提出基于最优化准则的权重系数融合方法，避免了单一方法的缺点;何艳霞［6］将物元分析法应用于水闸评价，结合专家打分确定权重系数;田丰［7］引入区间AHP，在构造判断矩阵时，用一个区间数来反映事物的状态，在很大程度上反映了水闸的模糊性，并将区间AHP与熵权法确定的权重相乘，得到了综合主、客观优点的权重;孔楠楠［8］利用模糊相对隶属度矩阵确定指标权重，有效反映了指标的重要度;宋小波等［9］以专家打分法和熵值法作积的方式确定水闸安全评价指标权重，融合了专家经验和客观信息。

2 新型的组合赋权法

本文提出的组合赋权法是以三标度层次分析法和改进离差最大化法为基础，分别代表主、客观赋权方式。考虑到传统九标度层次分析法的缺陷，引入三标度层次分析法作为主观权重计算法;鉴于水闸破坏程度的判断是一种模糊问题，水闸安全类别的判定适合采用聚类分析，因此，引入白化权函数将有助于有效把握水闸各指标的安全类别倾向，并将传统白化权函数加以改进，将各指标的白化权函数值作离差，根据离差最大化法原理计算指标权重。

2.1 三标度层次分析法

AHP法能够合理地将定性与定量的决策结合起来，按照思维和心理的规律把决策过程层次化、数量化，通过建立有序层次、两两比较、建立判断矩阵以及计算特征向量等步骤计算权重。虽然AHP是对定性问题进行定量分析的一种简便、灵活而又实用的多准则决策方法，但是传统AHP法仍存在一定的缺点，如:标度分级较多，指标比较时很难掌握尺度，易造成判断矩阵的不一致;一致性检验不符合要求时，需要专家重新按照标度比较，较为繁琐;一致性比率C.R(Consistency Ratio)＜0.10，缺乏科学依据。为此本文引入三标度层次分析法［10］，计算步骤如下:

(1)建立比较标度矩阵。

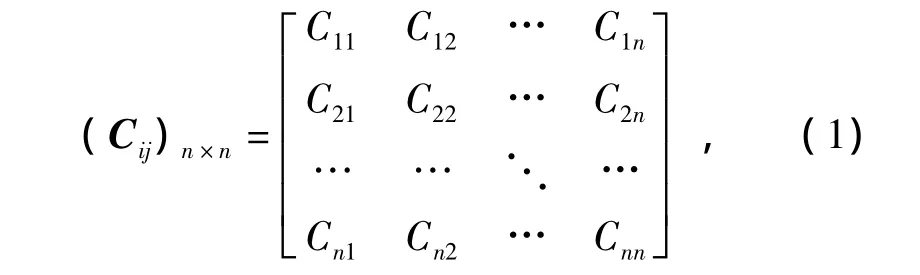
式中:

i，j为指标序号。

(2)计算最优传递矩阵。

(3)将矩阵O转化为一致性矩阵D，即为判断矩阵。

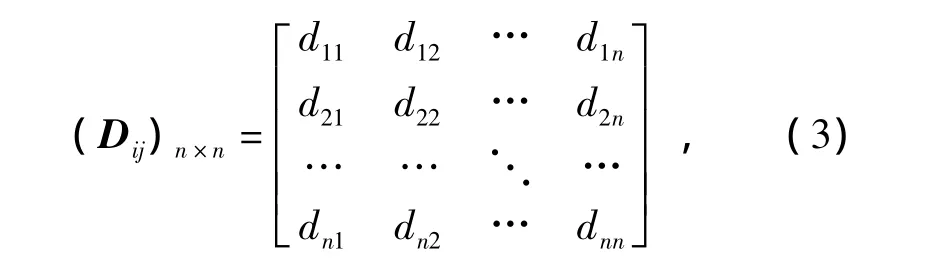
式中dij=exp{Oij}。

(4)计算判断矩阵的特征向量λi，并进行归一化处理，ηi即各指标权重，i=1，2，…，n。

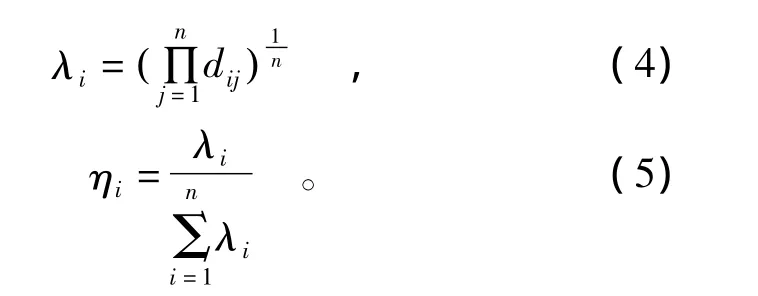
综上，三标度法在判断矩阵的建立上，不需要界定指标间的相互重要程度是多少，其原理是对指标重要性进行排序，从而避免了传统AHP法在指标互相比较时难以把握的情况，减少了人为误判;通过最优传递矩阵使判断矩阵具有一致性，省去了传统AHP法一致性检验的步骤，提高了计算效率，同时规避了一致性检验标准缺乏根据的问题。

但是，当指标数较少时，三标度法只能机械地排出指标的重要度顺序，不能描述各指标的相对重要程度，例如，2组指标的重要程度分别为:C1=0.1，C2=0.2，C3=0.7;C1'=0.1，C2'=0.4，C3'=0.5。2 组指标重要度不同，但重要度排序相同，经过三标度法计算出来的权重都是:0.148，0.289，0.563，这显然是失真的。虽然传统AHP法在两两比较时容易出现不一致的现象，但是当指标数较少时不容易出错，而且能够灵敏地反映各指标的相对重要程度。因此，如能将2种方法结合使用将达到良好效果。

2.2 离差最大化法

离差最大化法［11］是使指标信息值总离差最大来确定权重，该方法可以有效地传递评价指标的数据信息和差别，根据系统自身状态确定权重，是一种客观赋权方法，能够体现数据的可信度，使可信的数据占有较大权重，适合与主观赋权法联合使用，使评价指标权重更为合理。本文提出的离差最大化法是一种基于改进白化权函数的权重计算方法，以改进白化权函数的函数值为离差计算的数据基础。

2.2.1 改进的白化权函数

白化权函数的作用是将各指标的评分值转化为各个等级的偏好倾向值，实现隶属度量化。本文分别采用传统白化权函数的上类和末类函数作为改进白化权函数的上类和末类函数，采用中心三角白化权函数［12］作为中类函数。

改进的白化权函数克服了传统白化权函数的缺点，不存在多重交叉现象，尤其是当某个指标值确定从属于某一类时，绝不可能还有从属于其它类的可能;指标值处于两相邻类别中间时，隶属于这2类的可能性分别是50%，符合人的基本判断思维;某一点指标对于各个灰类的隶属度之和等于1，使得隶属概率互补，较传统的白化权函数更合理。

2.2.2 离差最大化法原理

设系统分为s个类别，且有n个指标，令指标非归一化权重向量为

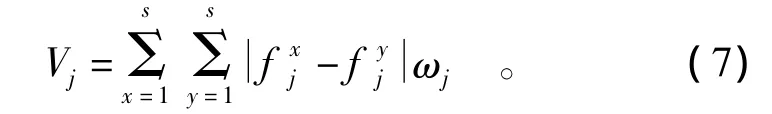
式中，x，y 均为 1，2，…，s;j=1，2，...，n。

令n维向量D为

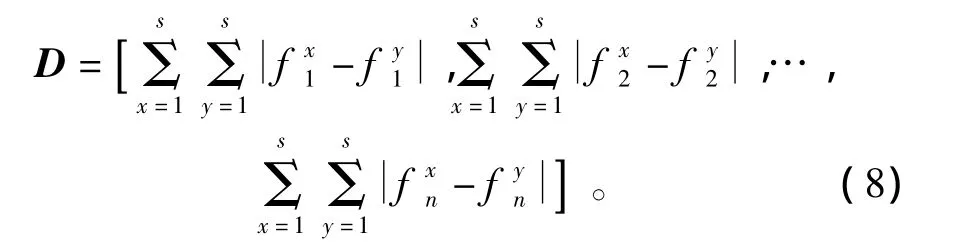
于是，得到基于改进白化权函数值的离差最大化法的灰色聚类指标权重系数求解模型:

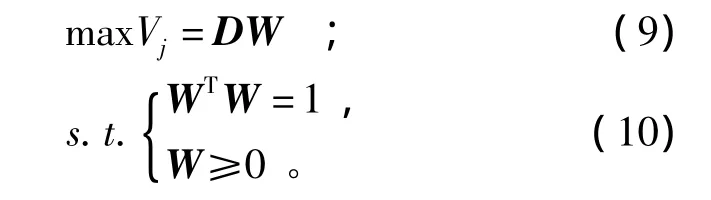
求解得:

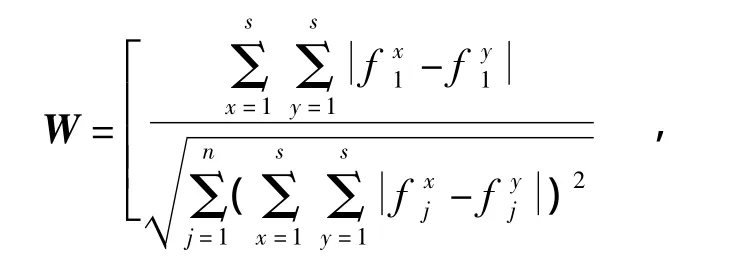
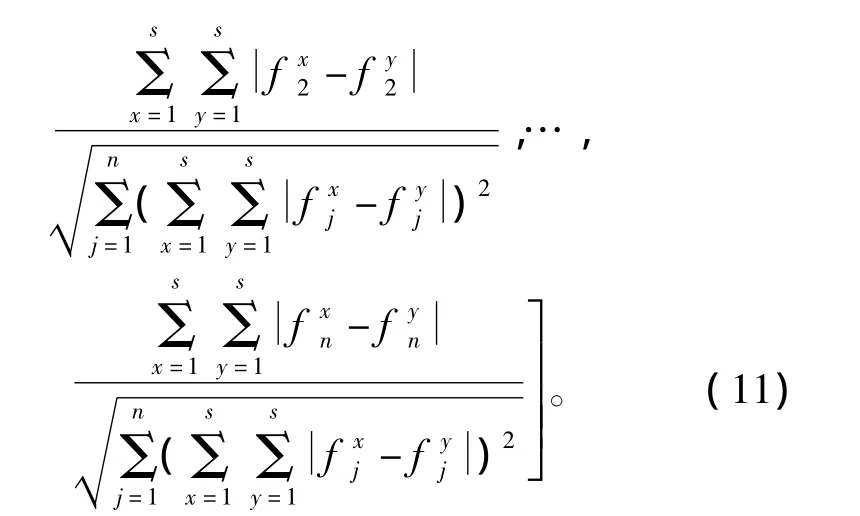
经归一化处理即得指标权重系数为

式中 j=1，2，...，n。

2.3 组合赋权法

为使指标权重计算结果更科学，可以采用组合赋权［13－14］方式，以使评价结果既能体现主观信息，又能体现客观信息。其中，主观赋权和客观赋权各有若干种赋权方法。设系统有n个指标，l种赋权方法所确定的权重向量组为 W=(W1，W2，...，Wl)，其中 Wk=(ω1，ω2，...，ωn)为第 k 种赋权方式的权重向量，k=1，2，…，l，n 为指标个数。令向量

式中，θ1，θ2，...，θl，为组合权重的线性分配系数，且满足单位化约束条件组合权重向量为

为消除不同量纲带来的不可公度性，应先将指标作无量纲相对化处理。一般地，指标可分为效益型和成本型。效益型是指属性值愈大愈好的指标，成本型是指属性值愈小愈好的指标。属性类型不同，无量纲化处理方法也有所不同。定义bj为指标的相对属性值。

在统计学中，离差是反映差异程度的一个重要指标。如果第j个指标的相对属性值bj对所有指标的相对属性值而言均无差别，则bj对重要性的排序将不起作用，这样的指标可令其权系数为0;反之，如果bj对所有指标的相对属性值有较大差异，bj对重要性排序将起较大作用，此时应该赋予第j个指标较大的权系数。基于上述原理，确定组合赋权系数向量Wc的基本思想是使所有n个指标的相对属性值对于其他指标的总离差达到最大，即达到最大，x，y=1，2，…，n 。

令n维向量B为

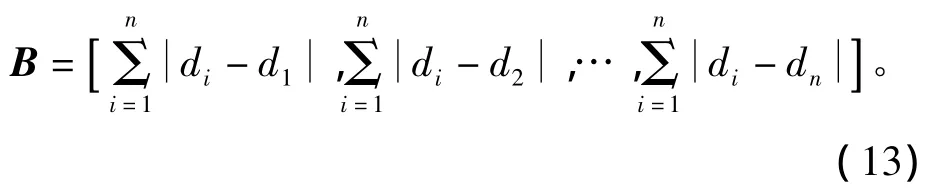
得到基于离差最大化法的组合赋权分配系数求解模型:

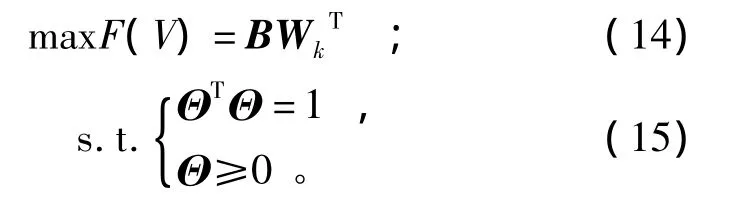
求解得组合权重线性分配系数为

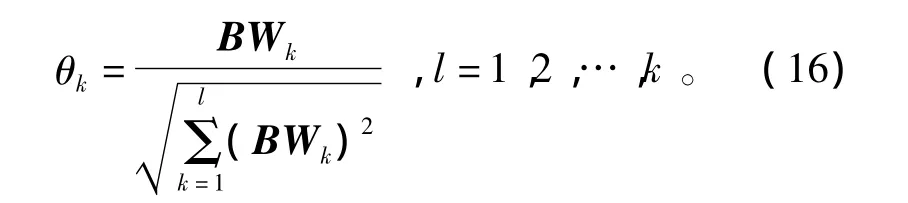
由于传统的加权向量一般都是满足归一化约束条件，因此为了与习惯用法保持一致，还需对其进行归一化处理。此时只需对θk进行归一化处理

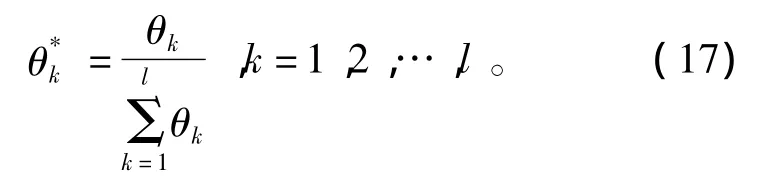
例如，某指标体系主、客观指标权重向量分别为:

W1=(0.5，0.2，0.2，0.1);

W2=(0.6，0.25，0.1，0.05)。

如果采用将2种权重相乘融合的方法，则综合权重向量为

Wc=W1·WT2=(0.8，0.133，0.053，0.013)，第一个指标的综合权重高达0.8，分别大于2种方法单独赋权时的指标权重，可见权重相乘放大了各指标的权重差异，这显然是失真的。如果采用本文提出的组合赋权法，将W1和W2加权融合则不会出现这种现象。不妨设Θ*=(0.4，0.6)T，则组合权重向量为Wc=0.4W1+0.6W2=(0.56，0.23，0.14，0.07)。另外可以证明，不管Θ如何设定，组合权重向量Wc内的指标权重都不会被夸张地放大或缩小。

3 计算实例

某拦河闸存在结构破坏、淤积、渗漏、设备老化等严重影响安全运行的问题。经现状调查分析、现场安全检测和工程复核计算后，对水闸进行安全评价，确定其除险加固或是报废。以水闸工程的可靠性作为评价总目标，以安全性、适用性和耐久性作为子目标，每个子目标又细分成若干分指标，以此方式拟定水闸安全评价指标体系，如图1所示。根据SL214—98《水闸安全鉴定规定》，将水闸的安全类别分为4类，即一类、二类、三类和四类，分别表示水闸的破坏程度为正常、基本正常、异常和失常。以“电器设备”组为例，分层分组依次计算三标度层次分析法权重、离差最大化法权重和组合赋权分配系数。

(1)通过建立指标评分准则，得到各指标评分dj。

令Dj=［变压器，继电器，闸门控制系统，供配电系统，电动机，其他电器设备］=［d1，d2，d3，d4，d5，d6］=［0.7，0.75，0.76，0.65，0.77，0.7］。

(2)三标度层次分析法权重。按照评价指标体系，通过专家打分，对比各指标的相对重要度，进而建立判断矩阵

采用三标度层次分析法计算主观权重结果为

(3)离差最大化法权重。建立改进白化权函数f1，f2，f3，f4，分别表达正常、基本正常、异常和失常，函数形式如图2所示。

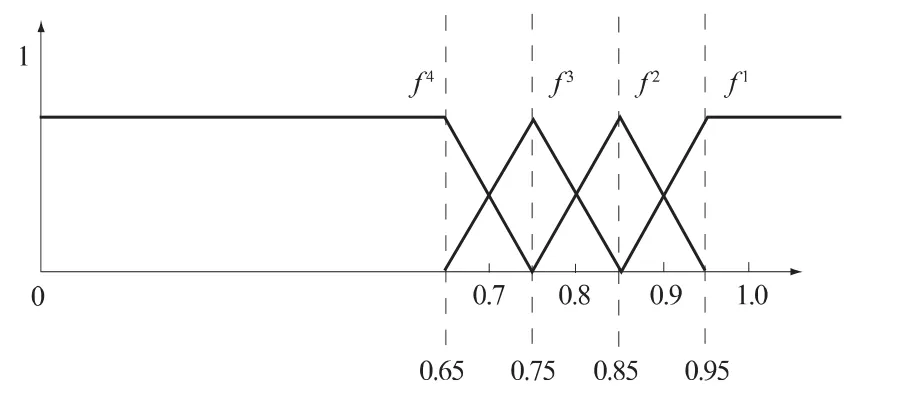
图2 改进白化权函数图Fig.2 Improved whitenization weight function

将dj代入4个函数中得白化权函数值矩阵X为

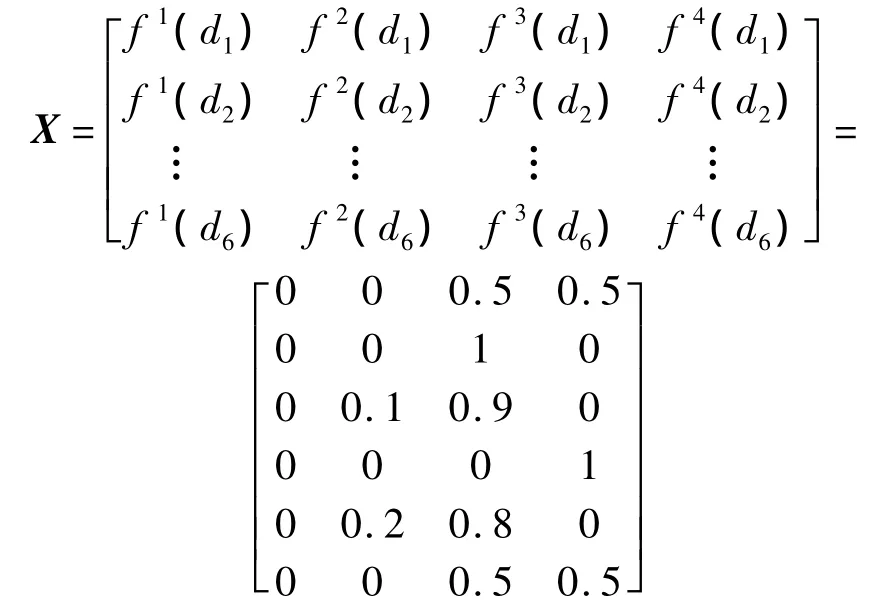
按照离差最大化法数学模型计算得客观权重W2=［η1'，η2'，η3'，η4'，η5'，η6'］=［0.130，0.195，0.182，0.195，0.169，0.130］。

(4)组合权重。组合权重的线性分配系数为

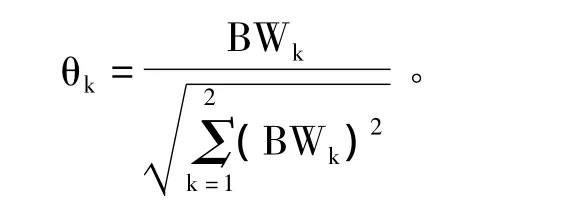
则组 合 权 重 Wc=(ωc1，ωc2，...，ωc6)=W1θ1*+ W2θ2*=(0.116，0.150，0.192，0.217，0.229，0.096)。

因此，“电器设备”组内各指标的组合权重分别为0.116，0.150，0.192，0.217，0.229，0.096，其中供配电系统和电动机在聚类分析评价中要占据较大权重。另外，三标度层次分析法体现了指标的重要度，离差最大化法体现指标信息值的模糊可信度。在该水闸电器设备评价指标体系中，闸门控制系统、供配电系统、电动机3项较为重要，需要占有较大权重;继电器、闸门控制系统、供配电系统、电动机4项指标具有比较明确的隶属等级，对该水闸的安全等级判断影响较大，应当占有较大权重;根据优化求解得到的线性分配系数，认为该水闸电器设备评价指标体系赋权所考虑的主观因素和客观因素的影响相差不大。

4 结论

(1)采用层次分析法建立判断矩阵时，三标度法简易，且更容易操作，克服传统AHP法在元素间作比较难的弊端;并且，三标度法建立的判断矩阵本身具有一致性，因此不需要进行一致性检验，克服传统AHP法需要经常调试、计算效率低的缺点;但三标度AHP法尚存在一定的问题，在指标较少的情况下，难以准确反映各指标的重要程度，甚至与事实相悖，尤其是指标个数少于4的情况。因而，指标个数少于4时宜采用传统AHP法，指标数较多时采用三标度法。

(2)本文提出的离差最大化法基于改进白化权函数确定权重，反映了各指标老化等级隶属度的灰性，即灰度越大，不确定性越大，权重越小，可以有效减小不确定因素对整体评价的影响;该方法注重对指标安全类别的判断，尤其适合于水闸的聚类安全评价;不足之处在于没有准确反映指标的重要程度。

(3)本文采用的组合赋权法综合了主、客观赋权法的优点，有效利用了专家经验和数据信息，减小了主观因素和不确定信息的干扰，使权重计算结果合理化，具有一定的可操作性。经实例证实，该方法应用于水闸安全评价中合理可行，并可以考虑其他赋权方法的相互优化组合。

［1］闫 滨，孙友良，高真伟.水闸安全综合评价研究综述［J］.水电能源科学，2013，31(2):171 －173.(YAN Bin，SUN You-liang，GAO Zhen-wei.Review of Study on Sluice Safety Comprehensive Evaluation［J］.Water Resources and Power，2013，31(2):171 － 173.(in Chinese))

［2］徐兴中，张龙天.基于群决策和变权赋权法在水闸老化模糊综合评判中的应用研究［J］.科技进步与对策，2009，26(21):148 － 152.(XU Xing-zhong，ZHANG Long-tian.Application of Group Weight Decision-making and Variable Weight to Fuzzy Integrated Evaluation on Sluice Aging Deterioration［J］.Science＆ Technology Progress and Policy，2009，26(21):148 －152.(in Chinese))

［3］朱 琳，王仁超，孙颖环，等.水闸老化评判中的群决策和变权赋权法［J］.水利水电技术，2005，36(4):98－101.(ZHU Lin，WANG Ren-chao，SUN Ying-huan，et al.Application of Group Weight Decision-making and Variable Weight to Synthetic Evaluation on Sluice Aging Deterioration［J］.Water Resources and Hydropower Engineering，2005，36(4):98 －101.(in Chinese))

［4］何鲜峰.水闸系统可靠性评价理论及其应用［D］.郑州:郑州大学，2005.(HE Xian-feng.The Reliability Evalua-tion Theory of Sluice System and Application［D］.Zhengzhou:Zhengzhou University，2005.(in Chinese))

［5］曹邱林，吴中如.水闸健康综合诊断的权重系数确定方法［J］.河海大学学报(自然科学版)，2008，36(5):646－649.(CAO Qiu-lin，WU Zhong-ru.Method for Determining Weight Coefficients of Sluice Health Comprehensive Diagnosis［J］.Journal of Hohai University(Natural Sciences)，2008，36(5):646－649.(in Chinese))

［6］何艳霞.山东黄河水闸安全评价方法研究［D］.济南:山东大学，2010.(HE Yan-xia.The Study of Sluices Safety Assessment Method of the Shandong Yellow River［D］.Jinan:Shandong University，2010.(in Chinese))

［7］田 丰.基于层次熵变权法的水闸模糊综合评价研究［D］.天津:天津大学，2008.(TIAN Feng.Study on Fuzzy Comprehensive Evaluation of Sluice Based on AHP，Entropy Endowing and Variable Weight Method［D］.Tianjin:Tianjin University，2008.(in Chinese))

［8］孔楠楠.多层次模糊识别理论在水闸安全评估中的应用［J］.水利与建筑工程学报，2012，10(3):71 －75.(KONG Nan-nan.Application of Multistage Fuzzy Diagnosis Theory in Safety Assessment for Sluice［J］.Journal of Water Resources and Architectural Engineering，2012，10(3):71－75.(in Chinese))

［9］宋小波，蔡 新，杨 杰.基于改进AHP法的水闸安全性模糊综合评价［J］.水电能源科学，2013，31(2):174－176.(SONG Xiao-bo，CAI Xin，YANG Jie.Fuzzy Comprehensive Evaluation of Sluice Safety Based on Improved AHP Method［J］.Water Resources and Power，2013，31(2):174－176.(in Chinese))

［10］马农乐，赵中极.基于层次分析法及其改进对确定权重系数的分析［J］.水利科技与经济，2006，12(11):732 －733.(MA Nong-le，ZHAO Zhong-ji.The Analyses of Calculating the Proportion Based on Analytic Hierarchy Process and the Improved AHP［J］.Water Conservancy Science and Technology and Economy，2006，12(11):732－733.(in Chinese))

［11］董一哲，党耀国.基于离差最大化法的灰色聚类方法［J］.系统工程理论与实践，2009，29(9):141 －146.(DONG Yi-zhe，DANG Yao-guo.Grey Clustering Method Based on Maximizing Deviations［J］.Systems Engineering:Theory ＆ Practice，2009，29(9):141 －146.(in Chinese))

［12］刘思峰，谢乃明.基于改进三角白化权函数的灰评估新方法［J］.系统工程学报，2011，26(2):244 －249.(LIU Si-feng，XIE Nai-ming.New Grey Evaluation Method Based on Reformative Triangular Whitenization Weight Function［J］.Journal of Systems Engineering，2011，26(2):244－249.(in Chinese))

［13］陈华友.多属性决策中基于离差最大化的组合赋权方法［J］.系统工程与电子技术，2004，26(2):194 －197.(CHEN Hua-you.CombinationDeterminingWeights Method for Multiple Attribute Decision Making Based on Maximizing Deviations［J］.Systems Engineering and E-lectronics，2004，26(2):194－197.(in Chinese))

［14］陈 伟，夏建华.综合主、客观权重信息的最优组合赋权方法［J］.数学的实践与认识，2007，37(1):17－21.(CHEN Wei，XIA Jian-hua.An Optimal Weights Combination Method Considering Both Subjective and Objective Weight Information［J］.Mathematics in Practice and Theory，2007，37(1):17 －21.(in Chinese))