基于LM的电阻抗成像的图像重建算法

陆鑫 （北京航空航天大学北海学院软件与信息工程学院，广西 北海536000）

电阻抗成像（Electrical impedance tomography，EIT）技术，是一项新兴的图像重建技术［1］。该技术要求在物体表面布上一层或者一圈电极，通过边缘注入电流时观察各个方向的电势情况，进行物体内部图像重建。与其他的医学成像方式比较而言，EIT技术具有成像的空间分辨率低但时间分辨率高的特点，可以在医学上用于肿瘤、骨伤、中风等伤情的监控［2］。

1 EIT问题的基本模型

EIT问题自70年代研究以来，已经提出许多图像重建算法［3－5］。

在磁场内部，由于生物组织磁导率低，所以磁场效应可以忽略不计，根据MaxWell方程及欧姆定律，可得出如下描述：

式中，ρ为电阻率分布函数；φ为电位分布；J为边界电流密度函数。由于生物组织内部无电流通过，故：

由式（2）可以得到生物内部电阻率与电位分布的关系：

该微分方程需满足的Dirichlet边界条件：

式中，Ω为物体所在的空间区域。

对于有电流注入的电极，Neumann边界条件为：

式（3）、（4）、（5）构成了EIT问题的基本模型［6］。

2 EIT问题的求解算法

2.1 LM反问题求解法

由问题（3）～（5）可知，求解电阻率分布函数ρ是一个非线性的反问题。由于非线性反问题的Tikhonov泛函不严格凸，且非线性算子不可微等，因此无法继续使用线性反问题使用的正则化方法。该问题可以用以下形式描述：

式中，F为ρ→V的非线性算子，并且ρ和V都属于Hilbert空间。

然而，在真正的EIT试验中，该方程往往是不适定的，测得的数据V往往带有扰动误差，笔者用δ表示，满足‖V－Vδ‖≤δ。为了找到解使得‖F（ρ＊）－Vδ‖，ρ∈Ρ取到最小值，笔者使用Levenberg－Marpuardt（LM）方法解决。

1）线性化。取其中的一个点的值为ρδk，在此基础上，将F（ρ）＝V线性化得到：

2）正则化。为了解决线性化后不适定的问题，笔者使用正则化。该问题可以描述成式（8）的形式，并且要解得其最小解：

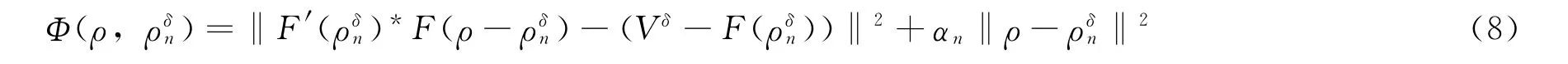
通过式（8）可以得到LM方法的迭代函数：

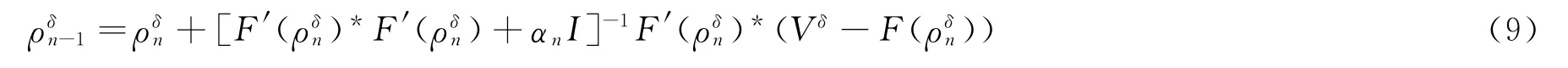
式中，αn是LM方法的调节因子。

2.2 负梯度算法

求解EIT电阻率分布函数问是一个多维无约束问题，可应用多维无约束优化方法。负梯度算法的过程如下：在初步测量时取出数据ρ（k），一维寻优解的方向为s，根据负梯度方向为－▽f（ρ（k））进行迭代：

用φ（ρ）来表示函数表达式（10）的目标函数，根据函数（12）的求导结果，可以计算出步长αk：

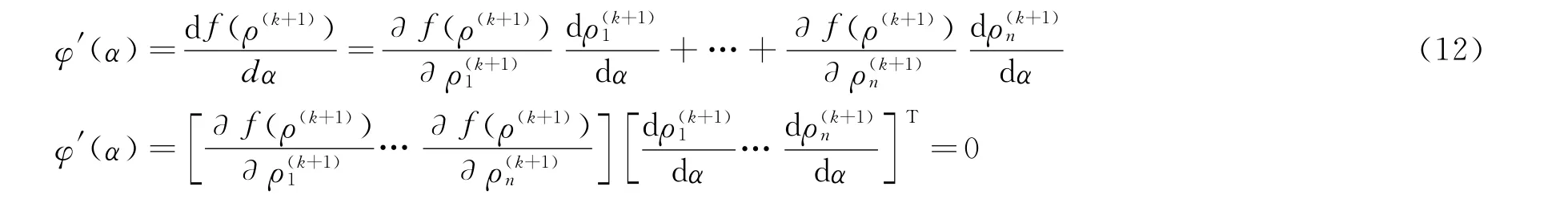
通过求极值点可以得到α的值，再将该值引入到下一轮寻优中。其收敛精度为：

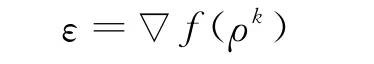
在实际构图的过程中，笔者发现原始的LM算法收敛速度较为稳定，虽然它与非线性最小二乘问题的高斯－牛顿算法都被认为是解决EIT问题的有效方法之一，但是实际的图像重建中效果并不理想。负梯度算法的收敛图像存在锯齿现象，虽然在开始的迭代中收敛速度很快，但是靠近极小值时收敛速度较慢。

3 基于负梯度法的LM算法

考虑到LM算法以及负梯度算法的各自优缺点，笔者采用负梯度算法与LM算法的联合算法。在EIT计算中前期可以用负梯度法迭代，提高收敛速度，后期使用LM算法，保证收敛的精准。对于负梯度算法，笔者给出一个收敛最小值ε用以控制迭代精度。

下面给出基于负梯度法的LM算法的具体流程：

1）取定ρ0，测得边缘电压V，边界电流分布J。设置负梯度算法迭代收敛最小值ε，LM算法结束阀值εlm，n为迭代次数。

2）取ρk初值为ρ0，设定初值αk。

3）根据式（11）、（12）计算ρk＋1。

4）令φ′（α）＝0，解得最优步长αk。

5）检验是否▽f（ρk）＞ε，若是转2）。

6）令ρn＝ρk，引入扰动算子后ρδn。

7）求解Φ（ρ，ρδn）的极小值，依据式（8）、（9）计算出ρδn－1。

8）检验是否αn＞εlm，若是转7）。

9）完整算法结束，得出最优解ρ。

4 Matlab试验及结果分析

在该网格建立的试验中，网格数量为2000个，节点数量为1000，如图1所示。在模拟的区域的中下方放置了一块圆形块状区域，用作模拟测试。图2为负梯度法的重建结果，图3为LM迭代算法的重建结果，图4为基于负梯度法的LM算法的图像重建结果。

图1 建立网格的图像

图2 基于负梯度法重建的图像

图3 基于LM迭代法重建的图像

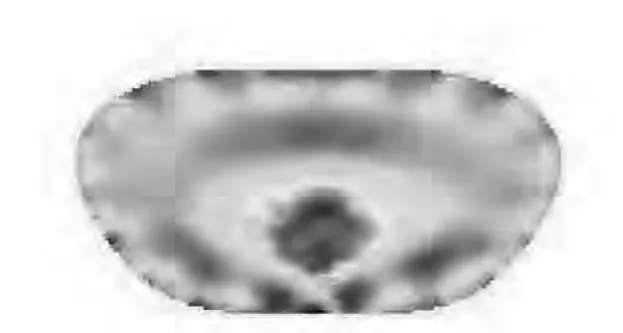
图4 基于负梯度法的LM迭代法重建的图像

图5 网格内放置物体的模拟图

与图5的原始放置物体的模拟图相比，显而易见，负梯度法图像失真最大，而基于负梯度法的LM算法最为靠近真实情况。

5 结语

研究并总结了负梯度法以及LM迭代算法，并提出了将负梯度法与LM迭代算法的结合算法。该结合算法具有一定的优化效果，改善求解问题的病态，但是在现实中应用电阻抗成像技术时仍存在许多难点与挑战，如图像分辨率不够高，重建过程时间长等问题。由于该技术还不够成熟，现有的条件还不可能让电阻抗成像技术能在临床医学上取代CT、MRI等传统技术。在该问题的进一步研究中，还需要国内外学者付出巨大的努力。

［1］ 董秀珍 .生物电阻抗成像研究的现状与挑战 ［J］.中国生物医学工程学报，2008，27（5）：641－646.

［2］ Bayford R.Bioimpedance tomography（Electrical impedance tomography） ［J］.Annual Review of Biomedical Engineering，2006，8：63－91.

［3］ Weberster J G.Electrical Impedance Tomography ［M］.Adam Hilger，Bristol and New York，1990：97－137.

［4］ Yorkey T J，Webster J G，Tompkins W J.Comparing reconstruction algorithm for electrical impedance tomography ［J］.IEEE Trans Biomed Eng，1987，34（11）：843－852.

［5］ Woo E J，Hua P，Webster J G，et al.A Robust image reconstruction algorithm for electrical impedance tomography ［J］.IEEE Trans Med Imaging，1993，12（2），137－146.

［6］ 杜岩，程吉宽，柳重堪 .用组合变尺度法求解电阻抗成像问题 ［J］.中国生物医学工程学报，1997（2）：18－20.