电力系统切换动态建模与励磁控制研究

李健勇，赵 峰 ，丁青青

(1.郑州轻工业学院计算机与通信工程学院，河南郑州450001;2.郑州大学 电气工程学院，河南 郑 州450001;3.清华大学电机工程与应用电子技术系，北京100084)

0 引言

区域电网互联发展和用电负荷增加使电网事故频频发生，互联电网大停电带来的巨大社会影响和经济损失迫使世界各国将电力系统安全提升到国家安全的高度.当电力系统的安全稳定运行条件遭到破坏而进入紧急状态或极端紧急状态时，需要采取紧急控制措施维持系统的稳定性［1-3］.

目前电力系统紧急控制研究主要集中在切机切负荷算法、混杂系统建模和稳定性分析等方面［4-6］.在基于反馈控制的电力系统紧急控制研究中，J.N.Peng等研究了切机操作与超导储能装置的协调控制问题［7］，文献［8］提出了高压直流输电设备的紧急支援控制策略.

励磁控制是提高电力系统暂态稳定性的重要手段［9-10］.由于 Hamilton函数方法能够充分利用系统内在的结构特点进行控制器设计，近年来在电力系统励磁控制研究中得到了成功应用［11-12］.注意到切换子系统的Hamilton函数在一定条件下能够构成多Lyapunov函数，Zhu等研究了切换耗散Hamilton系统在任意切换路径下的稳定问题，提出了两机电力系统的切换动态模型和稳定性［13-14］.

笔者研究IEEE三机互联电力系统在紧急状态下的切换系统建模和励磁控制问题，建立了电力系统的切换非线性系统模型，基于耗散Hamilton实现设计了切换控制器，证明了闭环系统的渐近稳定性.仿真结果验证了笔者所设计切换控制器的有效性.

1 电力系统切换动态模型

图1为IEEE三机互联电力系统.

图1 三机区域互联电力系统结构图Fig.1 Configuration of a three-machinemulti-area interconnected power system

假设在紧急情况下，系统中至少有1台发电机工作，则图1所示电力系统可能的工作状态有7种.

Ⅰ.切除1台发电机:(a)i=1，2;j=3;(b)i=1，3;j=2;(c)i=2，3;j=1.

Ⅱ.切除2台发电机:(e)i=1;j=2，3;(f)i=2;j=1，3;(g)i=3;j=1，2.

Ⅲ.3 台发电机同时工作:(h)i=1，2，3.

记 i∈ {1，2，3}为发电机编号，j∈ {0，1}表示发电机的运行状态，其中j=0表示电机被切除，j=1表示电机联网运行.

(1)发电机联网运行时，其动态可表示为

式中:δij为发电机功角;ωij为转子角速度;ω0为转子同步角速度;Pmi为机械功率;Peij为电磁功率;Mi为转动惯量;Di为阻尼系数;E'qij为x'di后电势;T'd0i为d轴开环暂态时间常数;xdi和x'di分别为d轴电抗和暂态电抗;Idij为d轴电流;Gii和Bii分别为第i台发电机节点电导和电纳;Bik为第i台和第k台发电机节点互电纳;Efdij为励磁电压.

(2)当发电机被切除时，其动态可以表示为

可以得到三机互联电力系统的切换非线性数学模型

式中:λ(t):［t0，+ ∞)→ Λ ={1，…，7}为切换路径.

2 耗散Hamilton实现

采用Hamilton函数方法对系统进行稳定性分析和控制器设计的关键步骤是完成受控系统的耗散实现.

定义1 考虑切换非线性系统(5)，如果存在连续可微函数Hλ(t)(x)使得系统为

式中:Jλ(t)(x)为反对称矩阵;Rλ(t)(x)为半正定矩阵，则系统(6)称为系统的耗散Hamilton实现，Hλ(t)(x)称为切换子系统的Hamilton函数.

为完成电力系统切换数学模型的耗散Hamilton实现，引入预置状态反馈控制［12］

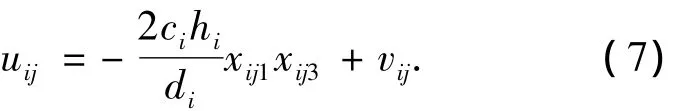
则在预置反馈控制(7)作用下，系统动态可以表示为

从而电力系统切换数学模型可以转化为

其中:Jλ(t)=diag{Jij(x)，Jij(x)，Jij(x)}，Rλ(t)=diag{Rij(x)，Rij(x)，Rij(x)}.

当j=1时，

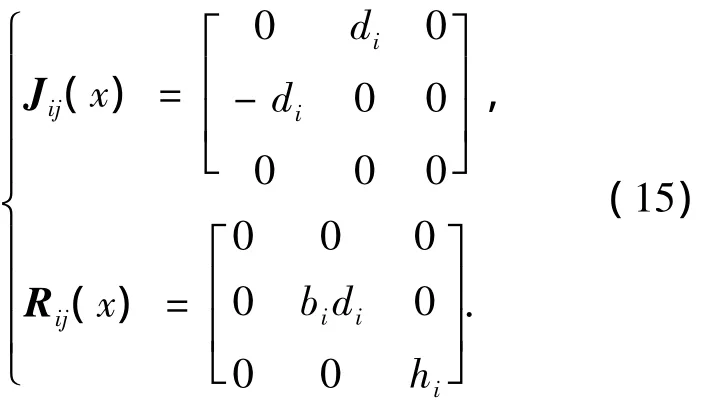
当j=0时，

显然 Jλ(t)为反对称矩阵，Rλ(t)为半正定矩阵，故(14)为系统的耗散Hamilton实现.

3 切换励磁控制器设计

基于电力系统切换数学模型的耗散Hamilton实现，可以利用各切换子系统的Hamilton函数构成多Lyapunov函数，并结合系统结构特性设计反馈控制器.具体地，选择切换控制器

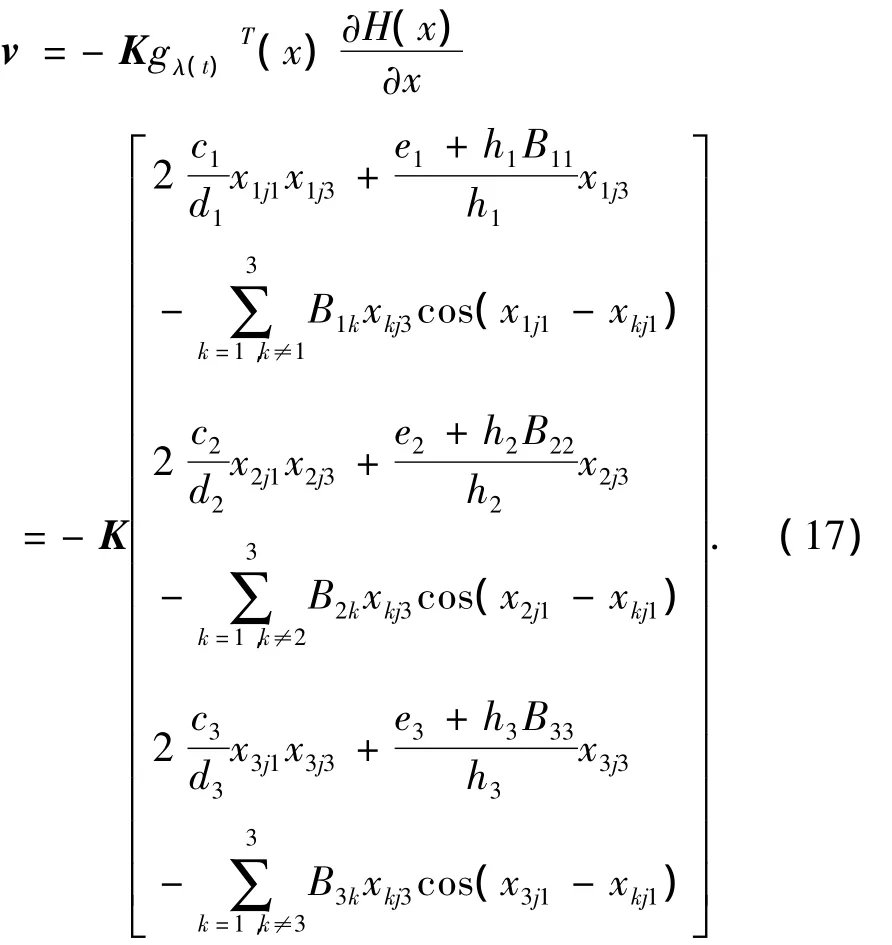
其中:j=1，K=diag{k1，k2，k3}＞ 0 为反馈增益矩阵.考虑到预置状态反馈(7)，原系统的励磁控制器为

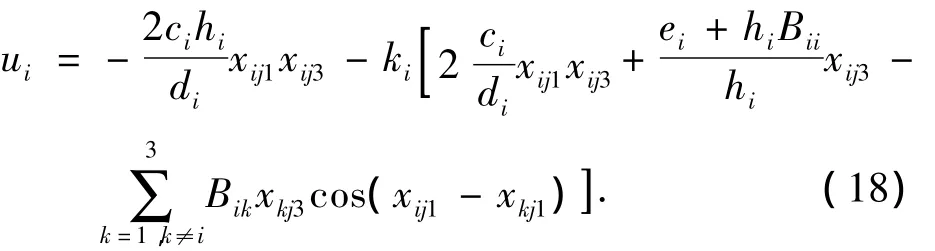
在上述反馈控制器作用下，闭环系统成为

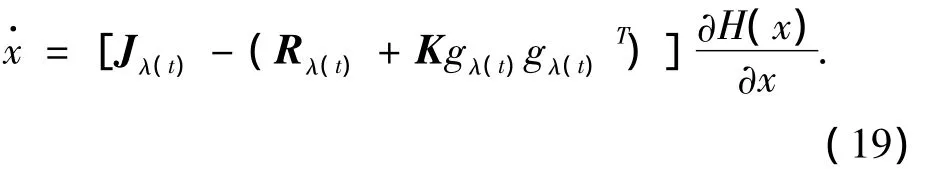
为分析闭环系统稳定性，首先对切换耗散Hamilton系统给出下面一般性结论［13］.

假设1 对切换耗散Hamilton系统(6)，如果∀i≠j∈Λ，∀x，y∈Rn，ΔHi=Hi(x)-Hi(y)和ΔHj=Hj(x)-Hj(y)具有相同符号，即sign(ΔHi)=sign(ΔHj)，所有的Hamilton函数具有相同的变化趋势.

引理1 对切换耗散Hamilton系统(6)，若假设1成立，则系统在任意切换路径λ(t)下稳定.若对∀i∈Λ，Ri(x)≥0，存在l∈Λ使得:①第l子系统关于零状态可检测;②对 任 意 正 数 c ＞ 0， 集 合=有限集，则系统(6)在任意切换路径下渐近稳定.

对电力系统，注意到在控制律(18)作用下，对所有子系统有

故所有子系统的Hamilton函数都具有相同的变化趋势，满足假设1，系统在任意切换路径下稳定.

下面以电机全部并网运行时的子系统为例分析系统的渐近稳定性.首先对该子系统，有

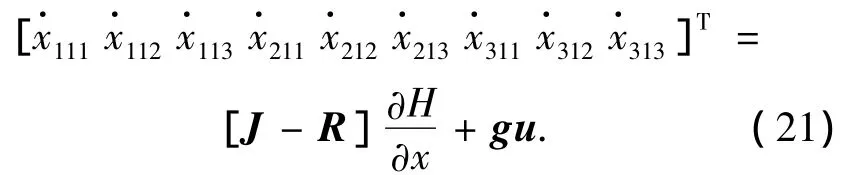
其中:J=diag{J11，J21，J31};R=diag{R11，R21，R31};g=diag{g11，g21，g31};u= ［u1，u2，u3］T.

令 xe=E'3qe)T为系统的平衡点，将系统状态作如下变量代换x=x'+xe.为简便起见，将x'仍记为x.

由式(22)和式(23)可得x≡xe，该子系统零状态可检测.进一步，对任意c＞0，式(22)和

的解集为有限集，故闭环系统渐近稳定.

4 仿真

为验证笔者所设计的切换控制器的有效性，在MATLAB/Simulink仿真平台上搭建IEEE三机系统进行仿真研究.发电机的容量分别为SM1=5 000 MVA，SM2=1 000 MVA，SM3=3 000 MVA.第5，7，8节点上的负荷容量分别为 S5=3 000 MVA，S7=2 900 MVA，S8=400 MVA. 发电机参数如表1所示.

表1 发电机参数Tab.1 Generator parameters

假设系统在t=0 s时联网运行，第3台电机由于故障在5 s时切除.仿真结果如图2和图3所示.

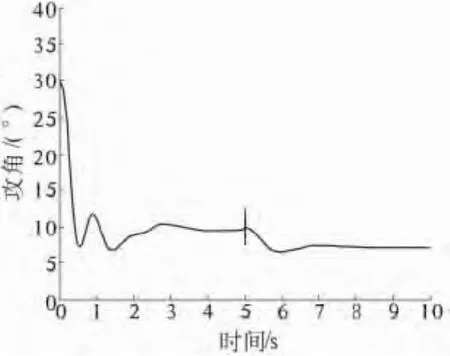
图2 切机前后功角响应曲线Fig.2 Response of the rotor angle

图3 切机前后母线电压响应曲线Fig.3 Responses of the bus voltages

从仿真结果可知，笔者所设计的控制器在电力系统发生切机操作时能有效提高系统的稳定性.

5 结论

研究了IEEE三机电力系统发生切机操作时的励磁控制问题.首先建立了系统的切换非线性系统控制数学模型，通过预置状态反馈完成了系统的耗散Hamilton实现，然后基于切换Hamilton系统理论设计了状态反馈切换励磁控制器，分析了闭环系统的稳定性.仿真结果表明笔者所设计的控制器能有效提高系统的暂态稳定性.笔者所提建模与控制器设计方法可以方便地推广到大型多机系统.

［1］ 薛禹胜.暂态稳定预防控制和紧急控制的协调［J］.电力系统自动化，2002，26(4):1-5.

［2］ DANIEL R V，PAVELLA M.A comprehensive approach to transient stability control［J］.IEEE Transactions on Power Systems，2003，18(4):1446-1460.

［3］ 林舜江，刘明波，周欣，等.暂态电压安全紧急切负荷控制优化研究［J］.电力系统保护与控制，2010，38(11):18-24.

［4］ ZHANG Xue-min，MEI Sheng-wei，WU Sheng-yu.Transient stability and emergency control［J］，Science in China，Series E:Technological Science，2009，52(2):420-428.

［5］ 刘凯，彭志炜，黄忠，等.基于混和逻辑动态模型的混杂电力系统及其电压稳定性分析方法研究［J］.继电器，2008，36(10):15-18.

［6］ YU Yi-xin，WANG Dong-tao.Dynamic security risk assessment and optimization of power transmission system［J］.Science in China，Series E:Technological Sciences，2008，51(6):713-723.

［7］ PENG JN，SUN Y Z，WANG H F.Co-ordinated emergency control of generator-tripping and SMES based on Hamiltonian system theory［J］.Electrical Power and Energy Systems，2005，27(5-6):352-360.

［8］ LI X Y.A nonlinear emergency control strategy for HVDC transmission systems［J］.Electric Power Systems Research，2003，67(3):153-159.

［9］ 卢强，梅生伟，孙元章.电力系统非线性控制［M］.北京:清华大学出版社，2008:4-20.

［10］刘宪林，杨建，王明东.励磁控制系统灰色预测PID控制仿真研究［J］.郑州大学学报:工学版，2006，27(2):70-72.

［11］刘艳红，宋伟华，王杰.包含SVC和非线性负荷的电力系统耗散实现与控制［J］，控制理论与应用，2010，27(1):47-52.

［12］WANG Y，CHENG D，LIC，et al.Dissipative Hamiltonian realization and energy-based L2disturbance attenuation control ofmulti-machine power systems［J］.IEEE Transaction on Automatic Control，2003，48(8):1428-1433.

［13］ ZHU Li-ying，WANG Yu-zhen.Study on the stability of switched dissipative Hamiltonian systems［J］.Science in China，Series F:Information Sciences，2006，49(5):578-591.

［14］ ZHU Li-ying，WANG Yu-zhen.On the modeling and stability analysis of switched two-machine power systems［C］.Proceedings of the 7th World Congress on Intelligent Control and Automation，2008，Chongqing，China:7192-7197.