复杂型腔环切拐角过渡刀轨生成技术
雷伟军,程筱胜,戴 宁,郭保苏
(南京航空航天大学 机电学院,江苏 南京 210016)
0 引言
在模具、医学修复体等各种表面形态复杂的零件中,型腔是一种常见的加工形状,常采用数控铣削的方式进行加工。对于型腔加工,生成合理的加工轨迹是保证加工质量和提高加工效率的一个重要途径。目前,常见的加工轨迹可分为线性走刀和非线性走刀。线性走刀主要包含单向行切和双向行切,单向行切在加工过程中存在大量的跳刀,其中50%以上的路径为非切削刀轨[1],加工效率低;双向行切虽然减少了来回跳刀的路径长度,但是在加工过程中采用往复的顺逆铣,降低了模型的加工质量和刀具寿命,不利于型腔的实际加工。在非线性走刀中,常见的有环切、螺旋线和摆线加工。螺旋线具有很好的光顺轨迹,加工过程平稳,适合高速铣削,但是螺旋线加工对加工轮廓形状有一定要求,最好是近似圆形和单连通的区域,并不适合复杂型腔的铣削加工。而摆线加工虽能保证刀轨G1阶连续,但是在加工过程中,刀具切削量少和刀轨路径过长,将影响整体的切削效率。环切加工由于加工轨迹连续,在加工过程中能够一直保持顺逆铣,切削效率和加工质量高,对解决复杂型腔的加工不失为一种很好的策略。但是,由于型腔轮廓本身形状和刀轨环在偏置中存在容易自交等因素,在生成的环切刀轨中普遍会产生一系列拐角,这些拐角在加工过程中会引起切削力大小和方向的突变,并带来机床频繁加减速等问题,若不能有效处理这些环切拐角,将影响整体加工质量和加工效率。为了在环切拐角处保证加工质量并实现平稳铣削,需要满足[2-3]:①切削力在切削过程中均匀变化,且低于刀具的最大许可切削力;②在拐角处的刀具轨迹要保持光顺连接,至少达到C1阶连续;③拐角处无残留量剩余;④加工过程中无多余空刀。若能在加工过程中满足这些要求,则将极大地提高型腔拐角的加工质量和加工效率,缩短整体加工时间,对型腔拐角加工具有很大的现实意义。
目前,对于环切拐角优化的研究主要集中在以下两个方面:
(1)从机床和运动学特性方面进行优化 张得礼[4]和何波[5]等考虑了机床的特性,为防止在拐角处发生过载,利用超前分析法和插入微小圆弧段的方法,提出多程序段的平滑算法,但是该方法难免会引起机床的频繁加减速,对数控系统的稳定性提出了较高的要求;PATELOUP 等[3]研究了拐角处进给速度和加速度的变化特性,通过修订拐角半径来增加实际铣削速度,并利用Bspline进行拐角过渡连接,能够达到在某些特定情况下的加速度连续,但是并没有考虑对环切残留量的去除问题。
(2)从刀具轨迹光顺方面进行优化 张鸣等[6]考虑环切拐角处产生的残留量问题,在原有环切刀轨上增加了清角加工轨迹,有效去除了拐角处产生的残留量,但是由于清角刀轨只能保证C0阶连续,在实际加工中会增加机床振动的频率,不利于实际加工;CHOY 等[7]采用弓状(bow-like)曲线进行拐角优化,其实质是对残留区域进行多次来回铣削,该方式无疑会增加拐角处的刀轨长度,并且需要大量的偏置操作来完成,从而导致效率低下;安鲁陵[1,8]和ZHAO[2]等采用单双圆弧方式进行拐角过渡连接,将直线和圆弧以及圆弧和圆弧连接的方式进行过渡连接,但是这种优化方式至多能达到刀轨的C1阶连续,不能保证加速度连续;WALTON 等[9]提出采用螺旋曲线连接的方式过渡拐角,根据角度不同分为C-shaped和S-shaped进行拐角插补,能有效地保证拐角的光滑过渡,但是没有考虑残留量对数控加工的影响。
由上述分析可知,目前对拐角刀轨优化的结果大多是达到过渡连接的C0~C1阶连续,只有少数文献能够实现在某些特定情况下的C2阶连续。在数控加工中,C0阶连续只能保证曲线在连接点的位置连续,不能确保速度和加速度的连续过渡,C1阶虽能保证曲线在连接点的速度连续变化,但其加速度在连接点处会产生突变,因此若在C0~C1阶连续的情况下进行拐角铣削加工,则因其加速度不连续,在实际加工过程中会引起机床的振动,而降低模型加工质量和加工效率。在加工过程中,C2阶连续不但保证了曲线过渡的速度连续,而且确保了其加速度的连续,从而大大减少由于机床频繁加减速带来的机床振动,能够有效提高型腔的加工质量和效率。
为了实现在环切拐角处的刀轨C2阶连续,本文在确保有效去除拐角残留量的情况下,提出采用三段式Clothoid曲线对拐角进行过渡连接,进而实现拐角的平稳铣削加工。首先采用基于骨架线提取的原理计算清角加工所需步长,然后在清角加工轨迹的基础上选取一系列点控制三段Clothoid曲线,从而实现拐角的光顺过渡,最后通过实例对比分析,证明该方法可以提高加工质量和效率。
1 拐角残区的识别与提取
在环切刀轨偏置过程中,若两线段的重叠率χ<50%,则会出现如图1所示的残留区域,其中Lpi和Lpo为外环进出线段,Lsi和Lso为内环进出线段。由于残留区域的存在,导致刀具在整个铣削过程中受力不均匀,影响刀具使用寿命,若残区存在于精加工过程中,则会影响最终的加工质量。对于残区的处理,以前常将残区作为一个单独的加工阶段进行加工,由于这些残区分布不均匀且零散,导致来回跳刀和下刀,影响加工效率。因此,这种方式已经逐渐被抛弃,而更加关注于如何在原有刀轨上增加切削刀轨来去除残区。

为有效切除这些残留区域,首先需要抽取残留区域的清角加工轨迹。传统的拐角残区计算方法是将尖角对之间的区域简化为一个直线相交的菱形处理[2],或者通过对拐角进行偏置和求交来计算残留区域。然而,这两种方法通过近似运算和大量求交运算后,结果的准确性和运算效率不容乐观。为了高效和准确地计算出残留区域所需的加工步长,本文借鉴骨架线提取[10-11]原理来计算残留区域的清角加工轨迹。
1.1 拐角骨架线与相伴曲线的映射关系
根据骨架线的定义,为便于描述,本文将拐角骨架线定义为从子环拐角到相邻外环对应拐角的所有相切于外环的最大圆盘的圆心集合,如图2中的子父环之间的虚线段所示。假设子环拐角进入段Lsi和输出段Lso之间的拐角点为p,则p称为拐角骨架线的起始点,Lpi和Lpo为拐角骨架线的相伴曲线。如图2所示,在p点和相伴曲线上垂足点q1和q2上建立对应的Frenet标 架,则相伴曲线与拐角骨架线上的Frenet标架具有如下映射关系:
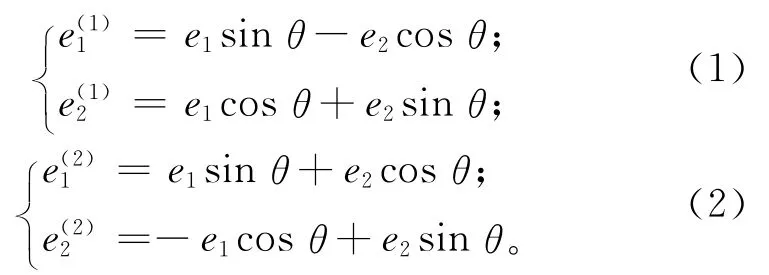
式中θ为e1和pq1的夹角。

由于相伴曲线Lpi和Lpo是到拐角骨架线距离相等的曲线,根据骨架线的对称性质,用r1和r2表述q1和q2的矢径,r表述p点的矢径,则Lpi和Lpo可以表述为

为建立拐角和相伴曲线的参数微分映射关系,对式(3)两端同时进行微分,用Frenet公式简化,可得

式中:k1和k2分别表示q1和q2在相伴曲线Lpi和Lpo上的曲率;s1,s2和s分别表示q1,q2和p处的自然参数。分别将与式(4)进行点乘,可得拐角骨架线和相伴曲线的参数映射关系式:

通过式(5)可以得到拐角骨架线的微分表达式,且可通过相伴曲线的曲率ρ1=1/k1,ρ2=1/k2得到拐角骨架线的曲率
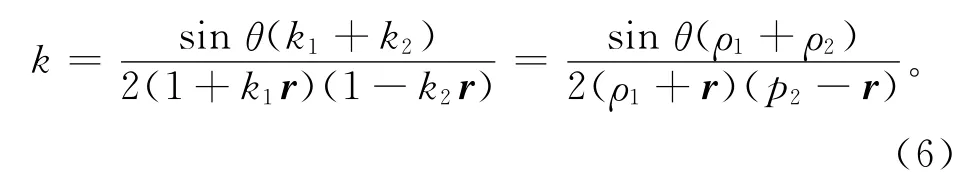
1.2 清角加工轨迹段的生成
根据泰勒公式,将高阶小量(大于等于三阶)省去,可得拐角骨架线的表达式为

式中:Δs表示沿e1方向的弧微分;p*表示骨架拐角线的一点;δ表示Δs所在圆对应的角度,δ=kΔs。
将1.1节中所求的相应参数代入式(7),能够求得下一点的位置,依次循环迭代,可以算出拐角骨架线上的所有点。然而,并不是所有的拐角骨架线都需要进行清角加工。事实上,当拐角骨架线所在的圆的半径r等于加工刀具的半径时,清角加工轨迹终止,所得的线段即清角所需加工步长,如图3b中的ppe段。
2 Clothoid曲线拐角过渡方法
若将1.2节中提取出的清角加工路径ppe直接添加到原有的刀轨中进行数控加工,则由于清角路径仅为一条延伸曲线,在加工过程中会进行来回折返运动,当加工至pe时,先降速为0然后迅速加速到降速前的速度,会引起机床的强烈振动,从而降低加工质量。因此,要想在拐角进行光滑过渡并保证较高的加工质量,应该在提取出的清角加工轨迹段的基础上进一步过渡优化,本文采用三段式Clothoid曲线进行拐角过渡连接优化。
2.1 Clothoid的定义与性质

Clothoid曲线常用于高速公路、桥梁的线形设计,以提高行车的速度和平稳性。最近几年,逐渐被应用于数控加工领域[9,11-12],生成螺旋刀轨和进行高速加工等。Clothoid曲线[13]是在Fresnel积分的基础上提出的,曲线的曲率变化与曲线的弧长呈正比关系,并且包含直线和圆的特殊情况。如图4所示,以弧长s为参变量,单位回旋曲线的表达式为:

将单位回旋曲线进行回转、比例和平移变换,可以得到回旋曲线的通用表达式:

式中:a表示比例因子,φ0 为直线在参考坐标系中的倾斜角。由该式可以推导出切线角φ、曲率k与弧长s之间的关系:

从式(11)可以得出,随着弧长的增大,曲线的曲率也随之增大。当s=0 时曲率k=0,即曲线在原点处时,曲线的曲率为零,这是Clothoid曲线的特性。利用这一特性连接Clothoid曲线和直线,能保证连接点的曲率连续,从而在连接拐角处的直线时能达到拐角的光滑过渡。

2.2 拐角过渡处理方法
获得了拐角残区步长线后,为了能够设计出光滑的曲线过渡,需要解决拐角的特征点、过渡范围以及曲线的连接顺序等问题,其拐角过渡曲线设计流程如图5所示。首先需要计算出拐角控制点来得到曲线过渡的范围,然后在控制点所构成的过渡区间内选择合适的初始插入点,最后以初始插入点作为直线和曲线的连接点,进行Clothoid 曲线过渡设计。
2.3 拐角过渡特征点的选取
拐角过渡特征点包括Clothoid曲线控制点和曲线初始插入点。为保证设计的Clothoid曲线不产生过切,需要在清角加工轨迹及父子环之间选取一系列点作为Clothoid曲线控制点(如图6)。由式(11)可知,曲线的曲率与弧长呈正比关系,与缩放因子呈反比关系,当弧长过大或缩放因子过小时都会严重影响曲线曲率的变化幅值。因此,在保证控制点处于父子环的尖角对之间的前提下,为了使曲线曲率的变化幅值均匀化,控制点所构成的多边形应尽可能对称,且所选的控制点便于Clothoid曲线连接。拐角控制点的选取步骤如下:

步骤1 做拐角p处两相邻线段(圆弧)Lsi,Lso的延长线(切线)Lsi_e,Lso_e。
步骤2 过pe点分别做Lsi_e,Lso_e的两条平行线,并与Lsi_e,Lso_e求交,记交点为pin_e,pout_e。
步骤3 若pin_e,pout_e在 父子环LsiLsoLpiLpo之间,则将pin_e,pout_e分别赋值给pin,pout;否则,计算延长线Lsi_e,Lso_e与父环Lpo,Lpi的交点,并将交点分别赋值给pin,pout。
步骤4 依次输出拐角p对应的三个控制顶点pin,pe,pout。
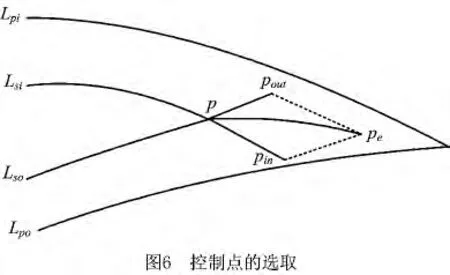
通过上述控制点的选取,保证了拐角残余线段ppe包含在控制点ppinpepout范围内,并且控制点没有超出父子环的区间。在控制点ppinpepout所构成的四边形范围内,刀具的实际切削路径为ppinpepout p,因此只需将四边形新派生出来的三个拐角∠pin,∠pe和∠pout进行合理过渡连接,就能完成对拐角∠LsipLso的光滑过渡。为实现过渡设计,首先需要选择Clothoid曲线的过渡初始点。
由于四边形四条边ppin,pinpe,pepout,poutp的长度并不完全相等,并且两条线段pinpe和pepout不能随意延长和改变,为了保证Clothoid曲线在拐角处的对称性,取pinpe和pepout中较短线段的中点作为其中一个插入点,将该点关于对应角的分线依次进行对称计算,得到相邻线段的插入点。如图7所示,由于pinpe的长度小于pepout,取pinpe的中点作为线段pinpe的过渡起始点pie,将pie对称到线段pepout上,得到pepout段的初始点peo,依次类推,可以得到pos,psi。
2.4 拐角过渡连接的设计
由于单位Clothoid曲线在原点的曲率为零,若将Clothoid曲线与直线进行合理连接,则会得到一条“直线-Clothoid曲线”光滑过渡的曲线,从直线到Clothoid曲线的曲率是连续变化的,保证了刀具在加工过程中的加速度连续变化。由于在2.3节特征点选取时考虑了过渡初始点的对称性,在用Clothoid曲线进行过渡连接时,应考虑曲线关于角分线的对称性,从而保证曲率的连续变化。

以图7中psipinpie段的拐角过渡连接为例进行拐角过渡连接设计说明,剩余两个拐角piepepeo与peopoutpos的过渡连接原理与此类似,不再赘述。图8a所示为psipinpie段的拐角过渡示意图,其中psi与pie为曲线过渡初始点,关于两直线的角分线对称,γ为两向量与的夹角。由于直线的曲率为0,要想光顺连接,必须使的两个端点psi,pie的曲率与两条连接线段的曲率相等,而Clothoid曲线只有在原点处的曲率为零,因此解决这一问题的办法是利用曲线关于角分线进行对偶。Clothoid曲线对偶是从psi与pie开始的回旋曲线的尾部按连续条件对接起来。由几何关系可知,两曲线在对接点处的切线角φm与两向量夹角γ的关系为

结合式(9),可以推导出对接点的最大参变数
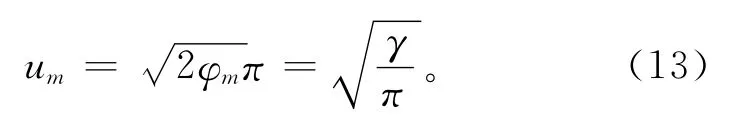
为了将对偶曲线合理地拼接起来,由式(9)可知,还需要求解对偶曲线的缩放因子a。由于psipin与pinpie的长度相等,且设为l,曲线通过缩放以后与长度l存在如式(14)的关系式,则缩放因子a可以通过式(9)与式(14)联立求解得到。缩放因子a的大小决定了Clothoid曲线的形态,图8b 所示为三段不同Clothoid曲线对应不同缩放因子的形态。

通过上述设计,能够很好地完成拐角的过渡,图8b所示为∠LsipLso的过渡连接示意图,经过渡后刀具的加工路径为其中:在直线过渡连接段ppsi和posp的曲率为0,在Clothoid曲线过渡段的曲率由0逐渐增大然后再缩小,保证了拐角过渡的曲率连续变化和刀具在加工过程中的平稳性。

3 实例及分析
本算法已经在仿真测试中得到了很好的应用,实验平台为配备有Core2E8400 3.00GHz处理器,2.00GB内存的Lenovo PC,开发环境为VC2008,并采用Hoops库进行刀轨显示和精雕V5.5刀轨仿真。
3.1 仿真测试实例
以不规则多边形和医学修复体加工为例,采用本文算法生成了环切刀轨的残区识别和拐角优化,用精雕V5.5 进行仿真,仿真机床参照德国imesicore340i机床的各参数进行了相关配置。其中,图9与图10分别表示不规则多边形不带岛屿和医学修复体带岛屿的拐角优化实例。图9a和图10a所示为传统的环切刀轨图,由图中可知,刀轨环进行等距的过程中产生了大量的环切拐角,不利于实际铣削加工。图9b和图10b所示为利用骨架线原理提取的拐角残区步长,虽然在加工过程中沿着该路径能很好地加工残留区域,但是在每个残区加工完成后都需要进行折返加工,这会严重影响加工的平稳性。图9c和图10c为加工残区Clothoid曲线过渡刀轨图,通过分析,采用Clothoid拐角过渡能很好地切除残留区域,并能保证加工过程的平稳性。图9d和图10d给出了采用本文方法优化后的刀轨仿真结果,从图中可见,运用该方法能很好地去除残留量。图9和图10两个仿真测试实例的参数和加工时间如表1所示。




表1给出了图9和图10中的两个仿真测试实例采用拐角未优化、三段圆弧过渡和本文算法的对比数据。由表1可见:①采用三段圆弧过渡的走刀路径长度最长,本文算法次之,没有优化的走刀最短。这是因为在具有相同控制点和初始插入点的情况下,Clothoid曲线的弧长小于圆弧的过渡弧长,因此Clothoid曲线的过渡走刀路径明显短于圆弧过渡路径。②采用Clothoid曲线过渡的测试加工时间明显短于三段圆弧过渡和未优化的加工时间,相比于圆弧过渡,Clothoid曲线能达到C2阶连续,因此在加工过程中能更好地提高切削速度,缩短加工时间。

表1 仿真测试加工主要参数对比
3.2 拐角过渡的曲率分析
为更好地说明拐角处Clothoid过渡的光顺性,以图9c中局部放大的图形为例分析过渡刀轨的曲率和运动变化规律。图9c中局部放大的拐角为36.4°,相邻环间的拐角残区步长为19.2 mm,两相邻控制顶点的长度为10.1mm,缩放因子a1=a3=10.736,a2=2.757。则在拐角处的过渡曲率如图11实线段所示,对应的虚线段为采用圆弧过渡的曲率变化,表2所示为本文算法对应的拐角过渡曲率变化值。在控制顶点内的过渡曲线是由三段Clothiod曲线光滑拼接起来的,曲率变化分为三段,分别对应图8中的进入段、拐角段和出去段的曲率变化。


表2 拐角过渡曲率变化值
分析图11和表2可知:①采用Clothoid曲线过渡能够保证过渡的曲率连续性,不会出现圆弧过渡曲率突变的情况,从而保证了过渡的C2阶连续。②拐角段的曲率比进出段的曲率变化幅值要大,这是因为在控制点构成的四边形中,中间段的角度变化幅值最大。③在实际加工过程中,机床运动的加速度与过渡曲线的曲率呈正比,相对于圆弧过渡,当采用Clothoid曲线过渡时,在角度幅值变化较小的情况下(进出段),能够自动增加曲率(加速度)变化的幅值,增加过渡的速度;而在角度幅值变化较大的情况下(拐角段,能够缩小曲率(加速度)变化的幅值,降低过渡的速度。这样,加工过程中在保证加工质量的同时,能够提高拐角过渡的速度,缩短加工时间。
4 结束语
本文针对复杂型腔拐角存在加工残留区域的问题,采用基于骨架线生成原理的方式进行拐角残区的识别及其步长的提取。该方法通过Frenet标架迭代的方式计算拐角骨架线,通过判断拐角骨架线到父环的距离,能够很好地计算出拐角残区的步长,避免过加工现象的发生。
本文针对环切中拐角所引起的机床振动和加工质量降低等问题,在拐角残区步长的基础上,提出采用三段Clothoid曲线光滑拼接的方式进行拐角过渡,这种过渡方式相对于圆弧等过渡方式,能够达到曲线的C2阶连续,并且能自动调节曲率变化幅值,提高加工效率。在实际加工过程中能够保证加速度的连续,从而保证加工过程中拐角的平稳过渡。
本文算法仍有不足之处,例如为保证最终的加工精度,对孤立和自交产生的刀轨环没有进行拐角过渡优化。事实上,在刀轨环自交分离出的子环仍可以进行拐角过渡,但是这种环的拐角过渡会对相邻环造成干涉等,具有更为复杂的情况,因此下一步的研究重点将是如何优化孤立的环和自交分离出的子环。
[1]AN Luling,ZHOU Laishui,WANG Yuguo,et al.Tool path generation for fine milling of pocket boundary corners[J].China Mechanical Engineering,2005,16(24):2188-2192(in Chi-nese).[安鲁陵,周来水,王玉国,等.型腔边界拐角精加工刀轨生成 算法的研究[J].中国机 械工程,2005,16(24):2188-2192.]
[2]ZHAO Z Y,WANG C Y,ZHOU H M,et al.Pocketing toolpath optimization for sharp corners[J].Journal of Materials Processing Technology,2007,192/193:175-180.
[3]PATELOUP V,DUC E,RAY P.Corner optimization for pocket machining[J].International Journal of Machine Tools&Manufacture,2004,44(12/13):1343-1353.
[4]ZHANG Deili,ZHOU Laishui.Adaptive algorithm for feedrate smoothing of high speed machining[J].Acta Aeronautica et Astronautica Sinica,2006,27(1):125-130(in Chinese).[张得礼,周来水.数控加工运动的平滑处理[J].航空学报,2006,27(1):125-130.]
[5]HE Bo,LUO Lei,HU Jun,et al.Smoothing algorithm for high speed machining at corner[J].Journal of Shanghai Jiaotong University,2008,42(1):83-86(in Chinese).[何 波,罗磊,胡 俊,等.高速数控加工轨迹拐角的速度平滑方法[J].上海交通大学学报,2008,42(1):83-86.]
[6]ZHANG Ming,LIU Weijun,LI Lun.Sharp corner clean-up CPO tool-path generating method for complex pocket[J].Computer Integrated Manufacturing Systems,2011,17(11):2399-2404(in Chinese).[张 鸣,刘伟军,李 论.复杂型腔环切清角加工刀轨生成方法[J].计算机集成制造系统,2011,17(11):2399-2404.]
[7]CHOY H S,CHAN K W.A corner-looping based tool path for pocket milling[J].Computer-Aided Design,2003,35(2):155-166.
[8]AN Luling,ZHOU Laishui,ZHUANG Haijun,et al.Tool path generation for high-speed milling of pockets[J].Journal of Computer-Aided Design &Computer Graphics,2004,16(9):1202-1206(in Chinese).[安鲁陵,周来水,庄海军,等.型腔高速铣削刀轨生成算法研究[J].计算机辅助设计与图形学学报,2004,16(9):1202-1206.]
[9]WALTON D J,MEEK D S.G1interpolation with a single cornu spiral segment[J].Journal of Computational and Applied Mathematics,2009,223(1):86-96.
[10]CAO L X,LIU J.Computation of medial axis and offset curves of curved boundaries in planar domain[J].Computer-Aided Design,2008,40(4):465-475.
[11]PAMALI A P.Using clothoidal spirals to generate smooth tool paths for high speed machining[D].Raleigh,N.C.,USA:North Carolina State University,2004.
[12]YAO Z Y.Path generation for high speed machining using spiral curves[J].Computer-Aided Design &Applications,2007,4(1-4):191-198.
[13]WALTON D J,MEEK D S.A controlled Clothoid Spline[J].Computers &Graphics,2005,29(3):353-363.
- 计算机集成制造系统的其它文章
- 基于模糊物理规划与互反馈的产品工艺方案绿色性分析
- 机械产品多质量要求下的选择装配方法

