机械产品多质量要求下的选择装配方法
任水平,刘检华,何永熹,蒋 科,郭崇颖
(北京理工大学 机械与车辆学院,北京 100081)
0 引言
选择装配(简称选配)是指通过检测和挑选待装配零件,有选择性地进行装配,以达到较高装配精度的一种装配方法。在一些精密机械产品(如航天器导引头)的生产过程中,由于其生产批量少且产品装配精度高,常采用选择装配技术来指导现场装配。选择装配中将需要保证的装配精度要求或装配功能要求称为质量要求,通常情况下装配体存在一个装配功能要求,称为单质量要求,例如在压气机部件的装配[1]中,需要保证的调整垫圈的尺寸公差即为单质量要求;而在一些高精度的装配体或由多个子装配体协同装配的装配体上,存在多个需要同时保证的装配功能要求,称为多质量要求。在一些复杂机械产品的精密仪器装调过程中,往往存在多质量要求的情况,且多个质量要求的重要程度不同,存在主次关系。在实际装调时,由于产品结构复杂,且主要质量要求的公差精度值较高或涉及到的公差项较多,装调难以达到满意的效果。
目前,国内外学者在选择装配技术方面取得了很多研究成果。Hag-Soo Kim[2]基于精密机械产品的装配特点,定义了1-匹配和d-匹配问题,提出一些利用数学规划和启发式算法进行求解的方法;哈尔滨工业大学邵锦文等[1]提出一个新的计算机辅助选配系统,采用并行组合的模拟退火优化方法求解零部件的匹配;吉林大学徐知行等[3]在蚁群算法的框架内提出一个考虑以信息素分布为节点模式的蚁群算法解构造图模型,并详细讨论了蚁群算法的实现过程。但是,以上研究成果仅考虑单一线性尺寸链,面向的是单质量要求下的选配问题。针对多质量要求下的选配问题,合肥工业大学刘明周等[4]通过构建复合选配目标,利用改进的混合算法实现了曲柄连杆机构中多对零部件的同时选配,但复合选配目标仅考虑匹配率,类似单质量要求下的选配问题。西北工业大学宋文龙、张栋、刘建东等[5-7]基于多装配尺寸链的选配模型,提出利用加权法、粒子群优化算法、多目标遗传算法来解决多目标选配问题,但未能充分考虑多个质量要求间的主次关系,在Pareto排序时未能考虑在产品装配精度不合格时首先满足主要的质量要求。
基于以上分析,笔者结合机械产品精密仪器的装调工程实践,基于产品多装配质量要求间的主次及耦合等关系展开选配技术研究,提出一种基于强弱Pareto和遗传算法的多质量要求下的选配方法。首先,根据复杂产品的多种装配质量要求建立面向三维空间的统一选配信息模型,并以装配精度和装配成功率为优化指标,建立多质量要求下的选配综合优化模型;然后,面向统一选配信息模型中的公差项实测值,采用一种以公差项为单元的编码方式,并在给定装配质量要求权重系数的基础上,基于强弱Pareto和密集度提出多目标排序的综合评价准则,进而在考虑关联约束排序的基础上,利用多目标遗传算法实现产品的选择装配,从而既保证复杂产品的多种装配质量要求,又达到在降低加工成本的情况下获得较高装配精度的目的。
1 多质量要求下的统一选配信息建模
因为由选择装配得到的产品可能具有多个需要同时保证的装配质量要求,且装配质量要求可能为一维尺寸公差要求,也可能为三维尺寸公差要求或形位公差要求,同时参与选择装配的零件尺寸或几何也可能存在相互耦合或关联的关系,所以建立合理有效的统一选配信息模型是进行选择装配的基础。
1.1 统一选配信息建模
目前,国内外常采用的选配方法是在零部件的批量加工样本中选择零部件实体,再依据由各公差计算得到的装配精度判断质量要求的优劣,但因为是先选择零部件,再依据各零部件上的公差实测值进行精度计算,最后依据装配质量的优劣进行组合优化,所以不能直接以装配精度为目标导向进行优化。因此,笔者依据复杂产品的多种装配质量要求,基于复杂产品的装配体模型建立装配精度计算模型,再结合公差项实测值等优化数据建立统一选配信息模型,然后直接对公差项实测数据进行组合优化,再选择对应的零部件样本进行装配,最终得到全局最优的装配方案。
根据上述分析,对整个选配过程进行数学抽象,建立以下统一选配信息模型:

式中:FR表示选配的质量要求,Masm表示选配的装配体,CMT表示选配的优化数据库,MF表示各质量要求对应的装配精度计算模型。整个统一选配信息模型如图1所示。

具体构成如下:
选配的质量要求FR代表了装配体要保证的多个质量要求,为三维空间中的尺寸公差要求或形位公差要求,一般用质量要求对应的装配精度表示,如果装配体的实际装配精度在规定范围内,则装配体是合格的,否则不合格。
装配体Masm记录了参与装配的子装配体及零件种类信息、零部件间的装配配合信息及位姿信息、零部件上的公差信息,由装配体信息及装配质量要求可以进行公差分析,得到装配质量要求对应的装配精度计算模型。
装配精度计算模型MF代表各公差项对各装配质量要求的影响,是选配方案优劣判断的基础,一般为装配尺寸链模型或基于SDT矢量的偏差网络图模型等,在数学上表现为偏差传递表达式。如在三维装配尺寸链中,其偏差传递表达式为

选配优化数据库CMT记录了所有参与选配的公差及实测值集合等数据,包括选配公差项集合信息CST和关联约束矩阵信息Tre,其中Tre表示各公差项的关联关系。由于在产品的选配分析中,属于同一零件实体的公差项的实测值在同一批零件样本上测量获得,这就要求在选配过程中该项同时被选择或者不被选择。关联约束矩阵Tre表示公差间的关联约束关系,

式中Tre(ij)表示第i个公差项和第j个公差项的关联关系,系数为0或1,系数为1时表示两公差项属于同一零件,否则为不属于。在复合选配中,如果同一类零件有k个实体参与装配,则这k个实体上的公差只在矩阵中表现出一个实体的公差间的关系。
选配公差项集合CST由参与选配的多个公差项ST构成,每个选配公差项数据又可表示为

式中:TD为公差参数信息,包含公差设计值、上下偏差值等信息;RF为公差坐标系信息,用以表征公差在三维空间内的位姿;T为公差作用矢量,由旋量参数[8]表示,T将公差变动作用以矢量形式在RF坐标系下量化表示,形式为T=[Dθ]T=[x,y,z,α,β,γ]T,其中,D=[x,y,z]T和θ=[α,β,γ]T分别为沿x,y和z三坐标轴的平移矢量和转动矢量;CMeas表示该公差在批量零件上测得的实测信息,包括每一个零件样本上测得的公差实测值及零件样本编号。
当选配只涉及三维空间内的尺寸公差时,其偏差传递方向一般为z向,无须利用旋量参数进行公差分析,只需进行传递系数求解即可;而当涉及形位公差的选配时,则需利用旋量参数进行公差综合分析。
1.2 基于装配精度计算模型的选配综合优化模型
机械产品多质量要求下的选配为多目标优化问题,笔者基于装配精度计算模型,建立了考虑装配精度和装配成功率的多质量要求下的选配综合优化模型。同时,从系统的角度出发,单质量要求可以看作数量为1的多质量要求,建立的优化模型也应能解决单质量要求下的选配优化问题,因此在给出单质量要求下的选配综合优化模型的基础上,提出多质量要求下的选配综合优化模型。
(1)单质量要求下的选配综合优化模型
本模型提出的依据是日本学者田口玄一博士关于产品的质量定义[9],面向公差的优化一般考虑加工成本和质量损失成本,而在选择装配中,由于加工成本已定,主要考虑质量损失成本。因为在一些高精密仪器的装调中,希望装配精度越高越好,所以本文以选配产品的装配精度偏离理想值的平均损失成本为优化函数,确保装配精度的稳定性和可靠性,其表示式如下:
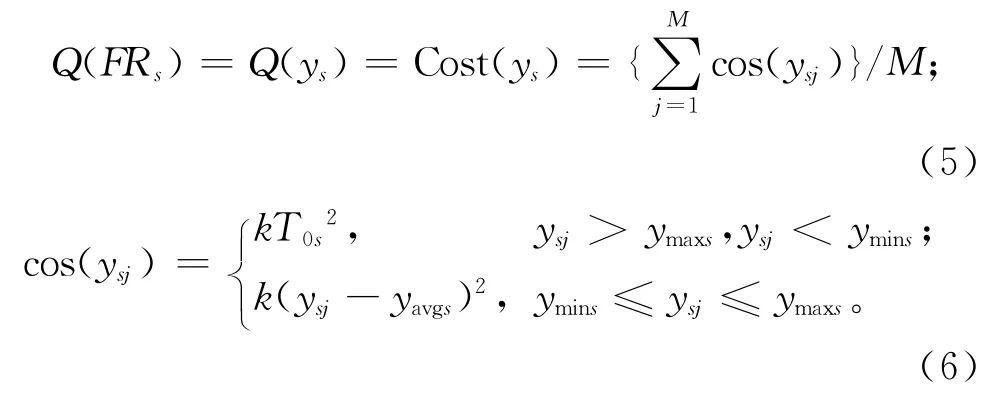
式中:M为一次选配得到的产品件数;ysj为第j件产品的第s个质量要求FRs的实际装配精度值,由1.2节中的装配精度计算模型MF带入实测值计算得到;ymins和ymaxs为FRs的设计最小值和最大值;T0s为FRs的设计公差 值;yavgs为FRs的设计中心值,yavgs=(ymaxs+ymins)/2;k为质量损失系数,当定义质量要求不合格,产品的质量损失阈值为A时,可得k=A/T02,在实例分析中,依据工程实际经验给出A值,则k成为固定常数,由计算公式可确定。
该方法考虑了如何提高匹配精度的问题,但在提高匹配率等方面还存在一些不足[3]。因为定义优化函数越小越优,所以结合装配成功率,提出综合质量Q(FRs)作为选配优化的目标函数:

式中:c(0≤c≤1)为常数,表示装配精度对装配质量的影响程度;η(FRs)为第s个质量要求FRs的装配不成功率;L为FRs符合要求的产品件数;φ是为了防止当c=0 且L=M时为使η≠0 而定义的基常数,可设φ=0.1。
由于定义优化方向为极小值方向,单质量要求FRs的选配综合优化模型可写为
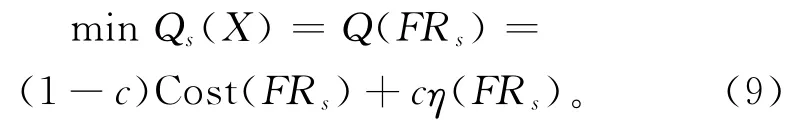
式中X为对实际零件样本的一次选配方案。
(2)多质量要求下的选配综合优化模型
基于单质量要求下的选配综合优化模型,可以建立多质量要求下的选配综合优化模型:
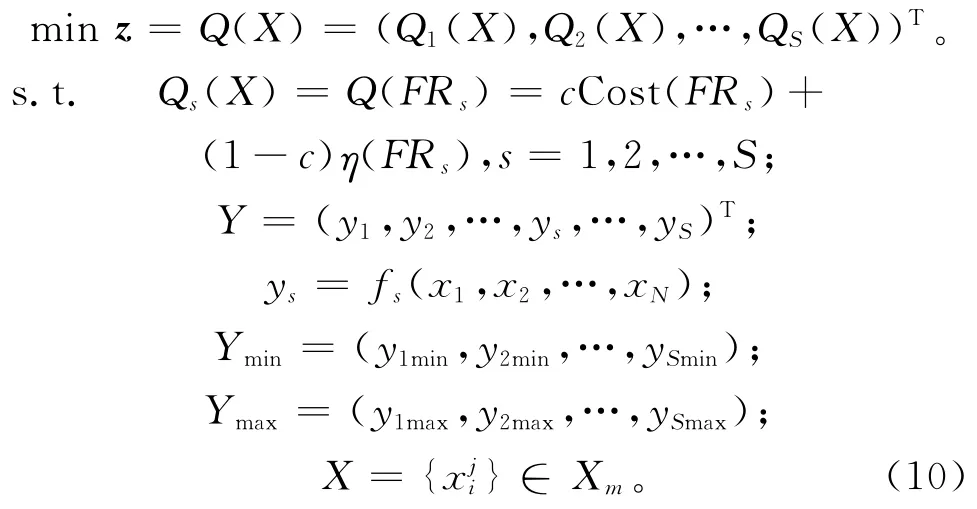
式中:z为目标向量;Y为多个质量要求;S为质量数;N为公差项数;fs为第s个质量要求对应的装配精度计算模型;Ymin和Ymax为各质量要求的合格边界为第i个公差项在对应的第j套零件样本上测得的公差实测值,X则由多个公差项的多个实测值组成,如2.1节所示,Xm为所有实测值集合得到的取值空间。
2 基于综合评价的多目标遗传算法
多目标优化问题(Multi-objective Optimization Problem,MOP)的经典求解方法是使用目标函数线性聚合或者基于Pareto方法[10]。线性聚合方法容易导致局部最优解,而基于Pareto的优化方法则能克服这些缺点,常用的有基于Pareto的遗传算法和多目标粒子群算法[11-12]。笔者依据第1章定义的统一选配信息模型,提出一种基于综合评价的多目标遗传算法来解决此类选配问题。
2.1 基于公差项的编码方式
由于选配问题是一类面向工程的实际问题,必须设计编码方式,将工程实际信息映射到优化数学过程中。在本文的选配分析中,由于直接对公差项实测数据进行优化,为避免不同公差项实测数据间的交叉引用,笔者对实测数据进行了分层表达,提出了一种基于公差项的矩阵编码方式X:

式中:矩阵的行数为,ki为公差项对应的这类零件在装配体中的实体数;表示第i个公差项在对应的第j套零件样本上测得的公差实测值;N和M分别为公差项数目和选配样本数目。装配时,从矩阵的每一行选取一个数据对应的零件,装配成一个装配体。
考虑到多目标遗传算子的设计,将编码格式设计为一维向量。同一公差项xi的多次实测值称为基因段Xi,每个基因段占据向量中的一段区域,则该向量中有N个基因段,其格式为

式中属于同一零件的各公差项的实测数据数量相等,且测量所属零件顺序在初始排列是一致的。
2.2 基于强弱Pareto和密集度的综合评价准则
多目标遗传算法的核心问题是多目标评价准则,笔者提出基于强弱Pareto和密集度的综合评价准则,并给出适应度函数来量化表示,以保障产品中带有主次关系的多个装配质量要求,并在质量要求不完全满足装配功能要求时,保障首先满足主要质量要求,从而实现多目标的优劣排序,得到最优解。
因为前文提到在S个质量要求间可能存在主次关系,需首先保证主要的质量要求,所以定义各质量的权重系数λs∈(0,1](s=1,2,…,S),通过强弱Pareto方式来体现主次关系。如果为主要的质量要求,则系数定为1;如果为次要的质量要求,则定义为小于1的常数,且次要质量要求系数仅表示一种关系,大小对结果影响不大。定义所有主、次质量要求的系数集合分别为Ωmajor={λs|λs=1},Ωminor={λs|λs≠1}。当Ωminor=∅,即所有要求的系数都定义为1时,所有质量要求间不存在主次关系,与基本的多目标选配情形相同。在这样的前提下,给出综合评价准则。
(1)强弱Pareto
可以采用支配解数全面表征强弱Pareto关系,为了引出代表个体在种群中优劣性的支配解数,本文先提出强弱支配关系的定义。
定义1 强支配关系。
设在多目标遗传算法优化时,个体种群为Pop,种群中的个体数目为P,个体标示为X,Qs(X)是个体每个质量要求的优化函数,如1.3 节所述。∀X(1),X(2)∈Pop,若Qs(X(1))≤Qs(X(2))(s=1,2,…,S),且∃l∈{1,2,…,S},使Ql(X(1))<Ql(X(2)),则称解X(1)强Pareto优于解X(2),或者称为X(1)强支配X(2),写作X(1)≺X(2)。强支配关系表示的是个体X(1)在各个方向上都优于个体X(2)。
定义2 弱支配关系。
当X(1)不能强支配X(2)且Ωminor≠∅时,若Qs(X(1))≤Qs(X(2)),{s|λs∈λmajor},且∃l∈{s|λs∈λmajor},使Ql(X(1))<Ql(X(2)),则称解X(1)弱Pareto优于解X(2),或者称为X(1)弱支配解X(2),写作X(1)≺minX(2)。弱支配关系表示的是个体X(1)在主要功能方向上优于个体X(2)。
由此定义个体X(u)在种群Pop中的支配解数Pa(X(u))|Pop,支配解数越大,表明该个体在种群中越优,其表达式为:


式中pa(X(u),X(i))为两个体间的支配关系系数。
(2)密集度
在大量粒子不存在任何支配关系时,利用密集度Den(X(u))|Pop进行排序。密集度描述了粒子在群体中与其他粒子的拥挤程度,可以用来表征种群的多样性,其表达式为:
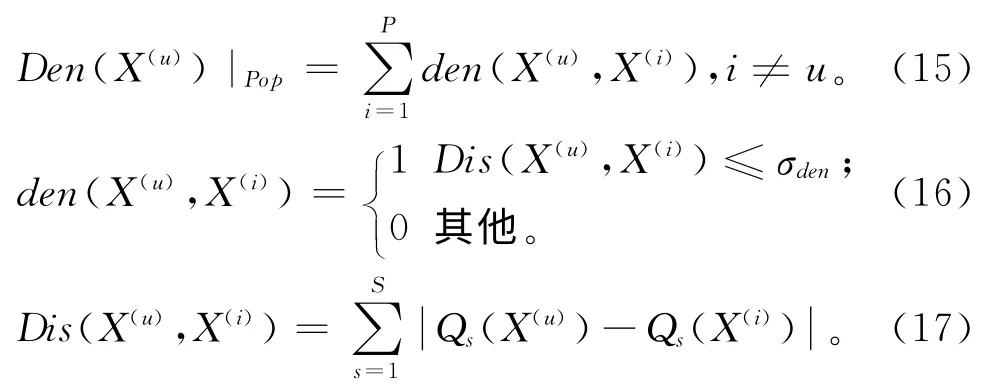
式中:Dis(X(u),X(i))表示两个体的拥挤距离,即两个体在各优化函数值上差值的绝对值的和;σden表示密集度参数,由实际问题定义。
(3)适应度函数
由表征加权Pareto关系的支配解数和密集度,可以给出表征综合评价准则的适应度函数Fit(X(u))|Pop,其表达式为

式中P为X(u)所在种群Pop的个体数目。利用适应度函数进行综合排序,一方面评价了个体的优劣性,保证主要功能要求得到满足;另一方面利用个体在种群中的密集度保证了种群能维持较高的多样性,使得搜索不陷入局部解。适应度将会是后续算法中快速排序的依据。
2.3 基于综合评价的算法流程
笔者提出的基于综合评价的多目标遗传算法是对传统多目标遗传算法的改进,其算法流程与传统多目标遗传算法的流程类似。在数据初始化后,通过遗传算子来推动优化过程持续不断地进行,并通过基于强弱Pareto和密集度的综合评价准则来进行优劣排序,最终基于停止准则输出最优解。由于本文的选配优化算法是直接对公差项实测数据进行组合优化,为了保证属于同一零件实体的不同公差项实测数据能同时被选中,笔者在优化过程中提出了“关联约束排序”这一概念,从而避免属于同一零件的数据被不同解集选中。
(1)遗传算子设计
在算法优化过程中,其核心过程是生成新种群和个体优劣排序,个体优劣排序由综合评价准则实现,新种群的生成由遗传算子实现。遗传算子包括选择算子、交叉算子和变异算子。
1)选择算子
选择算子用来选择参与交叉和变异的个体,本文采用轮盘赌方法[4]实现,根据个体适应度按比例来确定个体被选概率。
2)交叉算子
采用单点交叉对个体进行交叉运算。若随机数小于交叉概率Pc,则随机选配两个体进行交叉运算,选择随机数R(R=1,2,…,N)及R之后的基因段进行交叉。
3)变异算子
若生成随机数小于Pm,则对每个个体X的某一基因段Xi进行变异操作。在所有基因段变异完成后,个体X变异后成为X',然后对种群中其他个体进行变异。
(2)关联约束排序
在新种群生成过程中,需要对选择的个体进行交叉和变异操作,改变某些公差项实测数据的排列顺序,由于多个公差项可能属于同一零件,其多个实测值也由同一批零件测得,需要使这些实测值保持相同的零件编号顺序。为此,基于关联约束矩阵实现该排序,笔者将其定义为关联约束排序,以实现相关联公差项的同时组合优化,其流程图如图2所示。
(3)基于综合评价的多目标遗传算法流程
基于综合评价的多目标遗传算法,其数据结构由进化种群和外部优化集两部分组成。在算法运行时,第一步是进行数据初始化,要初始化的数据包括交叉概率、变异概率、所有质量要求的权重系数等变量参数以及进化种群、外部优化集等数据集合。在所有数据初始化完成后,再通过遗传算子推动优化过程持续不断地进行。依据选择算子在进化种群中获得被选择的个体,经过交叉和变异操作并满足关联约束排序,得到新种群,放入外部优化集中。利用加权Pareto和密集度得到适应度函数,依据适应度值进行快速排序,得到满足种群数大小的下一代优化种群和外部优化集,然后进行下一次迭代优化,在满足迭代停止条件后得到最优解。本文采用限定迭代次数为停止条件。基于综合评价的多目标遗传算法的整体流程如图3所示。


3 装配质量评定指标
在利用基于综合评价的多目标遗传算法进行多次选配后,可以获得多个优化方案。需要利用装配质量评定指标来比较方案间的优劣,由此给出产品装配成功率和产品装配精度这两个指标。
(1)产品装配成功率
若选配得到的一套产品满足所有质量要求,则称该产品是合格的。产品装配成功率

式中:M为一次选择装配得到的产品件数;SP为其中合格的产品件数。
(2)产品装配精度
产品装配精度评价模型δP用来评定装配产品的平均装配精度,

式中:S为质量要求数目;ysj为第j套装配产品的第s个质量要求的装配精度值;yavgs为装配体上第s个质量要求FRs的平均设计尺寸;T0s为FRs的设计公差值。
装配成功率反映了装配成功的数量,ηP越大,参与选配的零件越多,剩余零件越少,装配质量越高。装配精度则反映了装配精度的稳定性和可靠性,δP越大,装配精度越高。
4 实例分析
现以雷达装配中波导部件的选配实例来验证上述方法。波导部件由零件Pa、零件Pb和零件Pc装配而成,零件间靠工装定位,包括公差项T1,T2,T3和T4,装配结构示意图如图4所示。波导装配完成后,首先需要保证首尾两杆连接的端面之间的空间位置,其次需要保证在第一个工装处的空间位置,包括两个质量要求,其中质量要求2为主功能要求,质量要求1为次功能要求。
现在对从现场采集的20套产品的待装配零件进行选配分析,表1给出部分原始实测数据。在自主开发的计算机辅助选配系统中进行选配模拟实验,在虚拟环境中不考虑工装设备,构建波导的简化装配体模型,通过分析装配体结构并关联所有待装零件的实测值数据,构建统一选配信息模型,则可得各质量要求对应的装配精度计算模型,如表2所示,其中各公差项的关联约束矩阵



表1 部分原始实验数据

表2 公差设计参数及装配质量要求
在建立选配优化数学模型时,定义在当前实例中产品质量损失阈值A=100,则可由各功能要求的公差值求出质量损失系数。设定进化种群数P=60,外部优化集个体数Pout=10,最大进化代数Gen=60,交叉概率Pc=0.8,变异概率Pm=0.02。
首先依据各质量要求的主次关系定义质量要求权重系数,设功能要求1的权重系数λ1=0.05,功能要求2的权重系数λ2=1。设定优化原则为装配成功率优先,在优化模型中选取装配精度对装配质量的影响系数c=0.3。通过计算机辅助选配系统进行选配分析,如图5 所示,其中得到的一组Pareto结果,定义为解1,如表3所示。
在相同的原始数据下,应用随机组合的方法进行选配分析。应用装配质量评价指标,比较使用基于强弱Pareto和遗传算法的选择装配方法和随机选配两种方法所得到的结果,如表4 所示。从表4可以看出,在随机装配时,装配成功率得不到保证。而本文所提方法能显著提高装配成功率,得到精度要求较高的装配产品。
当不考虑各质量要求的主次关系时,定义λ1=1,λ2=1,其他参数不变,此时强弱Pareto支配关系失去作用,进行多目标选配分析,获得一组Pareto结果,定义为解2,将两种权重系数下的选配结果进行对比,如表5所示。


表3 基于强弱Pareto和遗传算法的选择装配Pareto解

表4 不同方法的装配质量评定指标对比

表5 不同参数下的选择装配结果对比
从结果可以看出,两个装配方案具有相同的产品装配成功率,并且解2合格产品的装配精度比解1要稍高。但是在工程实际中,当试装不合格时需要对不合格产品进行装调,而质量要求2为主要要求,可能存在精度要求高、装调难以达到要求的情况。而解1采用了强弱Pareto关系进行组合优化,在产品不能全部试装合格的情况下,能首先保证主要质量要求,提高质量要求2的装配精度,降低后续装调工作的难度。因此从整体上来看,解1 比解2更优,解1的产品质量更高。
5 结束语
本文分析了三维空间中多质量要求下的选配问题,构建了多质量要求下的统一选配信息模型,并基于该模型提出一种基于强弱Pareto和遗传算法的多质量要求下的选配方法。通过实例分析证明了该方法的可行性,该方法可有效地对三维空间中具有多质量要求的产品进行快速选配,保障产品中带有主次关系的多个质量要求,并能在质量要求不完全满足装配功能要求的情况下,保证首先满足主要质量要求,降低后续装调工作的难度,从而得到全局最优装配方案,提高装配成功率和装配精度。下一阶段工作是考虑面向形位公差的选配分析,在建立形位公差实测值的有效表征形式后,依据装配质量要求建立面向形位公差实测值的装配精度计算模型,在统一选配信息模型的基础上进行以形位公差为质量要求的选择装配。
[1]SHAO Jinwen,ZHANG Zhenjia,MA Yulin,et al.Applica-tion of parallel recombination simulated annealing algorithm in computer aided selective assembly system[J].Journal of Machine Design,2002(11):39-41(in Chinese).[邵锦文,张振家,马玉林,等.并行组合模拟退火算法在计算机辅助选配系统的应用[J].机械设计,2002(11):39-41.]
[2]KIM H S.Analysis of selective assembly operations in manufacturing[D].Ann Arbor,Mich.,USA:MI Company,1994.
[3]XU Zhixing,LIU Xiangyong,ZHOU Xiaoqin.A new approach to selective assembly with ant colony algorithm[J].Modern Manufacturing Engineering,2007(9):83-86(in Chinese).[徐知行,刘向勇,周晓勤.基于蚁群算法的选择装配[J].现代制造工程,2007(9):83-86.]
[4]LIU Mingzhou,GUO Jia,LI Qihao,et al.Multi-objective selective assembly of internal-combustion engine linkage of crank-rod based on improved hybrid genetic algorithm[J].Journal of Mechanical Engineering,2006,42(1):155-161(in Chinese).[刘明周,郭 嘉,李旗号,等.基于混合算法的内燃机曲柄连杆机构复合目标选配[J].机械工程学报,2006,42(1):155-161.]
[5]SONG Wenlong,MO Rong,LIU Jiandong,et al.Computer aided selective assembly based on multi-assembly dimension chain[J].Modern Manufacturing Engineering,2007(4):54-56(in Chinese).[宋文龙,莫 蓉,刘建东,等.基于多装配尺寸链的计算机辅助选择装配[J].现代制造工程,2007(4):54-56.]
[6]ZHANG Dong,CHANG Zhiyong,MO Rong,et al.Application particle swarm optimization in computer aided selective assembly[J].Computer Engineering and Applications,2009,45(12):208-211(in Chinese).[张 栋,常智勇,莫 蓉,等.粒子群算法在计算机辅助选择装配中的应用[J].计算机工程与应用,2009,45(12):208-211.]
[7]LIU Jiandong,CHANG Zhiyong,MO Rong,et al.Computer aided selective assembly for multi-dimension chains[J].Computer Integrated Manufacturing Systems,2008,14(5):855-860(in Chinese).[刘建东,常智勇,莫 蓉,等.面向多尺寸链的计算机辅助选择装配模型研究[J].计算机集成制造系统,2008,14(5):855-860.]
[8]HU Jie,WU Zhaotong,YANG Jiangxin.Kinematics model of 3Dtolerance accumulation based on screw parameter[J].China Mechanical Engineering,2003,14(2):127-130(in Chinese).[胡 洁,吴昭同,杨将新.基于旋量参数的三维公差累积的运动学模型[J].中国机械工程,2003,14(2):127-130.]
[9]TAGUCHI G.Quality engineering in Japan[J].Communications in Statistics -Theory and Methods,1985,14(11):2785-2801.
[10]CUI Xunxue,LIN Chuang,FANG Tingjian.A review of the research on multi-objective evolutionary algorithms[J].Pattern Recognition and Artificial Intelligence,2003,16(3):306-314(in Chinese).[崔逊学,林 闯,方廷健.多目标进化算法的研究与进展[J].模式识别与人工智能,2003,16(3):306-314.]
[11]WANG Xiaopeng.Pareto genetic algorithm for multi-objective optimization design[J].System Engineering and Electronics,2003,25(12):1558-1561(in Chinese).[王晓鹏.多目标优化设计中的Pareto遗传算法[J].系统工程与电子技术,2003,25(12):1558-1561.]
[12]PEI Shengyu,ZHOU Yongquan.A multi-objective particle swarm algorithm based on the Pareto optimization solution set[J].Computer Engineering &Science,2010,32(11):85-88(in Chinese).[裴胜玉,周永权.基于Pareto最优解集的多目标粒子群优化算法[J].计算机工程与科学,2010,32(11):85-88.]
- 计算机集成制造系统的其它文章
- 基于模糊物理规划与互反馈的产品工艺方案绿色性分析
- 复杂型腔环切拐角过渡刀轨生成技术

